螺旋軸直徑對螺旋輸送機性能的影響

余書豪，諶永祥

（西南科技大學制造科學與工程學院四川綿陽 621010）

螺旋輸送機的數值模擬方法具有成本低、效率高等特點，便于分析物料顆粒的運動特征。近年來，Shimizu等[1]最早通過離散元方法模擬水平和垂直螺旋輸送機，對不同模型下的力矩、功耗進行了分析。Owen等[2]采用離散元方法預測了螺旋輸送機的性能，討論操作參數對性能的影響。Cleary[3]對物料顆粒的形狀進行研究，分析不同物料顆粒對質量流量、顆粒流態及能量消耗等的影響。孟文俊等[4]對周期邊界條件和全尺寸模型2種計算模型對垂直螺旋輸送機中顆粒流動進行模擬分析。Hou等[5]對團聚顆粒的影響因素進行分析，得出影響顆粒團聚與外界條件的內在關系。張東海[6]研究了變螺距變直徑的螺旋輸送機，并分析了變直徑變螺距輸送機的設計及性能。根據文獻研究發現，螺旋軸直徑的尺寸對螺旋輸送機的影響鮮有研究，而合理的螺旋軸尺寸對輸送機的輸送量和能量消耗等性能指標具有重要的作用。故此采用離散元方法，對不同規格的螺旋軸直徑的螺旋輸送機進行模擬仿真。在不同的螺旋轉速下，比較輸送性能指標的變化，探討螺旋軸直徑對輸送機性能的影響。并采用周期性邊界方法對有限的樣機模型進行分析，有效減少仿真時間，提高仿真效率。

1 離散元方法

1.1 控制方程及其求解

顆粒流中一個顆粒的運動是由移動和轉動2種運動[7-9]合成的結果。顆粒運動中不考慮擾動波傳播對顆粒的影響，可用牛頓第二定律描述單個顆粒的運動。對于單個顆粒，記作i，其控制方程[10]為式（1）和式（2），顆粒之間的相互作用力為式（3）和式（4），顆粒之間的相互作用力矩為式（5）和式（6）。

式中，i，j下標指顆粒 i、顆粒 j；vi為顆粒 i的移動速度，m/s；ωi為顆粒 i的角速度，rad/s；Fn，ij為顆粒 i、j之間的法向接觸力，N，Ft，ij為顆粒 i、j之間的切向接觸力，N，Mt，ij為切向力 Ft，ij產生的力矩，Nmm，Mr，ij為顆粒i、j之間的滾動摩擦力矩，N·mm。

1.2 離散元求解方法

通過計算顆粒之間的相互作用力，對動力學微分方程進行一次積分得到速度關系微分方程，對速度關系微分方程再次求積分，得到顆粒的位置信息。因此，離散元方法是利用經典牛頓第二定律求解各個顆粒在各個運動瞬間的速度、角速度、位移等運動信息。計算模型采用簡化的接觸模型，即Hertz-Mindlin Nonslip接觸模型，這種模型能夠較好地反映真實的顆粒運動狀態。

2 模型及試驗

2.1 驗證模型

為了驗證建立模型的正確性，通過選取與文獻相同的參數和模型，選取螺旋轉速為1 000 r/min，填充系數為30%，時間步長取20%瑞利時步，進行模擬分析，得出顆粒的平均輸送速度和平均輸送流量，表1為不同轉速下平均質量流量的對比分析，表2為不同轉速下顆粒平均速度的對比分析。通過分析可知，質量流量和顆粒平均速度相對于Roberts的實驗數據的平均誤差分別為6.93%和9.43%，誤差存在的原因主要是，由于選取物料顆粒的大小和形狀不同（文獻中采用實際顆粒形狀，本試驗采用球型顆粒）。雖然存在一定的計算偏差，但這個精度足以達到工程應用的要求，驗證了模型建立和參數選取的可行性。

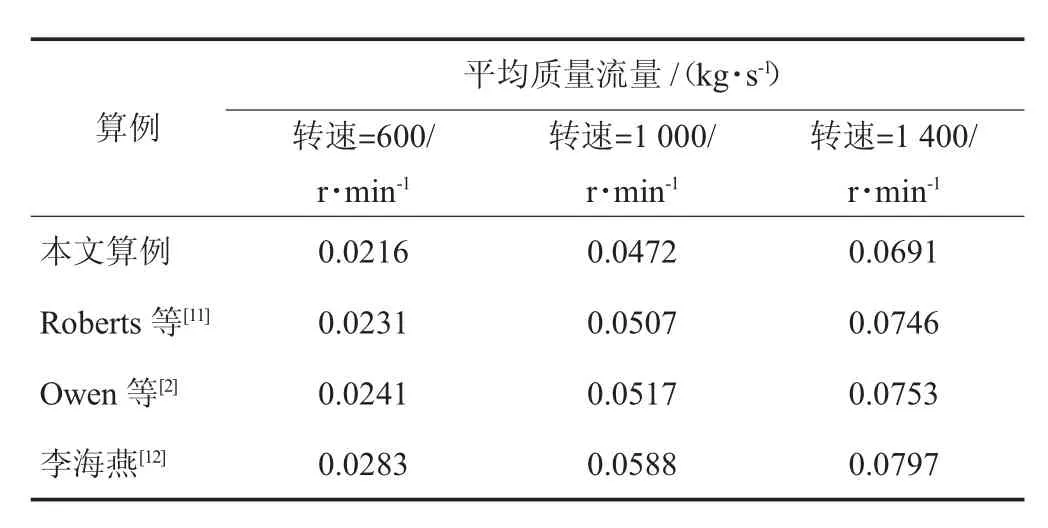
表1 不同轉速下平均質量流量的對比分析Tab.1 Analysis of the mass flow rate under different velocity

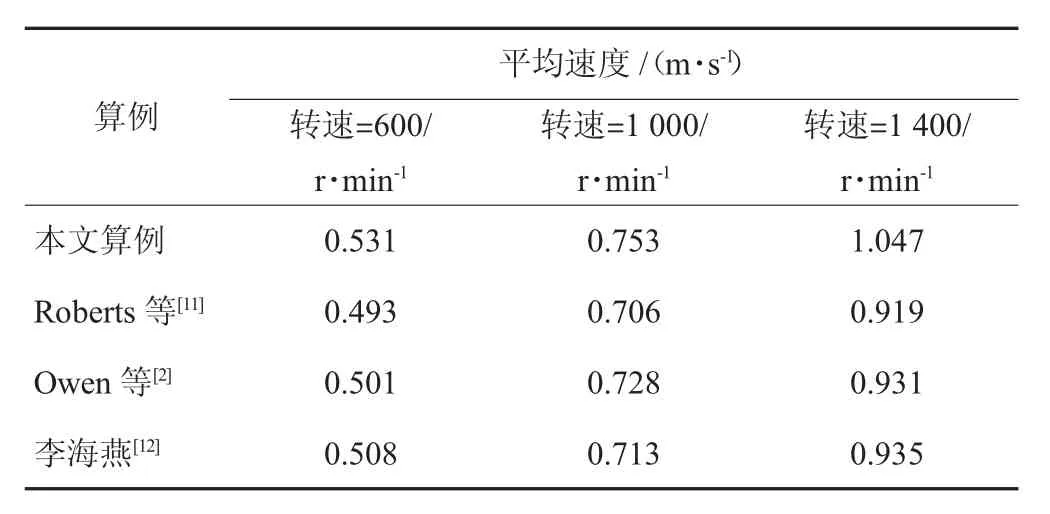
表2 不同轉速下顆粒平均速度的對比分析Tab.2 Analysisoftheaveragevelocityunderdifferentvelocity

2.2 試驗設計

選取3種螺旋轉速600、900、1 200 r/min轉速，螺旋面對應的投影寬度與螺旋軸直徑如表3所示，螺旋面投影寬度是指螺旋面橫截面的投影彎度。因此，根據排列組合知識，共需進行試驗15次。為了表示的方便，A、B 和 C 分別表示轉速 600、900、1 200 r/min。例如模型號1與A組成的試驗記為A1；同理，A2、A3。對于B、C采用同種記法。

表3 不同模型下的螺旋面投影寬度與螺旋軸直徑Tab.3 Projection width of spiral surface and screw shaft diameter in different models

2.3 模型參數的描述

考慮到減少計算時間，需要利用合適的樣機模型和簡便的處理方法。為了便于參數數據與參考文獻進行對照，采用底部供料的螺旋輸送機，其模型參數：螺旋葉片外徑為38 mm，機筒的外徑為40 mm，葉片與筒壁間隙為0.5 mm，機筒壁厚為0.5 mm，螺旋軸直徑按照試驗組數據獲取，螺距為38 mm，螺旋葉片厚為1 mm，螺旋長度為114 mm，螺旋頭數為1。為了在有限的結構空間模擬實際中大型樣機的效果，將螺旋筒壁的上、下端部開口，并設為周期性邊界，即物料到達上部顆粒后，通過底部以相同的速度再次進入輸送機，以接近實際的輸送工況。

通過三維軟件Autodesk Inventor 2015建立三維模型，并以通用的CAD文件格式將其導入EDEM軟件中，需要注意的是，Autodesk Inventor 2015可以滿足參數建模的需求，因此對試驗組中不同的螺旋體通過其參數化建模，可以很方便地得到相應尺寸下的虛擬樣機模型。圖1、2分別為螺旋輸送機的示意圖和三維模型圖。

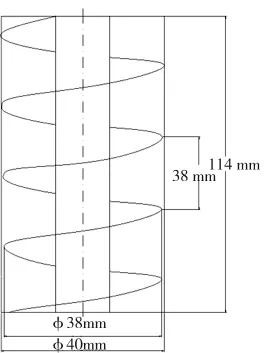
圖1 螺旋輸送機示意圖Fig.1 Diagram of screw conveyor

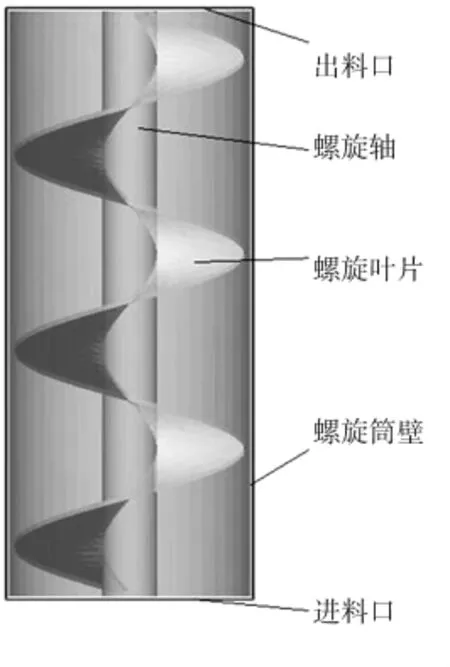
圖2 螺旋輸送機三維模型Fig.2 Three dimensional model of screw conveyor

3 結果的求解及分析

3.1 EDEM軟件求解

當導入三維模型至離散元[13]軟件EDEM后，需要設置模擬的邊界條件：對輸送機的螺旋軸、螺旋葉片和筒壁設為幾何體類型，對顆粒盤設為虛擬壁面條件。入口的顆粒粒徑分布為正態分布，顆粒平均半徑是1 mm，標準差是0.05，顆粒產生的位置是在顆粒盤上隨機的，顆粒產生的速率是每秒5 000個，螺旋葉片的轉速按照試驗設計的工況進行。由于EDEM求解效率與仿真區域的大小直接相關，因此為了使網格單元數小于105個，通過不斷嘗試，在保證單元大小是2倍的顆粒平均半徑基礎上，最終確定對輸送機劃分為22 000個網格單元，以保證求解的可行性和準確性。時間步長為20%時間步長，最大嘗試放置顆粒的次數為20，顆粒盤設置在進料口對應的橫截面，大小26.4 mm×26.4 mm。

3.2 結果分析

3.2.1 運動分析

由于試驗組分組數較多，選取具有代表性的2種操作參數進行分析，即相同轉速下不同的螺旋軸尺寸和相同的螺旋軸尺寸下不同的螺旋轉速。分別選取試驗組A1—A5和試驗組A3、B3、C3進行分析。圖3為不同螺旋軸直徑對應的輸送顆粒分布。

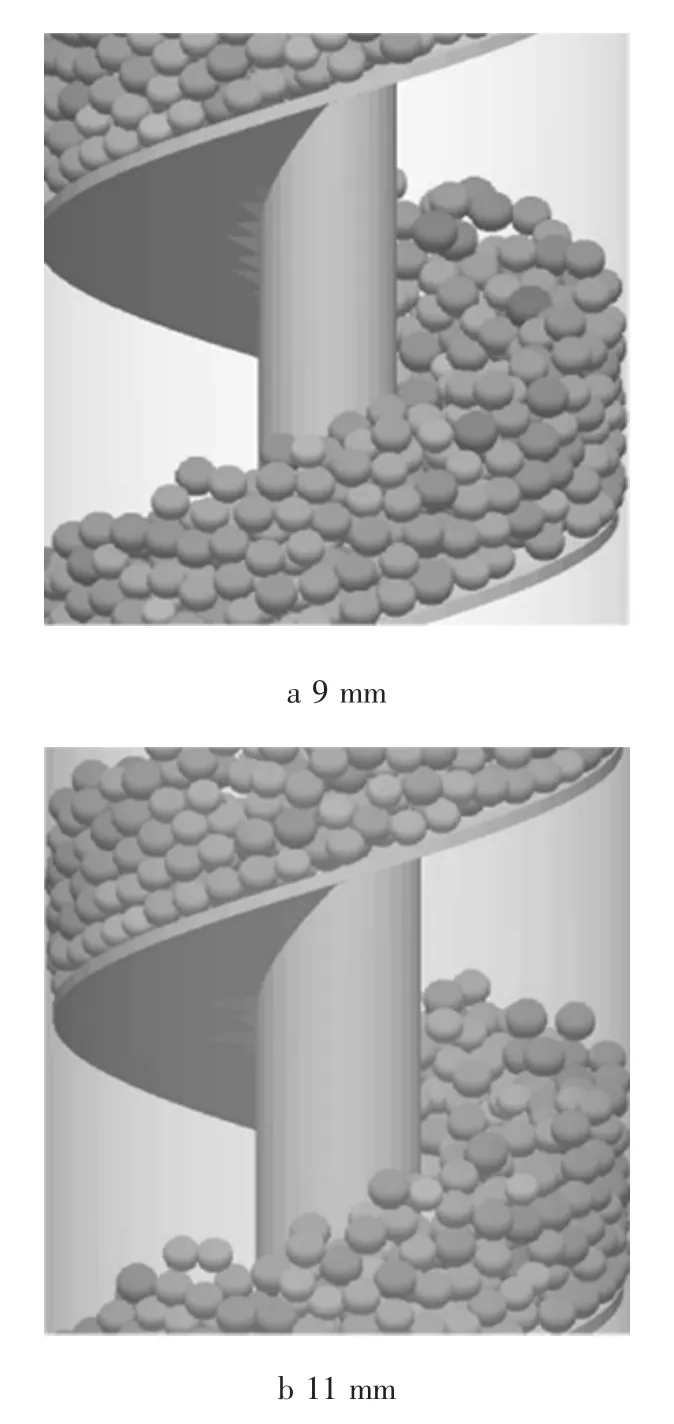
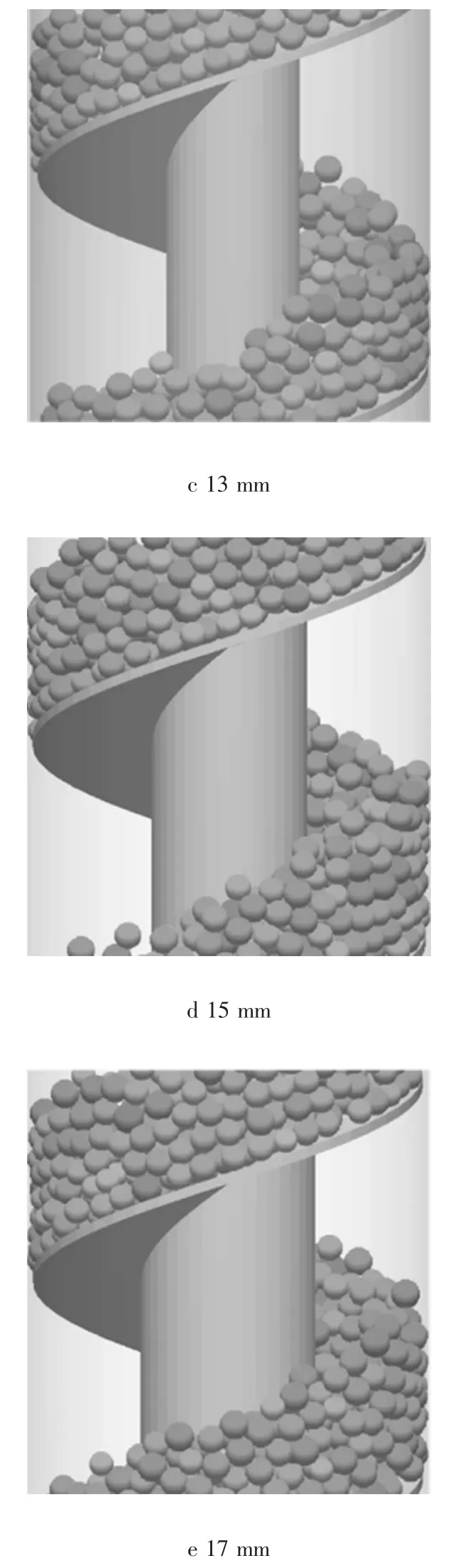
圖3 不同螺旋軸直徑對應的輸送顆粒分布Fig.3 Particles of conveying of different screw shaft sizes

在螺旋轉速為600 r/min，進口速度3 m/s下不同螺旋軸尺寸對應的輸送機顆粒運動[14]仿真情況。顆粒按顆粒的平均尺寸大小進行著色，小顆粒對應淺灰色，大顆粒對應深灰色，中間顆粒尺寸對應灰色。由圖3a—e可知，隨著螺旋軸尺寸的增加，顆粒的平均質量流量變化不大，說明顆粒在單位體積上的顆粒數增加，這可以從圖3d、e中看出，顆粒的堆積層深度明顯增加。從顆粒分布的均勻性角度分析，圖3c顆粒的分析比較均勻，有大顆粒分布在圓周的外層，小顆粒分布內層，中間顆粒分布在兩者之間的空間內。

圖4為不同螺旋轉速對應的輸送顆粒分布。在螺旋軸直徑為13 mm下，不同螺旋轉速對應的螺旋輸送機的運動顆粒仿真情況。

圖4 不同螺旋轉速對應的輸送顆粒分布Fig.4 Particles of conveying of different rotational velocities

顆粒按照其速度的大小進行著色，速度較大的顆粒對應深灰色，速度較小的顆粒對應淺灰色，中間速度的顆粒對應灰色。由圖4a、b、c可知，隨著螺旋轉速的增加，顆粒的運動穩定性發生了變化。從螺旋轉速600 r/min增大至900 r/min，發現顆粒運動更加穩定，速度分布相對均勻，只有個別顆粒的運動遠離流化層；當螺旋轉速繼續增大至1 200 r/min時，發現顆粒的運動穩定性明顯降低，有明顯一部分顆粒在靠近螺旋筒壁附近運動，顆粒與螺旋體之間的相對運動明顯加劇，導致相對螺旋體顆粒運動不規律，且速度穩定性被打破。

3.2.2 性能指標分析

通過對仿真結果進行分析，得出反映輸送機性能的指標：顆粒平均輸送速度、能量消耗、平均質量流量和法向接觸力的大小，揭示螺旋軸的直徑對輸送機性能的影響，表4為各試驗組對應的性能指標。

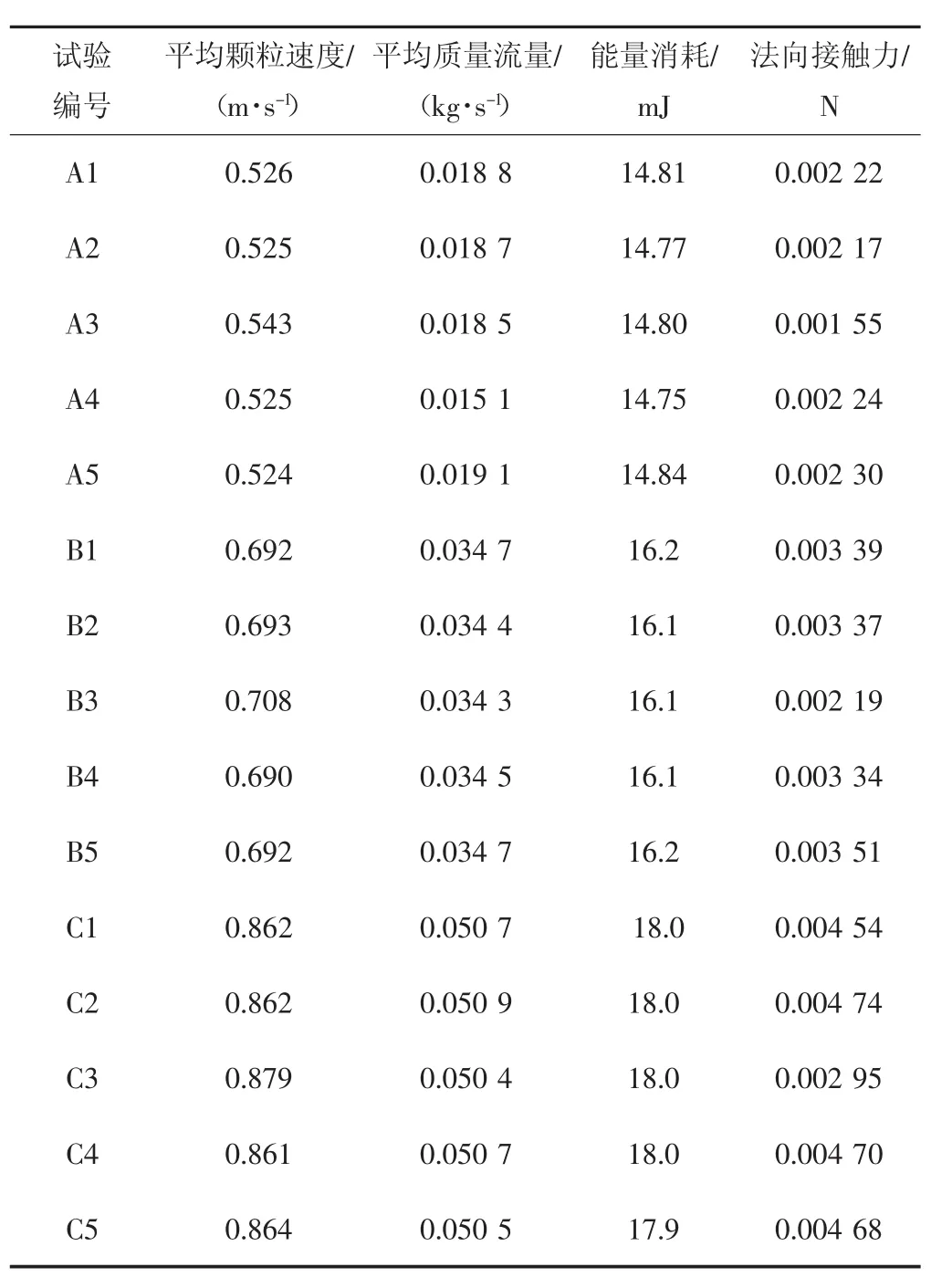
表4 各試驗組對應的性能指標Tab.4 Values of performance indexes in the different experiment group

顆粒的平均輸送速度采用穩態后的時間段內平均速度；能量消耗采用穩態后時間段內的平均能量消耗；平均質量流量采用軟件后處理工具中質量流量傳感器獲取。選取圓筒型，半徑為20 mm，50條邊，選取穩定輸送區段，即距離低端進料口上方30 mm處為觀測圓筒形底面，圓筒的高度是40 mm。通過試驗，發現質量流量傳感器的放置是合理的。對于法向接觸力[15]，只考慮顆粒之間的平均接觸力。

圖5為不同螺旋軸直徑下顆粒平均速度和質量流量，圖6為不同螺旋軸直徑下的能量消耗和法向接觸力。在螺旋轉速為600 r/min，進口速度為3 m/s時，對應性能指標在不同螺旋軸直徑下的變化趨勢。相同轉速下，試驗組A3的顆粒平均速度最大，試驗組A1、A5對應的平均質量流量較大；對于能量消耗，各試驗組的差別較小；對于法向接觸力，試驗A3最小，說明顆粒的分布比較均勻，相互之間的平均作用力較小，即形成了一定程度地流化床。

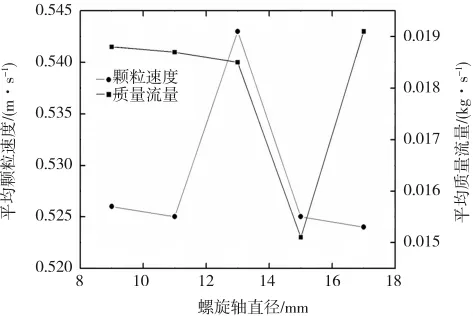
圖5 不同螺旋軸直徑下的顆粒平均速度和質量流量Fig.5 Average particle velocity and Average mass flow rate in different diameters of screw shaft

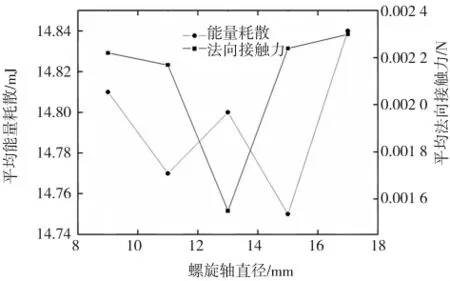
圖6 不同螺旋軸直徑下的能量消耗和法向接觸力Fig.6 Average energy dissipation and average normal force in different diameters of screw shaft

綜上分析，試驗組A3、B3、C3對應的顆粒平均速度較大，能量消耗適中，且顆粒之間的法向作用力最小。同時，從試驗組A3、B3、C3對應的數據可知，隨著螺旋轉速的增加，顆粒的平均速度增大，平均質量流量增大，對應的能量消耗增大，顆粒之間的法向接觸力增大，顆粒之間運動的穩定性較低。因此，在保證一定的輸送量的同時，螺旋轉速的取值不宜過大，這對于顆粒整體輸送的穩定性和能量利用率都能夠得到顯著提高。

4 結論

采用顆粒物質力學方法，借助離散元分析軟件，分析螺旋軸直徑對螺旋輸送機性能的影響，得出如下結論：

1）分析了離散元求解方法，對樣機模型進行了驗證，得出的性能參數數據與文獻中實驗數據吻合性較好。

2）隨著螺旋轉速的增加，相同螺旋軸對應的顆粒平均速度增大、能量消耗增加、法向接觸力增加，顆粒輸送的穩定性降低；在相同的螺旋轉速下，隨著螺旋軸直徑的增加，顆粒在單位體積上的顆粒數增加，流化層深度增加。

3）在保證輸送量的同時，實驗選出適合的螺旋轉速為900 r/min，螺旋軸直徑為13 mm為較好的一組參數。

參考文獻（References）：

[1]SHIMIZU Y，CUNDALL P A，Three-dimensional DEM simulation of bulk handling screw conveyors[J].Journal of Engineering Mechanics，2001，127（9）:864-672.

[2]OWEN P J，CLEARY P W，Prediction of screw conveyor performance using the Discrete Element Method（DEM）[J].Powder Technology，2009，193（3）:274-288.

[3]CLEARY P W.DEM modeling of particulate flow in a screw feeder[J].Progress in Computational Fluid Dynamics，2007，7:128-138.

[4]孟文俊，王曉竑，垂直螺旋輸送機內物料的運動密度研究 [J].硫磷設計與粉體工程，2009（3）：24-27.

[5]HOU Q F，DONG K J，YU A B.DEM study of the cohesive particles in a screw feeder[J].Powder Technology，2014，256:529-539.

[6]張東海.螺旋輸送機的優化研究[D].大連：大連理工大學，2006.

[7]蘆新春，孔慧敏.基于iSIGHT的螺旋輸送機6σ質量優化設計[J].中國農機化學報，2015，36（1），67-70.

[8]魏群.垂直螺旋輸送過程中物料動力學分析 [J].能源技術與管理，2016，41（1）：14-16.

[9]史嵩，張東興，楊麗，等.基于EDEM軟件的氣壓組合孔式排種器充種性能模擬與驗證[J].農業工程學報，2015，31（3），62-69.

[10]CHEN H，LIU Y L，ZHAO X.Q.，et al.Numerical investigation on angle of repose and force network from granular pile in variable gravitational environments[J].Power Technology，2015，283:607-617.

[11]ROBERTS A W，WILLIS A H.Performance of grain augers[J].Proceedings of the institution of Mechanical Engineers，1962，176（8）:165-194.

[12]李海燕.基于EDEM的垂直螺旋輸送機性能參數仿真研究[D].太原：太原科技大學，2011.

[13]胡國明.顆粒系統的離散元素法分析仿真[M].武漢：武漢理工大學出版社，2010:110-135.

[14]趙占一，孟文俊，孫曉霞，等.垂直螺旋輸送機中顆粒速度的分布[J].過程工程學報，2015，15（6）:909-915.

[15]陳慶為，黃國慶.螺旋取料裝置內螺旋聯接軸承結構形式分析[J].港口裝卸，2014（1）:21-22.