核電站放射性廢物超壓機壓餅裝載優化研究

于 博 汪再恒 林川渝 韓孝東 王展鵬

(1. 中電投山東核環保有限公司, 山東 煙臺, 265116； 2. 山東核電有限公司, 山東 煙臺, 265116)

某AP1000核電站預計單臺機組每年產生134 m3可壓縮放射性廢物(放射性廢物處理設施簡圖示于圖1)，這部分廢物裝入200 L鋼桶中轉運至固廢分揀和壓縮系統的輥道上，先經過實時射線成像裝置(RTR)檢測其中是否有不適合超壓或在人工分揀和預壓期間可能對人有危害的任何廢物，如有則轉運至分揀手套箱進行分揀。RTR檢測合格的廢物桶經預壓機進行預壓，以實現初步減容(減容比約為3)，預壓完畢的200 L桶送到高分辨率γ譜儀(HRGS)進行核素分析，后由輥道輸送至超壓站進行超壓，壓餅在優選臺上進行優選后裝入320 L鋼桶，裝桶完畢后送到灌漿站進行灌漿，經過振動臺振實，對320 L廢物桶加蓋，經過一段時間的養護后，測量廢物桶表面劑量率和表面污染，使用數控吊車送入320 L桶暫存庫暫存。

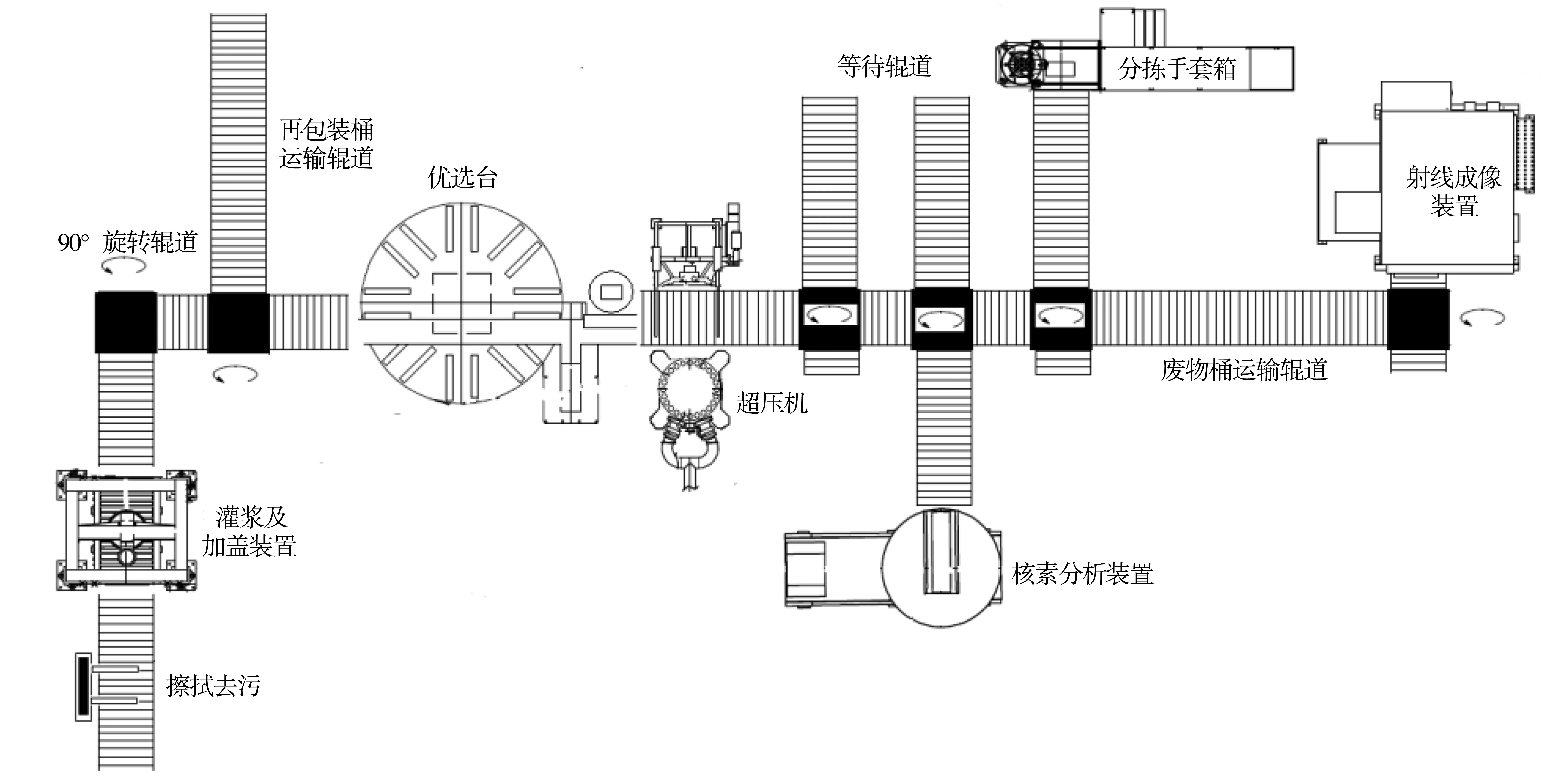
圖1 某核電站放射性廢物處理設施布置簡圖

超壓裝置壓餅時壓力為1 500 t，綜合減容比為4.5，每小時可壓縮10個廢物桶。優選臺共設置8個壓餅暫存位置，抓具按照壓餅生產時間先后依次抓取壓餅，放入再包裝桶中，同時計算再包裝桶剩余高度，確定下一個壓餅能否放入。如果能，則放入；如果不能，則放入第二個再包裝桶中。重復上述步驟，直至所有壓餅都被放入再包裝桶中。

廢物裝桶過程中，操作人員會根據廢物的活度水平及廢物類型進行組合裝桶，確保單個壓餅的放射性不會過高，且壓縮比為3～5。本文僅從提高壓餅裝載率的角度進行研究，尋找能使再包裝桶實現最大裝載率的方案，故假設壓餅裝載過程為簡單的一維裝箱問題。

1 經典一維裝箱問題

1.1 經典一維裝箱問題的數學描述

有n件物品a1，a2，…，an，要裝入到若干個單位容積的箱子中，可用的箱子為B1，B2，…，Bm，要求每一件物品aj只能裝入到一個箱子里，每一個箱子中的數字和不超過1，如何用最少的單位容積的箱子，裝下所有的物品。

用線性規劃的方式來描述這個問題：

式中，a1、a2、an為第1、第2、第n件物品，n為物品數量；B1、B2、Bm為第1、第2、第m個箱子，m為箱子的數量；z為所使用箱子數之和；i為箱子序號，1≤i≤m；j為物品序號，1≤j≤n；vj為第j件物品尺寸。

1.2 經典的一維算法

由于裝箱問題是一個典型的NP hard問題，到目前為止尚未找到此類問題的多項式時間解法[1]。很多學者在二十世紀七八十年代就提出了解決裝箱問題的各種近似算法，根據貨物裝箱過程的特點，按照貨物的到達情況進行分類，可分為在線裝箱和離線裝箱。

(1) 在線算法

如果一個近似裝箱算法在執行過程中，每當一個物品到達時，就立刻決定把該物品放入哪個箱子中，而不管后序物品如何，這種算法就被稱為在線算法[2]，主要有下次適應算法、首次適應算法、最佳適應算法等。

(2) 離線算法

如果算法在開始裝箱之前，就已經得到了所有物品的信息而一次性確定裝箱策略，這種算法就被稱為離線算法[2]。離線算法主要有降序首次適應算法和降序最佳適應算法等。

由于本文涉及到最佳適應算法及降序最佳適應算法，故對這兩種算法進行詳細說明。

最佳適應算法[3]：按順序依次處理各物品，首先把物品a1放入箱子B1中，再考慮物品a2，如果a2能夠放B1中則將其放入，否則打開一個新的箱子B2，并將a2放入B2中。按照相同的方法依次序處理各物品，在處理物品aj時，假設已使用的箱子是B1，B2，，…，Bi，將物品aj放到所有能夠放下aj且剩余高度最小的箱子中，只有當所有己使用的箱子都不能放下物品aj時，才打開一個新的箱子，并把物品aj放入這個箱子中。

降序最佳適應算法[4]：首先將所有物品根據其尺寸大小按遞減順序排序，假設排序后的物品為a1，a2，…，an，物品aj的尺寸為vj，且v1≥v2≥…≥vn，然后再按照最佳適應算法進行裝箱。

算法的時間復雜度和平均性能比是評測近似算法性能的兩個重要標準，表1中列出了部分著名裝箱問題近似算法的研究現狀[2]。

表1 經典一維裝箱問題的幾種著名近似算法

1) O(n)代表物品量增大n倍時耗時增大n倍；

2) O(n×lgn)代表物品量增大n倍時耗時增大n×lgn倍。

由表1可以看出，最佳適應算法與降序最佳適應算法在時間復雜度和平均性能比上的表現是一樣的。

2 壓餅裝載優化研究

2.1 采用在用方案進行裝載

某AP1000核電機組目前在用裝載方案采用最佳適應算法進行計算，其裝載流程示于圖2。

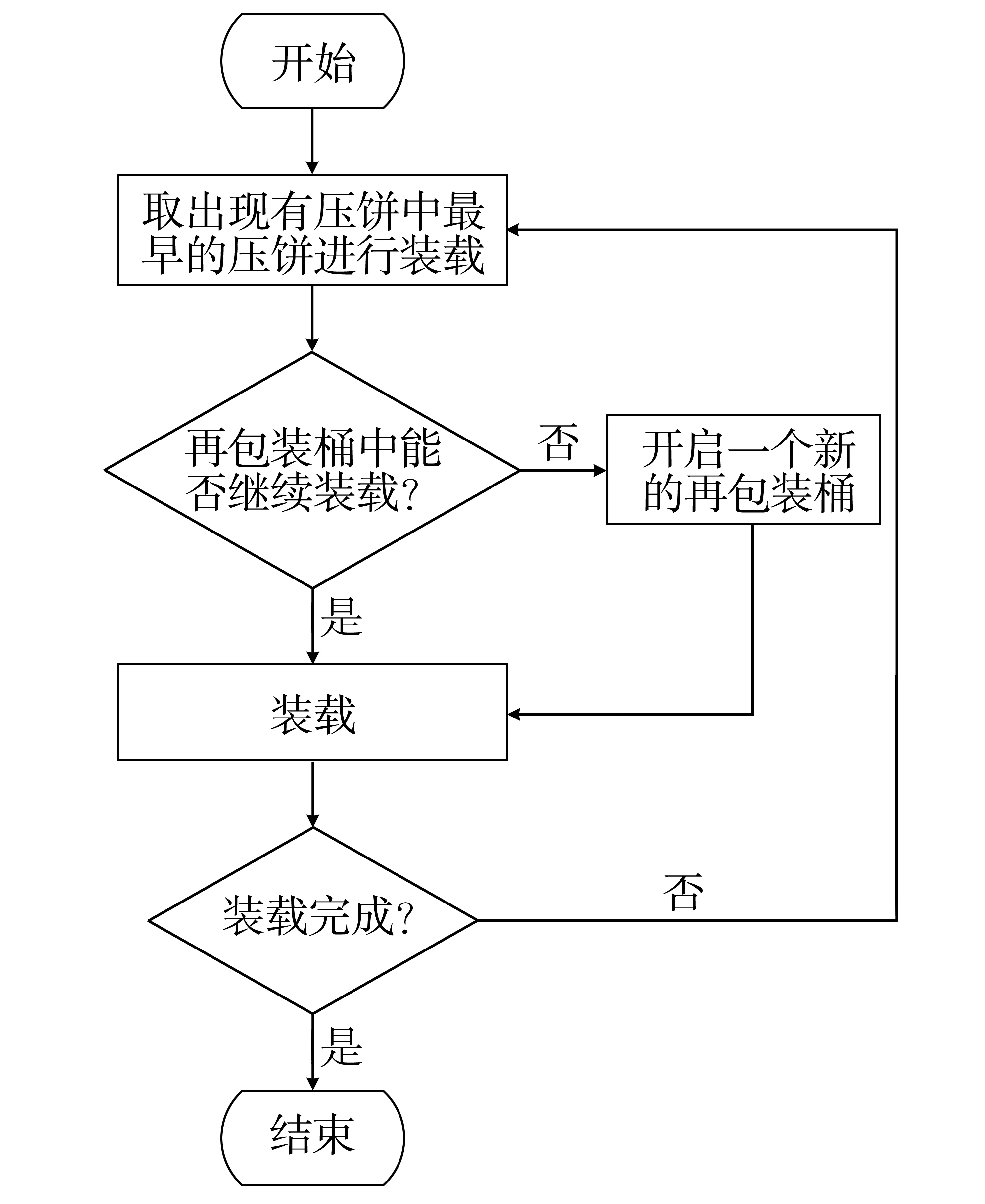
圖2某AP1000機組在用壓餅裝載方案裝載流程

由以往實驗數據中隨機抽取45個壓餅(參數列于表2)。

由表2可見，該電站的超壓機綜合壓縮比分布為3～5，壓餅最終高度為180～250 mm。原因是在裝載過程中采用組合裝載的方式，最終壓餅的高度分布比較集中。

壓餅直徑為610 mm，320 L桶有效內徑為650 mm，由于320 L桶內壁安裝了防反彈裝置，可以保證壓餅在320 L桶內不會因為偏心導致漂浮的情況出現。之所以選擇45個壓餅信息進行裝載，是考慮到后面改進方案中需要考慮45個壓餅一起裝載的情況。

采用在用裝載方案對表2中壓餅進行模擬裝載，其裝載結果列于表3。

由表3可知，采用在用裝載方案，裝載45個壓餅共需15個320 L的再包裝桶，平均裝載率為80%，每個桶的裝載率均未達到90%。其中，裝載率最高的11號和14號再包裝桶也僅為89%。

裝載率低會導致后續灌漿程中容易出現壓餅漂浮的問題，雖然設置了抗漂浮裝置，但只有當再包裝桶裝載率高于80%時，抗漂浮效果才最好。同時，裝載率低，也意味著灌漿過程中廢物增容比增加，不利于廢物最小化總體目標的實現。因此，有必要對在用裝載方式進行優化。

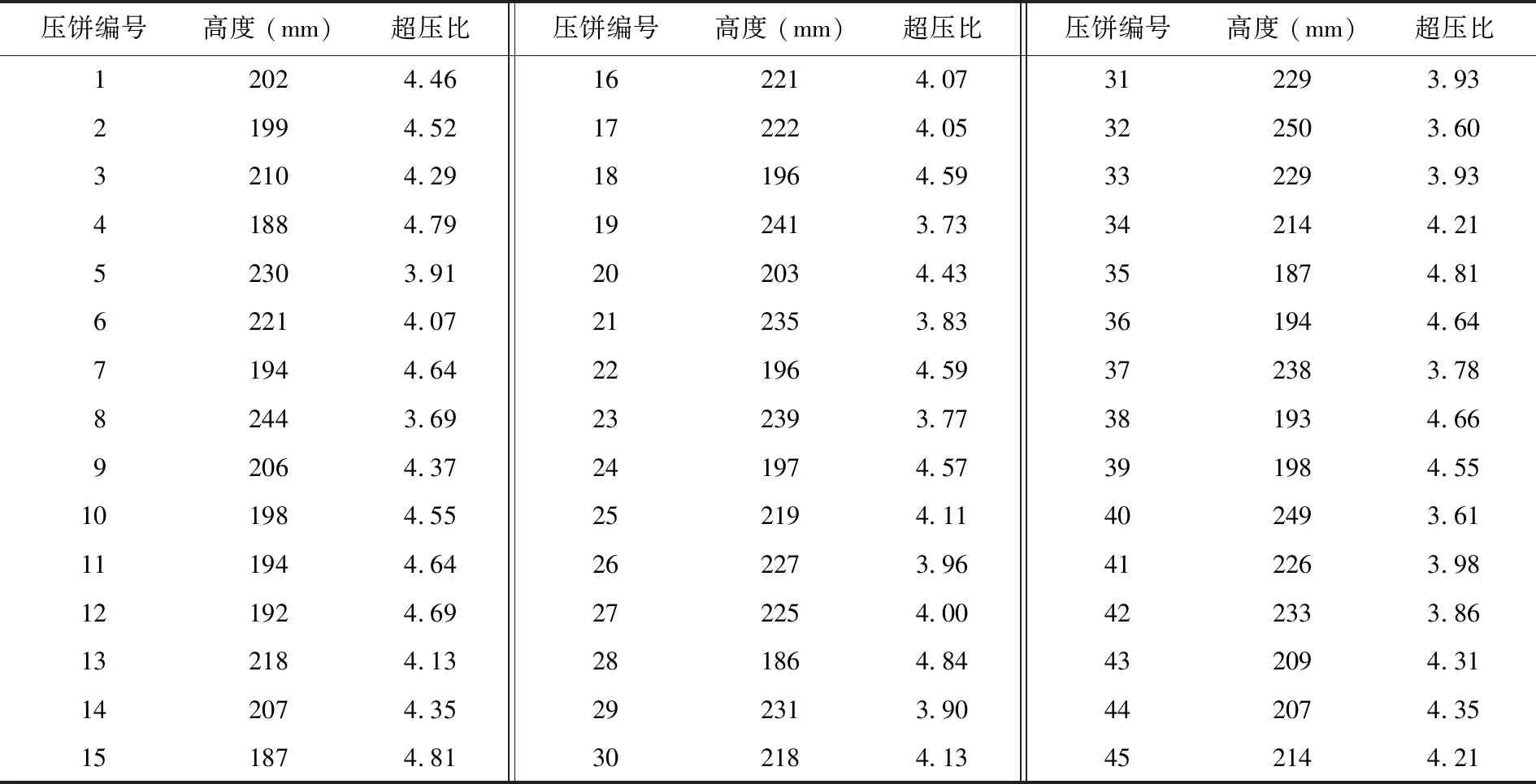
表2 壓餅信息

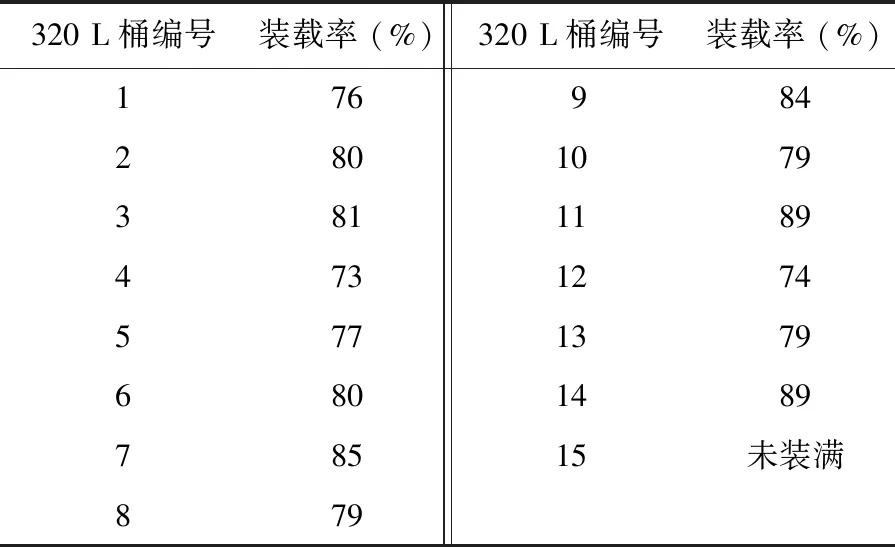
表3 在用方案的裝載結果

2.2 采用優化方案進行裝載

本文先對壓餅進行優選，再結合降序最佳適應算法進行裝載優化，其表達如下：

在所有壓餅組合中，尋找組合a1，a2，…，at，t為小于等于4的正整數，壓餅aj(1≤j≤t)高度為hj，使其滿足以下條件：

(2) 當有不止一個組合滿足條件(1)時，選擇其中裝載率最大的組合。

(3) 當裝載率最大的組合有不止一個時，選擇其中壓餅時間最早的一個組合。

(4)當不能選出符合條件的組合時，按照降序最佳適應算法進行裝載。

重復以上動作，直至所有壓餅都被裝入再包裝桶內為止，裝載流程如圖3所示。

優化方案采用離線算法，即需要先積攢一定數量的壓餅后再進行裝載，取消目前的超壓機優選臺，在該區域設置壓餅暫存單元，可一次性暫存約45個壓餅，如圖4所示。

單臺機組每年產生134 m3可壓縮廢物，經預壓減容(減容比約為3)后廢物量約為45 m3。按照200 L桶裝滿廢物估算，每年至少產生壓餅225個。考慮到可壓縮廢物主要來源于大修期間，若對大修期間廢物集中進行超壓，完全可實現一次性裝載45個壓餅。

按照圖4所示的布置，為了方便吊車操作，應首先考慮將壓餅裝滿一行或一列，根據以往經驗，每個再包裝桶大約可以裝載3～4個壓餅，9個壓餅基本可以滿足兩個再包裝桶的裝載。

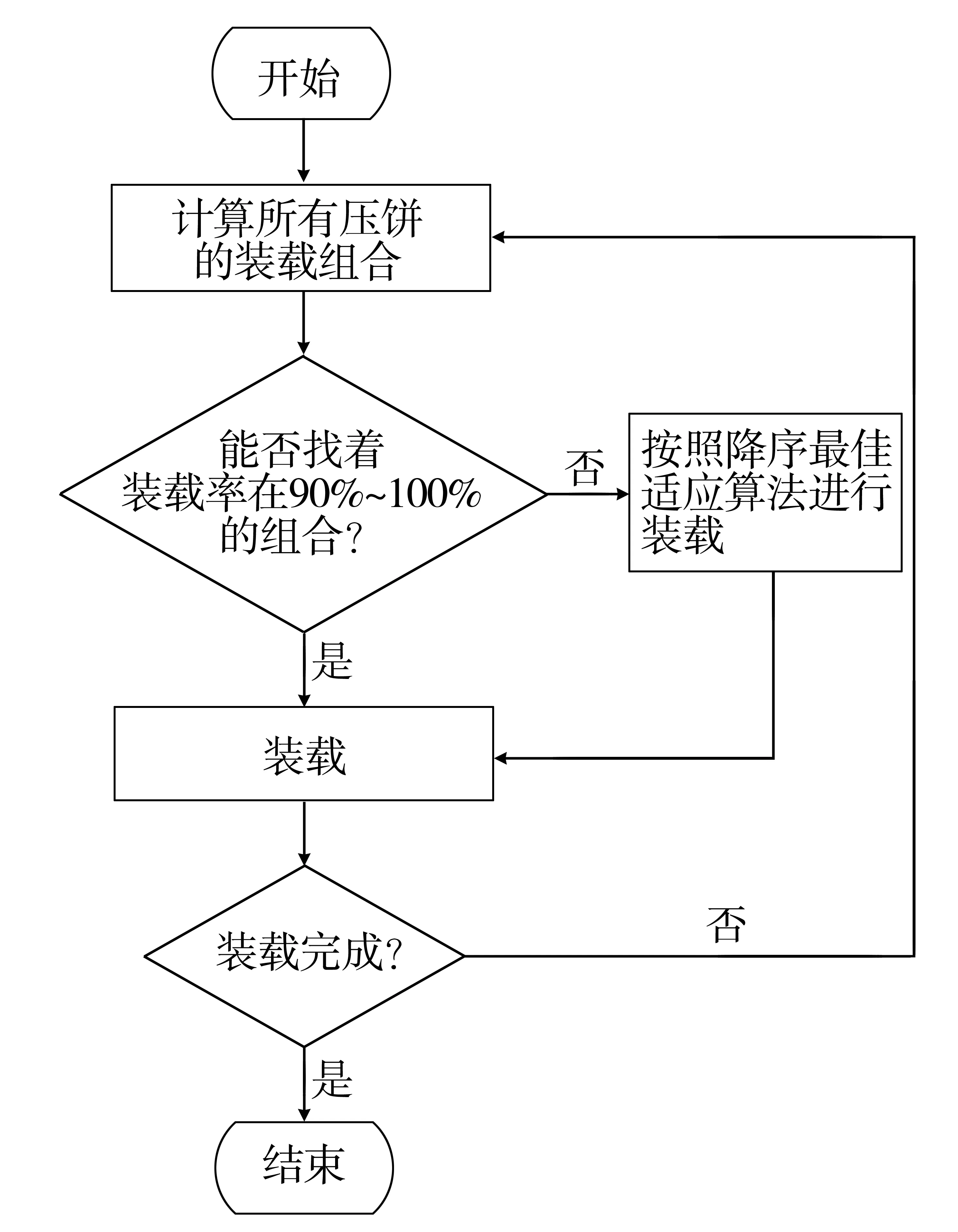
圖3 優化方案裝載流程圖

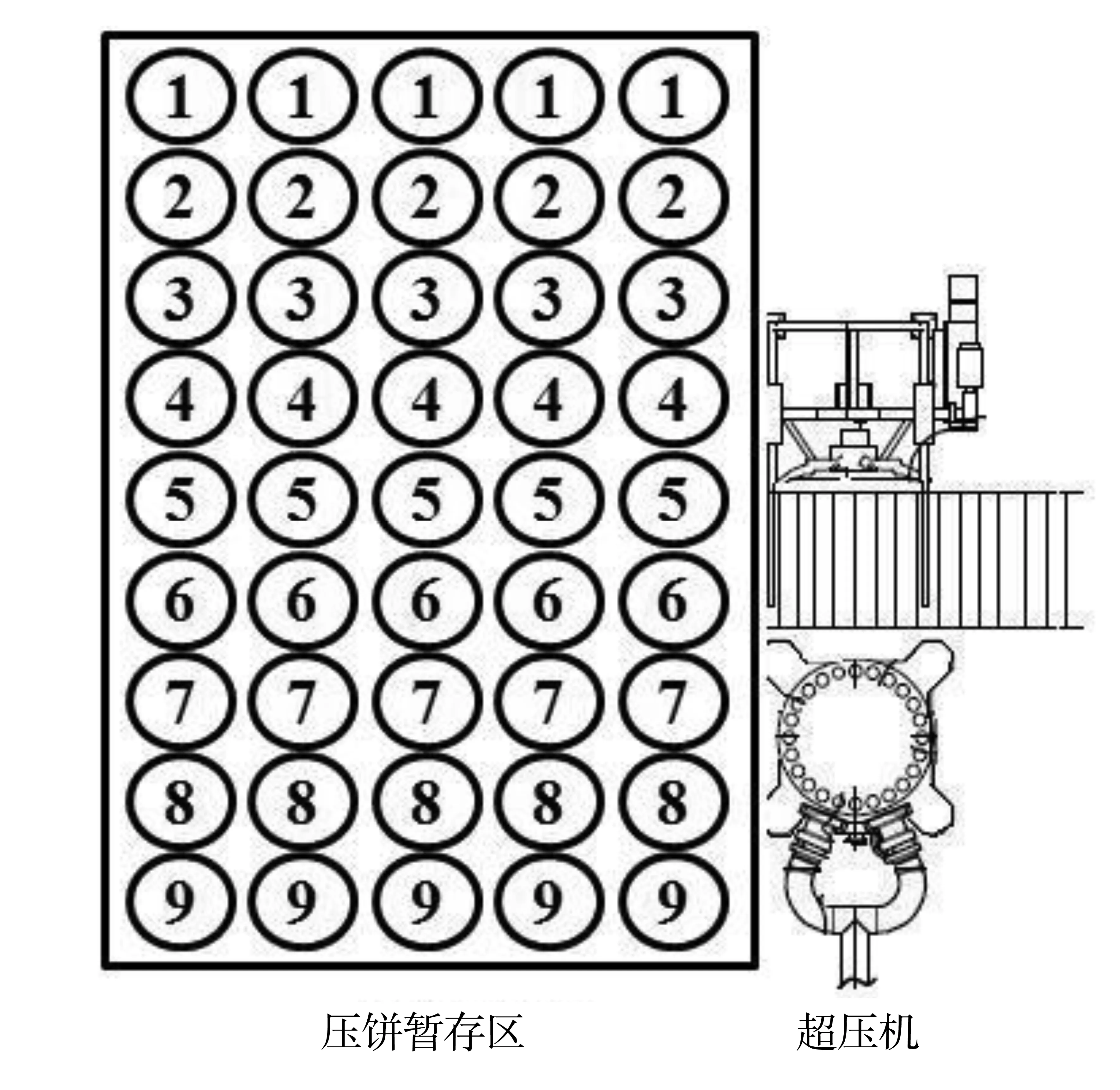
圖4 壓餅暫存區示意圖

仍以表2中的一組數據為例，分別考慮裝滿1列壓餅、2列壓餅、3列壓餅、4列和5列壓餅后再進行統一裝載的情況，同時增加12個一組和15個一組的情況作為對比，采用規劃求解的方法進行模擬裝載，其裝載結果列于表4。

由表4可知，采用優化方案進行裝載，無論如何分組，其平均裝載率都明顯高于在用方案，且單個桶的裝載率除個別外基本都在80%以上。壓餅組合為12、15、18、27、36個時，平均裝載率差別不大，均可達到90%左右，高于9個一組的情況；當一次裝載45個壓餅時，平均裝載率有明顯提高，可達92.46%。就單桶的裝載率而言，壓餅組合數越多，出現裝載率達90%的概率就越大，甚至會出現裝載率為100%的情況。總的來說，一次性裝載的壓餅數越多，裝載率越大。

3 結果分析

單臺機組每年產生壓餅數量約為225 個，采用不同方式進行裝載，年產生廢物量列于表5。

與在用裝載方案比，優化方案中，一次性裝載9、12、15、18、27、36 個壓餅的情況下，單臺機組每年產生的廢物量可減少2.88 m3；一次性裝載45個壓餅，單臺機組每年產生的廢物量可減少3.2 m3。優化方案的平均裝載率均明顯高于在用方案，其中一次性裝載45個壓餅時，與在用裝載方案相比，廢物量減少約13%。

在用方案采用在線裝載，按照壓餅生產時間先后順序進行裝載，不需要設置專門的壓餅暫存區，也不用考慮因壓餅長時間存放帶來的放射性，其缺點是無法實現再包裝桶的最大化裝載，導致在后續灌漿過程中容易出現漂浮問題，同時邊壓邊裝載會導致裝載效率下降，不能充分發揮超壓機的高效率的優點。按照在用方案裝載，每天能處理18個壓餅。

優化后采用離線裝載，采用優化方案裝載，需要在裝載區域設置專門的壓餅暫存區，若壓餅數量較多或需要長時間暫存，還需考慮壓餅屏蔽問題。也可將廢物集中處理，根據廢物量選擇壓餅組合方式進行一次性裝載，避免壓餅長時間存放。采用優化方案，預計一天可處理45個壓餅。

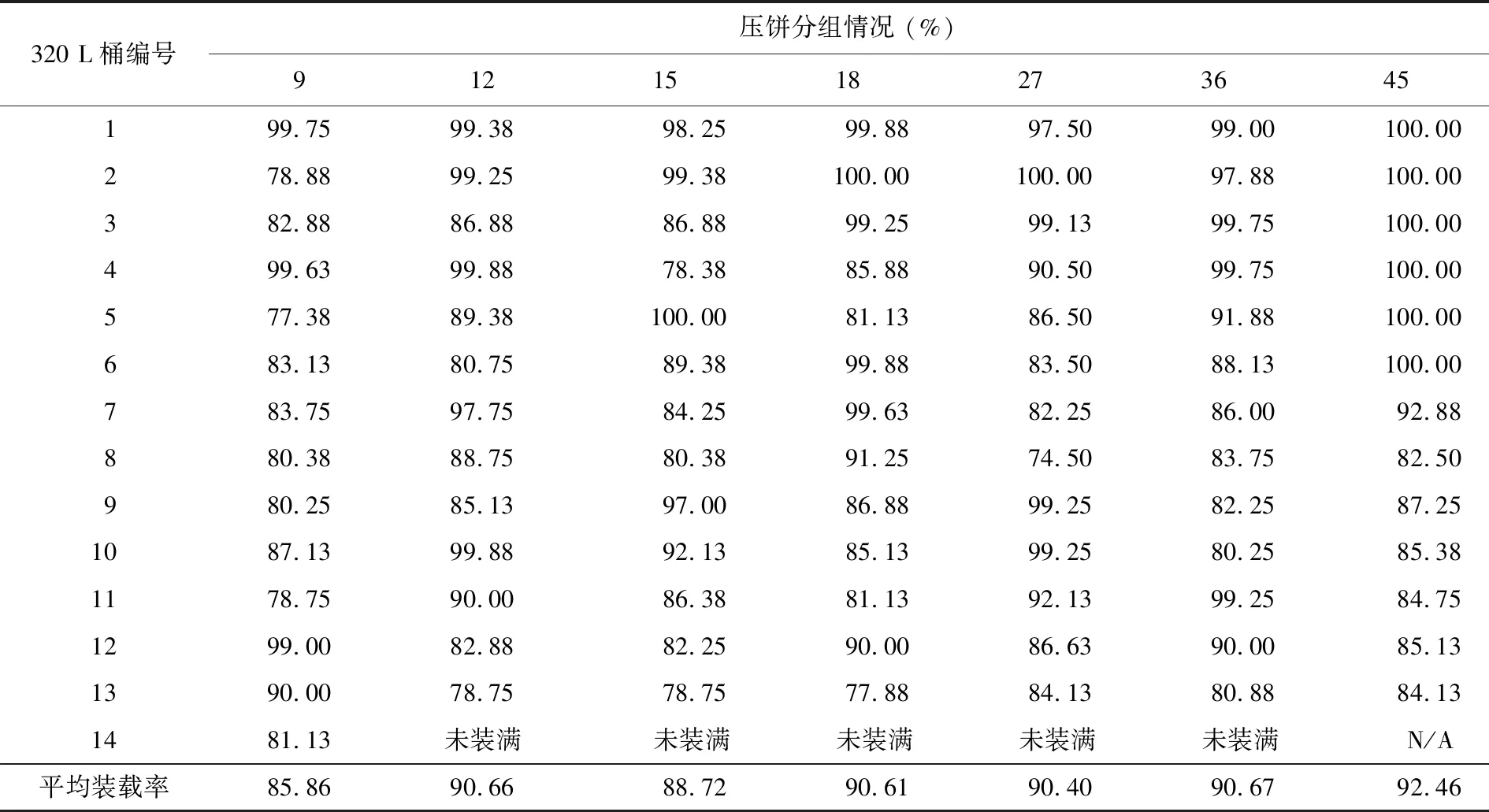
表4 不同分組情況下的裝載結果

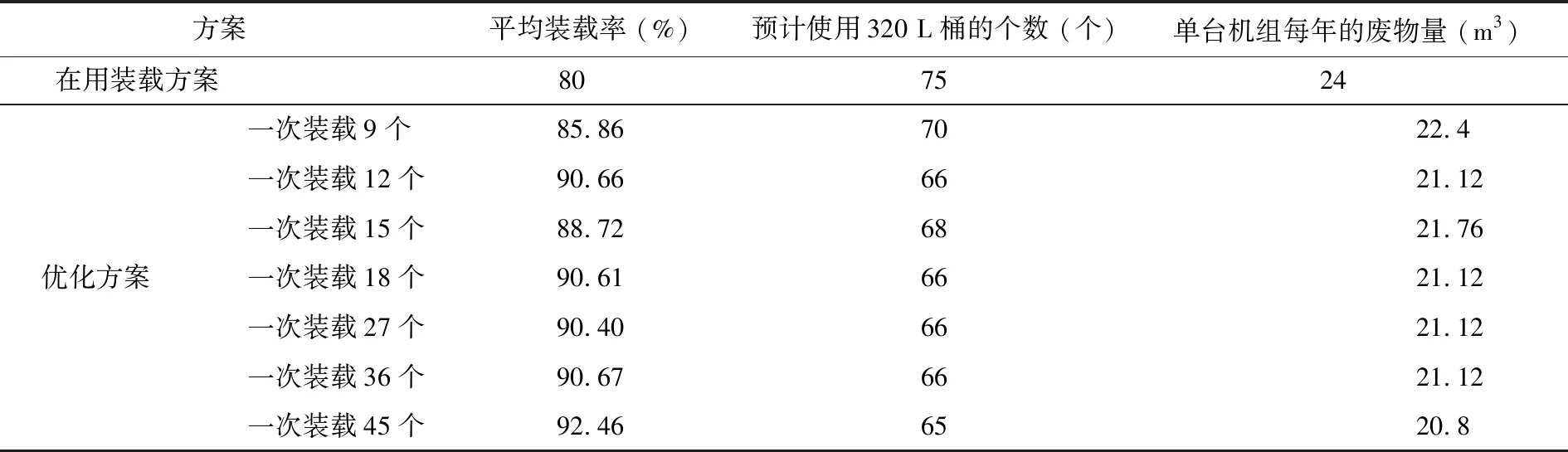
表5 不同裝載方案的最終廢物量預計

4 結語

針對核電站放射性廢物超壓機壓餅在用裝載方案中再包裝桶裝載率低、壓餅處理效率低、灌漿過程中易出現漂浮等問題，提出了優化改進方案，選取以往數據進行了模擬裝載運算，證明了優化方案能顯著提高再包裝桶裝載率。同時，優化方案可以根據廢物數量選擇合理組合進行裝載，提高了廢物裝載率及處理效率，避免了后續灌漿過程中壓餅漂浮的問題，以及減少最終處置廢物量。

該方案目前雖未實施，但對核電站放射性廢物處理具有實際意義，建議盡早實施。