GOMP改進算法在信道估計中的應用

任曉奎　張芷寧

(遼寧工程技術大學電子與信息工程學院　遼寧 葫蘆島 125105)

0　引　言

在信號或者圖像的處理、傳輸等方面，奈奎斯特采樣定律一直都是遵循的準則，但由于其在資源利用率等的方面的缺陷促進了壓縮感知CS(Compressed sensing)這一新采樣技術的出現。相比于奈奎斯特采樣定律，壓縮感知技術是將壓縮和采樣合并起來，利用較少的信號投影測量數據量，根據相應的重構算法，最終重構出較為完整的信號[1-2]。

壓縮感知技術在穩定中發展，在不同的研究領域中都有體現，尤其是在信道估計領域中。傳統的信道估計方法如最小二乘(LS)法[3]和最小均方誤差(MMSE)法[4]都需要大量的導頻信號才能做出準確的

估計，并且這些方法主要針對的是密集型信道。由于近些年的研究我們可以知道，實際條件下的信號多數都是稀疏的，如果依舊不顧效率采用大量的導頻信號，會造成資源的嚴重浪費。貪婪算法[5]是壓縮感知重構算法中極為重要的一類算法，其中匹配追蹤MP(matching pursuit)、正交匹配追蹤算法OMP(orthogonal matching pursuit )[6]、廣義正交匹配追蹤(GOMP)算法[7]均已在稀疏信道估計中得以應用[8-10]。但是，MP與OMP算法在應用時所需要的迭代次數過多，所需時間較長，導致重構效率不高。GOMP算法雖然在重構時間上較OMP算法有所提高，但是由于選擇原子的方法不夠完備，再加上原子數目的增加，使其最小均方誤差(MSE)和誤碼率(BER)略差。而且OMP和GOMP算法的實現都需要稀疏度已知為前提才可實現，而實際環境這一前提無法滿足，導致了這幾種算法在信道估計中的局限性。本文提出改進的GOMP算法在不知曉稀疏度的情況下，通過變步長實現稀疏自適應匹配，并利用傅里葉變換的共軛對稱性在原子的選擇方面加以完善，提高了算法的應用價值。

1　壓縮感知技術

壓縮感知技術的本質，也就是把壓縮和采樣合二為一，即采樣的過程也就是完成壓縮的過程，經壓縮感知采樣后的數據本身也就是壓縮后呈現的數據。通過對原始信號的一種提取后的精煉表達，減少了原始數據在存儲空間或者傳輸帶寬方面的需求。

運用壓縮感知技術，需要關注的重點有兩個。第一個是怎樣設計出一個測量矩陣Φ，使得它可以在采樣的整個過程中包含著信號中較為有效的信息[11]；第二個是怎樣通過測量矩陣y重構原始信號x[12]。為此應該研究測量矩陣Φ應該具備的性質。首先應從確保重構的必要條件零空間特性開始。但是論證零空間特性是確保重構的必要條件這一過程中，并沒有考慮到噪聲的影響，所以在面向實際條件時，有必要在更為嚴格的情況下進行推導。這一點上促使有限等距性質RIP(restricted isometry property)在整個壓縮感知理論中具有了重要地位[13]，即：

若存在δk∈(0,1)，使得：

(1)

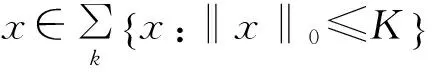
2　算　法

2.1　OMP算法

正交匹配追蹤(OMP)算法與之前的算法相比，保證了殘差和已選列正交的這一條件，從而使相同的列并不會再一次被選中，減少了迭代的次數，優化了整個迭代的過程[15]。

OMP算法的本質是通過貪婪策略在Φ中來挑選一列原子。OMP算法首先選擇原子φi∈Φ，然后將觀測信號投影到原子上，以獲得殘差[16]。這些可以描述為:

y=ri+<φi,y>φi

(2)

它的目的是選擇出使殘差的二范數最小的原子。其中r1和<φi,y>φi明顯是正交的，因此：

(3)

(4)

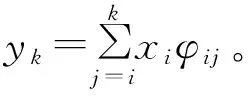
在每次迭代中，新的原子總是和殘差保持正交關系。當迭代停止時，獲得重建信號。這也就是OMP算法的基本原理。雖然OMP算法對于滿足RIP性質的信號都可以做到較高精度的重構[17]，但是當原始信號具有較大長度時，OMP算法仍然只在一次迭代中選擇一個原子，因此需要更多的迭代次數來進行原子的選擇，必然會導致重構時間的大幅度增長，使得重構的效率低下。而在實際的信道估計領域中，其他算法整體重構精度的提高，無疑使算法的復雜度成為其走向實際應用的最大障礙。再加上OMP算法需要信號的稀疏度作為先驗信息，也極大程度地限制了它的發展。

2.2　GOMP算法

GOMP算法在選擇原子這一方面較OMP算法進行了改進[18]。GOMP算法首先計算內積。

C={ci|ci=yTφii=1,2,…,N}

(5)

OMP算法選擇最相關的原子，其對應于C中的最大系數。但GOMP算法在每個迭代步驟中選擇n個頂部原子(ci1,ci2,…,cin)。然后使用式(4)獲得y的近似值，并使用以下公式更新殘差：

(6)

式中：ΦΛ是由選自于Φ的原子所組成的子矩陣。

GOMP算法的具體步驟如下：

已知觀測向量y，傳感矩陣Φ，原子選擇數S(S≤K)，迭代次數t。

(1) 進行初始化：r0=0,H=φ,t=0,J=φ。

(2) 令迭代次數增加：t=t+1。

(3) 計算相關系數：Ct=ΦTrt-1。

(4) 從計算出的Ct中挑選出最大的S個原子，然后將這些原子添加到集合J中。

(5) 更新索引集：H=H∪J。

由以上可知，選擇原子數目的增加使得GOMP算法在收斂速度上比OMP算法要快得多，重建效率也有了提升，但需要提前了解稀疏度K這一不足仍沒有得到較好的改進。對于原子選擇方面，有研究結果表明，當時域信號將傅里葉基作為稀疏基時，重構過程中出現的少量的對頻譜的估計錯誤，也將會很大程度上影響重構的精度[19]。如果僅是利用相關性來進行原子的選擇，會使選擇具有盲目性。并且在觀測過程中出現大量噪聲的情況下，容易出現更多的估計錯誤，從而導致原子匹配程度和支撐集選擇的準確性降低，進而影響信號重構的成功率。因此，應該從如何適應在稀疏度K未知情況下重建信號，以及如何更準確更穩定地選擇原子這兩方面同時對GOMP算法加以改進。

2.3　改進的GOMP算法

原始信號x與各個原子之間的相關性在持續迭代的過程中有所下降[20]。先前幾次迭代中所選擇的原子體現的作用更大，選擇的不確定性導致的原子錯誤將會對整個結果產生更大的影響。因此，在早期的迭代過程中，我們將選擇原子的個數設置為一個較小的數值，以免選擇出大量的錯誤原子。而后，當殘余量減少緩慢的時候，逐漸增大S的取值。

其次，通過把傅里葉變換的共軛對稱性與之前利用相關系數這一選擇原子的唯一依據相結合，增強原子選擇的準確性，以增強整個算法的成功率。下面對傅里葉變換的共軛對稱性進行分析。

若f(t)為實信號，則它的傅里葉變換為F(jω)[21]，可以如下表示：

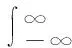
(7)

考慮到r-jωt=cosωt-jsinωt，則式(7)可寫為：

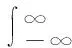
R(ω)-jX(ω)=|F(jω)|ejφ(ω)

(8)

式中：頻譜函數的實部與虛部以及模量與相角均為ω的實函數，并分別為：

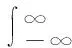
(9)

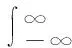
(10)

(11)

(12)

由式(9)-式(12)可知，頻譜函數的實部與模量是頻率ω的偶函數，虛部與相位是頻率ω的奇函數。

如果f(t)是t的偶函數，則式(10)的積分為零，其頻譜函數僅有實部，是ω的實偶函數。即:

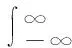
(13)

由此可以得到:F(jω)=F*(-jω)。

如果f(t)是t的奇函數，則式(9)的積分為零，其頻譜函數僅有虛部，是ω的虛奇函數。即:

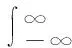
(14)

由此可以得到:F(jω)=-F*(-jω)。

研究可知，大多數的時域信號在傅里葉基中都能保持有良好的稀疏性。當把傅里葉基作為稀疏基時，信號的各個采樣點都能找到以信號的采樣頻率的一半為中心與自身對稱的點，也就是傅里葉變換的共軛對稱性[22-23]。

改進的算法將傅里葉基作為稀疏基，以使信號具有傅里葉共軛對稱的性質。在選擇原子的時候，只是對相關系數的前一半進行篩選，選擇出相關性最高的S個原子，將它們的下標添加進入集合J中。之后利用傅里葉變換的共軛對稱性對剩余的原子進行選擇，也就是在剩余的相關系數中找出與添加進入集合J的原子的對稱點即可，然后一并加入到集合J中。此時，集合J中有2S個原子，只需要在這里挑選出最匹配的S原子再加入新的集合中即可。

雖然OMP與GOMP算法選擇原子的數目不相同，但都是以相關性作為選擇原子的唯一標準。兩者需要將全部相關系數進行比較，從中篩選出相關性最高的一個或幾個原子。相比較來說，改進后的算法只需要對前一半相關系數進行處理，另一半可以在前一半的基礎上得出，從而提高了原子選擇的效率。并且在利用了傅里葉變換的共軛對稱性的情況下，兩種標準相互輔助，使原子的選擇更加針對和可靠，當觀測過程出現大量噪聲時候仍能有效控制原子選擇這一過程，進而提高了原子選擇的精度。

改進的GOMP算法的具體步驟如下：

已知觀測向量y，傳感矩陣Φ，原子選擇數S(數值較小)，迭代次數t。

(1) 進行初始化：r0=0,H=φ,t=0,J=φ,Q=φ。

(2) 令迭代次數增加：t=t+1。

(3) 計算相關系數：Ct=ΦTrt-1。

(4) 在步驟(3)計算出的相關系數Ct的前半部分中選出最大的S個原子，然后將這些原子的下標添加到集合J中。

(5) 對于剩余部分，利用傅里葉變換的共軛對稱性，將與添加到集合J中的原子下標所對稱的點找出來，同樣加入到集合J中。最終，在集合J中選出最大的S個原子組成新的集合Q。

(6) 更新索引集：H=H∪Q。

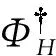
其中,ε1就是GOMP算法中的閾值，它的取值受原始信號中噪聲的影響；而ε2是為了判斷殘差減少的程度，低于這個取值的時候，選擇原子的個數將不會再增加。在大量實驗的驗證下，本文將ε2的取值設置為0.7，并應用于接下來的仿真實驗中。

以上就是改進的GOMP算法的具體步驟。針對上文提到的先前算法的不足之處，通過可變步長來實現稀疏自適應匹配，并利用傅里葉變換的共軛對稱性增強選擇原子的效率和準確性。

3　實驗仿真與驗證

在理論的基礎上，本文通過如下的仿真實驗，從不同的參考角度與之前的兩種算法進行對比，證明改進后的GOMP算法在信道估計性能方面的優越性。仿真硬件為Intel(R) Core(TM) i5-3230M CPU，主頻為2.6 GHz，內存為8 GB，Microsoft Windows 7操作系統，仿真軟件為MATLAB。

仿真如下，假設天線方案為2根發射天線和2根接收天線，系統子載波個數為1 024，導頻數為25，信道長度為30，并且信道參數在一個OFDM符號內保持不變。利用算法的歸一化均方誤差(MSE)和誤比特(BER)來反映幾種算法的估計性能[18]，MSE的定義為：

(10)

二者數值越小，代表估計的性能越好，反之亦然。

圖1 是不同信噪比情況下，三種算法的MSE數值大小比較。不難看出，信噪比的不斷增大，使得三種算法的MSE數值均呈現一種下降的趨勢。但從整體來說，改進后的GOMP算法與另外兩種相比數值更小。而在任意相同的條件下，改進后的GOMP算法都比另外兩種的MSE數值要低，凸顯了性能的優越性。

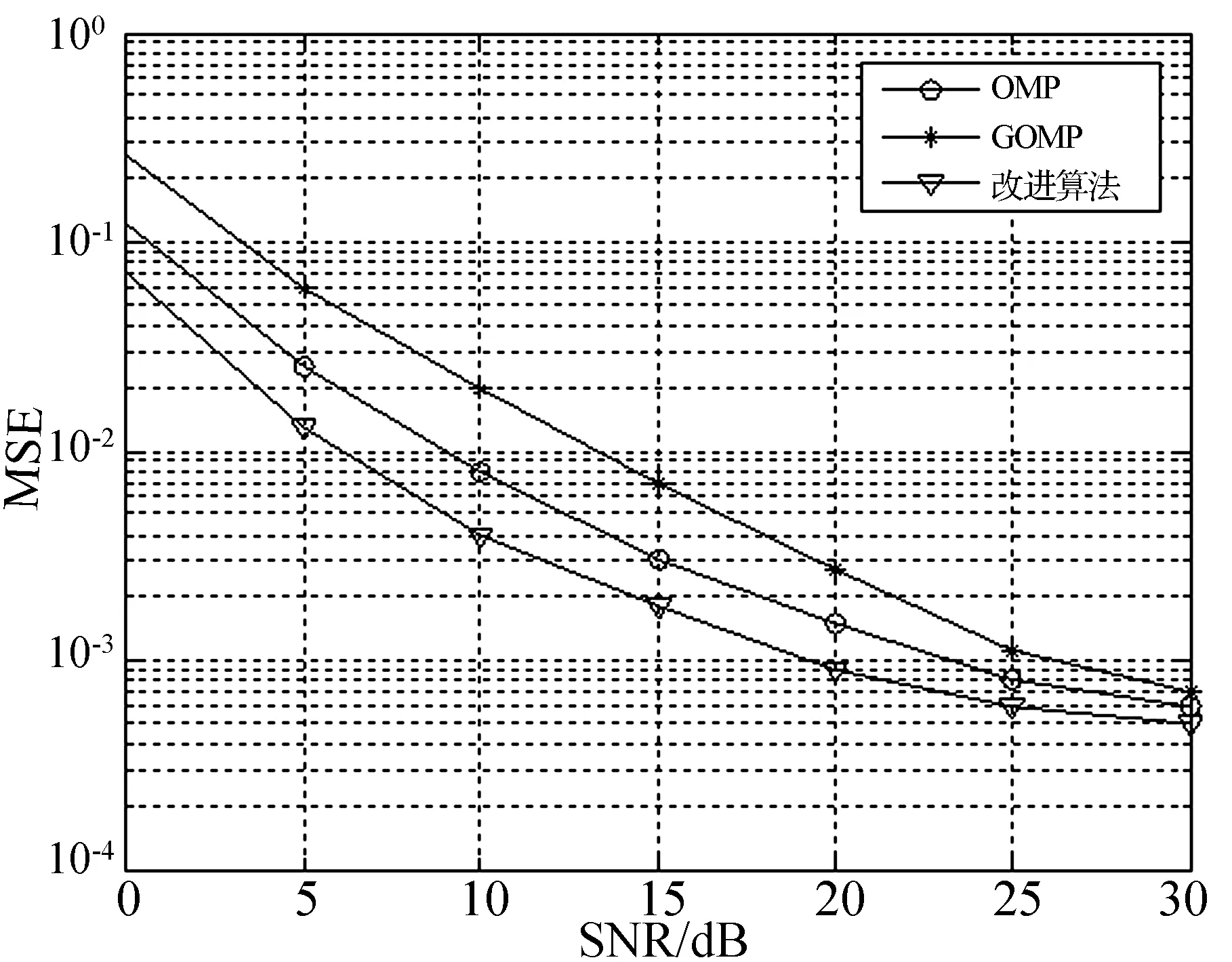
圖1　不同信噪比條件下三種算法的MSE性能比較

圖2展示了三種算法在不同信噪比情況下的BER性能比較。可以看出，信噪比的不斷增大，說明了信號干擾逐漸減小。因此三種算法的BER數值都會降低。改進的GOMP算法與另外兩種對比來說，幅度更大，趨勢更強，BER數值更小。由此說明，改進的GOMP算法具有更好的性能。

圖2　不同信噪比條件下三種算法的BER性能比較

由于選擇原子數量S的不斷增大，每一次增大程度n的取值不同也對算法的性能產生影響。圖3是改進的GOMP算法在S的數值大小相同而n的不同取值情況下，與OMP算法和GOMP算法在迭代次數方面的比較。從理論上來說，GOMP算法及其改進算法在選擇原子的數目上面要多于OMP算法，所以說在這一方面上必然比OMP算法更有效率。由圖中還可以看出，改進的GOMP算法對稀疏性具有良好的適應性，無論K值如何，算法都能很好地進行，而OMP算法在這一方面顯示出了不足。對于n的取值來說，迭代的次數會隨著n取值的增大而減小，但精確度并不會因此而降低。

圖3　OMP算法和GOMP算法的比較

峰值信噪比(PSNR)是一種評價圖像的客觀標準，PSNR公式如下：

(11)

式中:X和X1分別代表原始信號和重構信號。

表1中顯示了三種算法的PSNR值和運行時間。由表可以看出，三者的PSNR值相差不多，改進的算法可以很好地適應稀疏性，保證了重構的效果。在運行時間方面，GOMP算法及其改進算法較OMP算法都有大幅度的提高。驗證了改進的算法在保證了重構效果的同時提高了效率。

表1　各算法PSNR值和運行時間

4　結　語

本文根據壓縮感知理論知識以及信道的特性，提出了一種基于壓縮感知改進的廣義正交匹配追蹤算法。此算法與先前的GOMP算法相比，可以實現自適應匹配，無需預先知道稀疏度，并且在原子選擇方面進行了優化。由仿真實驗的結果可以看出，提出的算法可以有效地提高重構信號的精度和效率，并在此基礎上降低了傳統算法的復雜度，使該算法可以更好地應用在信道估計領域中。

[1] 焦李成，楊淑媛，劉芳,等.壓縮感知回顧與展望[J].電子學報，2011,39(7)：1651-1662.

[2] Donoho D L, Tsaig Y. Extensions of compressed sensing [J]. Signal Processing, 2006,86(3):533-548.

[3] Tropp J A, Gilbert A C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit [J]. IEEE Transactions on Information on Information Theory, 2007,53(12):4655-4666.

[4] 李然,干宗良,崔子冠,等.壓縮感知圖像重建算法的研究現狀及其展望[J].電視技術,2013,37(19):192-196.

[5] Kim Seung-Jean, Koh K, Lustig M, et al. An Interior-Point Method for Large-Scale l1-Regularized Least Squares[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 606-617.

[6] 何雪云，宋榮方，周克琴. 基于壓縮感知的OFDM系統系數信道估計新方法研究[J].南京郵電大學學報，2010,30(2)：60-65.

[7] Wang J, Kwon S, Shim B. Generalized orthogonal matching pursuit[J]. IEEE transactions on signal processing, 2012(60):6202-6216.

[8] Cotter S F, Rao B D. Sparse channel estimation via matching pursuit algorithm [J]. IEEE transactions on Communications, 2002,50(3):374-377.

[9] Karabulut G Z, Yongacoglu A. Sparse channel estimation using orthogonal matching pursuit algorithm[J]. IEEE 60th Vehicular Technology Conference, 2004. VTC2004-Fall. 2004.

[10] 甘偉，許錄平，羅楠, 等.一種自適應壓縮感知重構算法[J].系統工程及電子設計，2011,33(9)：1948-1953.

[11] 呂偉杰，陳霞，劉紅珍.基于壓縮感知的自適應匹配追蹤優化[J].系統工程與電子技術，2015,37(5)：1201-1205.

[12] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4):1289-1306.

[13] Fiqueiredo M A T, Nowak R D, Wright S J. Gradient projection for sqarse reconstruction: application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007,1(4):586-597.

[14] 甘偉，許錄平，蘇哲.一種壓縮感知重構算法[J].電子與信息學報，2010,32(9)：2151-2155.

[15] 趙龍慧，潘樂炳，李寶清.OFDM稀疏信道估計中改進的OMP算法[J].計算機工程與設計，2015,36(7)：1701-1705.

[16] Davenport M A, Boufounos P T, Wakin M B, et al. Signal Processing With Compressive Measurements[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2):445-460.

[17] 石光明，劉丹華，高大化.壓縮感知理論及其研究進展[J].電子學報，2009,37(5)：1070-1081.

[18] 呂方旭, 張金成, 王泉,等. 基于傅里葉基的自適應壓縮感知重構算法[J]. 北京航空航天大學學報, 2014, 40(4)：544-550.

[19] 朱延萬，趙擁軍，孫兵.一種改進的稀疏度自適應匹配追蹤算法[J].信號處理，2012,28(1)：80-86.

[20] 王妮娜，桂冠，蘇冰濤，等.基于壓縮感知的MIMO-OFDM系統稀疏信道估計方法[J].電子科技大學學報，2013,42(1)：59-62.

[21] 趙龍慧，潘樂炳，李寶清.OFDM稀疏信道估計中改進的OMP算法[J].計算機工程與設計，2015,36(7)：1701-1705.

[22] 高西全，丁玉美.數字信號處理[M].西安：西安電子科技大學出版社，2008：84-87.

[23] 楊盼.壓縮感知中改進的匹配追蹤類算法研究[D].安徽：安徽大學，2015.