局部一致性的信息熵Relief特征加權算法

張　敏　徐　棟

1(山東管理學院機電學院　山東 濟南 250357) 2(北京理工大學信息與電子學院　北京 100081)

0　引　言

特征選擇作為維度削減技術中的熱門研究課題，分為過濾法和封裝法。封裝法依賴分類器的選擇，分類效果因分類器選擇的不同而產生巨大差異。過濾法因不依賴分類器得到較廣泛的關注。Relief算法是一種過濾算法，用于二類數據的特征選擇。雖然Relief算法較早提出且得到廣泛應用，但該算法依然存在缺陷，如算法的數學定義形式較抽象，性質難以解釋，且對噪聲和野點魯棒性較差。ReliefF和Multi-Relief算法[1]作為Relief的推廣是處理多類數據的算法，通過將多類問題轉化為多個一對多的兩類問題。文獻[2]提出迭代Relief (I-Relief)算法，I-Relief算法的目標函數的構造是在間隔最大化基礎上，并借助類EM的學習策略來更新權重向量的規則，有效彌補了Relief算法對目標函數定義不明確的缺點。

基于上述進展，本文在優化目標函數中引入正則項因子，使分類正確樣本周圍樣本的分類結果保持較高的分類一致性，減小分類錯誤率。用模糊隸屬度構造新的模糊差異度量，并且基于信息熵原理，重新構造了新的間隔最大化目標函數。探討了具有更好適應性二類數據的魯棒Relief特征加權算法，并進一步將算法擴展到多類數據的算法。

1　局部一致性的信息熵Relief算法

1.1　Relief和間距最大化

Relief算法的每個特征向量對不同樣本有不同的區分能力，其算法是借助這種區分能力來估計特征權值及其重要性。具體算法如下：

(2) 任選樣本xn,計算其同類最近鄰樣本NH(xn)和異類最近鄰樣本NM(xn)。

(3) 根據式(1)、式(2)更新權值wj:

(1)

(2)

(4) 當t=T時，算法結束，否則返回步驟(2)。

(5) 輸出迭代后的權值向量w。

文獻[4]初次提出Relief算法和間距最大化的關系，并將其應用于特征選擇。文獻[2]基于間距最大化對Relief算法進行了具體的數學推理證明，公式如下所示：

s.t.|w|22= 1,w≥0

(3)

式中：ρn(w)表示第n個樣本對應的間距大小。

該目標函數存在如下缺陷:1) 特征權值較易集中于某一個值，忽略其他權值，自適應性較差。2) 不能有效地去除冗余特征，對噪聲和野點有較差的魯棒性，分類錯誤率高。

針對Relief算法以上缺陷，本文引入如下技術：1) 信息熵控制；2) 模糊差異性度量；3) 分類局部一致性。

1.2　信息熵Relief算法

傳統的Relief特征加權算法在構造目標函數時特征權值分布不均勻，易集中于某一個特征。實際上目標函數的構造應根據樣本的重要性賦予不同的權值。信息熵[3]表明每個消息所提供的平均信息量。熵和樣本在屬性域上的分布成正比，熵越大，樣本分布越均勻。引入信息熵理論公式如下所示：

(4)

目標函數的間距最大化使特征權值容易趨向于某一分量，引入最大信息熵，使各權值的概率分布盡可能均等，改善了Relief算法自適應差的缺陷。

1.3　模糊差異性度量

Relief算法中，差異性度量受噪聲和野點的影響較大。本研究采取樣本與近鄰的p個樣本的差異的均值取代。

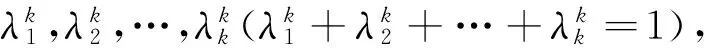
(5)

模糊隸屬度公式如下所示：

(6)

新的差異性度量公式如下所示：

(7)

xn到最近異類樣本和最近同類樣本的第j維特征的模糊差異度量表示公式如下所示：

(8)

式中：NM(xn)代表除xn以外的所有和xn異類的樣本集合；NH(xn)代表除xn以外的所有和xn同類的樣本集合。

1.4　局部一致性Relief算法

為提高分類準確率，對目標訓練數據施加約束條件，即在Relief算法基于分類邊界的全局優化框架中引入額外的局部一致正則項，公式如下所示：

(9)

(10)

(11)

Yij=|yi-yj|

(12)

算法加入正則項因子， 以相鄰樣本間的相似性為度量，使分類正確樣本周圍樣本的分類結果保持較高的分類一致性，提高了分類準確率。

2　局部一致性的信息熵Relief特征加權算法

2.1　新的優化目標函數

結合信息熵Relief算法、模糊差異性度量、局部一致性Relief，得出新的優化目標函數公式如下所示：

(13)

s.t.|w|22= 1,w≥0

對式(13)做如下說明：目標函數由3項組成。其中第1項對應于間距最大化，第2項對應于特征加權的信息熵，第3項對應于局部分類一致性。參數λ、η是常量，用于平衡各項的貢獻。

2.2　理論推導

對于式(13)的優化目標函數，運用拉格朗日定理，可得以下定理。

定理：目標函數J(w)滿足式(14)時，取得最大值。

(14)

證明：對式(13)構造拉格朗日函數得：

式中：β>0為拉格朗日因子。

置L(wj,β)對變量wj、β的偏導數為0,可得式(15)-式(17)：

(15)

(16)

由式(15)得:

(17)

聯合式(16)、式(17)得：

算法1基于二類數據的局部一致性信息熵Relief特征加權算法LIE-Relief-T。

(3) 根據式(14)更新權值wj(t)。

(4) 若t=T或|w(t)-w(t-1)|<θ，算法結束，否則返回(2),且使t=t+1。

(5) 輸出更新后的w。

2.3　基于多類數據的局部一致性信息熵Relief特征加權算法

本節將LIE-Relief-T算法擴展到多類版本LIE-Relief-M算法，采用的策略是不論異類樣本被劃分為多少類，將所有異類樣本作為同一類數據處理[5]。則xn對應的樣本間距公式如下所示：

(18)

(19)

(20)

根據2.2節的推導方法，可得多類數據輸出權值：

3　實現驗證

3.1　實驗數據

為了驗證LIE-Relief-T算法和LIE-Relief-M算法的性能，本實驗采取的數據集為UCI基準數據集和基因表達數據集[6]，如表1-表2所示。

表1　UCI數據集

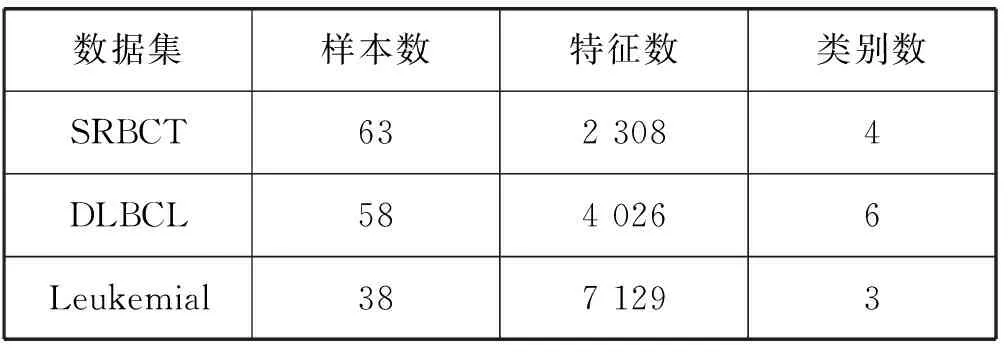
表2　基因表達數據集

為了測試LIE-Relief-T算法和LIE-Relief-M算法確定有效特征的能力，在UCI數據集每個樣本中加入干擾特征(二類數據90個，多類數據45個)，并將UCI數據集按照5∶1的比例隨機分為訓練集和測試集，將訓練集比例10%的樣本錯貼類標簽作為野點。對基因表達數據集采用leave-one-out策略進行分類測試。

3.2　實驗設置

本文提出的LIE-Relief-T二類數據集算法，使之與經典的Relief算法、Simba算法[7]、I-Relief算法[2]、f-MMD算法[8]的性能進行對比；LIE-Relief-M多類數據集算法與ReliefF算法[9]、I-Relief-2算法[10]的性能進行對比。

實驗所用計算機為Intel(R) Core(TM) i5-4210M, 2.60 GHz的CPU,4.0 GB的內存，Win7操作系統，Matlab2009版本。

實驗選用K-NN分類器[11],K值由交叉驗證策略確定。

3.3　實驗結果

以ROC(Receiver operating characteristic)曲線和分類錯誤率為評價標準評估實驗結果。圖1-圖2為各種算法在UCI數據集上運行10次取平均值后得到的ROC和分類錯誤率曲線。

圖1　不同算法在UCI數據集上的ROC曲線圖

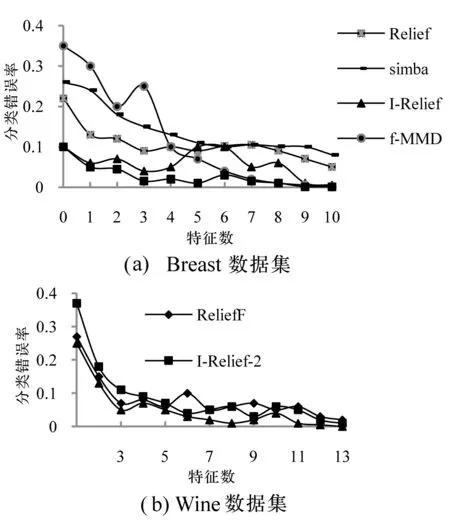
圖2　不同算法在Breast/Wine數據集上的分類錯誤率比較

其中，圖1為算法的ROC曲線圖，圖2分別抽取了UCI數據庫的Breast和Wine數據集。從圖1、圖2能直觀得出，本文算法因增加信息熵和局部分類一致參數模型，較傳統的算法分類錯誤率更小，具有更明顯的優越性或競爭。

圖3中，dw=‖w(t)-w(t-1)‖，LIE-Relief-M算法的誤差較小，經過較少的迭代次數收斂性曲線即達到穩定狀態。

圖3　LIE-Relief-M算法在Wine數據集上的收斂曲線

圖4為多類算法在Wine數據集上的特征權值變化曲線。其中前13維特征來自Wine數據集，后45維特征是手動添加的干擾特征，理想情況下后45維特征的權值越小越好。由曲線可得：ReliefF算法的干擾特征權值最大且穩定性最差，LIE-Relief-M算法加入信息熵控制，使算法對例外點和野點的魯棒性增強，干擾特征權值最小且接近于0，且干擾特征權值變化曲線收斂性較好。同樣，在其他UCI數據集上得到了類似的實驗結果。

圖4　不同算法在Wine數據集上的權值向量對比

基因表達數據集均為高維數據，沒有添加干擾因素，采用分類錯誤率為實驗評估標準。如圖5所示。

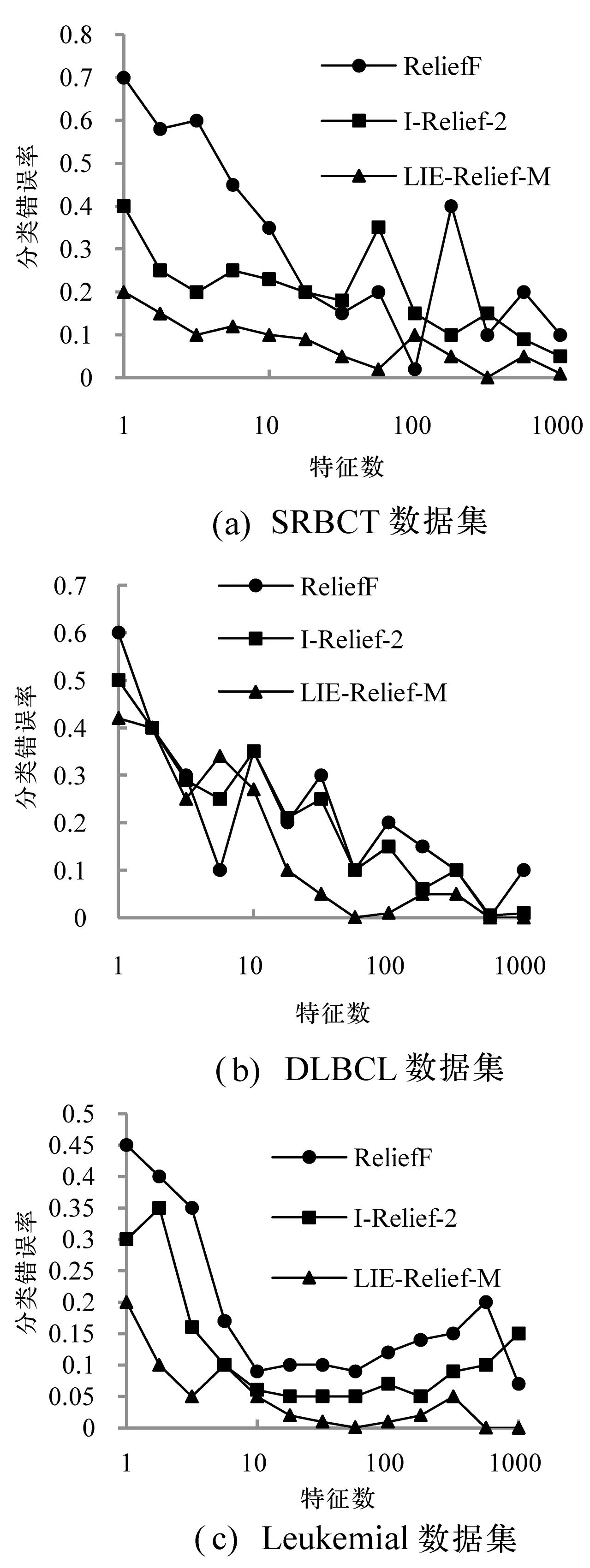
圖5　不同算法在基因表達數據集上的分類錯誤率比較

由圖5可得，LIE-Relief-M算法因加入分類局部一致性參數因子，在基因表達數據集上的分類錯誤率最小，較其他兩種算法具有更好的分類性能。

4　結　語

本文在Relief算法的基礎上，基于信息熵、模糊差異性度量、分類局部一致性提出LIE-Relief-T二類數據算法，并將其擴展到多類LIE-Relief-M算法。在UCI和基因表達數據集上分別驗證了LIE-Relief-T算法和LIE-Relief-M算法。實驗結果表明新算法不但分類錯誤率低，對野點和噪聲也具有更好的適應性和魯棒性。未來的工作中，對算法參數選擇的理論依據、開發適合大規模數據集的快速Relief特征加權算法將是研究的方向。

[1] Ye K,Feenstra K A,Heringa J,et al.Muiti-RELIEF:a method to recognize specificity determining residues from multiple sequence alignments using a Machine-Learning approach for feature weighting[J].Bioinformatics,2014,24(1):18-25.

[2] Sun Y.Iterative RELIEF for feature weighting:Algorithms,theories,and applications[J].IEEE Trans on Pattern Analysis and Machone Intelligence,2013,29(6):1035-1051.

[3] Shannon C E.A mathematical theory of communication[J].Bell System Technical Journal,1948,27(3):379-423.

[4] Gilad B R,Navot A,Tishby N.Margin based feature selection-Theory and algorithms[C]//ICML’04 Proceedings of the twenty-first international conference on Machine learning.ACM,2004:43.

[5] 陳俊穎,陸慧娟,嚴珂,等.Relief和APSO混合降維算法研究[J].中國計量大學學報,2017,28(2):214-218.

[6] Sun S L,Xu Z J,Yang M.Transfer learning with part-based ensembles[J].Lecture Notes in Copmuter Science,2013,7872:271-282.

[7] Sun Y,Wu D.A RELIEF Based Feature Extraction Algorithm[C]//Siam International Conference on Data Mining,SDM 2008,April 24-26,2008,Atlanta,Georgia,Usa.DBLP,2008:188-195.

[8] Selen U,Jaime C.Feature Selection for Transfer Learning[C]//European Conference,ECML PKDD 2011,Greece,2011:430-442.

[9] Robnik M,Kononenko I.Theoretical and empirical analysis of Relief and RRelief[J].Machine Learning,2014,53(102):23-69.

[10] Theodoridis S,Koutroumbas K.Pattern Recognition[M].3rd ed.New York:Academic Press,2013:44-60.

[11] Jing L P,Ng M K,Huang J Z.An Entropy Weighting k-Means Algorithm for Subspace Clustering of High-Dimensional Sparse Data[J].IEEE Transactions on Knowledge & Data Engineering,2007,19(8):1026-1041.