基于煙花算法的非合作博弈Nash均衡問題求解

楊彥龍　向淑文，　夏順友　賈文生

1(貴州大學計算機科學與技術學院　貴州 貴陽 550025) 2(貴州大學數學與統計學院　貴州 貴陽 550025)

0　引　言

隨著經濟全球化深入發展，博弈論研究持續活躍，特別是諾貝爾經濟學獎多次授予從事博弈論研究與應用的學者，博弈論被廣泛地應用到經濟學、社會學、計算機科學等許多領域。Nash均衡是非合作博弈最核心的概念，關于Nash均衡的研究主要涉及存在性、穩定性及機制設計等。由于Nash均衡問題的算法是PPAD-Complete，因此關于Nash均衡問題的算法研究相對較為棘手。Lemke和Howson提出了二人有限非合作博弈模型的互補轉軸算法，即Lemke-Howson算法[1]；Govindan等[2]利用結構定理及同論方法提出了一種全局Newton算法；Zhang等[3]利用擬變分不等式提出了廣義博弈模型的投影算法；Herings等[4]提出了的同倫算法；Yuan[5]利用信賴域算法計算Nash均衡，并證明了在一定條件下該算法是全局收斂且局部超線性逼近。以上算法為數值算法，該類算法保證了算法的收斂性，意義在于證明了博弈問題的可計算性，但計算方法較為復雜且運行時間較長。近年來，學者受某些自然界生物進化的啟發，利用一些智能算法計算Nash均衡，比如：蟻群算法、遺傳算法、粒子群算法等智能算法[6-9]。智能算法為Nash均衡計算提供了新的研究方法和途徑。受煙花在夜空中爆炸產生火花照亮周圍區域這一現象的啟發，Tan等[10]提出了煙花算法(FWA)。煙花算法屬于啟發式算法，利用爆炸算子、高斯變異和選擇策略較快地尋找到全局最優解，隨后許多學者對煙花算法進行了研究及應用，關于煙花算法的最新研究進展參考文獻[11-12]。文獻[13]提出了融合佳點集變異機制的動態搜索煙花爆炸算法。文獻[14]引入淘汰機制，提出了一種混沌煙花搜索算法。文獻[15]將煙花算法應用于云計算多目標任務調度。文獻[16]應用煙花算法求解JSP問題。文獻[17]提出了多目標煙花算法并應用于施肥問題。本文基于煙花算法求解N人有限非合作博弈的Nash均衡，并通過與文獻[8-9]中免疫粒子群算法的比較，實驗結果驗證了該算法的有效性。

1　問題描述

設N人有限非合作博弈模型用三元組Γ(N,{Si}i∈N,{ui}i∈N)表示，其中N表示局中人的個數，Si={si1,si2,…,sim}表示局中人i的有限個策略的策略集，S=S1×S2×…×SN表示N個局中人的策略乘積空間，ui:S→表示局中人i的收益函數。對于任意策略組合s=(s1,s2,…,sN)∈S，為了表述方便，用表示在策略組合s中局中人i的策略替換為其他局中人的策略不變；以下公式中出現類似的表示，意義與此相同。

稱Si={si1,si2,…,sim}的凸組合集Xi={(xi1,xi2,…,xim)|xi1+xi2+…+xim=1,xij≥0}為局中人i的混合策略空間，xi∈Xi表示局中人i選取純策略的概率分布，X=X1×X2×…×XN表示N個局中人的策略乘積空間，局中人i的收益函數仍用ui:X→表示。

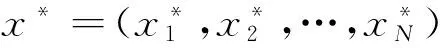
顯然，純策略Nash均衡是混合策略Nash均衡的特殊情況。

性質1混合策略均衡x*是Γ的Nash均衡解的充分必要條件是：對于任意的局中人i的每一個純策略sij(1≤j≤im)，有ui(x*)≥ui(x*;sij)成立。

若N=2，則Γ是雙矩陣博弈，局中人的收益分別用矩陣A、B表示，則是雙矩陣博弈一個Nash均衡解的充分必要條件是：

2　煙花算法的設計

2.1　煙花算法的基本思想

煙花算法是受煙花在夜空中爆炸產生火花這一現象的啟發演變而來的群體智能算法。在煙花算法中，每一個火花被看作問題解空間的一個可行解，根據火花爆炸的范圍和強度，設定的爆炸搜索機制產生下一代火花群體，對于適應度值較好的火花，在下一代中在較小范圍內產生較多的火花；對于適應度較差的火花，在下一代中消失或者發生變異。允許一定數量的火花發生變異，增加火花種群的多樣性，避免算法過早陷入局部收斂。如此循環下去直到產生滿意的火花為止。在煙花算法中，有三個重要組成部分：爆炸算子、變異算子和選擇策略。各類算子的設計決定了煙花算法的優劣。

煙花算法具體步驟如下：

Step1在可行域內隨機產生一定數量的煙花。

Step2根據爆炸算子，計算每個煙花的爆炸半徑和火花數量，生成每個煙花的火花，根據變異算子產生變異火花。

Step3判斷是否滿足停止條件，否則進入Step4。

Step4根據選擇策略，選出下一代煙花，返回Step2。

2.2　Nash均衡求解的煙花算法設計

算法中每一個煙花表示所有局中人的混合策略x=(x1,x2，…,xm)，定義N人有限非合作博弈Nash均衡求解的適應度值函數為：

根據性質1可知，若x*為N人有限非合作博弈的Nash均衡解的等價條件為：f(x*)=0。

特別地，對于2人有限非合作博弈Nash均衡求解的適應度值函數為：

式中:Ai.表示矩陣A的第i行向量，B.j表示矩陣B的第j列向量。同理可知，若x*為2人有限非合作博弈的Nash均衡解的等價條件為：f(x*)=0。

2.2.1爆炸算子

根據爆炸算子計算出煙花爆炸的半徑ri及產生的火花數量ki，其中:

2.2.2變異算子

為了避免算法過早陷入局部收斂，增加下一代火花種群的多樣性，引入高斯變異火花，即在煙花種群產生的火花中隨機選取1個(或幾個)火花xi，然后對選中的火花的1個(或幾個)維度xik執行如下操作：

式中：e～N(1,1)，即e服從均值為1，方差為1的高斯分布。

2.2.3選擇策略

在由煙花、火花、變異火花組成的候選集中，選出適應度值最小的n個個體作為下一代煙花。

本文算法的實現步驟如下：

Step1確定煙花的數目n，煙花爆炸最大半徑R，煙花群生成火花總數目K，最大迭代次數N，精度ε0。

Step2隨機產生n個煙花，計算每個煙花的適應度值，若適應度值滿足ε0，則進入Step7。

Step3根據爆炸算子計算煙花xi的爆炸半徑ri，及產生火花的數目ki，生成煙花xi的ki個火花，對火花進行越界檢測。

Step5計算火花、變異火花的適應度值，若滿足精度要求且未達到最大迭代次數則進入Step6，否則進入Step7。

Step6根據選擇策略選，在所有煙花、火花、高斯變異火花中選擇n個個體作為下一代煙花，進入Step2。

Step7運算停止。

3　數值實例

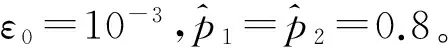
例1囚徒困境博弈Γ(X1,Y1,A1,B1)。

例2監察博弈Γ(X2,Y2,A2,B2)。

例3博弈Γ(X3,Y3,A3,B3)。

例4博弈Γ(X4,Y4,A4,B4)。

利用煙花算法求解例1，經過5次實驗，平均迭代9次給出了精確解，雖然文獻[8]用免疫粒子群算法平均迭代7次，但其適應度值的精度低于10-3。

利用本文的煙花算法求解例2，經過5次實驗，平均迭代12.8次，適應度值的精度達到10-3，文獻[8]用免疫粒子群算法平均迭代14次，但其適應度值的精度低于10-3。

在例4中，針對博弈策略矩陣為10階的高維方陣，引入離線性能函數比較煙花算法與粒子群算法搜索Nash均衡的能力，從圖形可以看出，在初始階段煙花算法較慢，但在后階段，煙花算法搜索效果明顯較好。

例1-例3的運算結果見表1-表3；例4的運算結果見圖1。

表1　例1的運算結果

表2　例2的運算結果

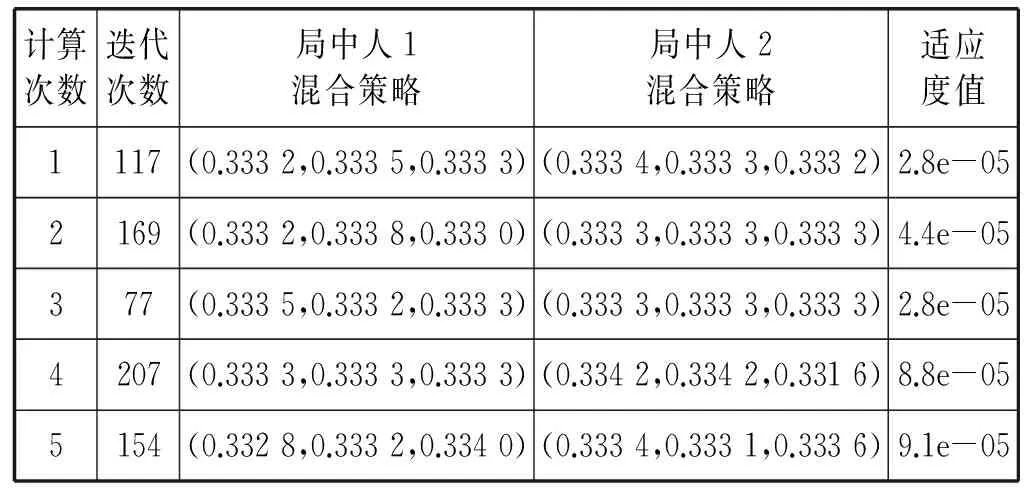
表3　例3的運算結果

圖1　fwa算法與pso算法的離線性能比較

4　結　語

通過以上的實例結果可知，煙花算法是求解N人有限非合作博弈Nash均衡問題的一種有效算法。煙花算法是一種群體智能算法，算法中參數設置較少，對目標函數要求較低，由于Nash均衡求解問題的計算是PPAD-Complete，其構造的適應度值函數又非一般意義下的函數甚至非光滑，這些問題本身的限制，使得煙花算法在求解Nash均衡時具有一定的優勢。今后將考慮分析不同的爆炸算子、變異算子和選擇策略對Nash均衡求解的影響，并考慮更復雜的Nash均衡求解問題。

[1] Lemke C, Howson J. Equilibrium points of bimatrix games[J].Journal of Society for Industrial and Applied Mathematics,1964,12(2):431-423.

[2] Govindan S, Wilson R. A global Newton method for computing Nash equilibria[J].Journal of Economic Theory,2003,110(1):65-86.

[3] Zhang Jian-zhong, Qu Biao, Xiu Nai-hua. Some projection-like methods for the generalized Nash equilibria[J].Computational Optimization and Applications, 2010, 45(1):89-109.

[4] Herings P J J,Peeters R. Homotopy methods to compute equilibria in game theory[J].Economic Theory, 2010,42(1):119-156.

[5] Yuan Ya-xiang. A trust region algorithm for Nash equilibria problems[J].Pacific Journal of Optimization, 2011,7(1):125-138.

[6] 邱中華,高潔,朱躍星. 應用免疫算法求解博弈問題[J].系統工程學報,2006,21(4):398-404.

[7] 王志勇,韓旭,許維勝,等.基于改進蟻群算法的納什均衡求解 [J].計算機工程,2010,36(14):166-171.

[8] 賈文生,向淑文,楊劍鋒,等.基于免疫粒子群算法的廣義Nash均衡問題求解[J].計算機應用研究,2013,30(9):2637-2640.

[9] 賈文生,向淑文,楊劍鋒,等.基于自適應小生境粒子群算法的多重Nash均衡求解[J].計算機應用與軟件,2015,32(1):247-250.

[10] Tan Y, Zhu Y. Fireworks algorithm for optimization[C]//International Conference on Advances in Swarm Intelligence. Springer-Verlag,2010:355-364.

[11] 譚營,鄭少秋.煙花算法研究進展[J].智能系統學報,2014,9(5):515-528.

[12] 譚營.煙花算法引論[M].北京：科學出版社,2015:23-28.

[13] 王培崇.融合佳點集機制的動態搜索煙花爆炸搜索算法[J].計算機應用與軟件,2015,32(8):248-251.

[14] 王培崇,李麗榮.改進的混合混沌煙花爆炸搜索算法[J].微電子學與計算機,2014,31(11):69-73.

[15] 黃偉建, 郭芳. 基于煙花算法的云計算多目標任務調度[J].計算機應用研究, 2017,34(6):1718-1720.

[16] 包曉曉, 葉春明, 黃霞. 煙花算法求解JSP問題的研究[J].計算機工程與應用, 2017,53(3):247-252.

[17] Zheng Y J,Song Q,Chen S Y.Multiobjective fire-works optimization for variable-rate fertilization in oil crop production[J].Applied Soft Computing,2013,13(11):4253-4263.