基于優選傅里葉描述子的粘連條銹病孢子圖像分割方法研究

邸馨瑤　焦　林　宋懷波

(西北農林科技大學機械與電子工程學院　陜西 楊凌 712100) (農業部農業物聯網重點實驗室　陜西 楊凌 712100)

0　引　言

小麥條銹病是小麥銹病的一種，是中國小麥生產中分布廣、傳播快、危害面積大的重要病害之一。小麥條銹病曾在全國范圍內大范圍流行，發生面積近670萬hm2，年損失約10億kg[1]。小麥條銹病一般流行年份可致減產10%～20%，特大流行年份減產可達60%以上，甚至絕產。如何實現條銹病的有效防控一直是我國農業研究領域的重點和難點。條銹病害病孢子呈鮮黃色，橢圓形，成株葉片初發病時夏孢子堆積為小長條狀，得到的孢子顯微圖像需要人工計數分析，誤差較大。如何實現粘連孢子的自動準確分割與計數對小麥條銹病孢子的在線檢測具有重要的研究意義。

目前，對于粘連目標的分割、計數已經取得了較大的進展。劉曉婉[2]采用基于邊界輪廓特征的算法，利用近似多邊形法和矢量點積與叉積的性質獲取分割點，實現了對粘連目標圖像的分割。葛亮等[3]針對光照不均勻的粘連細胞圖像，通過改進基于模板集精簡的算法，提高了顯微細胞圖像分割的效率。林小竹等[4]利用新型分水嶺分割算法，根據圖像中像素的4連通和集水盆地的邊緣情況實現了目標的準確計數。梁光明等[5]針對Canny算子在分割圖像過程中容易出現的粘連現象，結合目標圖像的基本形狀特征，實現了平滑目標輪廓，連接斷裂圖像邊緣的效果，提高了目標分割的準確性。Danielisa等[6]為實現了對人臉圖像的嘴唇分割，提出了超光譜圖像的嘴唇自動分割算法，基于傅里葉描述子對經過圖像增強及形態約束處理后的人臉圖像進行特征提取。繆慧司等[7]提出了一種結合距離變換與邊緣梯度分水嶺算法的顯微血細胞分割方法，實現了細胞的提取以及粘連細胞的自動分割。楊信廷等[8]為了檢測黃瓜葉片的濕潤情況，通過將原始圖像由RGB顏色空間轉換到L*a*b*顏色空間并利用歐式距離度量像素的相似度及K-means算法，實現了黃瓜葉片的水滴熒光圖像分割。Bao等[9]為了實現對腦磁共振圖像的分割，提出了基于特征敏感標簽融合的圖像分割方法。陳浩等[10]為實現對集捆后的棒材自動計數，提出了一種基于類圓形假設的圖像分割與識別方法。宋懷波等[11]在K-means聚類分割算法基礎上，提出了基于凸殼的重疊蘋果目標分割方法。

粘連孢子圖像存在圖像背景噪聲、孢子失活等問題，在已有的粘連目標分割、計數方法中，已較好地解決了粘連目標與背景分割的問題，但對多目標粘連的分割問題尚未很好解決。本文擬將K-means聚類算法與傅里葉描述子進行結合，在對目標準確分割的基礎上，基于傅里葉描述子方法，解決分割后目標輪廓不夠平滑的問題。然后，利用基于距離測度的角點檢測方法，實現粘連孢子角點的準確檢測，并進行粘連孢子的計數，以期為粘連孢子目標的準確識別提供新的借鑒。

1　實驗材料與方法

1.1　實驗材料

本文所用小麥條銹菌孢子是在西北農林科技大學植物保護學院實驗室培養條件下所得，將孢子與礦物油按體積1∶10相混合后滴加于載玻片上，用Olympus生物電子顯微鏡(型號：BX63，UCmos 14000KPA Pro系列真彩色高分辨率智能CCD顯微鏡數字攝像頭)采集圖像。圖像保存為4 096 Pixel×3 288 Pixel大小，JPEG格式。圖像采集裝置如圖1所示。實驗采用其中20幅圖像進行測試。

圖1　圖像采集裝置

所用圖像處理設備為臺式計算機，其配置為：CPU：Pentium(R)Dual-Core E5400 2.70 GHz；內存：3 GB。所有算法程序均在MATLAB 2009a上運行。

1.2　方　法

1.2.1孢子圖像分割

1) 孢子圖像預處理為了獲得更為一致的小麥條銹病孢子圖像，采用半徑為5的‘disk’形結構元素進行了閉運算處理[12]。預處理結果如圖2所示。

圖2　孢子圖像預處理

圖2(a)為在400倍放大下原始孢子的顯微圖像，圖2(b)為經過閉運算處理之后的孢子圖像。通過圖像對比可以看出，經過閉運算處理的圖像中原帶毛刺的粗糙邊緣變得平滑且原圖中影響計數的雜質點及孔洞得到填充，有利于圖像中目標孢子與背景雜質的分離，為孢子分割計數做準備。

2) K-means聚類算法介紹由圖2可以看出，受到雜質等干擾的影響，孢子的分割難度較大，為了實現孢子圖像的準確分割，本研究使用K-means聚類算法對孢子進行聚類處理[13]。首先從經過預處理的孢子圖像中任意選擇4個對象作為初始聚類中心[14]；余下孢子則根據它們與這些聚類中心的相似度，分別分配給與其最相似的聚類；然后計算每個所獲新聚類的聚類中心；不斷重復這一過程直到標準測度函數收斂為止[15]。

經過重復聚類10次后，對圖2(a)的粘連孢子的分割結果如圖3(a)所示。由圖3(a)可以看出，經過K-means聚類的孢子圖像孢子緊湊性較好，可較好地將孢子從復雜的背景中分離出來，為孢子的特征提取奠定了基礎。對經過K-means聚類算法后的粘連孢子邊緣提取與角點檢測，如圖3(b)、圖3(c)所示。(c)是對(b)進行角點檢測并放大后的圖像，圖中的深色區域均為角點檢測的結果。可以發現，由于粘連孢子邊緣不夠平滑，檢測到的偽角點過多，無法利用其進行孢子的計數，尚需進一步對孢子圖像邊緣進行平滑處理以去除偽角點對目標計數的影響。

圖3　K-means算法圖像聚類結果

3) 基于優選傅里葉描述子的粘連孢子邊緣提取經過K-means算法聚類后，在圖像邊界處圖像的灰度值變化比較劇烈，所提取到的偽角點數量偏多，本文采用傅里葉描述子對圖像邊緣進行平滑以解決偽角點數目過多的問題。

傅里葉描述子的基本思想是：在xy平面的一個由K個像素點組成的數字邊界內，從任一點(x0,y0)開始，以逆時針方向在該邊界上行進時，會遇到坐標對：

((x0,y0),(x1,y1),…,(xK-1,yK-1))

(1)

該坐標也可以表示為x(k)=xk和y(k)=yk的形式，并用坐標序列描述圖像邊界得到：

s(k)=[x(k),y(k)]k=0,1,…,K-1

(2)

將每個坐標對可當做一個復數來處理，即s(k)=i(k)+j·y(k)。序列s(k)的離散傅里葉變換(DFT)可以寫成：

(3)

式中：復系數a(u)稱為邊界的傅里葉描述子。

通過對傅里葉描述子系數的傅里葉反變換可以重建圖像邊界s(k)，即：

(4)

假設在計算反變換時，不使用所有的傅里葉描述子系數，而只使用前P(P≤K)個系數。這相當于令上面函數中的a(u)=0(u>P-1)。所得結果是s(k)的如下近似值：

(5)

由式(5)可以看出，對于原始輪廓進行傅里葉描述的關鍵就是確定一個合適的參數P，在能夠表達原始輪廓的前提下得到盡可能平滑的輪廓[16]。對原始孢子輪廓進行一維傅里葉變換所得到的頻譜分布如圖4所示。由圖4可見其頻譜大部分區域的能量相對較低，說明此處表達的是圖像邊緣中的高頻信息，對于圖像概貌的表達能力有限，因此可以對其頻譜圖像進行擬合，以剔除這些能量較小的區域。由于圖像頻譜大致呈高斯分布，可以采用高斯擬合的方式對孢子圖像頻譜曲線進行擬合。

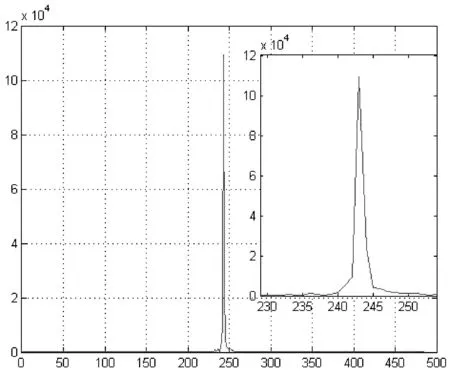
圖4　頻譜分布圖像

4) 傅里葉描述子個數優選方法由式(5)可知，高頻分量決定細節部分，低頻分量決定圖像概貌。隨著P的減小，邊界細節的丟失就會增加，從而得到更為平滑的輪廓。分別令P為240、96、48、24、12和6，得到的圖像輪廓結果如圖5所示。圖5(a)、(b)使用240個、96個傅里葉描述子顯示了圖像原始邊界的緊密對應，圖5(c)、(d)使用相對較少的傅里葉描述子生成的圖像顯示的邊界稍微平滑一些，且基本形狀與原始形狀十分接近。圖5(e)、(f)顯示了無法接受的失真，喪失了邊界的主要特征。優選傅里葉描述子個數描繪孢子邊緣，既要保留粘連孢子的主要特征，又要保證邊緣相對平滑，用于描述圖像特征最優。

圖5　不同傅里葉描述子個數對孢子邊緣的描述

為了優選出適合進行孢子分割的圖像輪廓，對頻譜曲線采用高斯擬合的方式進行擬合，擬合公式如式(6)所示：

f(x)=a1×exp(-((x-b1)/c1)2)

(6)

式中：x為待擬合頻譜的序號;f(x)為頻譜的幅度;a1、b1、c1均為待擬合系數。當擬合結果的殘差平方和SSR 越接近于0，R2-square越接近1，則表明擬合曲線對原曲線f(x)的解釋能力越強，擬合結果越好。根據不同階次擬合誤差分析結果如表1所示，可見當使用5階高斯擬合時綜合誤差相對較小。因此，本文利用采用5階高斯擬合方式對圖4中的放大區域進行擬合，結果如圖6所示。

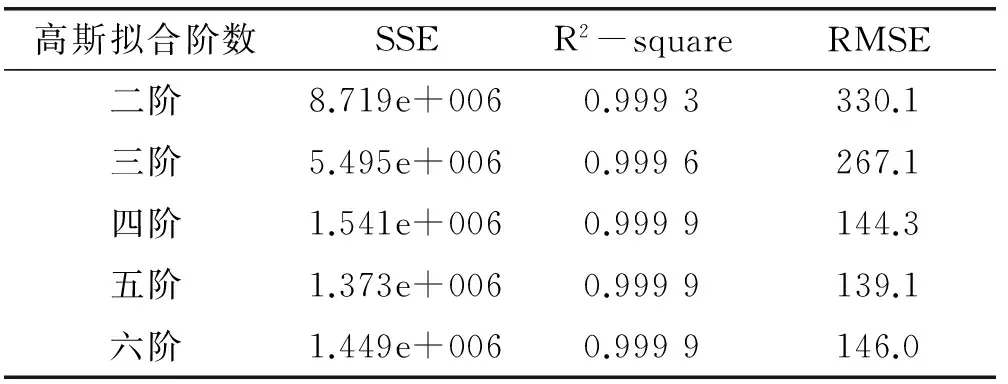
表1　不同階次高斯擬合誤差對比

圖6　五階高斯擬合曲線

由頻譜擬合曲線可知，圖像頻譜幅值在[230,258]區間內頻率幅值顯著，采用28個傅里葉描述子對孢子邊緣進行描述效果較優。對K-means聚類后的孢子圖像使用28個傅里葉描述子提取孢子圖像邊緣，效果如圖7所示。可見，采用28個傅里葉描述子提取到的孢子邊緣相對更加平滑，并且保留了孢子圖像各方面的基本特性，為更精準地提取孢子角點做好準備。

圖7　傅里葉描述子對孢子圖像邊緣提取

1.2.2角點檢測

1) 邊緣跟蹤對于粘連孢子目標，粘連位置存在較為明顯的角點，可以用來進行粘連目標的分割。為了得到連通輪廓的角點，首先對孢子輪廓進行編碼獲取邊界序列[17]。

2) 質心-邊緣點距計算在輪廓編碼算法后即可計算輪廓與質心點之間的距離。對于一個給定的圖像質心點C(x0,y0)和編碼的輪廓矢量V(x1,y1,x2,y2,…,xN,yN,),其中N是輪廓點的數量，點C(x0,y0)和輪廓點之間的距離計算如下所示[18]：

(7)

以三角形輪廓為例，圖8(a)顯示了閉合輪廓，其中M是圖像的質心點，在圖8(b)顯示了閉合輪廓質心點M和輪廓之間的距離。對于一個給定的質心點M，輪廓編碼順序為：A-B-C-A，距離的變化從一個較長的距離d1變化到較短的距離d2，然后從距離d2變化到較長的距離d3，并形成了質心-輪廓距離曲線的極值點，如圖8(c)所示。通過計算距離曲線的極值點的個數來快速求出候選邊角的指數，并通過移除一些曲率極小的偽點來實現頂點的檢測。

圖8　輪廓角點檢測的示意圖

根據質心-邊緣點距離變化判斷角點的關鍵是中心點M的選擇，當孢子的質心落在其邊緣上(如圖9(a)質心點A所示)時，不能提取到孢子的全部角點，并存在偽角點(如圖9(b)所示)，則質心-邊緣距離變化曲線無效。

圖9　孢子角點檢測圖像

對質心在邊緣上的孢子輪廓，通過選擇不同的“中心點”得到的孢子質心-邊緣距離曲線如圖10所示。圖10(b)是孢子通過質心-邊緣距離算法檢測到的角點示意圖。經過該點對孢子輪廓的角點檢測結果與圖9(b)進行對比，可知該中心點所檢測到的角點更為準確。

圖10　中心點孢子角點檢測圖像

2　實驗結果與分析

為了驗證本研究結果的正確性，采用20幅粘連孢子的圖像進行本文算法的處理，并將其中4幅經過傅里葉描述子處理的孢子圖像所提取到的邊緣與圖像原始邊緣進行了對比，結果如圖11(b)、(c)所示。可見傅里葉描述子對邊緣的提取更加平滑，而且還可以剔除邊緣上的毛刺，使孢子邊緣更加清晰，便于對孢子計數。利用質心(中心)-邊緣距離變化檢測孢子圖像角點，對比兩種邊緣提取方式下的角點個數，結果如圖11(d)、(e)所示。從組圖中A點可見，在原始邊緣中，邊緣曲線不夠平滑，會提取到一些偽角點，而經過傅里葉描述子提取到的邊緣不僅使邊緣曲線相對平滑，還保留了孢子圖像基本特征，可以精準地提取到孢子圖像的角點，區分孢子個數。

對20幅孢子圖像頻譜擬合，采用優選傅里葉描述子個數對孢子邊緣進行提取，并進行角點檢測，結果如表2所示。采用傅里葉描述子提取邊緣比原始邊緣對角點的檢測效果更優，總體準確率高達96.2%。由此可見，經過傅里葉描述子提取的邊緣角點檢測更加精準，可以為圖像之后的特征識別、孢子計數提供較好的基礎。

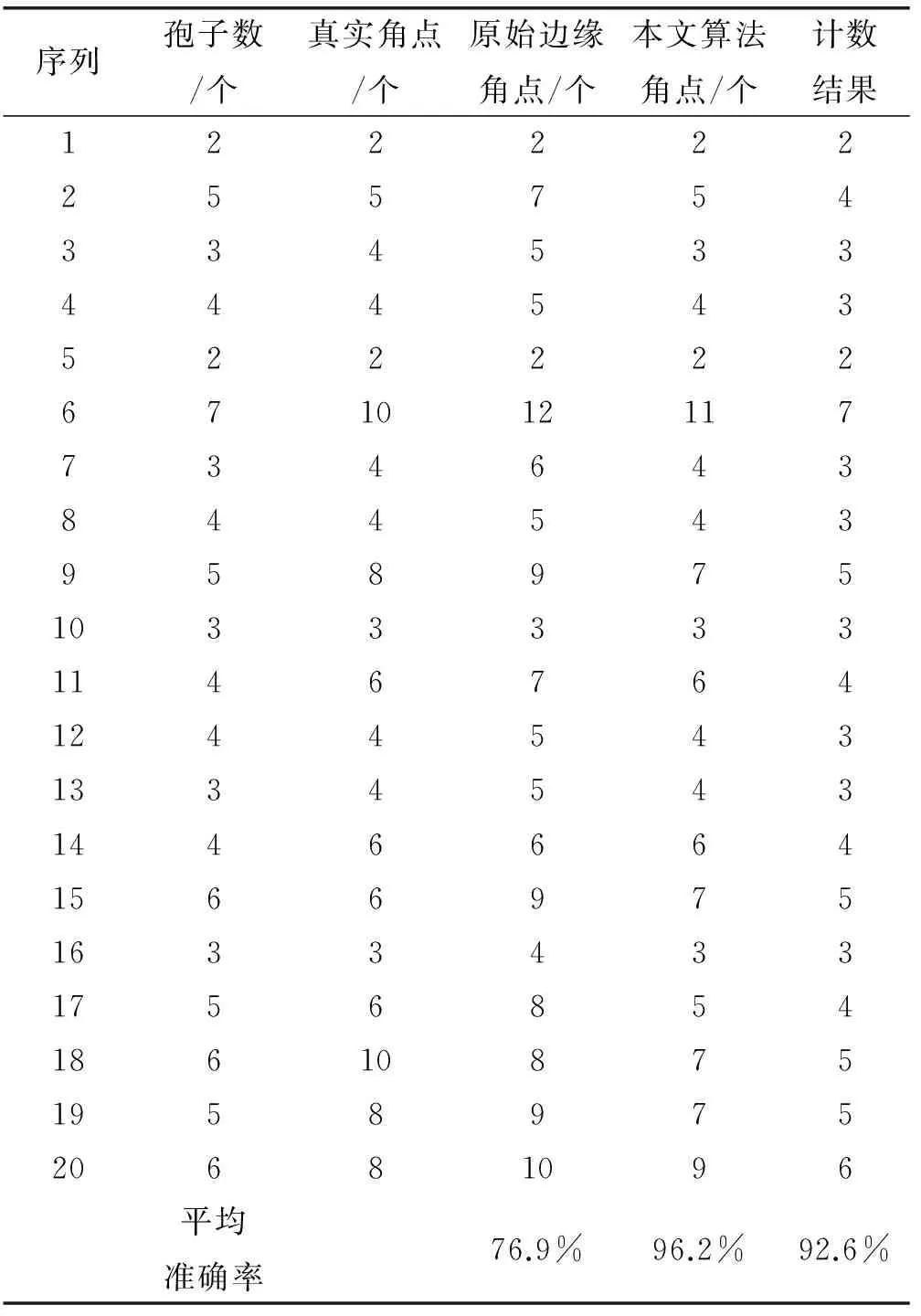
表2　不同邊緣提取對角點檢測的影響

3　結　語

粘連孢子的準確分割是小麥條銹病孢子準確計數的關鍵，為了實現其準確分割，本文結合K-means聚類算法與傅里葉描述子優選方法，較好地實現了粘連孢子的準確分割，所取得的主要結論如下：

(1) 結合K-means聚類算法與優選傅里葉描述子技術，可以較好地實現復雜背景下目標的準確分離。通過優選傅里葉描述子，可以獲得更為平滑的目標輪廓，為準確地確定粘連孢子的角點奠定了基礎。

(2) 為了解決現有角點檢測技術存在偽角點的問題，采用基于距離測度的角點檢測技術，可以較好地去除偽角點的影響。實驗結果表明，利用該方法進行粘連孢子角點檢測的準確率可達96.2%。

[1] 萬安民,趙中華,吳立人.2002年我國小麥條銹病發生回顧[J].植物保護,2003(29):5-8.

[2] 劉曉婉.基于幾何特征的雨滴譜粘連顆粒圖像的快速分割算法[J].科技資訊,2016(14):179-180.

[3] 葛亮,于卡.改進的模板匹配顯微細胞圖像分割算法[J].計算機與現代化,2015(8):1-7,12.

[4] 林小竹,王彥敏,杜天蒼,等.基于分水嶺變換的目標圖像的分割與計數方法[J].計算機工程,2006(32):181-183.

[5] 梁光明,孫即祥.一種基于數學形態學的多結構元圖像分割算法[J].計算機工程與應用,2007(43):70-72.

[6] Danielis A,Giorgi D,Larsson M,et al.Lip segmentation based on Lambertian shadings and morphological operators for hyper-spectral images[J].Pattern Recognition,2017,63:355-370.

[7] 繆慧司,梁光明,劉任任,等.結合距離變換與邊緣梯度的分水嶺血細胞分割[J].中國圖象圖形學報,2016(21):192-198.

[8] 楊信廷,孫文娟,李明,等.基于K均值聚類和開閉交替濾波的黃瓜葉片水滴熒光圖像分割[J].農業工程學報,2016(32):136-143.

[9] Bao S,Chung A C S.Feature Sensitive Label Fusion with Random Walker for Atlas-based Image Segmentation[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2017,26(6):2797.

[10] 陳浩,王景中,姚光明.基于類圓分割的棒材計數圖像識別[J].工程圖學學報,2004(25):98-103.

[11] 宋懷波,張傳棟,潘景朋,等.基于凸殼的重疊蘋果目標分割與重建算法[J].農業工程學報,2013(3):163-168.

[12] 鄧仕超,黃寅.二值圖像膨脹腐蝕的快速算法[J].計算機工程與應用,2017(53):207-211.

[13] 汪中,劉貴全,陳恩紅.一種優化初始中心點的K-means算法[J].模式識別與人工智能,2009(22):299-304.

[14] 楊善林,李永森,胡笑旋,等.K-means算法中的k值優化問題研究[J].系統工程理論與實踐,2006(26):97-101.

[15] Gan G,Ng K P.k-means clustering with outlier removal[J].Pattern Recognition Letters,2017,90(C):8-14.

[16] 趙三琴,劉德營,丁為民,等.邊界點數量對傅里葉描述子識別精度的影響[J].農業機械學報,2014(45):305-310.

[17] Gheorghiu E,Kingdom F A A,Sull M,et al.Curvature coding in illusory contours[J].Vision Research,2009,49(20):2518-2530.

[18] Hasim A,Herdiyeni Y,Douady S.Leaf shape recognition using Centroid Contour Distance[J].IOP Conference Series:Earth and Environmental Science,2016,31(1):012002.