基于BP神經網絡和改進D-S證據理論的目標識別方法

張　志　楊清海

(西安電子科技大學通信工程學院綜合業務網理論及關鍵技術國家重點實驗室　陜西 西安 710070)

0　引　言

D-S證據理論具有很強的處理不確定信息能力，表現出很好的工程實用性，因而成為信息融合的經典算法，多用于多傳感器目標識別領域[1-3]。在應用經典D-S證據理論時，其關鍵參數基本概率賦值的獲取往往憑經驗公式或用統計方法得出，主觀性較大，導致決策的可信度低。文獻[4]提出了利用統計證據和利用目標速度與加速度等方法獲得基本概率賦值，其中統計證據理論的應用要基于觀測值應決定一個似真函數和焦元都是嵌套的假設，應用條件較理想化。利用目標速度和加速度來獲取基本概率賦值，對實際運動目標而言具有很高的概率偶然性。文獻[5]提出了結合粗糙集理論，定義規則強度和決策擴充規則，基于決策表的基本概率賦值方法。其方法先對初始歷史數據作離散化預處理，再根據定義規則進行計算，但計算復雜度高，效率較低。為此，本文提出利用BP神經網絡[6-8]獲取基本概率賦值。BP神經網絡具有很強的自組織、自學習和非線性映射能力及良好的容錯性和魯棒性。且經過訓練的BP神經網絡具有良好的泛化能力。本文通過紅外成像傳感器采集到的目標特征數據來訓練BP神經網絡獲取基本概率賦值具有工程實際意義和準確性。

經典D-S證據理論在合成高沖突度證據時，往往會出現與常識推理相悖的情況。為了解決這一問題，學者們提出了各種修正方案,典型的有Yager方法[9]、Murphy方法[10]、李弼程方法[11]等。文獻[9]中，Yager提出將證據的沖突部分全部賦給未知命題，去除了Dempster-Shafer歸一化過程，此方法雖然能合成高沖突度證據，但完全否定了沖突證據的作用。文獻[10]中,Murphy提出先對初始證據集進行算術平均，再利用D-S證據理論。該方法能有效融合高沖突度證據，但是忽略了各條證據間的關聯性。文獻[11]中，李弼程等將沖突概率按各個命題的平均支持程度加權后再進行分配，也能克服經典D-S證據理論在合成高沖突證據時存在的局限性，但該合成方法較保守，收斂速度慢。

本文考慮到證據之間的關聯性，提出了證據信任因子的概念。參照文獻[12-13]引入Jousselme距離,先計算n條證據任意兩條證據之間的Jousselme距離，然后計算證據Ei到證據集E的歐式距離，進而根據定義計算此證據的信任因子。通過歸一化信任因子得到證據的權重，再對修正的證據進行加權平均得到期望證據，最后對期望證據進行n-1次融合。實驗結果表明，BP神經網絡和本文改進的D-S證據理論相結合，能更準確地進行目標識別。

1　目標識別系統模型

在進行目標識別的場景下，單個傳感器獲取的信息往往是對待識目標的不完整描述，利用多傳感器進行信息提取，能夠降低信息的不確定性，增強互補性。為此,本文提出了如圖1所示的識別系統模型。該模型由基本概率賦值獲取和改進證據理論的目標識別兩部分組成。利用多組紅外成像傳感器[14]對待識別目標進行屬性信息的采集，提取出特征向量。將采集數據按特征向量劃分訓練數據和測試數據，訓練數據用于BP神經網絡模型的構建，測試數據經由BP神經網絡的輸出，歸一化后作為證據的基本概率賦值。然后利用改進的D-S證據理論進行融合目標識別。該模型不僅充分利用了BP神經網絡強大的自組織、自學習和非線性映射能力，解決了基本概率賦值難以獲取的問題。而且將改進的D-S證據理處理不確定性信息和高沖突度證據的優勢發揮了出來，從而提高了目標識別精度。

圖1　系統模型框圖

2　神經經網絡獲取基本概率賦值

2.1　 構建BP神經網絡組

BP神經網絡，是一種利用誤差反向傳播訓練算法的多層前饋網絡。為了提高了基本概率賦值的準確性，本文將構建m組BP神經網絡。對于每一組BP神經網絡而言，參數設置方法如下：

(1) BP神經網絡具有強大的非線性映射能力，且任意非線性連續函數都可用三層網絡來反映，一般選取一個輸入層，一個隱含層，一個輸出層的三層結構。

(2) 輸入層的神經元個數為特征向量元素的個數；輸出層的節點數為待識目標的數目；隱含層的節點數可得出，公式如下：

(1)

傳遞函數可以抑制邊緣奇異性較大的數據，約束輸出值范圍。一般選取sigmiod型傳遞函數，其收斂速度快，同時控制輸出值在0～1之間。

(3) 最大訓練次數和誤差精度作為網絡訓練停止的條件，按照實際需要來設定。

2.2　獲取基本概率賦值

設構建m組BP神經網絡，有k個待識目標。測試樣本經由BP神經網絡組得到m組k個[0,1]之間的數值，將每一個BP網絡所得的數值歸一化處理，即得到該條證據對該命題的基本概率賦值。

歸一化過程：

(2)

Vi=(aik,…,ai2,ai1)T

(3)

(4)

3　改進D-S證據理論目標識別

利用BP神經網絡組獲取基本概率賦值之后，我們需要根據改進D-S證據理論對其進行合成，合成結果是目標識別的依據。

3.1　 Dempster-Shafer(D-S)組合規則

3.2　 改進的證據理論

研究發現，使用經典的D-S證據理論進行證據合成時，可能出現1信任悖論、0信任悖論、“一票否決”等與主觀常識相悖的結果。因此經典D-S證據理論的使用范圍具有一定的局限性。為了避免上述問題，本文提出了證據信任因子的概念，按照信任因子的大小賦予證據不同的權重，得到期望證據。其核心思想是，根據證據與證據集的歐式距離，得到該證據的沖突度。高沖突度的證據，信任因子小，賦予的權重系數也小。相反，信任因子大，權重系數也大，加權平均后得到期望證據。這樣就消減了高沖突度證據對合成結果的影響。

3.2.1證據沖突度的衡量方法

若識別框架U={θ1,θ2,…,θn}，下有E1和E2兩個證據，對應的基本概率賦值為m1和m2，焦元分別為A和B，則證據E1和E2兩個證據之間的Jousselme距離：

(6)

D為2n×2n的正定矩陣，矩陣中的元素：

(7)

式中：D(A,B)稱為Jaccard系數，反映了焦元A和B間相似性。

d(m1,m2)的具體計算式如下：

(8)

式中：=‖m1‖2；=‖m2‖2；為兩個向量的內積,表達式為：

假設有n個證據，利用式(7)、式(8)可定義證據距離矩陣Dn×n：

定義證據Ei到證據集E的歐式距離：

(9)

式中：Si是衡量證據Ei沖突度大小的指標，反映了該證據與其他證據的差異程度。當Si較小時，說明Ei與其他證據較一致，沖突度低。相反，Si較大時，說明Ei同其他證據存在較大的差異，該證據歧異性大，沖突度高。

3.2.2證據信任因子Crd的計算

沖突度低的證據，與其他證據的差異性小，可信度高，此時Si→0，Crdi→1，且Crdi隨著Si的增大緩慢減小。相反，高沖突證據的可信度低，則Si→1，Crdi→0，且Crdi隨著Si的增大迅速趨于0。可見信任因子Crdi與證據的歐式距離Si之間負相關且符合指數函數關系。可假設：

Crdi=f(Si)=(1-Si)α-Si

(10)

對其求導：f′(Si)=(Silnα-lnα-1)α-Si

要保證f(Si)在Si∈[0,1)時是減函數，則需要f′(Si)<0即：

f′(Si)=(Silnα-lnα-1)α-Si<0得到α≥e-1。

如圖2所示，對α取不同的值，通過MATLAB仿真，觀察f(Si)曲線的變化趨勢，當α=e-1時，最符合f(Si)的性質。

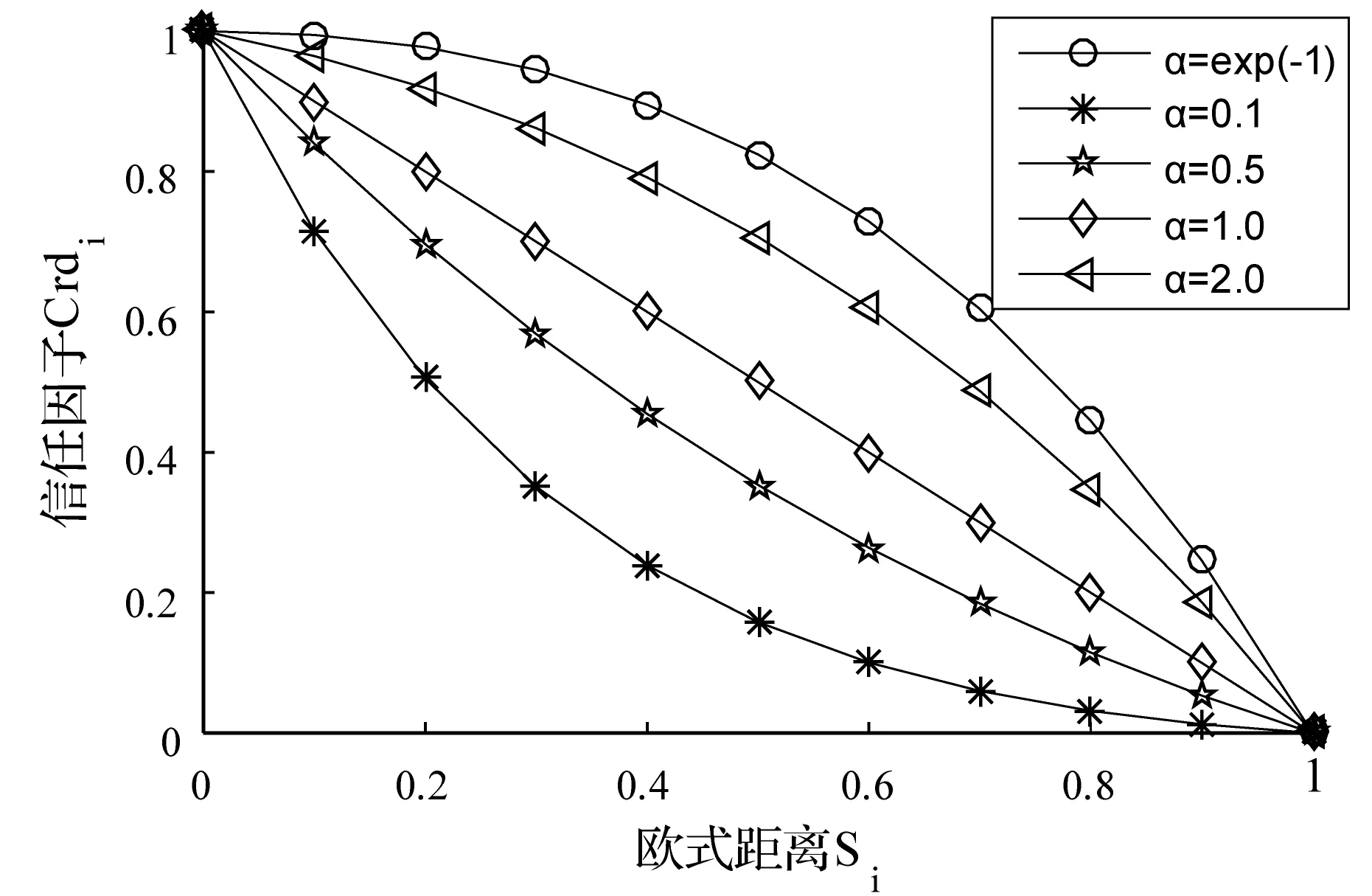
圖2　信任因子與歐式距離關系曲線

取α=e-1，則

Crdi=f(Si)=(1-Si)e-SiCrdi∈(0,1]

(11)

3.2.3期望證據的合成

在得到證據Ei的信任因子Crdi之后，進一步獲得此證據被其他證據的支持度，并將該支持度作為此證據的權重ωi，計算式為：

Crdmax=max(Crd1，Crd2，…，Crdn)

(12)

(13)

得到證據的權重系數向量為：

W=[ω1,…,ωi,…,ωn]

(14)

對n條證據加權平均后，得到期望證據：

(15)

利用D-S證據理論對期望證據M迭代組合n-1次后的結果作為n條證據的合成結果。

3.2.4目標判決準則

本文采用以下準則進行最終目標判決：

(1) 最終判決的目標具有最大的基本概率賦值。

(2) 最終判決的目標與其他目標的基本概率賦值之差要大于設定的閾值ε1。

(3) 不確定基本概率賦值m(Θ)必須小于設定的門限ε2，其中Θ為不確定集合。

(4) 最終判決的目標的基本概率賦值要大于不確定基本概率賦值m(Θ)。

4　實例仿真及結果分析

4.1　紅外成像傳感器采集目標屬性信息

本文采用四組(S1,S2,S3,S4)紅外成像傳感器對三個目標(攻擊艦、輔助艦、指揮艦)進行9種屬性信息的采集。分別采集22組屬性數據，一共88組數據。表1是攻擊艦(O1)、輔助艦(O2)、指揮艦(O3)的紅外樣板特征值。

表1　紅外樣板特征值

4.2　神經網絡組的構建

本文將88組數據樣本進行劃分，前84組作為訓練樣本，其中85、86、87、88組數據作為測試樣本。測試樣本數據如表2所示。

表2　測試樣本特征值

注:O1代表攻擊艦，O2代表輔助艦，O3代表指揮艦

將84組訓練樣本的9個特征參數分成四組分別訓練BP神經網絡，得到BP神經網絡組。將測試樣本也以同樣的方式分組，輸入訓練好的神經網絡，獲得的輸出作為D-S證據理論的證據進行下一步的合成。

建立的BP神經網絡分別為:

NN1、NN2、NN3、NN4。

第一組的輸入向量：

(A,AT,α,β,EA,P,Rαβ)T。

第二組的輸入向量：

(AT,α,β,EA,P,Rαβ,I1)T。

第三組的輸入向量：

(A,AT,α,β,EA,P,Rαβ,I1)T。

第四組的輸入向量：

(AT,α,β,EA,P,Rαβ,I1,I2)T。

網絡的輸出，設定為三種：

(1,0,0)T、(0,1,0)T、(0,0,1)T。這三個輸出向量分別表示目標O1(攻擊艦)、目標O2(輔助艦)、目標O3(指揮艦)。

本文構建只包含一個輸入層、一個隱含層和一個輸出層的三層網絡模型。NN1、NN2、NN3、NN4中輸入層的神經元個數分別是7、7、8、8，輸出層的節點數都為3，隱含層的節點數都為13(取α=10)。設置的最大訓練次數為5 000，誤差精度為10-2，傳遞函數為tansig。

將84組訓練樣本分別輸入神經網絡組，得到的訓練誤差曲線分別如圖3-圖6所示。

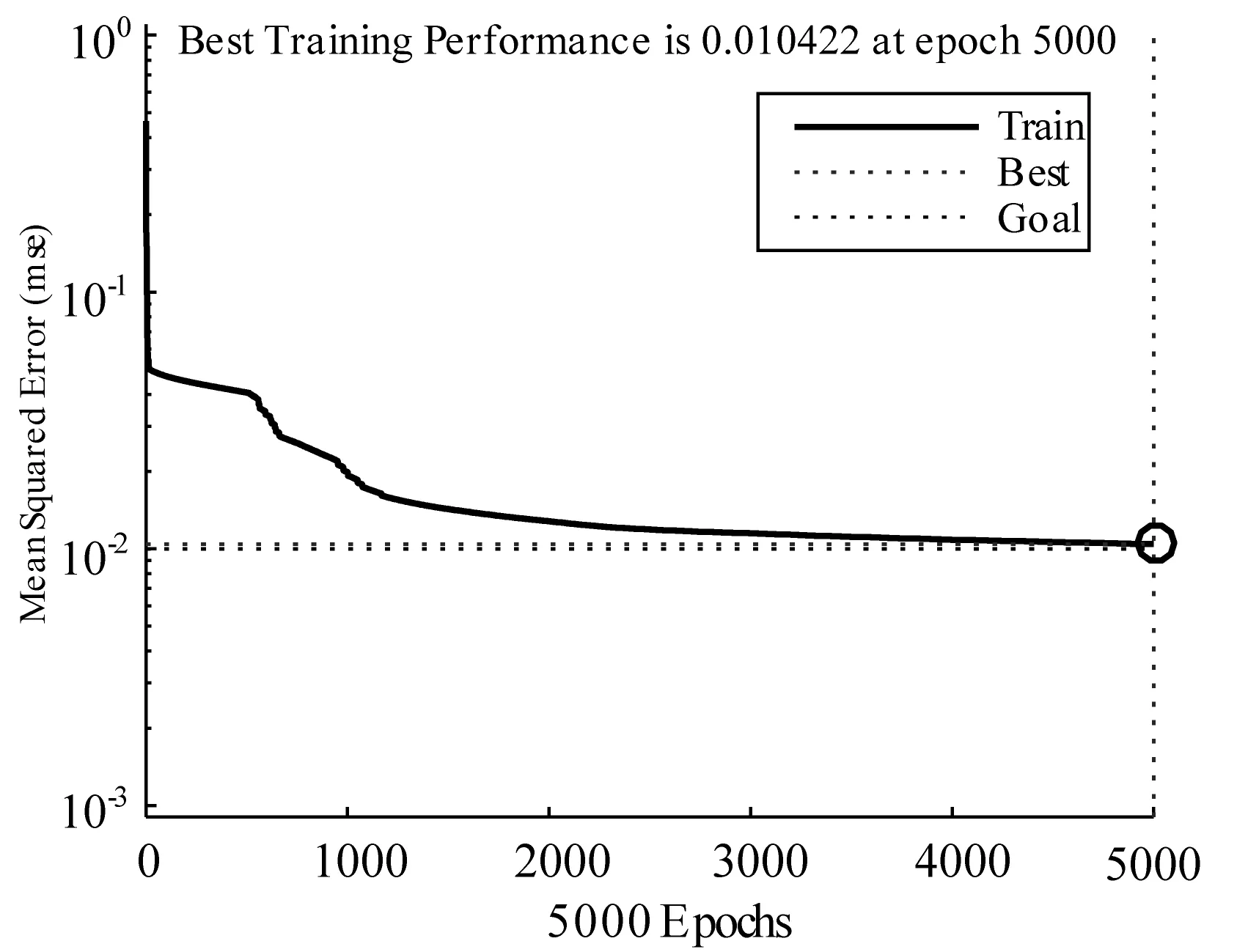
圖3　神經網絡NN1誤差變化曲線

圖4　神經網絡NN2誤差變化曲線

圖5　神經網絡NN3誤差變化曲線

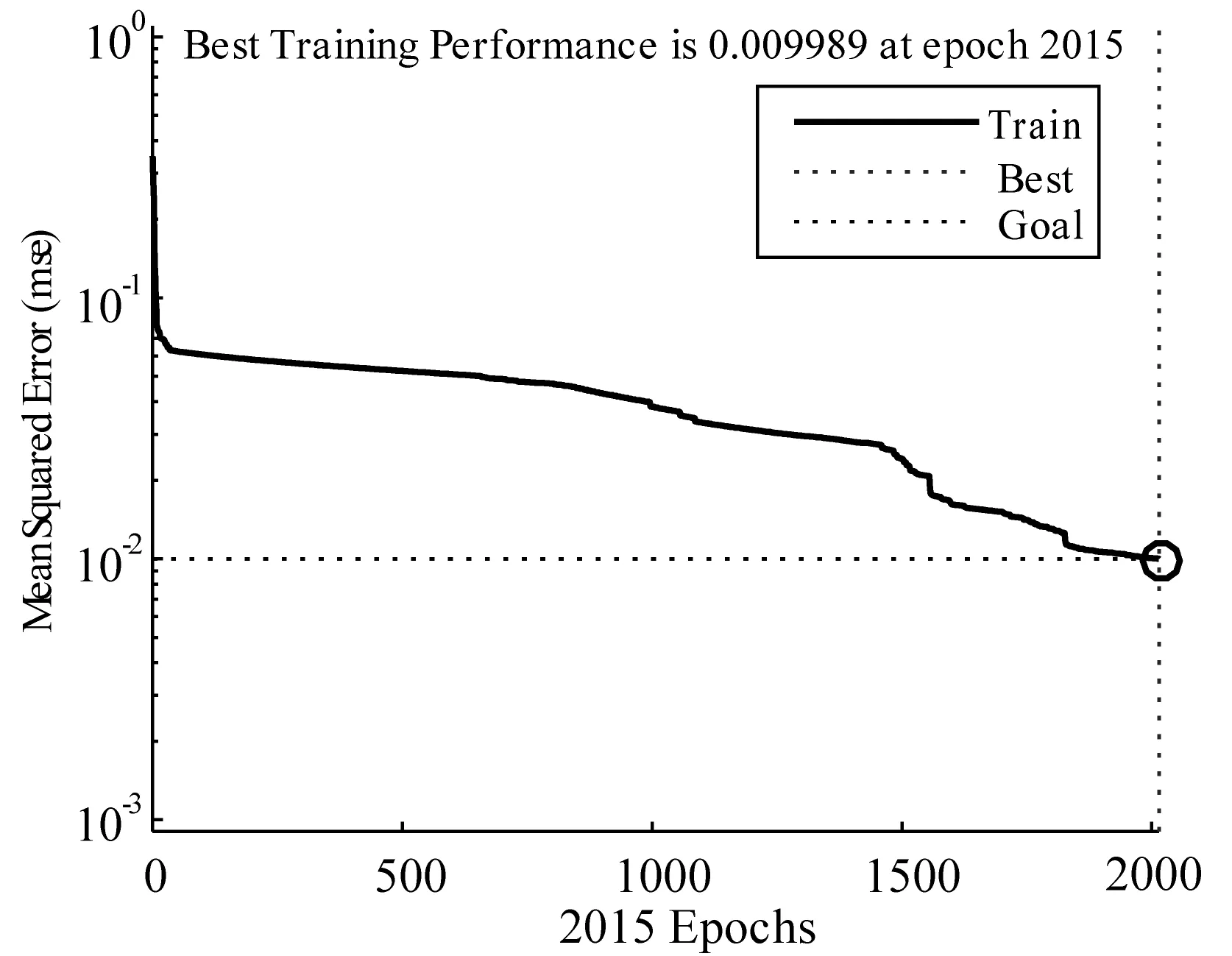
圖6　神經網絡NN4誤差變化曲線

4.3　基本概率賦值的獲取

測試樣本經由4組BP神經網絡得到4組3個[0,1]之間的數值，將每一個BP網絡所得的數值歸一化處理，即得到該條證據對該命題的基本概率賦值。

4.4　證據合成及對比結果分析

為了說明本文方法的有效性和改進效果，下面對上文中獲取的基本概率賦值分別采用經典D-S證據理論合成方法、Yager算法、Murphy算法和本文的改進算法進行證據組合。并對融合結果做比較分析。測試樣本經由4種不同算法融合結果，如表3-表6所示。

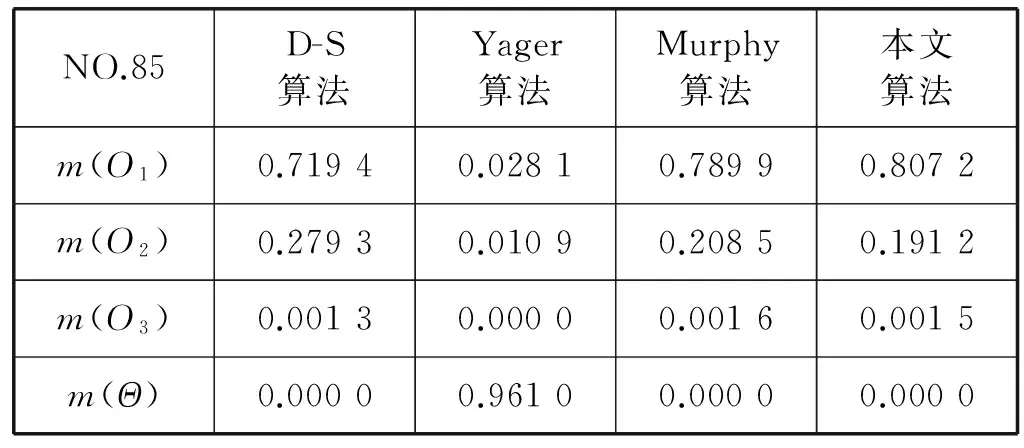
表3　樣本85經由四種算法合成結果

表4　樣本86經由四種算法合成結果

表5　樣本87經由四種算法合成結果

表6　樣本88經由四種算法合成結果

4.5　識別結果

若取門限值ε1=0.05，ε2=0.7，根據目標判決準則可以得到四種不同算法的識別結果如表7所示。

表7　四種算法識別結果

注:O1代表攻擊艦，O2代表輔助艦，O3代表指揮艦

4.6　結果分析

對于85號和87號測試樣本，D-S經典算法、Murphy算法、本文算法都能做出準確目標識別，且本文算法精度最高。而對于86號和88號測試樣本，D-S經典算法都做了誤判，究其原因，當證據之間高度沖突時，特別是出現了基本概率賦值趨于0的證據，即使后面的證據高度支持此命題，但依據D-S經典合成公式，此命題的概率依然會很小，甚至一直為0。對于Yager算法，由于其不確定命題的基本概率賦值m(Θ)都大于給定的ε2=0.7，因此識別結果都是無法判斷。這是因為Yager將支持沖突的基本概率賦值完全歸入未知領域，我們無法做出判斷。由表7可以看出，Murphy算法和本文算法4次都能做出正確的目標識別，不過結合表3-表6，可以看到本文算法的識別精度都是高于Murphy算法。這是因為Murphy算法僅是對證據進行簡單的算術平均，忽略了證據之間的關聯性。本文算法，考慮到了證據之間的關聯性，提出了信任因子的概念，而且依據嚴謹的數學推理給出了信任因子的表達式。根據信任因子賦予每條證據相應的權值，再結合D-S公式進行證據合成，因而其識別結果具有更高的準確度。

5　結　語

本文采用BP神經網絡，有效解決了基本概率賦值難以獲取的問題，且獲取過程更符合實際場景。同時，改進的D-S證據理論不僅解決了高沖突度證據的合成問題，而且較其他改進算法有更高的目標識別精度，從而證明了BP神經網絡和改進D-S證據理論的結合方法在目標識別應用中的有效性。

[1] Li Y, Chen J, Ye F, et al. The Improvement of DS Evidence Theory and Its Application in IR/MMW Target Recognition[J]. Journal of Sensors, 2016(6):1-15.

[2] Wang P, Shang C X, Han Z Z. Target identification based on evidence theory of improved basic probability assignment[M]// Electronics, Communications and Networks IV.2015:1171-1175.

[3] 王力，白靜. 改進的證據理論在多傳感器目標識別中應用[J]. 科技通報, 2016, 32(7):134-137.

[4] 孫銳, 孫上媛, 葛云峰. 基于D-S證據理論的基本概率賦值的獲取[J]. 現代機械, 2006(4):22-23.

[5] 路艷麗, 雷英杰, 李兆淵. 一種D-S證據推理的BPA獲取方法[J]. 空軍工程大學學報(自然科學版), 2007, 8(3):39-42.

[6] Huang D Z, Gong R X, Gong S. Prediction of Wind Power by Chaos and BP Artificial Neural Networks Approach Based on Genetic Algorithm[J]. Journal of Electrical Engineering & Technology, 2015, 10(1):41-46.

[7] 吳春華，馮夏云，袁同浩，等. 基于BP神經網絡的光伏故障電弧檢測方法研究[J]. 太陽能學報, 2016, 37(11):2958-2964.

[8] Wu B, Han S, Xiao J, et al. Error compensation based on BP neural network for airborne laser ranging[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(8):4083-4088.

[9] Yager R R. General approach to the fusion of imprecise information[J]. International Journal of Intelligent Systems, 1997, 12(1): 1-29.

[10] Murphy C K. Combining belief functions when evidence conflicts[J]. Decision Support Systems, 2000, 29(1):1-9.

[11] 李弼程，王波，魏俊，等.一種有效的證據理論合成公式[J].數據采集與處理,2002,17(1):33-36.

[12] Han D, Dezert J, Yang Y. New Distance Measures of Evidence Based on Belief Intervals[C]// International Conference on Belief Functions. Springer International Publishing, 2014:432-441.

[13] Wang H, Li W, Qian X, et al. An Improved Jousselme Evidence Distance[M]// Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems. Springer Singapore, 2016.

[14] 張旭艷，華宇寧，董曄，等.一種基于不變矩的紅外目標識別算法[J]. 沈陽理工大學學報, 2016, 35(2):10-13.