量子粒子群算法在WSN三維定位中的研究
劉 小 園
(羅定職業技術學院 廣東 羅定 527200)
0 引 言
無線傳感網絡定位算法有基于測距的三邊測量法、三角測量法、極大似然估計法和基于非測距的DV-HoP算法、質心算法、近似三角形內點測試法等,這類算法主要針對二維區域節點定位。在實際工程應用中,傳感節點往往隨機空投至三維空間,如森林,海洋,高山等。如何在立體空間實現對傳感節點的精確定位是目前研究的熱點和重點[1]。
Emmons提出一種3D-DVHoP算法,其原理與傳統DV-HoP算法相似。首先利用最短通路計算三維區域中各錨節點之間最小跳數,再根據實際距離計算平均每跳長度,將實際跳數與平均跳距相乘得到與附近錨節點之間距離,最后利用四邊測量或極大似然估計法計算節點三維坐標。
3D-DVHoP算法將傳統的二維區域拓展至立體空間,為節點三維定位提出算法模型。其和傳統DV-HoP算法類似,根據網絡連通情況使用跳數作為參考距離,實現簡單,硬件成本較低,能很好地兼容現有設備。但其定位精度依賴于具體的網絡拓撲,當錨節點分布不均時會產生較大定位偏差。因為在三維空間中,非相鄰錨節點之間通路并非直線,通過相鄰節點之間接力會導致“繞彎”現象[2],再利用兩點彎線跳段替代直通距離勢必帶來定位偏差,并且在三維空間中表現更為明顯。如圖1所示。

圖1 “繞彎”現象示意圖
由于節點繞彎現象無法避免[3-4],為提高定位精度,業界提出各類改進的3D-DVHoP算法,如基于多重共線性的三維DVHoP定位算法[5]、基于加權的三維DVHoP算法[6]、基于粒子群優化的三維DVHoP算法等[7],但這類優化算法都容易陷入局部最優解現象[8],定位精度雖有提高,但在25th、50th和70th定位偏差均在3%以上[9],難以滿足工程應用需求。
有鑒于此,本文提出一種基于量子粒子群改進算法。在尋找鄰居節點之間的實際距離與繞彎距離最小誤差時,利用3D-DVHoP算法結合量子旋轉門變異規則,計算距離矩陣和跳數矩陣函數評價粒子群個體行為。通過交叉變異修正個體粒子速率和狀態,增加粒子搜索的廣泛性和遍歷性,避免粒子陷入盲目搜索和局部最優, 從而導致算法搜索停滯或提前收斂現象。
1 量子粒子群算法
量子粒子群算法是將量子進化算法融合到粒子群中產生的一種新算法[10]。算法中個體粒子位置通過量子比特進行編碼,利用量子旋轉門更新粒子位置向量和移動速率。在粒子群中,每個粒子代表搜索空間中的每個解。在量子粒子群中,量子旋轉門通過量子粒子移位實現對搜索空間中兩個位置的同時移動。因此一個量子粒子對應于搜索空間中的兩個解,以此釆增加粒子搜索的廣泛性和遍歷性,提高算法優化效率,避免陷入局部最優現象。
2 3D-DVHoP算法原理
3D-DVHoP算法定位過程分為三個階段。第一階段,錨節點向鄰居節點廣播分組信息,包含自身位置坐標、ID以及跳數字段,獲得網路中其他錨節點位置信息和跳數距離,從而估算平均跳離,見式(1):
(1)

第二階段,錨節點將平均跳距加入自身分組信息,再次洪泛至整個網絡,并計算其與所有錨節點之間的參考跳距。
第三階段,根據與其他錨節點的參考距離,利用四邊測量或極大似然估計法計算節點的三維坐標。
在立體空間中,設未知節點M(x,y,z)附近存在n個錨節點,坐標分別為(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn),與節點M之間距離分別d1,d2,…,dn。如圖2所示。
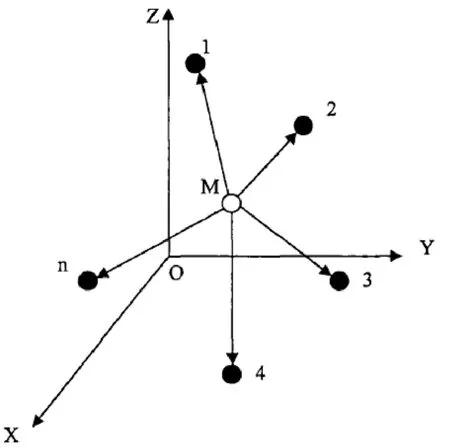
圖2 節點空間拓撲圖
根據式(1)計算未知節點M與其他錨節點之間參考距離:
(2)
將式(2)中方程組每一行分別減去第n行,并改成“AX=b”線性表達式,其中:
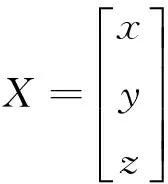
(3)
最后根據最小方差估計法計算節點M三維坐標:
(4)
3 優化算法思想和定位過程
3.1 粒子群優化算法和不足
要尋找目的節點與鄰居錨節點之間實際距離與估算繞彎距離的最小誤差,根據式(4)可以轉換為函數最優化問題。在粒子群算法中,每個粒子位置代表函數優化的每個可行解,粒子根據目標函數修正當前位置和飛行方向,找出全局最優解,完成搜索過程。然而,粒子群算法是一個正向反饋的過程,當局部信息過優時容易產生大量粒子聚集導致算法提早收斂,陷入局部最優的問題。另外,慣性權重W為(0,1)之間隨機數,使得算法早期粒子速度更新沒有規律,后期收斂緩慢。因此利用單純的粒子群優化求解效果不佳,定位精度有待提高。
3.2 建立目標函數
新算法基于3D-DVHoP第三階段獲得的距離矩陣和跳數矩陣,采用量子粒子群算法修正節點估算距離以減少偏差,提高定位精度。為更好地描述量子粒子群算法節點部署,找到實際距離與估算繞彎距離之間的最小誤差,建立優化目標函數為:
(5)
其中,ci是傳感網絡節點路徑成本,C為監測區域部署的傳感器路徑成本。
3.3 算法定位過程
新算法首先對粒子群進行量子編碼,利用量子旋轉門調整個體粒子速率和方向從而確定搜索空間,避免粒子過早收斂造成局部最優。為得到目標函數最優解,需要確定量子旋轉門變異規則和適應度函數(適應度函數是與3D-DVHoP算法中得到的距離矩陣和跳數矩陣相關的函數)以評價粒子群個體行為,得到尋優群體。最后通過粒子群迭代優化尋找到目標函數的最優解,從而修正節點最優坐標值。新算法具體流程如下:
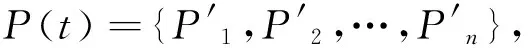
第二步確定粒子位置狀態。在一個n維搜索空間,有m個粒子(表示目標函數的可能解)組成的群體,其中在t時刻第i個粒子位置為:
Xi(t)=?xi,1(t),xi,2(t),…,xi,n(t)」
(6)
在t時刻粒子最好個體位置為:
Pi(t)=?Pi,1(t),Pi,2(t),…,Pi,n(t)」
(7)
整個粒子群最好全局位置為:
G(t)=?G1(t),G2(t),…,Gn(t)」
(8)
第三步對粒子群進行量子化編碼。定義量子比特,其狀態可為:
|τ〉=αij|0〉+βij|1〉
(9)


(10)
其中,αij,βij表示為種群中所有染色體基因。
第四步建立適應度函數評價個體粒子行為狀態。適應度函數值越小,表示適應度越好。適應度評價函數為:
(11)
其中,Dij為傳感網絡中相鄰節點i與j之間真實距離,dij是相鄰節點i與j之間估算的參考距離;djk是相鄰節點j與k之間估算的參考距離。由式(10)得到粒子i最好個體位置為:
(12)
整個粒子群最好全局位置為:
g=argmin{f[Pi(t)]}
G(t)=Pg(t)
(13)
第五步計算個體粒子位置。將粒子個體最佳位置和整個粒子群體最佳全局位置進行比較,從而更新個體粒子位置:
Xi,j(t+1)=pi,j(t)+|Cj(t)-|Xi,j(t)
(14)
其中:
(15)
第六步利用量子旋轉門修正個體粒子速率和狀態,避免陷入局部最優。定義量子旋轉門U(θ),利用量子旋轉門不同旋轉角度對量子染色體實施變異操作,并對個體粒子行為狀態進行修正。令:

(16)
(17)
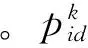
重復第五步和第六步,粒子通過判斷群體最佳全局位置,結合量子旋轉門的變異操作不斷更新當前位置和飛行速率,最終找到全局最優解,完成搜索過程,根據目標函數尋找到未知節點與錨節點之間實際距離與估算繞彎距離的最小誤差。
第七步根據3D-DVHoP算法,利用最小方差計算節點M三維坐標。
3.4 定位偏差評價方式
算法采用平均定位偏差對三維節點定位精度進行評價,公式為:
(18)
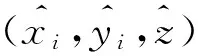
4 仿真測試
4.1 仿真環境
仿真環境采用基于網格節點放置模型,節點在100×100×100三維區域內隨機分布,未知節點數量70,錨節點數量30,節點通信半徑20,初始化粒子群規模200,加速系數c1=1,c2=1,最大迭代次數k=800,利用MATLAB7.0軟件對算法仿真比較。
4.2 三維定位偏差測試
三維空間中新算法與3D-DVHoP經典算法定位偏差見圖3所示。由于錨節點非均勻分布,3D-DVHoP在計算平均跳距時會產生誤差,并且錨節點密度越小,定位偏差越大。圖3中某些區域錨節點密度較低,3D-DVHoP計算的最大偏差高達23.87%。新算法利用量子粒子群尋找實際距離與估算距離之間的最小誤差值,從而修正定位結果,平均定位偏差明顯小于3D-DVHoP算法。
圖3 定位偏差測試圖
4.3 節點密度定位偏差測試
錨節點密度與定位偏差測試結果見圖4所示。所有優化算法定位偏差都隨節點密度增大而減小,滿足共性規律,但當錨節點數量小于40時算法差異明顯。其中3D-DVHoP直接將彎線跳段距離替代直通距離,算法定位偏差最大。基于多重共線性的三維DVHoP定位算法、基于加權的三維DVHoP算法和基于粒子群優化的三維DVHoP算法,采用不同技術修正非相鄰節點之間的“繞彎”誤差,但找到的解并非全局最優解,陷入局部最優問題。新算法平均定位偏差最小,當節點數量大于55時偏差趨于收斂,在25th、50th和70th距離偏差值分別是1.25米、0.6米和0.5米,均在1.5%以內。

圖4 節點密度定位偏差測試圖
5 結 語
3D-DVHoP在三維空間利用彎線跳段距離替代直通距離,因節點“繞彎”現象導致較大定位偏差,已有改進算法在修正偏差時已無法找到全局最優解,或多或少的存在算法提前收斂現象。本文提出一種基于量子粒子群改進算法,通過判斷粒子群體最佳全局位置和量子旋轉門變異操作修正個體粒子速率和狀態,找出節點實際距離與估算繞彎距離之間的最小誤差以提高定位精度,算法相對復雜,但定位結果更為精確。
[1] 曾子維,張超.一種質心與DV-Hop算法相結合的WSN節點定位算法[J].計算機應用與軟件,2015,32(11):130-133.
[2] 劉士興,黃俊杰,劉宏銀,等.基于多通信半徑的加權DV-Hop定位算法[J].傳感技術學報,2015,28(6):883-887.
[3] 涂巧鈴,牟小燕,宋佳.一種改進的DV-Hop改進算法[J].重慶理工大學學報(自然科學版),2014,28(11):84-88.
[4] 高文根,陳其工,江明,等.基于距離補償模型的改進DV-Hop定位算法[J].計算機工程,2015,41(3):32-36.
[5] 劉文遠,王恩爽,陳子軍.無線傳感器網絡中DV-Hop定位算法的改進[J].小型微型計算機系統,2011,32(6):1071-1074.
[6] 陳三風,陳萬明.基于RSSI誤差分析的無線傳感器網絡定位研究[J].計算機工程與應用,2011,47(14):10-12,75.
[7] 沈軍,黃春華,羅護,等.基于RSSI優化的模型參數實時估計定位算法[J].計算機工程與設計,2012,33(2):464-468.
[8] Chen H,Sezaki K,Deng P,et al.An improved DV-Hop localization algorithm with reduced node location error for wireless sensor networks[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer Science,2008,E91-A(8):2232-2236.
[9] Savarese C,Rabaey J M,Langendoen K.Robust Positioning Algorithms for Distributed Ad-Hoc Wireless Sensor Networks[C]//Proceedings of the General Track of the Annual Conference on USENIX Annual Technical Conference,2002:317-327.
[10] Sun G,Qiao G,Xu B.Corrosion monitoring sensor networks with energy harvesting[J].IEEE Sensors Journal,2011,11(6):1476-1477.

