浙教版初中數(shù)學幾何例習題有效改編的探究

曹益軍

（浙江省杭州市蕭山區(qū)靖江初中，浙江杭州　311223）

1　研究背景

2014年，蕭山教育局出臺《蕭山區(qū)中小學教師教學規(guī)范（修訂稿）》，其中對教師“教學準備”有如下要求：第2條深度研究教學材料。充分研讀教材，形成自己獨特的理解，同時學習參考其他教學資料，正確理解教學內(nèi)容，把握教學重點和難點。對用于教學的各種練習，要采用“教師自己先做”的方式進行研究，感悟解題的規(guī)律和思路，揣摩學生在解題過程中可能遇到的困難和障礙。

第6條精心準備各類作業(yè)。根據(jù)教學目標與學生實際精心選用和編創(chuàng)作業(yè)。作業(yè)難度合理，數(shù)量適當。關注學生的個體差異，增強作業(yè)的層次性和可選擇性，滿足不同學生的需求。根據(jù)學科特點豐富作業(yè)的形式，增加觀察積累、動手操作、搜集整理、發(fā)現(xiàn)探究、勞動服務等作業(yè)形式。積極探索以引領學生全程學習為目的的導學新作業(yè)模式。

現(xiàn)實教學過程中，教師很多是拿來主義，對已有的教材例題、習題改編的意識不強，在備課中不能對例題、習題進行深層次的挖掘、拓展、再創(chuàng)造，在授課時也往往出現(xiàn)一筆帶過、草草了事的教學現(xiàn)狀，根本沒有很好的利用例題、習題的所潛在的價值，而教材例題、習題的“二次開發(fā)”能促使學生的學習方式由“重結(jié)論輕過程”向“過程與結(jié)果”并重的方向發(fā)展，使學生挖掘隱含問題的本質(zhì)屬性，從而達到“做一題，通一類，會一片”的解題境界，擺脫題海，實現(xiàn)“輕負高效”。

筆者的研究，是結(jié)合本學校的自主教學的實際情況，探討如何更有效地對例題與習題進行合理的選擇、獨特的設計、有效的教學，力求進一步提高我校自編導學案的質(zhì)量，并以此為契機，提高本學科教學質(zhì)量，提升學校辦學品質(zhì)。

2　實踐探微

2.1　改編策略實施

數(shù)學問題改編是對已有數(shù)學問題的條件和結(jié)論部分的內(nèi)容、結(jié)構(gòu)、情境等進行改造，得出新題的一種命題設計方法。改編題較之原本習題不僅承載了知識內(nèi)容，蘊含了數(shù)學思想方法，還被賦予了新的問題情境，傳導了改編者的設計意圖，并以此通過鞏固和變式訓練來實現(xiàn)教學目標。

改編問題的具體方法有：轉(zhuǎn)換條件與結(jié)論、否定條件、題組整合等。

2.1.1　轉(zhuǎn)換條件與結(jié)論

轉(zhuǎn)換條件與結(jié)論，即把原題中的結(jié)論與部分條件互換，使之產(chǎn)生新的問題。如下例：

原題呈現(xiàn)：教科書九上4.5節(jié)《相似三角形的性質(zhì)及其應用》習題 A3（P142）。

已知：如圖1，在△ABC中，AD是角平分線，∠ADE=∠B。

圖1　

求證：AD2=AE·AB

其中， 條件有：（1）AD 是角平分線，（2）∠ADE=∠B，結(jié)論有：AD2=AE·AB。

轉(zhuǎn)換其中的條件和結(jié)論，可得：

改編一，已知：如圖1，在△ABC中，AD是角平分線，AD2=AE·AB。

求證：∠ADE=∠B。

改編二，已知：如圖 1，在△ABC 中，AD2=AE·AB，∠ADE=∠B。

判斷AD是否為△ABC的角平分線，并說明理由。

改編一，是對三角形相似判定的復習，改編二，是不能判定它為角平分線的，這也是學生在相似判定中的一個易錯點。

轉(zhuǎn)換條件與結(jié)論的方法，適合大多數(shù)例題和習題，也是最常用的改編方法。

2.1.2　否定條件法

否定條件法的策略實施，大致可分為四個步驟：

步驟1，選擇習題。

步驟2，列出各個條件。

步驟3，否定各個條件，列出相應的新條件。

步驟4，根據(jù)新條件，提出新問題。

下面結(jié)合一道平行四邊形（三角形的中位線）中的課后作業(yè)題，具體說明否定條件策略在習題改編中的應用。

原題呈現(xiàn)：如圖2，C、D是線段AB上兩點，且AC=BD=AB=1，點P是線段CD上一個動點，在AB同側(cè)分別作等邊△PAE和等邊△PBF，M為線段EF的中點,在點P從點C移動到點D時，點M運動的路徑長度為多少？

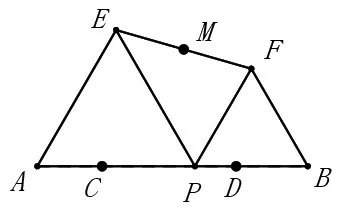
圖2　

第一步，我們首先在步驟1上列出問題中的各個條件：

條件1：C、D是線段AB上兩點；

條件3：在AB同側(cè)；

條件4：等邊△PAE和等邊△PBF；

條件5：M為線段EF的中點；

條件6：點P從點C移動到點D；

條件7：點M運動的路徑長度。

第二步，在步驟2上，我們可依次對所列條件進行否定，并列出新的條件：

條件1否定：“C、D不是線段AB上兩點”，如：點C在線段AB延長線上，情況將如何？

條件 2 否定：“AC≠BD”或“AC=BD≠1”，如:AB=m，AC+BD=n等。

條件3否定：“在AB異側(cè)”，則情況將如何？

條件4否定：“△PAE和△PBF不是等邊三角形”，如:兩個三角形都為等腰三角形，或為正方形，或為其他特殊多邊形。

條件5否定：“M不是EF的中點”，如:M是EF的三等分點。

條件6否定：“點P不是線段CD上一個動點”，如:點P在線段AB上運動。

條件7否定：“不求點M運動的路徑長度”，如:求PM的長度范圍，等等。

第三步，在步驟3上，我們利用一個或若干個新條件提出新問題。

改編一，利用新條件2和4，我們可以得到如下新的問題：

如圖3，線段AB=m，C、D是AB上兩點，且AC+BD=n，點P是線段CD上一個動點，在AB同側(cè)分別作等腰Rt△PAE和等腰Rt△PBF，M為線段EF的中點。在點P從點C移動到點D時，點M運動的路徑長度為多少？

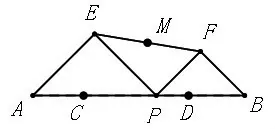
圖3　

改編二，利用新條件6和7，我們可以得到如下新的問題：

如圖4，已知AB=6，點P是線段AB上一個動點，在AB同側(cè)分別作等邊△PAC和等邊△PBD，M為線段CD的中點，連接PM。在點P從點A移動到點B的過程中，求線段PM的最小值。

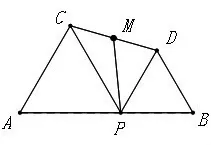
圖4　

改編三，利用新條件4和7，我們可以得到如下新的問題：

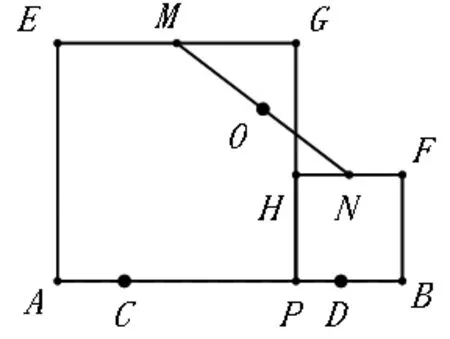
圖5　

通過以上案例，我們可以看到，從一個給定的數(shù)學問題出發(fā)，利用否定條件的策略，以一生十，可以提出豐富多彩的問題。當然，在利用新條件提出問題時，會遇到新條件和其他未被否定的原條件之間不相容的情形，此時提出的問題將是無效的。眾所周知，提出問題比解決問題更重要，我們積極利用否定條件策略，研究問題，這將會編擬出更精彩的數(shù)學問題。教師積極引導學生利用否定條件策略提出問題，這將更能考查一個學生對知識的理解和掌握情況，必將收到事半功倍的效果。

2.1.3　題組整合

重組整合，顧名思義，借助一定的素材，將彼此聯(lián)系緊密的一些例題、習題，串聯(lián)或并聯(lián)起來，可以構(gòu)造出一系列的新問題。如下例：

原題呈現(xiàn)：教科書八上2.1節(jié)《圖形的軸對稱》例2（P50），如圖6，L表示草原上的一條河。一少年從A地出發(fā)，騎著馬去河邊，讓馬飲水，然后回位于B地的家中。他沿怎樣的路線行走，能使路程最短？做出這條最短路線。

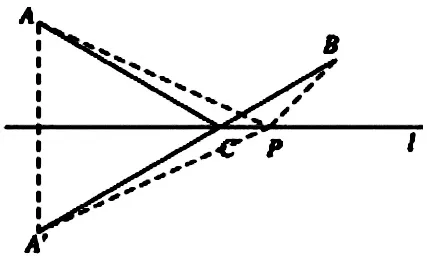
圖6　

本題是利用軸對稱性質(zhì)（PA=PA’）和三角形三邊關系（或兩點間線段最短），解決最值問題。此類問題和解題方法在各種資料中出現(xiàn)頗多，收集并重組整合后，可以得到不少新問題。

改編一，增加一條線（作業(yè)本中練習題）：

如圖7，點P在銳角∠AOB內(nèi)，M、N分別為邊OA、OB上任意一點，連結(jié)PM、PN、MN，當△PMN周長最小時，請在圖上確定M、N的位置。若OP=3，∠AOB=30°，則最小周長為多少。

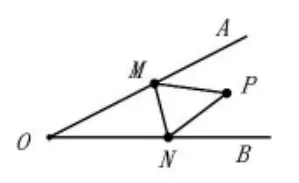
圖7　

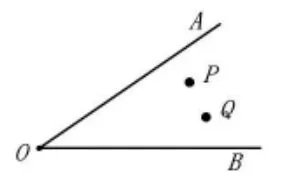
圖8　

圖9　

改編二，增加一個點（導學作業(yè)本習題）：

如圖8，點P、Q在銳角∠AOB內(nèi)，M、N分別為邊OA、OB 上任意一點，連結(jié) PQ、PM、QN、MN，當四邊形PMNQ周長最小時，請在圖上確定M、N的位置。

改編三，把銳角變?yōu)橹苯亲鴺讼担ㄖ锌碱}）：

如圖 9，在直角坐標系中有四個點 A（-3，3），B（-2，5），C、D分別在y軸和x軸上，當四邊形ABCD周長最短時，求C、D的坐標。

改編四，與平移變換結(jié)合（中考題改編）：

如圖10，在直角坐標系中有線段AB=2，CD=1，A（1，2）、B（3,2），C、D 為 x 軸上任意點，當四邊形 ABCD周長最短時，求C的位置。

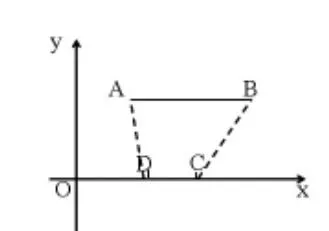
圖10　

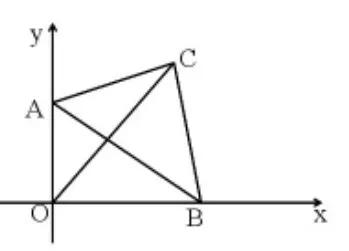
圖11　

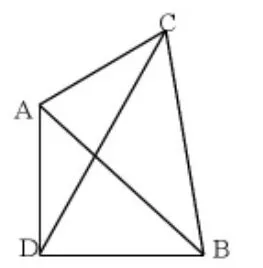
圖12　

改編五，與旋轉(zhuǎn)變換結(jié)合（中考題改編）：

如圖 11，在△ABC 中，AC=3，BC=4，AB=5，頂點 A、B分別y軸和x軸上，當A在y軸上運動時，B隨之在x軸上運動。求運動過程中，點C到點O的最大距離。

改編六，與旋轉(zhuǎn)變換結(jié)合（中考題改編），提升難度：

在改編四基礎上，如圖12，△ABC中，AC=a，BC=b，AB不定，即∠ACB任意，以AB為邊作等腰直角△ABD。當∠ACB變化，且點D與點C位于直線AB的兩側(cè)，求CD的最大值。

此組例題的改編組合，不僅拓展了軸對稱性質(zhì)的應用，而且配以平移、旋轉(zhuǎn)的改編題，讓學生意識到學習圖形變換的真諦：在改變圖形位置、方向后不改變其大小和形狀，圖形變換是分析問題的一種工具。

通過重組整合，改編習題，在強大的網(wǎng)絡資源面前，會非常快捷有效，尤其是在中考復習階段，被大多數(shù)老師所采用，可以快速地形成知識體系。

2.2　經(jīng)典案例分析

原題呈現(xiàn)：教科書九上4.5節(jié)《相似三角形的性質(zhì)及其應用（3）》作業(yè)題 B5（P149），有一塊三角形余料 ABC見圖13，它的邊BC=120mm，高線AD=80mm，要把它加工成正方形零件，使正方形的一邊在BC上，其余兩個頂點分別在AB，AC上。求加工成的正方形零件的邊長。

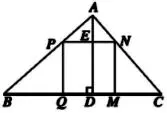
圖13　

本題考查：（1）正方形的性質(zhì)，（2）直角三角形的性質(zhì)，（3）相似三角形的判定和性質(zhì)，（4）方程，（5）基本的幾何分析推理能力。潛在價值：滲透了數(shù)形結(jié)合和建模的思想，應用知識的能力要求較高，能拓展學生的思維空間，提高知識的遷移能力和學生的創(chuàng)新能力。

改編策略一：否定一個條件，如改變其中一個圖形的形狀。

例1：內(nèi)部四邊形改為矩形，如圖14，有一塊三角形余料ABC，它的邊BC=120mm，高線AD長80mm，四邊形PQRS是三角形的內(nèi)接矩形。

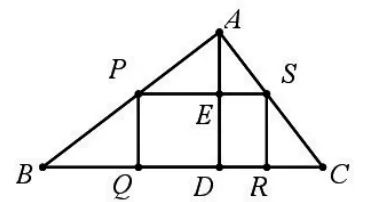
圖14　

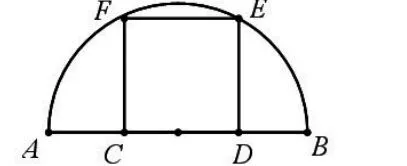
圖15　

（1）當矩形PQRS與△ABC的面積之比為3∶8時，求矩形PQRS的周長；

（2）設PQ長為xmm，求矩形面積S關于x的函數(shù)表達式，并說明點P在何處時矩形的面積最大？

例2：外部三角形改為半圓，如圖15，半圓的直徑AB=10，C、D為直徑上的點，E、F為半圓弧上的點。若四邊形CDEF為正方形，求正方形邊長。

改編策略二：同時否定多個條件，如改變圖形的形狀，或改變圖形的數(shù)量等。

例 3：在△ABC 中，∠C=90°,AC=4,BC=3。

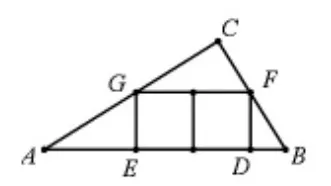
圖16　

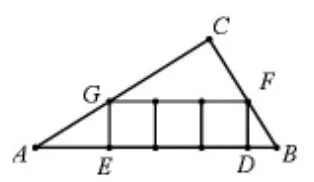
圖17　

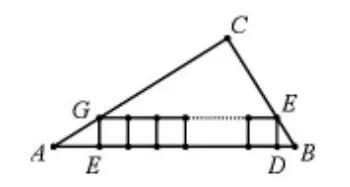
圖18　

（1）如圖16，在△ABC內(nèi)部，并排兩個相同的正方形，它們組成的矩形內(nèi)接于△ABC，求正方形的邊長；（2）如圖17，在△ABC內(nèi)部，并排三個相同的正方形，它們組成的矩形內(nèi)接于△ABC，求正方形的邊長；（3）如圖18，在△ABC內(nèi)部，并排n個相同的正方形，它們組成的矩形內(nèi)接于△ABC，求正方形的邊長。

例 4：如圖 19，在 Rt△ABC 中有邊長分別為 a，b，c的三個正方形，∠C為直角，求a，b，c滿足的關系。（煙臺中考）

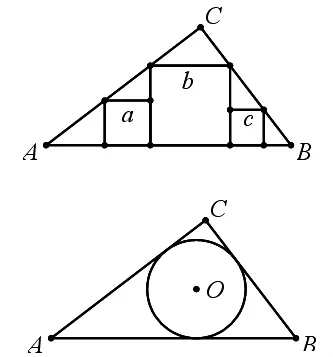
圖19　

例 5：已知 Rt△ABC 中，∠ACB＝90°，AC＝6，BC＝8。

如圖20，若半徑為r的⊙O是Rt△ABC的內(nèi)切圓，求r。

圖20　

例6：一張等腰三角形紙片，底邊長13cm，底邊上的高為32．5cm，現(xiàn)沿底邊依次從下往上裁剪寬度均為5cm的矩形紙條，如圖21所示。已知剪得的紙條中有一張是正方形，則這張正方形紙條是第幾張？（溫州中考）

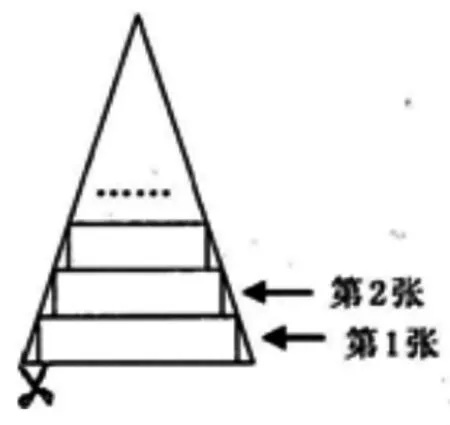
圖21　

改編策略三：整合多個例題。

例 7：整合例 1和例 5，如圖 22，四邊形 PQRS為Rt△ABC 的內(nèi)接矩形，∠ACB＝90°，三個內(nèi)切圓的半徑從小到大依次為r1,r2和r3。當內(nèi)接矩形的面積達到最大時，求r1,r2,r3滿足的數(shù)量關系。

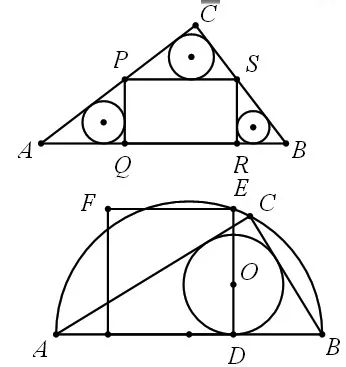
圖22　

例8：整合例2和例5，如圖23，AB為半圓的直徑，C是半圓弧上一點，正方形DEFG的一邊DG在直徑AB上，另一邊DE過ΔABC的內(nèi)切圓圓心O，且點E在半圓弧上。（1）若正方形的頂點F也在半圓弧上，則半圓的半徑與正方形邊長的比是______；（2）若正方形DEFG的面積為100，且ΔABC的內(nèi)切圓半徑r=4，則半圓的直徑AB=______。（杭州中考）

圖23　

一道練習通過否定條件、題組整合等多種形式的改編，運用在課堂教學中，促使學生對初中數(shù)學知識的融會貫通，創(chuàng)建學生自主建模的能力，培養(yǎng)學生掌握數(shù)學思想與方法，培養(yǎng)學生思維的靈活性、深刻性和創(chuàng)造性，提高學生的數(shù)學素質(zhì)，增強學生解題技巧。

3成效與反思

自從開展本課題研究以來，我們都積極嘗試著自己編出幾道題，很高興、很管用。至今，已編出一套非常適用本校教學的習題集，所編的題在多種重大考試中使用，命題質(zhì)量受到同行好評。

那么，怎樣才能改編出好題呢？筆者認為還需要做到以下三點：（1）加強對題目的記憶，好題可以收集，它是編題的素材；（2）多解題，多思考，提高敏銳性，關注各種題目之間的聯(lián)系；（3）關注學生的錯誤，難題、易錯題改編價值更高。

通過例習題改編，對現(xiàn)行教材進行大膽處理，真正開辟了一條輕負高效的好路子。我校是自主學習的特色學校，近年來積極參與新課程改革，推行先學后教的教學新范式，本課題的研究，也符合數(shù)學學科在課程改革中的要求，堅持了一年多的團隊實踐，不僅改變了我們課題組老師的教學方式，而且還收集整理了一份以教材改編為主的學案集，極大地提高了我們的教學質(zhì)量。我們?nèi)谓痰哪昙墸诟骷壐黝惐荣惪荚囍校黜椫笜硕歼h超片常模。

數(shù)學新課程改革是一個在探索中發(fā)展的過程，需要所有數(shù)學教育工作者的共同努力。今后，在課堂新范式的推進、數(shù)學教材的處理、數(shù)學試題的改編過程中，我們將繼續(xù)和其他同行一起，深入研究教學問題，擴大實驗成果。本課題的研究與實施，已經(jīng)變革了我們課題組老師的的教學方式，并且我們也從中獲益不少，值得我們繼續(xù)為之努力。

[1]李志敏.如何設計新題[J]．數(shù)學通報，2010(8)：37-40.

[2]潘超．變有限意無窮——談基于“幾何畫板”的變式探究[J]．中學數(shù)學教學參考:初中版，2012(11)：47－49.

[3]沈雪明．用課本例題解競賽題例說[J]．中等數(shù)學，2005(10)：13-14.

[4]黎奇.新課程背景下的有效課堂教學策略[M].北京：首都師范大學出版社，2010.