基于Bagging集成聚類的改進遺傳算法在裝配線平衡中的應用*

□ 李愛平 □ 趙亞西

同濟大學機械與能源工程學院 上海 201804

1　研究背景

在企業實際生產中，改善裝配線的生產效益是研究重點。裝配是制造與信息控制相結合的過程，設計出優良的裝配線平衡方案，能夠使裝配線高效且可靠地運行，進而提高生產效率，增加企業效益，可見，研究裝配線平衡具有很大的實際意義。裝配線平衡問題按不同的優化目標主要分為三類［1-2］：① 生產節拍一定，求最優工作站數；② 工作站數固定，求最優生產節拍；③工作站數已知，求最優平滑因子。裝配線平衡問題是典型的非確定多項式難題，對于求解算法有較高的要求，近年來主要以遺傳算法等啟發式算法為主，由于算法可行解過多，為了搜索出更優的可行解，算法需要改進。

張子凱等［3］針對大規模混流U型裝配線平衡問題，提出了一種基于多級隨機分配編碼的改進遺傳算法，算法在降低計算復雜度的同時能準確求出問題較優解。梁雨生等［4］針對裝配線平衡問題，提出了一種基于可行作業序列的多種群遺傳算法，擴大了搜索的空間范圍，有效避免產生局部最優的情況。扈靜等［5］針對傳統混合裝配生產線缺乏一工位多產品研究的現狀，設計了基于激素調節機制的改進遺傳算法適應度函數，以及選擇、交叉與變異算子，對一工位多產品的混合裝配生產線平衡問題模型進行求解，提升了算法性能。董雙飛［6］結合遺傳算法與混流裝配線的特點，對遺傳算法中初始種群的產生、算法的可視化操作、交叉與變異操作的方式及概率的設置進行改進，并提出種群擴張機制，提高了算法的全局搜索能力。李險峰［7］針對傳統遺傳算法在種群數目有限的情況下呈現早熟問題進行分析，提出并實現了一種加入改進遺傳算子策略，且結合模擬退火思路的混合遺傳算法。韓煜東、董雙飛等［8］設計了基于自然數序列和拓撲排序的改進遺傳算法，對模型進行求解時通過改進交叉、變異操作來保護優秀基因，同時提出了種群擴張機制，在求解效率和求解質量方面取得顯著成效。劉雪梅等［9］基于工位復雜性測度提出了一種隨機型裝配線平衡優化方法，并將基于動態步長法的改進遺傳算法用于優化求解。陳星宇［10］提出一種雙種群遺傳算法，設計了基于優先關聯矩陣的編碼、譯碼，以及適應度設計、交叉選擇和變異算子，在求解裝配線平衡問題時有顯著成效。Hou Liang等［11］針對產品族裝配線提出了一種改進的雙種群遺傳算法，同時為了彌補傳統解碼方法的不足，提出了一種新的解碼算法，加快了算法的搜索速度。

綜上所述，學者們從編碼、解碼、交叉、變異、選擇等各環節對遺傳算法做出改進，但是尚未從近親不能繁衍后代的生物學角度考慮算法的改進方式。筆者為了提高遺傳算法的搜索深度，考慮生物學角度近親不能交叉的規則，建立一種Bagging集成聚類方法用于分析種群個體間的親緣關系，并基于此方法改進遺傳算法的交叉環節，在雙目標裝配線平衡優化問題中提高算法的搜索深度，得到更優的可行解。

2　基于Bagging集成聚類的種群聚類分析

傳統遺傳算法在求解裝配線平衡等非確定多項式難題時，常常表現出搜索深度不足的問題，為了提高遺傳算法的搜索深度，筆者提出一種Bagging集成聚類算法，用Bagging對幾個K均值算法基學習器進行集成學習，經過投票機制后得出每個種群個體所屬的類別。

2.1　K均值聚類算法

K均值算法的原理是使聚類的所有樣本到聚類中心距離的平方和最小，是經典的硬聚類算法。

K均值聚類算法使用的聚類準則函數是誤差平方和準則：

為了優化聚類結果，應使準則最小化。

第一步，給出n個混合樣本，令I=1，表示迭代次數，選取 K 個初始聚合中心 Zj（I），j=1，2，...，K。

第二步，計算每個樣本與聚合中心的距離D（xk，Zj（I）），k=1，2，...，n，j=1，2，...，K。 若 D（xk，Zj（I））=min｛D（xk，Zj（I）），k=1，2，...，n｝，則 xk∈wi。

第三步，計算 K 個新聚合中心，Zj（I+1）=，j=1，2，...，K。

第四步，判斷若 Zj（I+1）≠Zj（I），j=1，2，...，K，則將I+1賦值給I，返回第二步；否則，算法結束。

筆者的K均值聚類算法采取成批處理法進行初始分類的選取和調整，代表點就是聚類中心，選一批代表點后，計算其它樣本到聚類中心的距離，將所有樣本歸于最近的中心點，形成初始分類，再重新計算聚類中心。

2．2　K均值集成聚類

2.2.1集成學習

集成學習是利用幾個學習器進行綜合學習。先選定幾個個體學習器，然后使用一些結合方法進行結合。很多經典的機器學習算法，如隨機森林法等都是采用集成學習建立的。隨機森林法由多個決策樹算法集成，這種個體學習器稱為基學習器。集成學習結構圖如圖1所示。

▲圖1 集成學習結構圖

2.2.2 Bootstrap

想要得到泛化性能強的集成，集成中的個體學習器應當盡可能相互獨立。雖然獨立在現實任務中無法做到，但可以設法使基學習器盡可能具有較大的差異。Bootstrap是統計學習中的一種重采樣技術，這種看似簡單的方法，對之后的很多技術都產生了深遠影響。機器學習中的Bagging、AdaBoost等方法其實都蘊含了Bootstrap的思想。

在統計時，面臨的只有樣本，樣本具有明顯的不確定性。正因為不確定性的存在，才使統計能夠生生不息，統計的意義也就在于基于樣本推斷總體。Bootstrap方法最初由美國斯坦福大學統計學教授Efron在1977年提出，作為一種嶄新的增廣樣本統計方法，Bootstrap方法為集成學習的采樣提供了很好的思路。

2.2.3 Bagging

Bagging是并行式集成學習方法中最著名的代表。給定樣本容量為n的數據集，先隨機取出一個樣本放入采樣集中，再將樣本放回初始數據集，使下次采樣時該樣本仍有可能被選中，這樣經過v次隨機抽樣，得到含v個樣本的采樣集。初始訓練集中有的樣本在采樣集中多次出現，有的則從未出現。重復抽樣過程T次，則得到T個樣本容量為v的Bootstrap樣本，記為Di=（x1，x2，...，xv），i=1，2，...，T。

采樣出T個含v個訓練樣本的采樣集，然后基于每個采樣集訓練出一個基學習器，再對這些基學習器進行結合，這就是Bagging的基本流程。在對結果進行輸出結合時，Bagging通常使用投票原則。

2.2.4 K均值集成聚類算法

K均值聚類算法在機器學習中屬于無監督學習，即使用沒有標簽的數據進行學習。集成學習使用多個基學習器來降低模型泛化誤差中的偏差和方差。將以上兩個概念結合起來，就是無監督集成學習，即對沒有標簽的數據使用集成算法。

將K均值與Bagging結合，生成K均值集成聚類算法，算法具體流程如圖2所示。

▲圖2 K均值集成聚類算法流程

第一步，按Bootstrap方式，對初始訓練集進行v次有放回的隨機抽樣，重復T-1次抽樣過程，采樣出T-1個含v個訓練樣本的Bootstrap采樣集，記為Di=（x1，x2，...，xv），i=1，2，...，T-1。

第二步，由于存在未被抽樣的樣本，因此當每個樣本都需要歸類時，需要將剩余所有未被抽樣的w個樣本取出，組成最后一個采樣集，記為 DT=（x1，x2，...，xw），則總的采樣集記為：

第三步，將T個采樣集分別用K均值基學習器來單獨進行聚類訓練，設初始訓練集樣本數為z，聚類類別數為K，建立一個z·K維矩陣，用于記錄每個個體學習器對每個樣本聚類類別的投票情況，第i行第j列的數字s表示有s個基學習器將第i個樣本歸類為第j類。

第四步，根據建立的z·K維矩陣，按照投票法則來決定每一個樣本的最終聚類類別。樣本的最終類別由票數最多的類別決定，若存在投票數相同的類別，則在其中隨機選擇一個類別作為該樣本最后的聚類類別。

3　雙目標裝配線平衡優化數學模型

筆者在工作站數固定和作業元素優先關系的約束條件下，將裝配線生產節拍和平滑因子作為優化目標，建立雙目標裝配線平衡優化模型。

3.1　約束條件

C為生產節拍，I為作業元素集合，J為工作站集合，n為作業元素個數，mi為種群中第i個個體的實際工作站數目，M為確定的工作站數，Jk為第k個工作站的作業元素集合， k∈（1，M）。

x為一維向量，表征各裝配作業元素排序情況，若x=［x1，x2，...，xn］， 滿足所有約束條件的 xi即為可行解。X為n·M維矩陣，表征各裝配作業元素在工作站上的分配情況，對于 X（i，k）∈X，若 X（i，k）=1，則表示裝配作業元素 i分配在工作站 k；若 X（i，k）=0，則表示裝配作業元素i未分配在工作站k。PPred為n×2維優先關系集合，PPred（i，1）是 PPred（i，2）的前序作業元素。 P 為 n·n維優先關系矩陣，對于 P（k，i）∈P，若 P（k，i）=1，則表示 k 為 i的前序作業元素；若 P（k，i）=0，則表示 k 為 i的后序作業元素。ti為第i道作業元素的作業時間。

在企業實際生產中，裝配線常常已經建立完畢，若改建或擴建，則成本高昂，所以工作站數是一定的。

每個作業元素只能分配到一個工作站上，即：

要在滿足優先關系的條件下分配作業元素，即：

各工作站的作業總時間小于等于生產節拍，即：

工作站數是一定的，即：

3.2　優化目標

筆者選擇優化目標為生產節拍C和平滑因子SI，因為減小生產節拍C能起到縮短總空閑時間的作用，而平滑因子SI是評價裝配線負荷平衡的指標，負荷平衡的作用是提高人員和設備利用率。優化目標定義為min C ，min SI。

其中，生產節拍C的定義是工作站作業時間的最大值，T（k）為第k個工作站的作業時間，則有：

平滑因子SI為：

3.3　數學模型

綜合約束條件和優化目標，定義如下數學模型：

4　基于Bagging集成聚類的改進遺傳算法

為提高遺傳算法的搜索深度，筆者基于Bagging集成聚類算法的種群聚類分析方法，對遺傳算法的交叉部分進行改進，判斷隨機配對的兩個體是否是屬于同一族群的近親，避免近親個體交叉。

4.1　算法流程

記Spop為種群數目，要求是2的倍數，Ppop（t）為第t代種群，G為遺傳代數，Pc為交叉概率，Pm為變異概率，其余參數定義同前，則改進遺傳算法流程如下。

第一步，初始值設定。 輸入 Spop、G、C、M、Pc、Pm、T、v、K 的值。

第二步，初始化種群。令t=0，隨機產生滿足約束、數量為 Spop的初始種群 Ppop（0）。

第三步，適應度計算。對第t代種群Ppop（t）中每個個體計算適應度參考值，即染色體的生產節拍C和平滑因子SI。

第四步，懲罰策略。檢查種群中的個體是否滿足約束條件，若不滿足工作站數固定為M的約束，則給此個體適應度一個懲罰項，將兩個適應度參考值變為某極大值，如500。

第五步，雙目標并列選擇操作。根據兩個適應度參考值，分別選出兩個適應度參考值最優的s個個體，s=Spop/2，然后重組為新種群，作為第t+1代種群。

第六步，交叉操作。利用Bagging集成聚類算法對交叉規則進行改進，交叉形式采用單點交叉。

第七步，變異操作。變異規則采用單點變異。

第八步，循環。將t+1賦值給t，如果滿足停止條件，結束；否則轉向第三步。

4.2　編碼與策略

在滿足作業元素優先關系的約束條件下，對所有作業元素進行排列。每個作業元素對應染色體的一個基因位，排列好的個體記為一條編碼染色體。

在交叉變異后，對種群中的個體重新做約束檢查。若某個體不滿足工作站數固定的條件，則對該個體的兩個適應度參考值生產節拍C和平滑因子SI給予一個懲罰項，如500。由于懲罰項較大，因此被懲罰的個體容易在選擇環節淘汰。

對第t代種群Ppop（t），根據計算好的每個個體適應度參考值生產節拍C和平滑因子SI，獨立選出最優的前1/2個體，然后組成新的第t+1代種群。

4.3　交叉操作

遺傳算法中，個體以編碼形式存在，可以將各編碼值看作個體的特征值，用聚類方法來判斷兩個體是否屬于近親。K均值屬于硬聚類，是一種弱學習器，學習效果有限。將多個K均值進行結合，則得到超越個體學習器的優越泛化性能。筆者通過之前建立的基于Bagging的K均值集成聚類方法改進遺傳算法的交叉操作。

由交叉概率 Pm決定第t代種群 Ppop（t）發生交叉的概率，交叉具體規則為單點交叉，具體如下。

第一步，將排序打亂，隨機配對。

第二步，對第t代種群Ppop（t）中所有個體，采樣出T個含v個訓練樣本的采樣集。將剩余所有未被抽樣的w個樣本作為最后一個采樣集，對采樣集進行Bagging K均值集成聚類算法，聚類類別數為K，根據投票法則得到每個個體的聚類類別。

第三步，對比隨機配對的兩個體所屬的聚類類別，若兩者屬于同一類別，則當前兩個體不交叉，跳過，進行下一組；否則，兩個體進行交叉，交叉采用單點交叉規則。

5　實例分析

為了驗證筆者算法的深度搜索能力，以某汽車變速箱裝配線為實例，對該條裝配線進行平衡優化。汽車變速箱裝配體由三個主要部分組成，作業元素數量n=27，優先關系如圖3所示。裝配線的工作站已建立好，工作站數M=12，若改建或擴建，則成本高昂。

對該裝配線進行平衡優化，在工作站數固定為M=12的約束下，以生產節拍C和平滑因子SI為優化目標，利用提出的改進型遺傳算法進行求解，提高搜索深度。

5.1　雙目標優化求解

利用MATLAB 2015b編程求解，數學模型的參數設定如下：固定工作站數M=12，交叉概率Pc=0.6，變異概率Pm=0.05，遺傳代數 G=50，種群數量 S=200，生產節拍初始值C=130 s。

當設定T=5、v=60、K=3時，生產節拍C和平滑因子SI的優化過程分別如圖4和圖5所示。優化過程記錄了每代種群中C和SI的最優值。

由圖4和圖5可知，兩個目標都得到了優化。生產節拍優化比較容易，在5代以內得到最終優化值。平滑因子在不斷優化，在40代后收斂，沒有過早收斂。選取一些具有代表性的優秀解，見表1、表2。

▲圖3 汽車變速箱裝配優先關系

由表1、表2可見，生產節拍C和平滑因子SI兩個目標均得到了優化，提高了裝配效率，減少了總空閑時間，算法對可行解進行了深度搜索，優化出多個較優解。

▲圖4 生產節拍優化過程

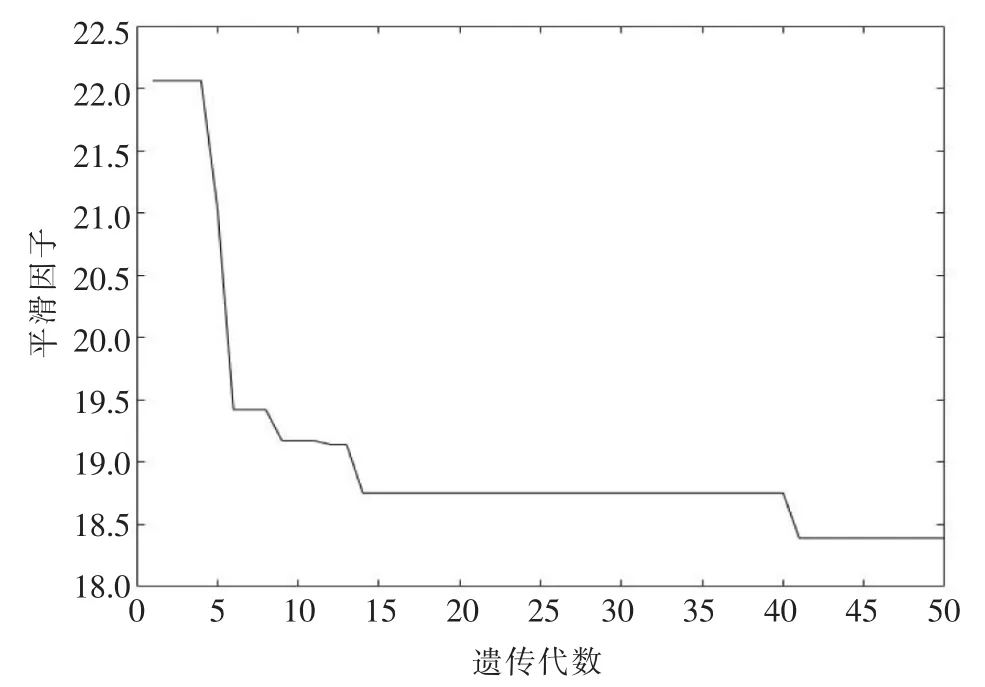
▲圖5 平滑因子優化過程

表1　作業元素分配方案1

5.2　方案對比

基于Bagging集成聚類的改進遺傳算法在不同主要參數設置時，搜索深度會有差異，主要參數包括T、v和K。為證明改進后的遺傳算法搜索深度確實有提升，對參數進行不同設置，做對比試驗。一是給定不同的T、v、K進行優化，二是利用未改進的遺傳算法進行求解。進行多組對比試驗，取兩個目標數值之和最小的解為代表，對比結果見表3。

表2　作業元素分配方案2

表3　方案對比

由表3分析可知，每組試驗得到的平衡方案中生產節拍C優化解都相同，而平滑因子SI則不相同，這說明從單一的優化目標角度來看，生產節拍的優化較為容易，平滑因子的優化則較難，不同參數設置下得到的搜索深度不同。對比各組試驗結果，用改進遺傳算法求出的優化解在不同參數設置下的結果并不相同，搜索深度有差別；整體上，用改進遺傳算法求出的優化解明顯優于未改進遺傳算法。綜上所述，基于Bagging集成聚類的改進遺傳算法，相比未改進的遺傳算法，搜索深度更深，能得到更優的解。

6　結束語

筆者從生物學中近親不能交叉的角度考慮，建立了一種基于Bagging集成聚類算法的種群聚類分析方法，利用這一方法判斷種群中的兩個體是否屬于近親，進而改進了遺傳算法的交叉規則。以生產節拍和平滑因子為優化目標，建立了雙目標裝配線平衡模型，將改進遺傳算法應用于雙目標裝配線平衡實例中。實例顯示，改進遺傳算法相比未改進遺傳算法，有效提升了算法的深度尋優能力。

［1］ 竇建平，蘇春，李俊.求解第Ⅰ類裝配線平衡問題的離散粒子群優化算法［J］.計算機集成制造系統， 2012， 18（5）：1021-1030.

［2］ 鄭巧仙，李元香，李明，等.面向第Ⅱ類裝配線平衡問題的蟻群算法［J］.計算機集成制造系統， 2012， 18（5）：999-1005.

［3］ 張子凱，唐秋華，張利平，等.改進遺傳算法求解大規模混流 U型裝配線問題 ［J］.機械設計與制造，2016（1）：137-139.

［4］ 梁雨生，李向波.基于遺傳算法的裝配線平衡問題研究［J］.價值工程， 2013， 32（5）：123-125.

［5］ 扈靜，蔣增強，葛茂根，等.基于改進遺傳算法的混合裝配生產線平衡問題研究［J］.合肥工業大學學報（自然科學版），2010， 33（7）：1006-1009.

［6］ 董雙飛.基于改進遺傳算法的混流裝配線多目標平衡優化研究［D］.重慶：重慶交通大學，2015.

［7］ 李險峰.基于改進遺傳算法的汽車裝配生產線平衡問題研究［D］.北京：北京科技大學，2017.

［8］ 韓煜東，董雙飛，譚柏川.基于改進遺傳算法的混裝線多目標優化［J］.計算機集成制造系統， 2015， 21（6）：1476-1485.

［9］ 劉雪梅，蘭琳琳，顧佳巍，等.基于工位復雜性測度的隨機型裝配線平衡優化方法 ［J/OL］.計算機集成制造系統，http：//kns.cnki.net/KCMS/detail/11.3619.TP.20170627.1615.006.html.

［10］陳星宇.基于改進遺傳算法的裝配生產線平衡技術研究［D］.上海：上海交通大學，2011.

［11］ HOU L，WU Y M，LAI R S，et al.Product Family Assembly Line Balancing Based on an Improved Genetic Algorithm［J］.The International Journal of Advanced Manufacturing Technology， 2014，70（9-12）：1775-1786.