大型風力發電機組塔頂法蘭應力集中因數的有限元分析

□趙云琨 □李佳威 □劉恒山 □許夢華 □潘文豪

上海電氣風電集團有限公司 上海 200030

1 研究背景

隨著風力發電行業各項相關技術的快速發展，風力發電機組的功率越來越大。在兆瓦級大型風力發電機組中，塔架是重要的承載部件。塔架除了要支撐風力發電機組的重力，還要承受吹向風力發電機組和塔架的風壓，以及風力發電機組運行中的動載荷，其設計水平將直接影響風力發電機組的性能[1]。塔頂法蘭是連接塔架和前機架的關鍵部件，也是風力發電機組運行時塔架的主要受力部件，與偏航剎車盤、偏航軸承通過螺栓連接。在風力發電機組工作時，作用于葉輪和機艙的載荷通過偏航軸承傳遞到塔架上，因此塔頂法蘭連接的可靠性和安全性對整個風力發電機組的正常運行而言有重要影響。

法蘭連接系統所承受的是復雜多變的動載荷，在這些載荷作用下，系統各個部件可能發生屈服或疲勞損壞[2]。風力發電機組運行過程中，風輪旋轉帶來升力、阻力、軸向推力、氣動彎矩和氣動轉矩等氣動載荷，加之輪轂的不間斷無規律震蕩、微旋轉等運動載荷，通過偏航軸承傳遞到塔架法蘭和螺栓上[3]。塔筒間焊縫處和法蘭圓角過渡處是結構中比較薄弱的環節，塔頂法蘭由于長期承受動態載荷，易發生疲勞損壞。如果能在設計初期對焊縫和圓角的疲勞壽命進行預測，就可以對焊縫處理方式和圓角尺寸進行合理調整，進而提高產品的整體抗疲勞性能[4-5]。為了測算焊縫處和法蘭圓角過渡處應力集中對法蘭疲勞損壞的影響，在疲勞計算時引入應力集中因數用以放大時序載荷。根據應力集中對疲勞損壞的影響，針對焊縫處和圓角處進行必要的修整，以降低應力集中因數，進而減小法蘭疲勞損壞。可見，為提高塔頂法蘭使用壽命，進而提升風力發電機組運行的可靠性，對塔頂法蘭應力集中因數進行計算是非常必要的。

應力集中往往受法蘭受力狀態影響，為具體分析法蘭應力集中現象，首先進行法蘭連接狀態的受力和變形分析。筆者采用有限元仿真技術，結合相關理論對塔筒頂部法蘭應力集中因數進行分析。有限元仿真采取整體建模和子模型共同分析的方法，分別計算塔頂法蘭焊縫及過渡圓角等危險處的應力集中因數，在實際應用中利用該因數對塔頂法蘭疲勞強度加以校核，同時采取減小應力集中因數的方法進行法蘭加固。

2 法蘭受力理論分析

風力發電機組通過法蘭實現兩塔筒節間，以及塔頂塔筒與偏航軸承、前機架等之間的連接。塔架在彎矩作用下發生振動，常見的振動方式為筒體左右擺動。

筒體擺動使連接法蘭發生交替拉壓變形，不但使法蘭產生應力集中現象，而且造成法蘭間交替出現縫隙或擠壓變形。變形產生的法蘭間隙不僅對螺栓的疲勞壽命造成不利影響，而且會增大法蘭的疲勞損壞，嚴重影響法蘭連接系統的結構強度[6]。

為了直觀地進行塔頂連接法蘭受力和變形分析，將偏航軸承和前機架等簡化為一塊整體法蘭，與塔頂法蘭經高強度螺栓連接形成法蘭連接系統，其受力和變形理論同兩塔筒節間理論相同。根據機械受力原理，分析法蘭在彎矩作用下發生的變形。不考慮法蘭連接后自存間隙及螺母端面與法蘭間摩擦，結合圖1和圖2分析法蘭受力及變形[7]。

風機處于不工作狀態時，法蘭僅受預緊力作用，發生如圖2（a）所示擠壓變形。預緊力指向螺栓外部，兩法蘭受擠壓產生反作用力F0，單一法蘭在連接部位分別受預緊力FF和F0，此時殘余預緊力FCF=F0，連接部分因擠壓而在兩側產生間隙。

加載彎矩后，整體法蘭發生傾覆變形，體現在法蘭連接處為拉伸或壓縮變形。如圖2（b）所示，在彎矩作用下，螺栓承受向上工作拉力F，總拉力為FCF+F。法蘭承受的壓縮力為殘余應力F1，且持續壓縮，同時，法蘭經受向內傾覆的彎矩，因此外側間隙加大，內測間隙減小。最終法蘭和螺栓受力達到平衡，法蘭總力F1=FCF+F。如圖2（c）所示，螺栓在壓力Fm作用下產生壓縮，而法蘭在F1m作用下釋放原始間隙，同時在傾覆力矩作用下法蘭內側產生間隙。最終螺栓與法蘭受力平衡，法蘭總力F2m=F1m-Fm。對比法蘭拉壓兩側總力可見，F1＞F2m，即受拉側法蘭受力大于受壓側，受拉側更易發生應力集中。

圖1 法蘭螺栓受力變形示意圖

風力發電機組運行過程中，法蘭因承受動載荷發生斷續拉壓變形，法蘭拉壓兩側受力狀態不同，其應力分布亦不同，即應力集中會發生變化，因而損壞部位及程度也會不同。由于法蘭應力集中易發生在圓角過渡處及與筒壁焊接的焊縫處，因此需要建立包含過渡圓角和焊縫的子模型，并加載總體模型位移在子模型上，分析子模型在不同拉壓狀態下圓角過渡處及與筒壁焊接焊縫處的應力分布，同時獲得應力集中因數。

3 有限元結構分析

3.1 法蘭有限元建模

仿真計算過程分為整體模型仿真計算和子模型仿真計算。塔頂整體有限元模型包括前機架假體、偏航軸承、剎車盤、塔頂法蘭、部分塔筒及相應的連接螺栓等，如圖3（a）所示。不同的部件材料，其特性不同，建模時需考慮的參數也不相同，表1給出了不同部件的材料參數，各接觸面間摩擦因數取0.15[8]。子模型以較小的區域包含法蘭的圓角和焊縫，在圓角處采用六面體加密網格，焊縫采用一圈節點模擬，與節點相關的單元采用較小網格，如圖3（b）所示。應用子模型可以在研究塔頂法蘭應力集中時獲得足夠精確的應力分布。

3.2 邊界條件和加載

根據實際裝配和受力情況，對模型邊界進行約束。將塔架下端通過質量點單元統一約束6個自由度，以消除接觸分析時的剛體位移[9]。為了反映真實受力狀態，在塔頂法蘭偏航剎車盤中心點處加載極限組合彎矩，并將極限載荷分10個子步逐一加載至模型。考慮到存在法蘭連接螺栓預緊力，將加載載荷的第一子步設置為加載預緊力，從第二子步開始加載極限載荷分量。根據極限工況設置最大組合彎矩為8 764.520 kN·m。整體模型中螺栓均布于塔頂法蘭，單一螺栓預緊力F0為510.00 kN，預緊因數γo為1.2，預緊力損失F1為9.00 kN。

表1 材料物理力學性能

圖2 法蘭受力變形示意圖

圖3 塔頂有限元模型

根據公式F=F0/γo-F1[10]，計算單一螺栓實際預緊力F為416 kN。塔頂共有72個螺栓，這樣單個預緊單元上加載的力為29 952 kN。

3.3 整體模型有限元分析

在軸心處加載垂直于YOZ平面的順時針彎矩，得出塔頂整體模型位移圖和塔頂法蘭位移圖，分別如圖4、圖5所示。由圖4可知，塔頂沿著彎矩方向受到壓應力而發生擠壓，反方向則發生拉伸，最大位移為0.002 907 m。塔頂法蘭與偏航剎車盤、偏航軸承等連接等效于與法蘭連接，單獨分析法蘭應力狀態，由圖5可知，法蘭最大位移出現在塔筒兩側，最大變形量為0.001 091 m。法蘭變形小于塔頂最大變形量，主要是由于法蘭和塔頂之間有前機架體緩沖頂部力的作用。

圖4 塔頂整體模型位移圖

圖5 塔頂法蘭位移圖

由于變形由應力集中引起，因此結合位移分析塔頂法蘭受力情況。圖6為塔頂應力分布情況，塔頂在彎矩作用下最大應力為900 MPa，發生在塔筒軸向左側，右側應力集中最大值約為400 MPa，與軸向兩側成90°位置幾乎不受力。在應力作用下，法蘭發生拉伸和壓縮，為進一步確定法蘭狀態，進行法蘭第一主應力分析。由圖7可知，塔頂右側受壓應力，最大為-55.1 MPa；左側受拉應力，最大為173 MPa。由此可見，塔頂受拉側應力集中大于受壓側，受拉側變形大于受壓側，即受拉側較危險。

圖6 塔頂整體模型應力圖

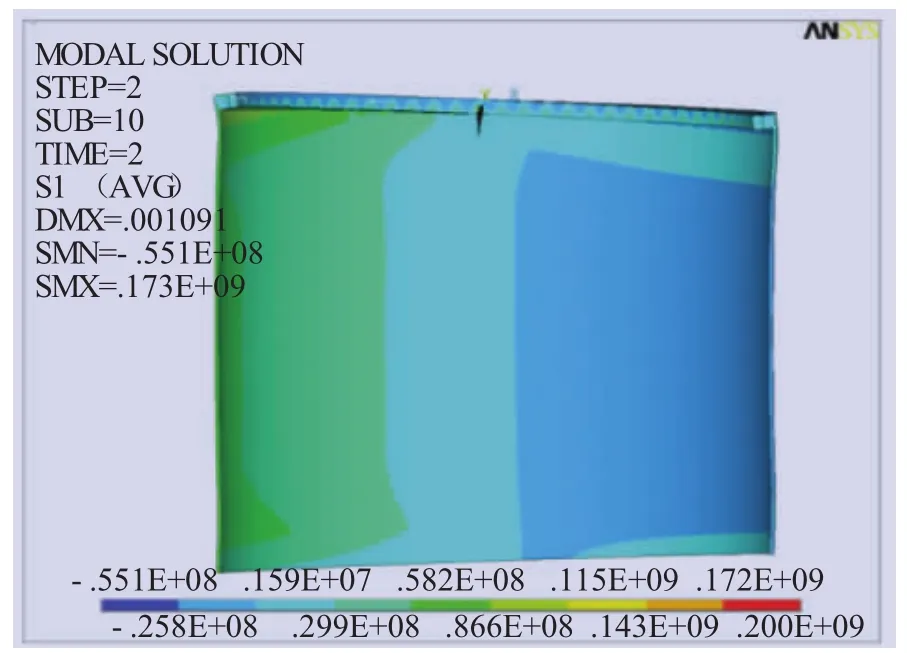
圖7 塔頂法蘭第一主應力圖

3.4 子模型有限元分析

3.4.1 法蘭受壓有限元分析

在完全彎矩作用下，塔頂出現最大應力和變形，對塔頂危險區域圓角過渡處和焊縫處建立子模型進行進一步分析。如圖8所示，受壓測法蘭圓角過渡處產生最大應力為118 MPa，筒壁上應力逐漸減小。對焊縫處進行第三主應力分析，如圖9所示，法蘭焊縫處產生最大壓應力為-96 MPa，焊縫兩側壓應力均逐漸減小，甚至在法蘭連接面出現拉應力。由于焊縫僅是一圈節點，無法顯示，圖中代表節點的線即為焊縫。圓角最大應力大于焊縫最大應力，焊縫處相較圓角處更安全。

3.4.2 法蘭受壓應力集中因數計算

為確定塔頂法蘭疲勞強度，需采用有限元方法分析塔頂法蘭的應力集中因數。應力集中因數與名義應力σNominal相關，將σNominal分10個子步加載至法蘭上，得到法蘭危險應力后，計算應力集中因數。實際應用中，根據應力集中因數隨法蘭厚度、高度等參數的變化進行結構優化，以期在結構合理的基礎上獲得最小的應力集中因數。

圖8 法蘭受壓應力圖

圖9 法蘭受壓焊縫第三主應力圖

應力集中因數主要針對危險位置進行計算。法蘭易在圓角過渡處和焊縫處產生應力集中，因此主要分析法蘭圓角和焊縫處的應力集中因數。應力集中因數K的計算基于名義應力和極限載荷作用下的法蘭應力，有：

式中：σmax（t）為第t子步最大應力；σmax（0）為初始最大應力。

根據加載的極限彎矩，σNominal為63.04 MPa。

分別計算每個加載子步下的應力集中因數，得受壓側焊縫和法蘭圓角處應力集中因數曲線，分別如圖10、圖11所示。

對受壓側應力集中因數進行研究，發現無論是圓角處還是焊縫處的應力集中因數，均隨加載載荷的增大而逐漸減小，并最終趨于穩定。這是由于受壓側的法蘭變形、隨應力增大而趨于穩定，焊縫和圓角處應力亦逐漸趨于穩定。圓角處應力集中因數相比焊縫處較大，實際應用中需加大過渡圓角半徑，同時加厚法蘭壁，以達到增強法蘭強度的效果。

圖10 受壓側焊縫應力集中因數曲線

圖11 受壓側法蘭圓角處應力集中因數曲線

3.4.3 法蘭受拉有限元分析

在完全彎矩作用下，圖12和圖13分別顯示了法蘭受拉應力和焊縫第一主應力，其中圓角過渡處為危險區域。法蘭圓角過渡處產生最大應力為129 MPa，筒壁上應力逐漸減小，且法蘭連接面應力迅速減小。法蘭焊縫處產生的最大拉應力為103 MPa，焊縫兩側壓應力均逐漸減小。由于筒壁連接處較薄，受力集中較嚴重，筒壁連接處應力減小速度小于法蘭連接面。

圖12 法蘭受拉應力圖

3.4.4 法蘭受拉應力集中因數計算

根據有限元計算原理，采用與受壓側應力集中因數相同的計算方法，對法蘭受拉應力集中處進行

圖13 法蘭受拉焊縫第一主應力圖

應力集中因數計算，得到受拉側焊縫和法蘭圓角處應力集中因數曲線，分別如圖14、圖15所示。

圖14 受拉側焊縫應力集中因數曲線

圖15 受拉側法蘭圓角處應力集中因數曲線

根據應力集中因數計算結果確認，隨著所加載荷逐漸增大，應力集中因數逐漸增大，但是圓角處應力集中因數大于焊縫處，說明焊縫處相比圓角處較安全。因此，在實際應用中，需要對法蘭倒角進行深入優化，強化法蘭的安全性能。

4 結論

根據對塔頂法蘭的理論分析，發現法蘭在彎矩作用下易發生壓縮和拉伸變形。針對不同變形進行應力分析，確認在彎矩作用下法蘭受拉側較受壓側受力大，受拉側間隙產生在兩法蘭外側，而受壓側間隙產生在兩法蘭內側。

進一步進行有限元分析，確認法蘭拉伸變形較壓縮變形大，且危險處圓角和焊縫處應力集中因數較大；無論是拉伸還是壓縮，法蘭圓角處應力集中因數均大于焊縫處；受壓法蘭應力集中因數隨載荷加載逐漸增大后趨于平穩，進一步說明法蘭受壓側相比受拉側較安全。可見，有限元模擬與理論分析一致。為增強法蘭抗疲勞強度，實際應用中需要提高圓角處強度，如采取增大圓角半徑、提高圓角處光滑度和增大圓角處法蘭厚度等方法。針對焊縫處應力集中，應采用焊縫加強條，并提高焊接效果。

[1] 朱仁勝，劉永梅，蔣東翔，等.基于MW級風力發電機塔架的有限元分析[J].機械設計與制造，2011（5）：104-106.

[2] 周宏麗.風力發電機組法蘭連接系統結構分析研究[D].重慶：重慶大學，2012.

[3]BURTON T.風能技術[M].武鑫，譯.北京：科學出版社，2007.

[4] 楊廣雪，謝基龍，周素霞.4D軸貨車焊接構架的疲勞強度分析方法[J].北京交通大學學報，2009，33（1）：24-27.

[5] 朱濤，高峰，張步良，等.汽車結構中焊縫疲勞壽命預估[J].汽車技術，2006（10）：37-40.

[6] 曹廣啟，陳恩，季劍.法蘭間隙對塔筒連接螺栓疲勞壽命的影響分析[J].裝備機械，2015（4）：25-29.

[7] 西北工業大學機械原理及機械零件教研室.機械設計[M].8版.北京:高等教育出版社，2006.

[8] 艾伯哈特，胡斌.現代接觸動力學[M].南京：東南大學出版社，2003.

[9] 王秋芬，黃方林，張劉剛.基于Ansys的大型風電機組偏航連接系統計算方法研究[J].機械強度，2011，33（4）：607-612.

[10]Germanischer Lloyd Industrial Services GmbH.Guideline for the Certification ofWind Turbines：Edition2010[S].