初中數(shù)學(xué)利用有理數(shù)和無理數(shù)的性質(zhì)解題探究

伍文玉

（湖南省永州市東安縣端橋鋪鎮(zhèn)中學(xué) 湖南永州 425000）

在初中數(shù)學(xué)中，學(xué)生們首先接觸到的就是實數(shù)，我們在學(xué)習(xí)的過程中，首先就要分清什么是有理數(shù)，什么是無理數(shù)。我們要分的清首先就要弄清楚有理數(shù)跟無理數(shù)的概念性質(zhì)，初中生總是對概念理解不明確從而造成了這種題目錯誤百出。畢竟這些題是我們考試總能碰到的問題，雖然是基礎(chǔ)性的問題但是學(xué)生們總出問題。筆者本文通過來講解有理數(shù)與無理數(shù)的性質(zhì)從而應(yīng)用解題。

一、有理數(shù)跟循環(huán)小數(shù)的理解跟運算

有理數(shù)的概念我們要先弄清楚，整數(shù)跟分?jǐn)?shù)我們都叫做有理數(shù)其中包含正整數(shù)、負(fù)整數(shù)、零、正分?jǐn)?shù)、負(fù)分?jǐn)?shù)。循環(huán)小數(shù)都可以轉(zhuǎn)化為分?jǐn)?shù)所以不管是有限循環(huán)小數(shù)還是無限循環(huán)小數(shù)都可以叫做有理數(shù)。例如1除以9得到的是0.1111111無限循環(huán)，也可稱作九分之一，分?jǐn)?shù)是有理數(shù)所以循環(huán)小數(shù)也是有理數(shù)。我們還要合理使用相反數(shù)、倒數(shù)和絕對值三項知識，因為弄清楚這些才方便我們計算，合理的解決問題。[1]

我們要熟練的運用有理數(shù)來計算問題。初中里的有理數(shù)運算跟我們小學(xué)里所學(xué)過的知識不同，我們不僅要算出數(shù)值的大小，還要弄清楚計算結(jié)果的符號。我們要合理的運用有理數(shù)來計算，做到熟練跟精確，使我們學(xué)習(xí)有理數(shù)跟無理數(shù)最重要的目的。他們是整個初中數(shù)學(xué)知識的基礎(chǔ)。我們要向運用有理數(shù)的性質(zhì)來進(jìn)行解題還要學(xué)會有理數(shù)的運算法則和有理數(shù)的運算律。要理清楚有理數(shù)加、減、乘、除與乘方五種運算法則。有理數(shù)的加法法則是根據(jù)計算時同號，計算時出現(xiàn)異號還有出現(xiàn)零的時候怎么計算，當(dāng)異號兩數(shù)相加時我們需要特別注意別弄混了，很容易算錯。這里就要求我們對絕對值得理解要深刻，搞不清楚絕對值這些完全不會的，所以不光是有理數(shù)的概念我們要學(xué)會，還要學(xué)會絕對值等利系列運算方法。

我們在進(jìn)行有理數(shù)運算時我們要先乘除后加減，保證運算方法正確，然后注意正負(fù)號絕對值，這樣我們才能保證自己解題的正確性。才能更好的運用到數(shù)學(xué)運算中。[2]

二、無理數(shù)跟無限不循環(huán)小數(shù)得概念跟運算

在初中數(shù)學(xué)涉及到無理數(shù)時，我們先推出的是計算根號2數(shù)值，然后發(fā)現(xiàn)他是無限不循環(huán)的小數(shù)，所有我們初步對無理數(shù)有了個認(rèn)識。我們在學(xué)習(xí)無理數(shù)時，我們需要注意很多知識點，比如說無限不循環(huán)小數(shù)稱為無理數(shù)的條件是要是小數(shù)，是無限不循環(huán)小數(shù)。有理數(shù)跟無理數(shù)是實數(shù)的組成部分使我們學(xué)習(xí)初中數(shù)學(xué)的重要基礎(chǔ)，如果沒有無理數(shù)就不能進(jìn)行數(shù)學(xué)的計算，不能解決我們的日常生活問題。在進(jìn)行無理數(shù)的學(xué)習(xí)時，我們必須先理解其基礎(chǔ)概念，才能熟練地運用到計算中去。老師在引導(dǎo)學(xué)生們學(xué)習(xí)時，要激發(fā)學(xué)生的興趣，調(diào)動學(xué)生們的思維性更好的理解無理數(shù)，從而在計算上不會出現(xiàn)問題。

我們可以給學(xué)生們講典故激發(fā)起他們的學(xué)習(xí)興趣。比如說2500多年前，古希臘有一位偉大的數(shù)學(xué)家畢達(dá)哥拉斯。在數(shù)學(xué)史上，畢達(dá)哥拉斯最厲害的地方就是發(fā)現(xiàn)了勾股定理。然后，希巴斯通過勾股定理，發(fā)現(xiàn)邊長為1的正方形，其對角線長度不是一個有理數(shù)。然后畢達(dá)哥拉斯一直認(rèn)為萬物兼數(shù)，他說說的數(shù)就是整數(shù)。所以在希巴斯提出他的發(fā)現(xiàn)之后，畢達(dá)哥拉斯不敢相信，原來世界上真的有其他數(shù)的存在。畢達(dá)哥拉斯無法承受自己的理論將被推翻，所以他決定只要是關(guān)于其他數(shù)的問題，只能在學(xué)派內(nèi)部討論，不能傳出去。但是希巴斯沒有根據(jù)老師的指令守住這個秘密，把他的發(fā)現(xiàn)告訴了世人。這使畢達(dá)哥拉斯非常生氣，所以他下令嚴(yán)懲希巴斯。希巴斯不得不逃出去，然后還是被人活捉，扔進(jìn)了大海。但是，真理是不會消失的，畢氏學(xué)派抹殺真理是無理的舉動。所以人們?yōu)榱思o(jì)念希巴斯這位為真理而獻(xiàn)身的人，就把不可通約的數(shù)取名為無理數(shù)，我們所知道的無理數(shù)就是這么來的。

例如把無理數(shù)在數(shù)軸上進(jìn)行表示，進(jìn)而幫助學(xué)生理解無理數(shù)，也能幫助學(xué)生進(jìn)一步的理解數(shù)軸的含義。如下圖在數(shù)軸上表示

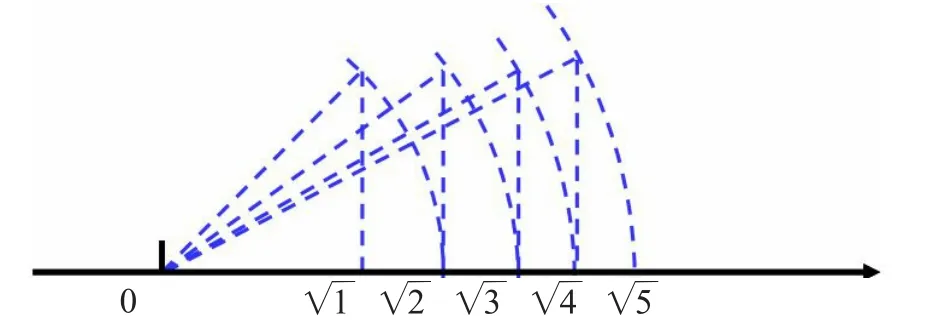
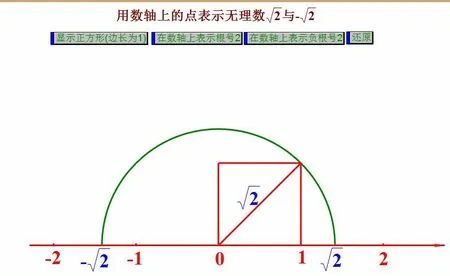
無理數(shù)的教學(xué)中，全新的知識點能激發(fā)學(xué)生的求知欲，還有很多學(xué)生因為遇到困難而放棄學(xué)習(xí)，我們首先就是要讓他們理清楚概念這樣在做題的時候才不會慌亂。首先要知道無理數(shù)這個概念有什么特點，然后再告訴他們在計算的時候可能遇到的問題，學(xué)生也需要把做題的時候遇到的問題及時向老師反饋。老師在教學(xué)的時候也要將無理數(shù)講得簡單易懂一點，這樣學(xué)生才不會畏懼才能更好的理解這個東西。在學(xué)習(xí)做題的時候，我們需要及時發(fā)現(xiàn)學(xué)生在做題時遇到的問題，還有學(xué)生特別困惑的地方要向老師提出來，這樣我們才能更好的在學(xué)習(xí)中做出反饋，更好的把這些教給學(xué)生。

三、概念性質(zhì)的理解教學(xué)

在概念教學(xué)中，老師要清楚地了解到學(xué)生有沒有理解這個概念跟性質(zhì)。學(xué)生在學(xué)習(xí)一個新的知識概念的時候一般是根據(jù)自己的認(rèn)知跟理解來學(xué)習(xí)的，但是一個新的概念有些時候跟以前接觸過的其他東西不同，所以這時候就需要我們教師需要引導(dǎo)學(xué)生理解概念，應(yīng)該依據(jù)學(xué)生概念學(xué)習(xí)的這種機制。學(xué)生理解后就能很好的運用進(jìn)行計算，從而我們就正確的運用了性質(zhì)進(jìn)行計算。

我們對性質(zhì)教學(xué)的完整過程，首先將性質(zhì)引導(dǎo)給學(xué)生然后讓學(xué)生記憶學(xué)習(xí)，只有這個樣子我們才能更好教會學(xué)生理解性質(zhì)從而運用到實際計算中。初中數(shù)學(xué)性質(zhì)概念具有層次性的特點。我們需要將他們形成一個好的體系然后系統(tǒng)的認(rèn)知。這樣學(xué)生對抽象的概念性質(zhì)的理解會提高，從而能更好的做題。

結(jié)語

在我們初中數(shù)學(xué)學(xué)習(xí)的過程中，在實數(shù)這一部分，對于有理數(shù)來說，無理數(shù)不能使用用分?jǐn)?shù)來表達(dá)。我們需要注意的是，我們在數(shù)學(xué)計算題中經(jīng)常會要求把結(jié)果通過四舍五入化為與準(zhǔn)確值有差異的近似數(shù)。這樣學(xué)生容易出現(xiàn)誤會，錯誤認(rèn)為分?jǐn)?shù)可以化為無限不循環(huán)小數(shù)。數(shù)學(xué)教師應(yīng)該多向?qū)W生強調(diào)，將某分?jǐn)?shù)化為小數(shù)時，要求約值的意義并非等同于把分?jǐn)?shù)化為小數(shù)。然后平時我們要加強反饋，告訴學(xué)生怎么去做題，總結(jié)做題的經(jīng)驗。只有我們先弄清楚有理數(shù)跟無理數(shù)的性質(zhì)，才能將它們區(qū)分，在計算的時候合理的解決問題，絕對值與正負(fù)號也是我們必須掌握的，這是輔助我們做題計算必備的知識，我們只有掌握了有理數(shù)跟無理數(shù)的性質(zhì)計算才能打好初中數(shù)學(xué)的基礎(chǔ)，學(xué)好初中數(shù)學(xué)。