關(guān)于Lagrange微分中值定理的應(yīng)用

王 鵬

（吉林省集安市第一中學(xué) 吉林集安 134200）

引言

Lagrange中值定理是研究函數(shù)在區(qū)間全體性質(zhì)的有力工具，是微分學(xué)的核心定理。所以一直備受人們的關(guān)注。但人們往往只注意定理的內(nèi)容，而對定理的應(yīng)用不是很靈活。本文針對Lagrange中值定理給出了幾個方面的應(yīng)用。

一、預(yù)備知識

函數(shù)在某一點的導(dǎo)數(shù)只反映了函數(shù)在局部或小范圍內(nèi)的性質(zhì)，但在實際問題中我們往往需要討論函數(shù)在全局或大規(guī)模范圍內(nèi)的性質(zhì)。特別是，有必要從函數(shù)的導(dǎo)數(shù)給出的局部性質(zhì)推導(dǎo)出其整體性質(zhì)或大規(guī)模性質(zhì)。所學(xué)的微分是用自變量的變化量和起點的導(dǎo)數(shù)值來表示函數(shù)變化的近似值。

然而，這只是一個近x似方程（一般說來，其誤差只在Δx→0時才趨向零），而且只在0附近可用，所以它不適用于解決所提出的問題。然而，這個精確的方程可以得到：只要在起點（1）的導(dǎo)數(shù)值f′(x0)被x0與x之間的某一點ξ的導(dǎo)數(shù)值f′(ξ)所取代。即

其理論根據(jù)就是Lagrange中值定理。

定理1 (Lagrange中值定理) 設(shè)函數(shù)f(x)滿足條件①f(x)在[a，b]上連續(xù)。②在(a，b)內(nèi)可導(dǎo)ξ，

則在(a，b)內(nèi)至少存在一點(a＜ξ＜b)，

推論2 如果f(x)在開區(qū)間(a，b)內(nèi)滿足f′(x)=0，那么在(a，b)內(nèi)f(x)=C.

主要描述函數(shù)在一定區(qū)間上的增量與函數(shù)在該區(qū)間上某一點上的導(dǎo)數(shù)之間的關(guān)系。因此，它也被稱為有限增量定理。因此，在研究函數(shù)的增量與導(dǎo)數(shù)的關(guān)系時，都可以用Lagrange中值定理來嘗試。

二、Lagrange中值定理的應(yīng)用

1.證明不等式

若函數(shù)f(x)滿足Lagrange中值定理的條件，則可得：

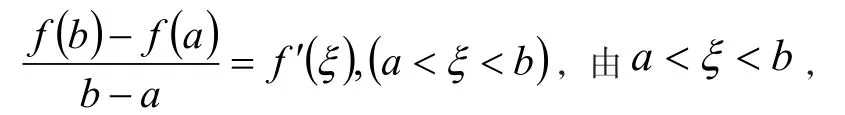
可得到f′(ξ)的一個取值范圍。從而這樣就有了一個值的范圍，對應(yīng)于不等式，這是使用Lagrange中值定理證明不等式的基礎(chǔ)。

因此，當(dāng)Lagrange中值定理用來證明不等式時，應(yīng)首先分析不等式，不等式變形，然后選擇函數(shù)和區(qū)間。將不等式的一邊，使函數(shù)在某個區(qū)間上的函數(shù)增量與自變量增量的比值，再對該區(qū)間上的函數(shù)使用Lagrange中值定理。最后估值，即得所證不等式。

2.證明恒等式

在利用Lagrange中值定理證明恒等式時有以下兩種類型。

（1）等式兩端都為代數(shù)式

例1

如函數(shù)f(x)是[a，b]上的正值可微函數(shù)，則有ξ(a＜ξ＜b)使

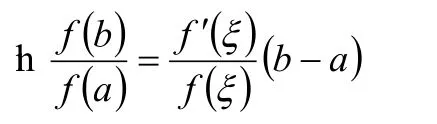
證 設(shè)φ(u)=lnf(u)，在[a，b]上。

由題設(shè)容易知道，φ(u)在[a，b]上滿足Lagrange中值定理的條件，故存在ξ∈(a，b)

這類題型直接從定理本身出發(fā)。分析等式，經(jīng)過變形，找到滿足Lagrange中值定理條件的增量函數(shù)，應(yīng)用Lagrange中值定理，再經(jīng)過變形得出所要證明的恒等式。

（2）等式的一端是一常數(shù)

證 設(shè)f(x)=arctgx+ar′cctgx，

則f′(x)=(arctgx+arcctgx)

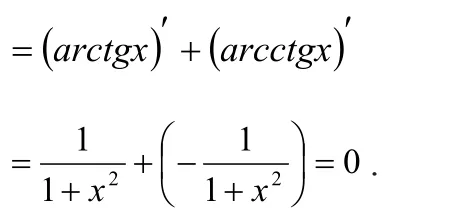
由Lagrange中值定理的推論知f(x)=c.

做這類題時，首先應(yīng)該設(shè)等式的一端為函數(shù)f(x)，然后對函數(shù)求導(dǎo)，若是能夠得出f′(x)=0。則應(yīng)用Lagrange中值定理，推出f(x)=C，因C為一常數(shù)，故任取一值代入等式左端，所得的值為定值C，所以恒等式得證。

3.研究函數(shù)在區(qū)間上的性態(tài)

由預(yù)備知識，根據(jù)已學(xué)過的微分，自變量在函數(shù)中某一點的變化量和x0與x之間某點ξ處的導(dǎo)數(shù)值f′(ξ)有如下關(guān)系f(x)-f(x0)=f′(ξ)(x-x0)，將其變形得到f(x)=f′(ξ)(x-x0)+f(x0)于是，轉(zhuǎn)化成了利用在ξ一點處的導(dǎo)數(shù)研究函數(shù)在整個區(qū)間上的性質(zhì)。

因此，在研究函數(shù)在區(qū)間上的性態(tài)時，首先根據(jù)題設(shè)找出滿足Lagrange中值定理條件的函數(shù)，然后應(yīng)用Lagrange中值定理，得出恒等式，再由題設(shè)條件推出函數(shù)導(dǎo)數(shù)與零的關(guān)系，從而證明出所求區(qū)間的性態(tài)。

4.證明方程根的存在性

例3 設(shè)f(x)在(a，+∞)上連續(xù)，且當(dāng)x＞a時，有f′(x)＞1，證明，如果f(a)＜0，則方程f(x)=0在(a，a-f(a))上有且只有一個實根。

證 存在性，由題設(shè)知，函數(shù)f(x)在[a，a-f(a)]上連續(xù)，在(a，a-f(a))上可導(dǎo)，根據(jù)Lagrange中值定理，在(a，a-f(a))內(nèi)至少存在一點ξ使

f(a-f(a))-f(a)=f′(ξ)[(a-f(a))-a]，a＜ξ＜a-f(a)成立

亦f(a-f(a))=f(a)-f(ξ)f(a).

因f(a)＜0，f′(ξ)＞1

有f(a-f(a))=[-f(a)][f′(ξ)-1]＞0.

從而f(a)?f(a-f(a))＜0，根據(jù)連續(xù)函數(shù)的介值定理知，在區(qū)間(a，a-f(a))內(nèi)至少存在一點ξ，使f(ξ)=0成立，即方程f(x)=0在(a，a-f(a))內(nèi)至少有一個實根。

唯一性，因f′(x)＞1＞0，函數(shù)f(x)在[a，a-f(a)]上單調(diào)增加，從而知f(x)=0在(a，a-f(a))內(nèi)有且僅有一個實根。