走滑斷層作用下X80管道設(shè)計(jì)應(yīng)變規(guī)律和神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)*

鄭　倩，張　宏，張克政，劉嘯奔，夏夢(mèng)瑩，吳　鍇，王寶棟

(1. 中國(guó)石油大學(xué)(北京) 機(jī)械與儲(chǔ)運(yùn)工程學(xué)院，北京 102249；2. 中海石油氣電集團(tuán)有限責(zé)任公司，北京 100028)

0　引言

活動(dòng)斷層是管道穿越地震區(qū)的主要威脅，斷層作用下管道會(huì)因較大的應(yīng)變而失效。因此，預(yù)測(cè)管道在斷層作用下的應(yīng)變對(duì)跨斷層區(qū)管道的設(shè)計(jì)與安全評(píng)估具有重要意義[1]。

在斷層下管道響應(yīng)研究領(lǐng)域，Newmark-Hall法、Kennedy法和Karomitros法是較具代表性的解析方法。前2種方法均采用“索”模型來(lái)模擬管道[2-3]，管道只能承受軸向的拉伸而不能承受側(cè)向的彎矩，因此只能在穿越角小且斷層位移較大(即管道主要受軸向拉伸)時(shí)才能得到比較準(zhǔn)確的結(jié)果[4]。而Karamitros法考慮了管道剛度的變化，采用彈性梁-彈性地基梁模型可較準(zhǔn)確地計(jì)算出走滑斷層下管道受拉時(shí)的設(shè)計(jì)應(yīng)變[4-5]。由于解析方法中基本假設(shè)的局限性，有限元方法被更加廣泛地用于準(zhǔn)確計(jì)算管道的各種力學(xué)響應(yīng)，并根據(jù)其計(jì)算結(jié)果開(kāi)展管道力學(xué)響應(yīng)規(guī)律的分析[6]。劉嘯奔等[7]基于非線(xiàn)性有限元軟件，利用管單元 -彎管單元計(jì)算了X80管道穿越走滑斷層時(shí)的最大壓應(yīng)變，提出了半經(jīng)驗(yàn)應(yīng)變預(yù)測(cè)模型。

解析法的計(jì)算較為快捷，但準(zhǔn)確性不高，且只能適用于管道受拉伸情況，對(duì)于管道壓縮時(shí)完全不適用，也無(wú)法分析管道的屈曲行為。有限元法因計(jì)算結(jié)果的準(zhǔn)確性而得到廣泛應(yīng)用，但該方法計(jì)算時(shí)間長(zhǎng)，對(duì)計(jì)算機(jī)硬件要求高，且建模過(guò)程也較復(fù)雜。2013年，SHOKOUHI等[8]將神經(jīng)網(wǎng)絡(luò)用于地震作用下管道應(yīng)變的計(jì)算，該方法基于限元模型的計(jì)算結(jié)果對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，訓(xùn)練好的網(wǎng)絡(luò)可準(zhǔn)確預(yù)測(cè)管道的應(yīng)變，但其有限元模型中并未準(zhǔn)確考慮土壤特性參數(shù)對(duì)管道應(yīng)變的影響，因此與真實(shí)工況會(huì)有一定誤差；李劍楠[9]將神經(jīng)網(wǎng)絡(luò)用于埋地管道的可靠性分析中，利用神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)了斷層場(chǎng)地下管道的最大軸向應(yīng)力值，但其訓(xùn)練樣本中最大軸向應(yīng)力值并非通過(guò)計(jì)算準(zhǔn)確的有限元法獲得，而是利用Newmark-Hall解析方法計(jì)算而來(lái)，而目前的有限元計(jì)算已表明，Newmark-Hall法在管道穿越角度較大時(shí)的結(jié)果過(guò)于不保守。因此，該網(wǎng)絡(luò)模型的預(yù)測(cè)結(jié)果具有局限性。人工神經(jīng)網(wǎng)絡(luò)具有高度非線(xiàn)性運(yùn)算能力，能對(duì)復(fù)雜的數(shù)學(xué)模型進(jìn)行預(yù)測(cè)，是解決隱式問(wèn)題的有效方法，被廣泛應(yīng)用于多個(gè)領(lǐng)域。在管道方面，神經(jīng)網(wǎng)絡(luò)多用于管道腐蝕問(wèn)題的研究，多數(shù)學(xué)者均采用神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)管道的腐蝕速率[10]、腐蝕剩余強(qiáng)度[11]及其爆破壓力[12]等，而利用神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)管道在地質(zhì)災(zāi)害作用下的應(yīng)變較少。基于此，本文以走滑斷層下的X80管道為研究對(duì)象，建立了管道應(yīng)力應(yīng)變計(jì)算的有限元模型；分析了管徑、壁厚、內(nèi)壓、斷層位移以及土彈簧極限抗力對(duì)管道軸向最大拉、壓應(yīng)變的影響；基于數(shù)值計(jì)算結(jié)果，采用神經(jīng)網(wǎng)絡(luò)建立起管道設(shè)計(jì)應(yīng)變的預(yù)測(cè)模型。

1　走滑斷層下管道的有限元模型

圖1為管道穿越走滑斷層的示意圖，斷層引起地表錯(cuò)動(dòng)從而導(dǎo)致管道發(fā)生變形，如圖1所示，管道穿越角β為90°，管道的軸向?yàn)閤方向，側(cè)向?yàn)閥方向，管道在該斷層下主要受到拉伸和彎曲作用。

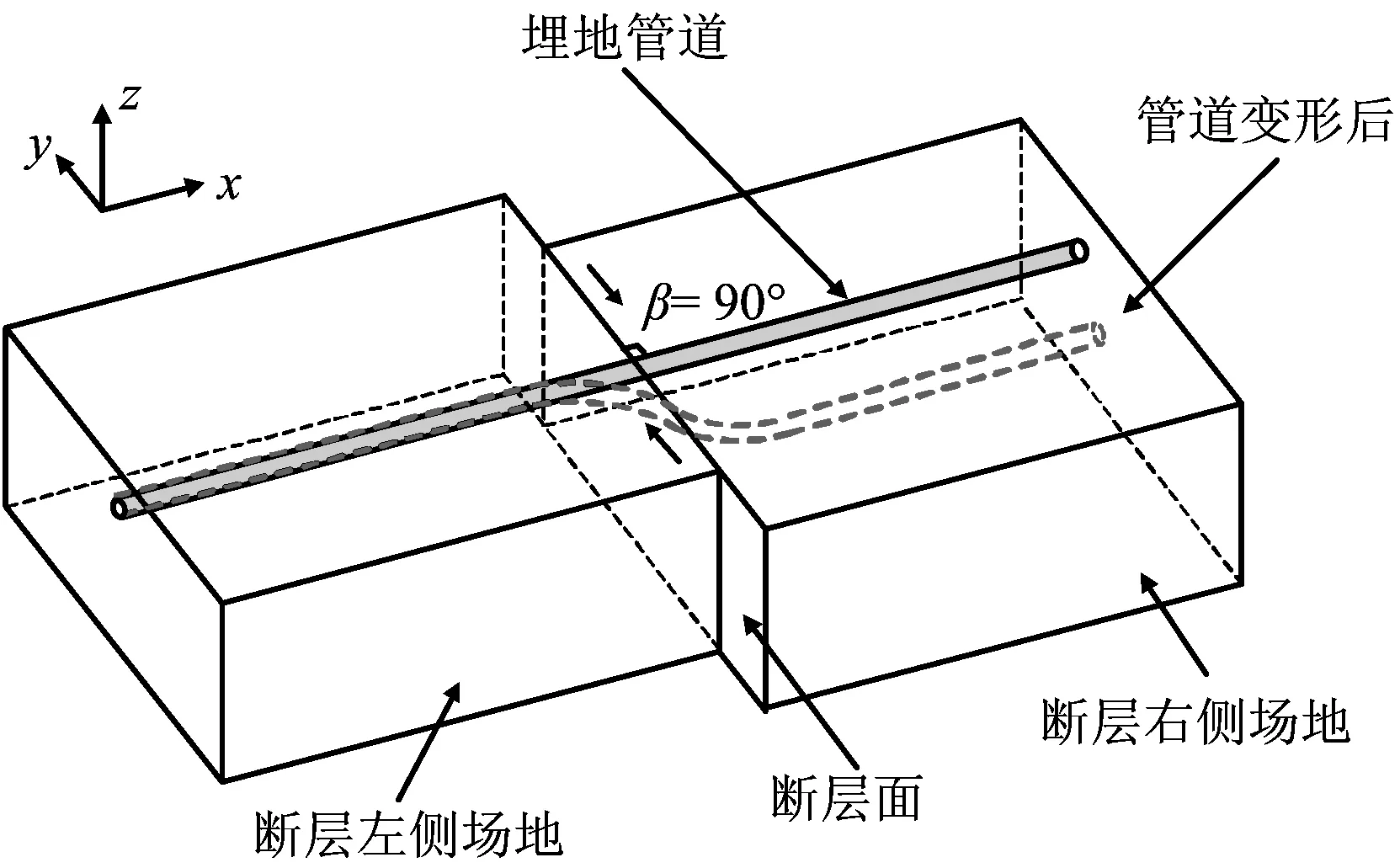
圖1　管道穿越斷層示意Fig.1　Sketch of pipe subjected to strike-slip fault displacement.

為準(zhǔn)確模擬斷層附近管道的力學(xué)響應(yīng)，本文采用ABAQUS軟件提供的Jointc單元來(lái)模擬土彈簧，采用管殼耦合的方式建立了對(duì)應(yīng)的有限元模型。模型中管道分為2部分，管道總長(zhǎng)取2 100 m，利用殼單元模擬斷層兩側(cè)100 m范圍內(nèi)管道，環(huán)向分為24個(gè)節(jié)點(diǎn)，沿軸向每0.2 m 1個(gè)單元；剩余部分管道采用管單元模擬，每1 m 1個(gè)單元，使用耦合單元將管單元和殼單元連接起來(lái)，各向土彈簧與單元節(jié)點(diǎn)相連，圖2為本文有限元模型的示意圖。

Ramberg-Osgood模型能較好地描述高強(qiáng)鋼管道的力學(xué)性能[9]，用該模型對(duì)X80鋼管材料拉伸實(shí)驗(yàn)結(jié)果的應(yīng)力-應(yīng)變曲線(xiàn)進(jìn)行擬合，得到如表1所示的擬合參數(shù)。

表1　X80管材特性取值

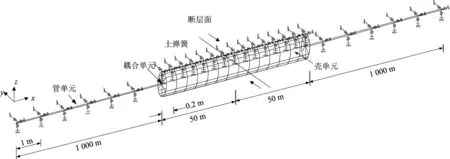
圖2　走滑斷層下有限元模型示意Fig.2　Simplified FE model of a pipeline crossing a strike-slip fault

2　參數(shù)分析

本文主要參考西二線(xiàn)工程確定各參數(shù)取值，部分參數(shù)取值范圍如表2所示。同時(shí)結(jié)合我國(guó)國(guó)情需要，補(bǔ)充了外徑為1 422 mm管道的相關(guān)參數(shù)。

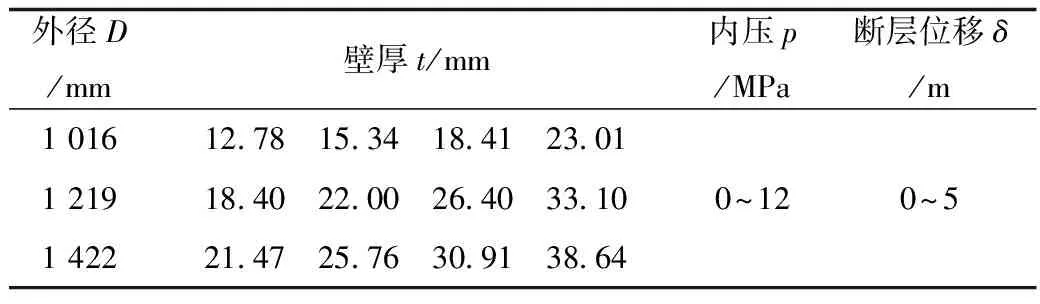
表2　影響因素的取值范圍

走滑斷層下，僅軸向、側(cè)向土彈簧會(huì)對(duì)管道產(chǎn)生作用力。參數(shù)分析中，考慮軸向、側(cè)向土彈簧極限抗力取值的相關(guān)性，從而保證計(jì)算所用的土壤極限抗力的范圍更貼近實(shí)際工況。根據(jù)ALA-ASCE 2001附錄B中推薦的公式，采用表3中砂土的土壤參數(shù)，計(jì)算得到工程中管道可能受到的土彈簧軸向和側(cè)向土彈簧極限抗力的取值范圍如圖3所示。

表3　砂土特性參數(shù)取值范圍

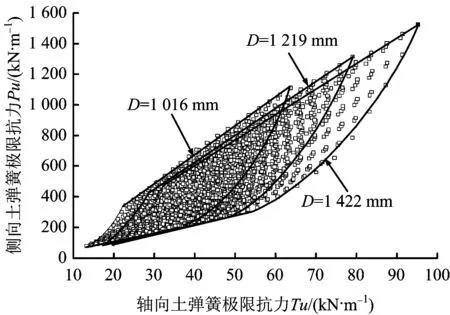
圖3　軸向和側(cè)向土彈簧極限抗力取值范圍Fig.3　Range of Tu and Pu

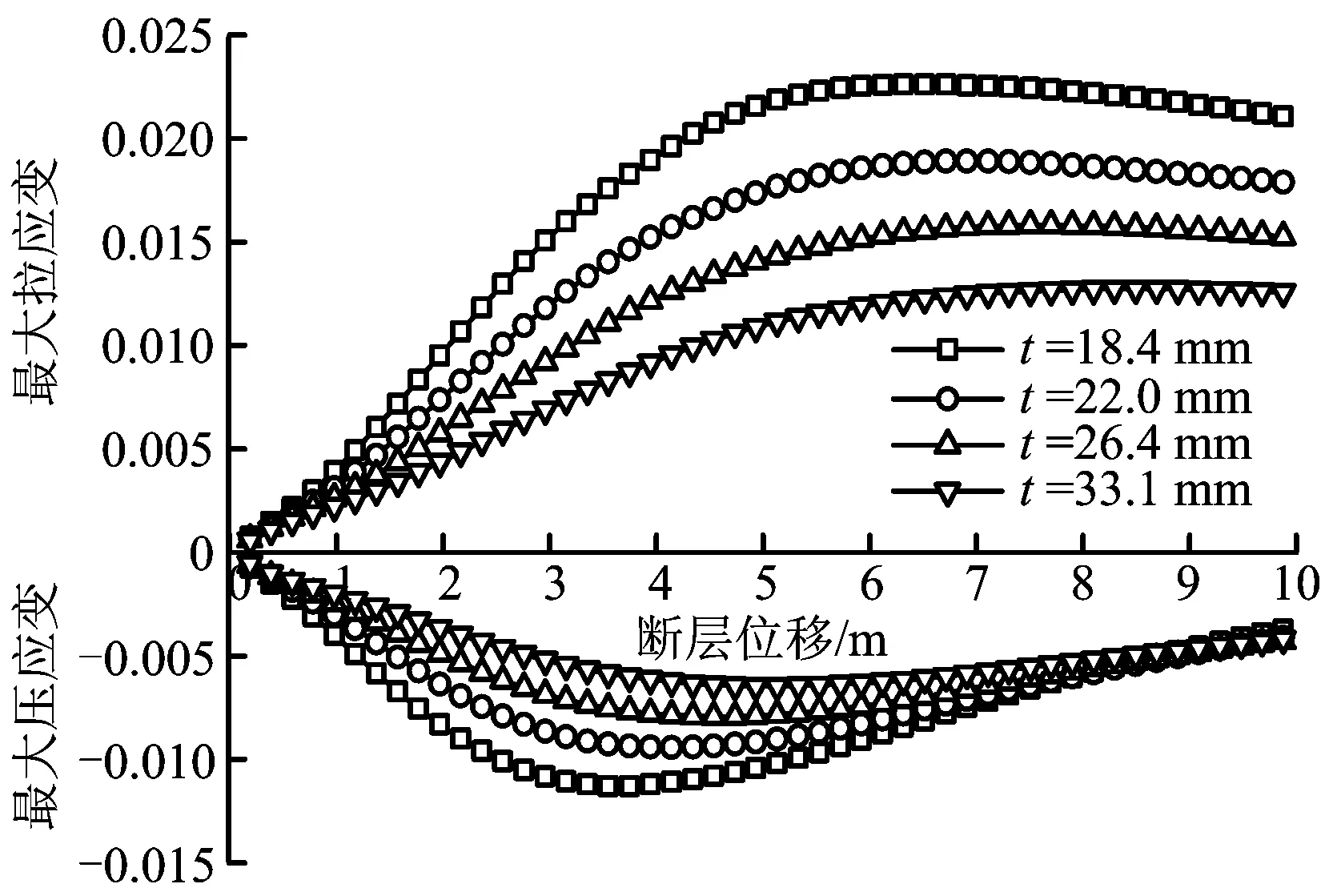
圖4　不同壁厚下設(shè)計(jì)應(yīng)變隨斷層位移的變化規(guī)律(φ 1 219 mm)Fig.4　Relationship between design strain and fault displacement with different pipe wall thicknesses(φ 1 219 mm)

2.1　管徑和壁厚的影響

圖4為φ 1 219 mm管道的設(shè)計(jì)應(yīng)變?cè)诓煌诤裣码S斷層位移的變化規(guī)律。圖4顯示，壁厚越大，在同一斷層位移下的設(shè)計(jì)應(yīng)變?cè)叫　Ｒ虼耍诤竦脑龃笥兄诠艿揽拐稹５畲罄瓚?yīng)變與最大壓應(yīng)變隨斷層位移變化的趨勢(shì)不同，斷層位移增大時(shí)，最大拉應(yīng)變呈“逐漸增長(zhǎng)→趨于平緩→逐漸減小”的趨勢(shì)，而最大壓應(yīng)變呈“逐漸增長(zhǎng)→逐漸減小”的變化，且壁厚越大，設(shè)計(jì)應(yīng)變峰值越小，設(shè)計(jì)應(yīng)變平緩段越長(zhǎng)。在同一斷層位移下，管道的最大拉應(yīng)變總是高于最大壓應(yīng)變。因此，在穿越角為90°的走滑斷層下，管道主要受到拉伸作用。

管道設(shè)計(jì)應(yīng)變由軸心應(yīng)變與彎曲應(yīng)變控制。斷層位移較小時(shí)，管道彎曲應(yīng)變較大，軸心應(yīng)變幾乎為零。隨著斷層位移的增加，管道整體呈伸長(zhǎng)趨勢(shì)，在協(xié)調(diào)條件下，管道軸心應(yīng)變逐漸增大。隨著斷層位移的進(jìn)一步增加，管道彎曲段的曲率幾乎不變，此時(shí)彎曲應(yīng)變較小，而更多管道進(jìn)入彎曲段，軸心應(yīng)變逐漸降低。因此，導(dǎo)致整個(gè)管道的最大拉應(yīng)變逐漸變小。同小壁厚管道相比，相同外徑下的大壁厚管道的彎曲剛度和軸向剛度均增加，因此，具有更強(qiáng)的抵抗變形的能力，在應(yīng)變規(guī)律上體現(xiàn)出具有更小的設(shè)計(jì)應(yīng)變峰值和更長(zhǎng)的應(yīng)變平緩段。

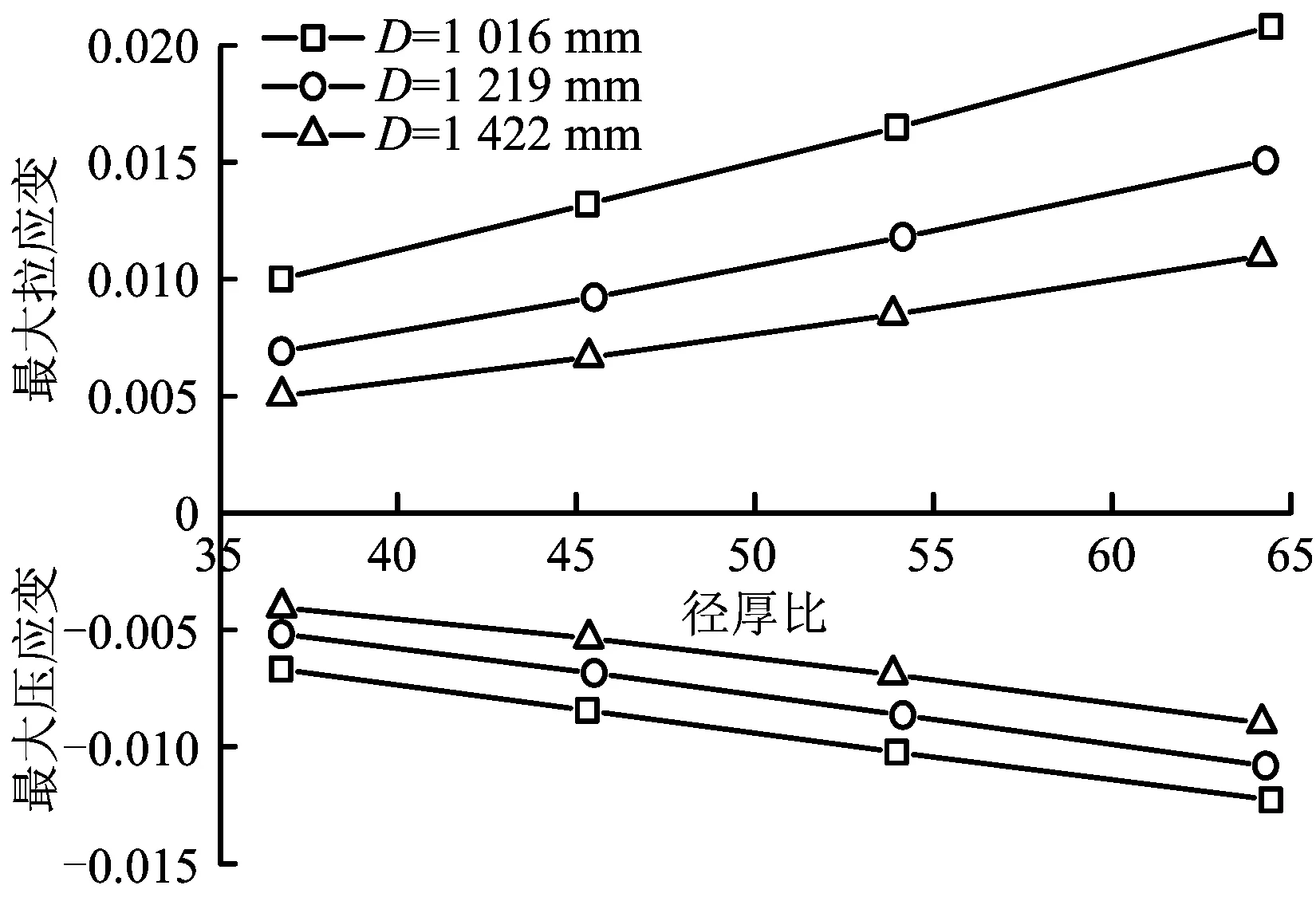
圖5　不同管徑下設(shè)計(jì)應(yīng)變隨徑厚比的變化規(guī)律(δ=3 m)Fig.5　Relationship between design strain and D/t with different pipe diameters(δ=3 m)

圖5為設(shè)計(jì)應(yīng)變與徑厚比的關(guān)系，從該圖中可定性分析管徑對(duì)設(shè)計(jì)應(yīng)變的影響。圖5顯示，在徑厚比相等的情況下，管徑越大，設(shè)計(jì)應(yīng)變?cè)叫　Ｒ虼耍啥ㄐ苑治龅么蠊軓降目拐鹉芰Ω鼜?qiáng)，且設(shè)計(jì)應(yīng)變與徑厚比近似呈線(xiàn)性關(guān)系。

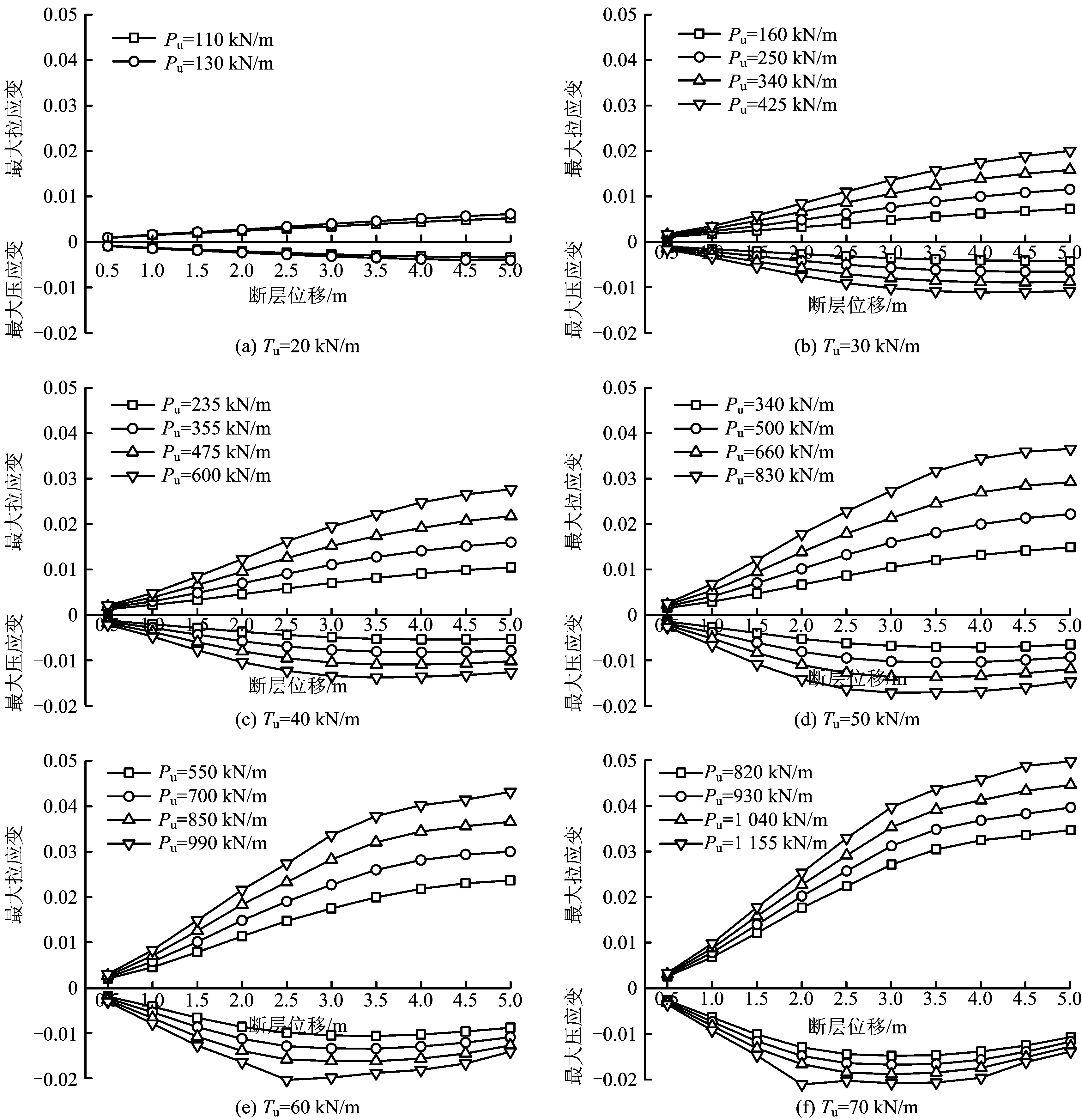
圖7　不同土彈簧極限抗力下設(shè)計(jì)應(yīng)變隨斷層位移的變化規(guī)律(φ 1 219 mm×22 mm)Fig. 7　Relationship between design strain and fault displacement with different ultimate resistance of soil springs(φ 1 219 mm×22 mm)

2.2　內(nèi)壓的影響

根據(jù)表2給出的內(nèi)壓范圍，以φ 1 219 mm × 22 mm管道為例分析內(nèi)壓對(duì)設(shè)計(jì)應(yīng)變的影響。內(nèi)壓取值為0，2，4，6，8，10和12 MPa，分析結(jié)果如圖6所示。圖6顯示，管道的設(shè)計(jì)應(yīng)變隨內(nèi)壓的增大而增大，但內(nèi)壓對(duì)應(yīng)變的影響并不顯著，甚至在小位移下(δ≤1 m)，內(nèi)壓對(duì)管道的設(shè)計(jì)應(yīng)變幾乎無(wú)影響。

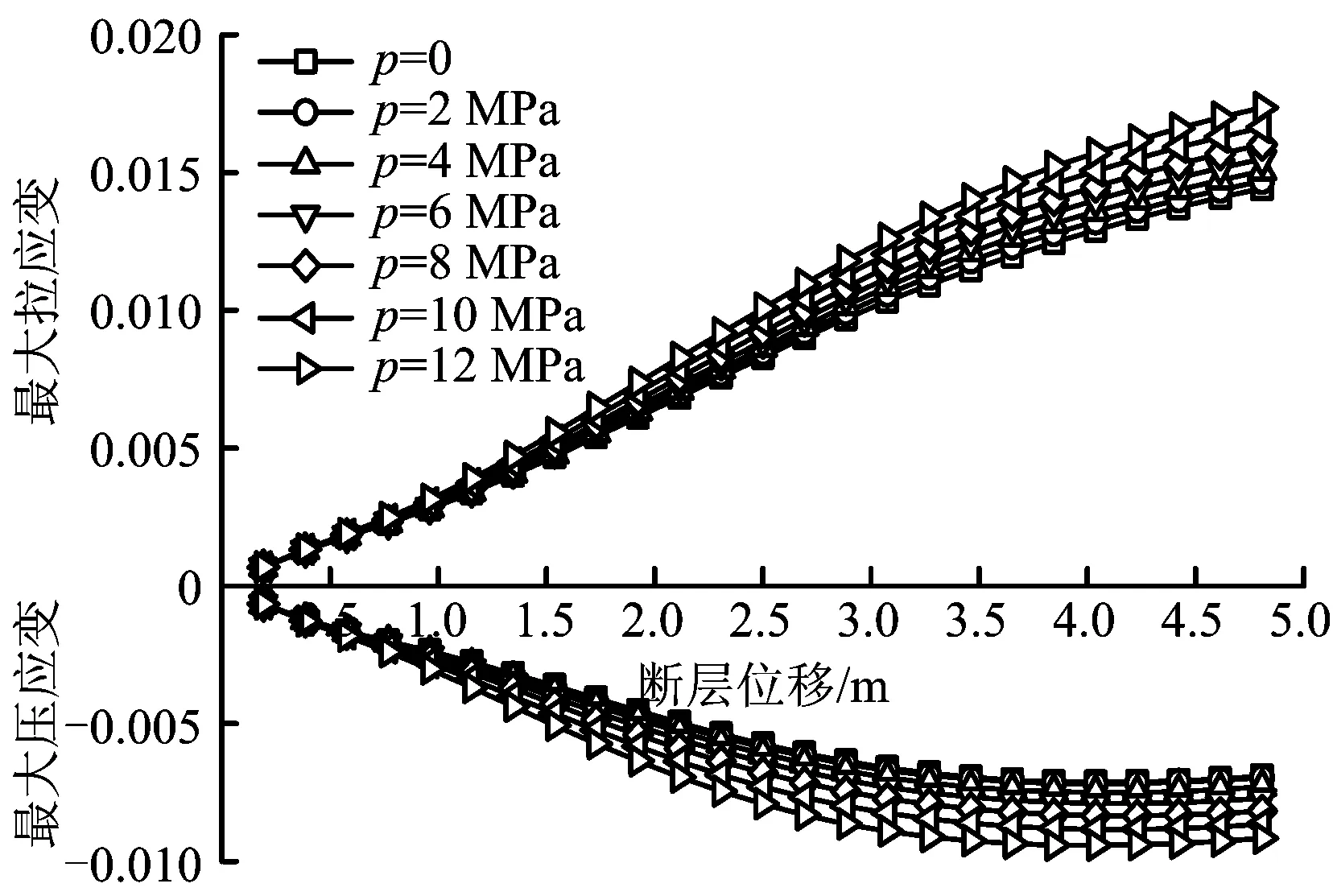
圖6　不同內(nèi)壓下設(shè)計(jì)應(yīng)變隨斷層位移的變化規(guī)律Fig. 6　Relationship between design strain and fault displacement with different internal pressures

2.3　土壤的影響

根據(jù)圖3中確定的土彈簧極限抗力范圍，得到如圖7所示的不同土彈簧極限抗力組合下設(shè)計(jì)應(yīng)變隨斷層位移的變化規(guī)律。

當(dāng)軸向土彈簧極限抗力相等時(shí)，在相同斷層位移下，側(cè)向土彈簧極限抗力越大，設(shè)計(jì)應(yīng)變也越大。這是因?yàn)橥翉椈蓸O限抗力越大，在相同斷層位移下，土壤對(duì)管道的作用力就越大，因而設(shè)計(jì)應(yīng)變也越大，越不利于管道抗震。

3　BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)

人工神經(jīng)網(wǎng)絡(luò)技術(shù)是對(duì)大腦功能的模擬、抽象和簡(jiǎn)化[13]，具有學(xué)習(xí)、聯(lián)想和記憶功能，以及高度的非線(xiàn)性預(yù)測(cè)能力。BP神經(jīng)網(wǎng)絡(luò)屬于多層前饋網(wǎng)絡(luò)，網(wǎng)絡(luò)訓(xùn)練時(shí)信號(hào)前向傳遞，誤差反向傳播，根據(jù)預(yù)測(cè)誤差，采用梯度下降法調(diào)整網(wǎng)絡(luò)的權(quán)值和閾值，使預(yù)測(cè)輸出不斷逼近期望輸出[14]。本文利用BP雙隱層神經(jīng)網(wǎng)絡(luò)對(duì)走滑斷層下穿越角為90°的X80管道的設(shè)計(jì)應(yīng)變進(jìn)行預(yù)測(cè)，雙隱層網(wǎng)絡(luò)包含2個(gè)單隱層，同單隱層相比，多隱層網(wǎng)絡(luò)具有更強(qiáng)的泛化能力和更高的預(yù)測(cè)精度[15]。

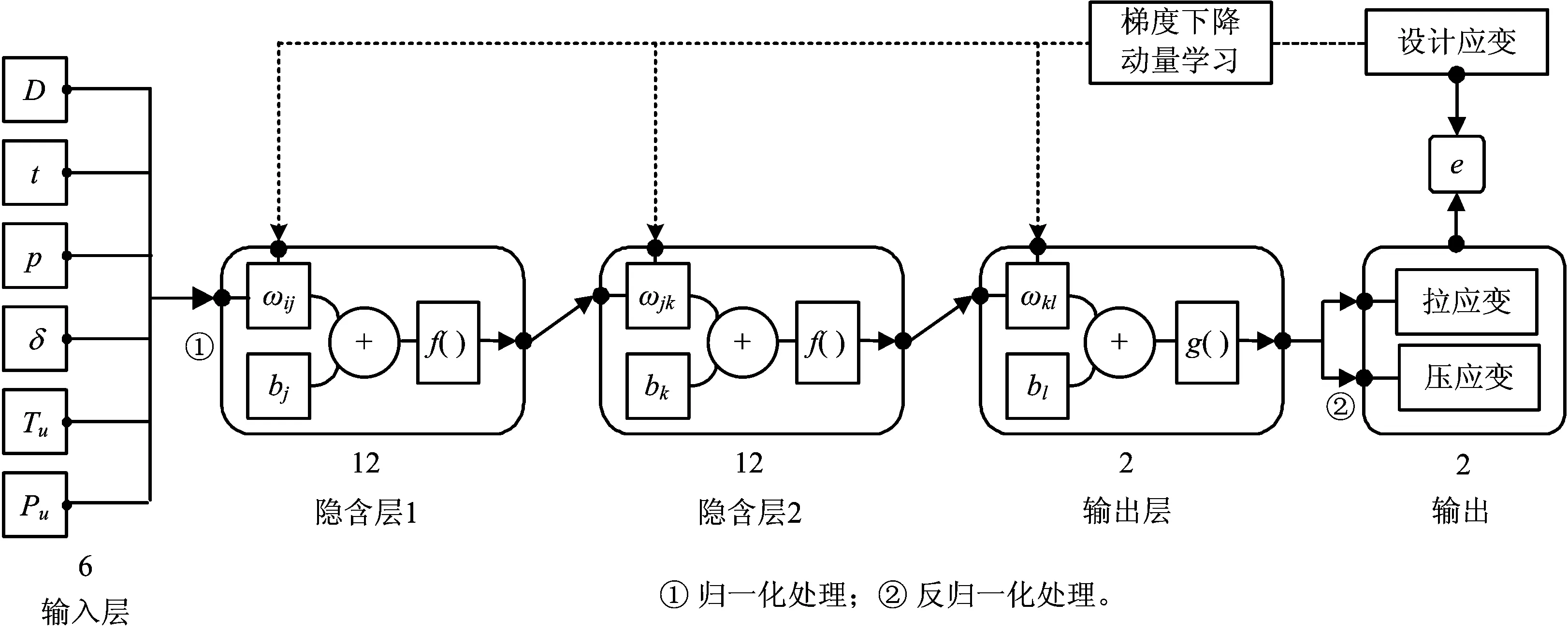
圖8　BP雙隱層神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)Fig. 8　The structure of BP double hidden layer neural network

為了全面分析管徑、壁厚以及內(nèi)壓因素對(duì)設(shè)計(jì)應(yīng)變的影響，在第2.1節(jié)和第2.2節(jié)計(jì)算工況總數(shù)為3×4×7×25=2 100個(gè)(其中，3指管徑取3個(gè)值；4指每個(gè)管徑下的壁厚取4個(gè)值；7指內(nèi)壓取7個(gè)值；25為斷層位移取25個(gè)值)，包括了X80所有管道在不同內(nèi)壓和斷層位移條件下的工況。

在分析土彈簧極限抗力對(duì)設(shè)計(jì)應(yīng)變的影響時(shí)，為減少計(jì)算成本，斷層位移設(shè)定為10個(gè)，且由第2.2節(jié)分析可得，內(nèi)壓對(duì)管道設(shè)計(jì)應(yīng)變的影響很小。因此，內(nèi)壓設(shè)定為12 MPa。該項(xiàng)分析中，算例總數(shù)為(20+23+25)×4×1×10=2 720(其中，20，23，25分別為指管徑為1 016 mm，1 219 mm，1 422 mm的土彈簧極限抗力組合取值個(gè)數(shù)；4指各管徑下的壁厚分別取4個(gè)值；1為內(nèi)壓取1個(gè)值，內(nèi)壓值為12 MPa；10是指斷層位移取10個(gè)值)，包括了X80不同管道在不同斷層位移條件下的工況。由此可知，以上參數(shù)計(jì)算包含了X80管道在不同內(nèi)壓、不同斷層位移以及不同軸向、側(cè)向土彈簧極限抗力組合條件下的工況，因此，該數(shù)據(jù)庫(kù)涵蓋了多因素影響下的工況，能對(duì)神經(jīng)網(wǎng)絡(luò)進(jìn)行充分的訓(xùn)練。

3.1　網(wǎng)絡(luò)的結(jié)構(gòu)和訓(xùn)練

根據(jù)走滑斷層下管道破壞原因，在穿越角為90°時(shí)，影響X80管道的應(yīng)變因素主要包括管徑(D)、壁厚(t)、內(nèi)壓(p)、斷層位移(δ)、軸向土彈簧極限抗力(Tu)及側(cè)向土彈簧極限抗力(Pu)等6個(gè)因素。因此，將其作為網(wǎng)絡(luò)輸入層的6個(gè)神經(jīng)元。將最大拉應(yīng)變(εTmax)和最大壓應(yīng)變(εCmax)作為輸出層的2個(gè)神經(jīng)元。隱含層個(gè)數(shù)根據(jù)式(1)初步確定[16]：

(1)

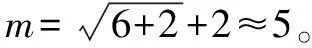
網(wǎng)絡(luò)隱含層傳遞函數(shù)選用雙曲正切S型傳遞函數(shù)tansig，該函數(shù)將輸出控制在[-1,1]范圍內(nèi)，可將數(shù)據(jù)統(tǒng)一成一個(gè)量級(jí)，避免了計(jì)算中不必要的數(shù)值問(wèn)題；輸出層采用線(xiàn)性傳遞函數(shù)purelin[17]。訓(xùn)練函數(shù)選用trainlm，即Levenberg-Marquardt優(yōu)化算法，該算法兼具牛頓法和共軛梯度法的優(yōu)點(diǎn)，能夠加快網(wǎng)絡(luò)的收斂速度[18]。

按照以上設(shè)定，采用MATLAB編程創(chuàng)建網(wǎng)絡(luò)。網(wǎng)絡(luò)的訓(xùn)練樣本總數(shù)為4 817組(有限元工況總數(shù)4 820與計(jì)算不收斂組數(shù)3的差值)，網(wǎng)絡(luò)結(jié)構(gòu)如圖8所示。經(jīng)過(guò)多次訓(xùn)練和計(jì)算，最終確定回歸效果最優(yōu)的網(wǎng)絡(luò)，此時(shí)網(wǎng)絡(luò)的回歸系數(shù)為0.999 92，說(shuō)明網(wǎng)絡(luò)訓(xùn)練后的預(yù)測(cè)效果良好。根據(jù)Kolmogrov定理，網(wǎng)絡(luò)節(jié)點(diǎn)數(shù)確定為12。

因此，網(wǎng)絡(luò)最終結(jié)構(gòu)為6-12-12-2，訓(xùn)練最大步數(shù)50，訓(xùn)練速率0.1，誤差平方和2×10-5。樣本總體數(shù)據(jù)的訓(xùn)練效果如圖9所示。

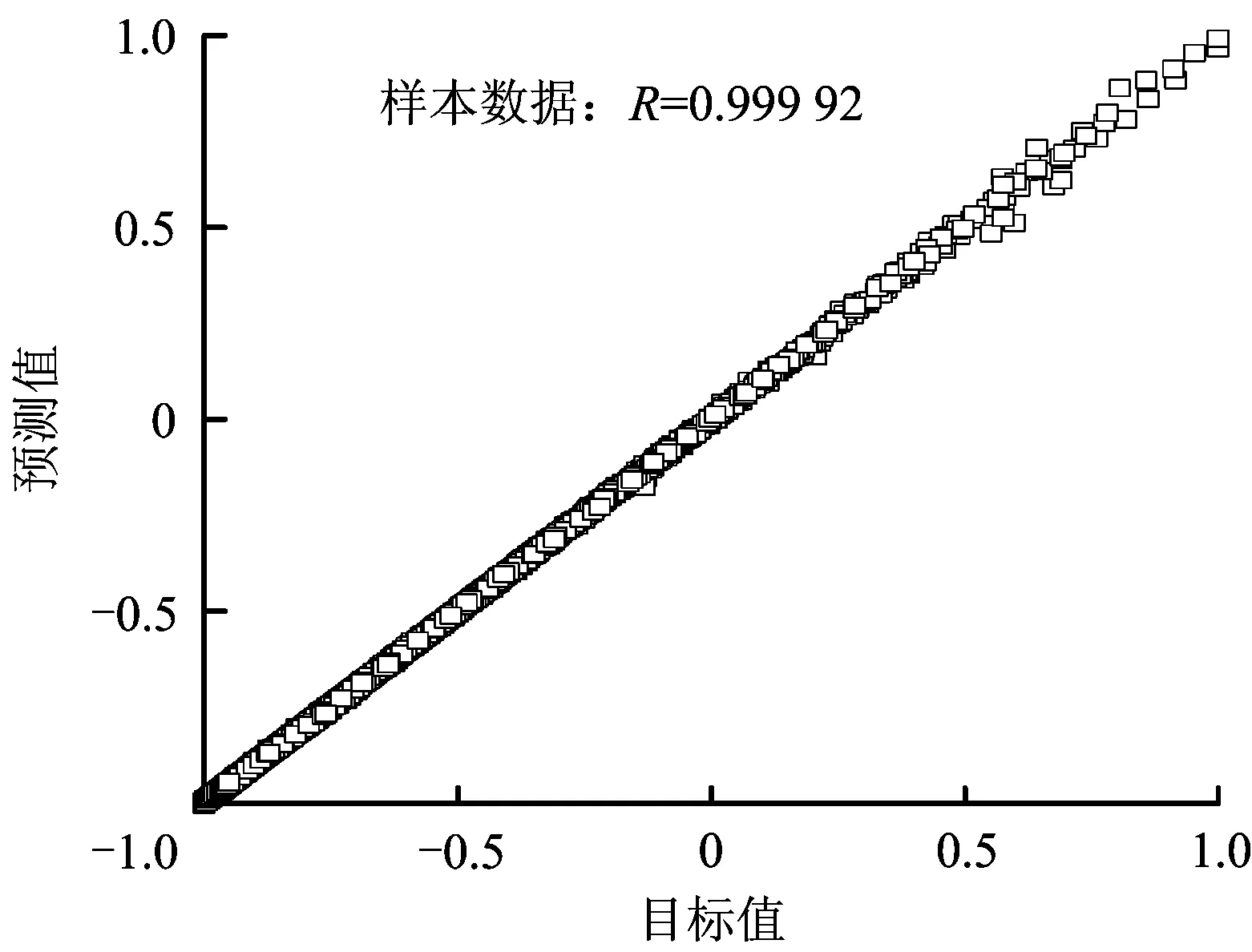
圖9　網(wǎng)絡(luò)訓(xùn)練結(jié)果Fig 9　The results for network training

3.2　神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)效果的驗(yàn)證

為驗(yàn)證網(wǎng)絡(luò)預(yù)測(cè)的準(zhǔn)確性，采用訓(xùn)練樣本以外的20組數(shù)據(jù)代入網(wǎng)絡(luò)進(jìn)行預(yù)測(cè)，預(yù)測(cè)樣本中各物理量除管徑、壁厚外，其他各參數(shù)應(yīng)隨機(jī)取值，取值既不與訓(xùn)練樣本數(shù)據(jù)相同，又滿(mǎn)足實(shí)際工況的要求。圖10為該20個(gè)樣本的網(wǎng)絡(luò)預(yù)測(cè)結(jié)果。

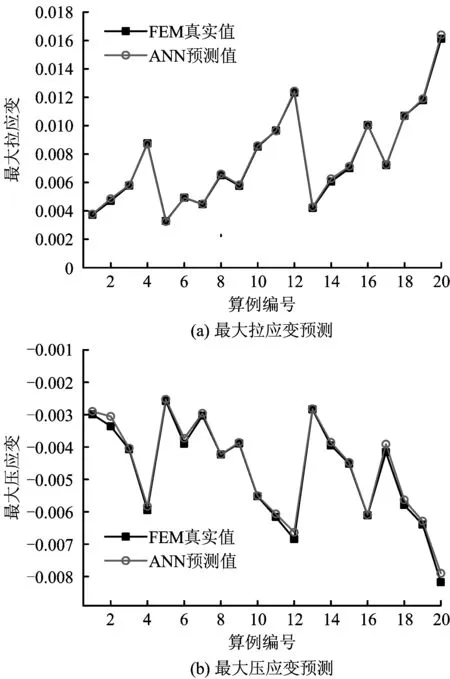
圖10　神經(jīng)網(wǎng)絡(luò)的預(yù)測(cè)結(jié)果Fig. 10　The results for predictions of neural network

圖10顯示，網(wǎng)絡(luò)預(yù)測(cè)值與真實(shí)值之間相差較小，且預(yù)測(cè)結(jié)果和真實(shí)結(jié)果的變化趨勢(shì)相同，表示該神經(jīng)網(wǎng)絡(luò)模型得到充分的訓(xùn)練，其中，最大拉應(yīng)變預(yù)測(cè)的相對(duì)誤差最大為3.31%(算例7)，最大壓應(yīng)變預(yù)測(cè)的相對(duì)誤差最大為8.97%(算例12)，該網(wǎng)絡(luò)預(yù)測(cè)結(jié)果的最大相對(duì)誤差小于10%。因此，可以認(rèn)為網(wǎng)絡(luò)的預(yù)測(cè)效果良好。

在對(duì)以上算例進(jìn)行預(yù)測(cè)時(shí)，分別記錄了有限元計(jì)算和神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)所用的時(shí)間。有限元計(jì)算CPU time為3 387.4 s，而神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)CPU time為0.06 s，瞬間可獲得應(yīng)變結(jié)果。可見(jiàn)，神經(jīng)網(wǎng)絡(luò)在時(shí)間成本上較有優(yōu)勢(shì)，尤其適合可靠性設(shè)計(jì)中的海量計(jì)算。

4　結(jié)論

1)管道以90°穿越角穿越走滑斷層時(shí)主要受拉伸作用，而最大拉、壓應(yīng)變隨斷層位移的增長(zhǎng)并非呈單調(diào)增的趨勢(shì)；當(dāng)斷層位移超過(guò)某一值時(shí)，最大拉應(yīng)變不再增加，而最大壓應(yīng)變隨斷層位移的增長(zhǎng)會(huì)出現(xiàn)極大值。管徑、壁厚的增大以及土彈簧極限抗力的減小更有助于管道抗震，而內(nèi)壓幾乎不影響管道的設(shè)計(jì)應(yīng)變。

2)基于4 817組有限元結(jié)果，創(chuàng)建了用于走滑斷層作用下X80管道設(shè)計(jì)應(yīng)變預(yù)測(cè)的神經(jīng)網(wǎng)絡(luò)模型，驗(yàn)證結(jié)果表明，該模型能準(zhǔn)確預(yù)測(cè)管道的最大拉、壓應(yīng)變，預(yù)測(cè)結(jié)果的最大相對(duì)誤差小于10%。

3)神經(jīng)網(wǎng)絡(luò)的應(yīng)用克服了有限元法計(jì)算時(shí)間長(zhǎng)、硬件設(shè)施高和須要建模經(jīng)驗(yàn)豐富的專(zhuān)業(yè)人員的缺陷，其應(yīng)用方式簡(jiǎn)單，計(jì)算速度快，預(yù)測(cè)精度高，為斷層作用下管道的設(shè)計(jì)應(yīng)變提供較為便捷的預(yù)測(cè)方式，尤其為斷層作用下管道基于應(yīng)變的可靠性分析提供了更加便捷的計(jì)算方式，對(duì)工程應(yīng)用有一定的參考價(jià)值。

[1] 劉嘯奔，陳嚴(yán)飛，張宏，等．跨斷層區(qū)X80鋼管道受壓時(shí)的設(shè)計(jì)應(yīng)變預(yù)測(cè)[J]．天然氣工業(yè)，2014，34(12)：123-130.

LIU Xiaoben, CHEN Yanfei，ZHANG Hong，et al. Prediction on the design strain of the X80 steel pipelines across active faults under stress[J]. Natural Gas Industry, 2014,34(12):123-130.

[2]NEWMARK NM, HALL WJ. Pipeline design to resist large fault displacement[C]// Ann Arbor. Proceedings of the U.S. National Conference On Earthquake Engineering, 1975: 799-807.

[3] KENNEDY R P, DARROW A W, WILLIAMSON R A. Fault movement effects on buried oil pipeline[J]. Transport Engineering Journal, 1977, 103(5): 617-633.

[4]韓銀杉，張宏．走滑斷層作用下管道應(yīng)變解析計(jì)算方法的適用性[J]．油氣儲(chǔ)運(yùn)，2016，35(12)：1329-1336.

HAN Yinshan, ZHANG Hong. Applicability of analytical calculation methods on the pipeline strain under the effect of strike-slip fault[J]. Oil & Gas Storage and Transportation, 2016，35(12):1329-1336.

[5]KARAMITROS D K, BOUCKOVALAS G D, KOURETZIS G P. Stress analysis of buried steel pipelines at strike-slip fault crossings[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(3): 200-211.

[6]劉嘯奔，張宏，李勐，等．?dāng)鄬幼饔孟侣竦毓艿缿?yīng)變分析方法研究進(jìn)展[J]．油氣儲(chǔ)運(yùn)，2016，35(8)：799-807.

LIU Xiaoben, ZHANG Hong, LI Meng, et al. Research progress of strain analysis methods for buried pipelines under faulting process. Oil & Gas Storage and Transportation, 2016, 35(8):799-807.

[7] LIU X B，ZHANG H，HAN Y S，et al. A semi-empirical model for peak strain prediction of buried X80 steel pipelines under compression and bending at strike-slip fault crossings[J]. Journal of Natural Gas Science and Engineering, 2016, 32(32): 465-475.

[8]SHOKOUHI S K, DOLATSHAH A, GHOBAKHLOO E. Seismic strain analysis of buried pipelines in a fault zone using hybrid FEM-ANN approach[J]. Earthquakes and Structures, 2013, 5(4): 417-438.

[9]李劍楠. 基于人工神經(jīng)網(wǎng)絡(luò)模型的埋地管道可靠性研究[D]. 唐山：華北理工大學(xué), 2016.

[10]陶翠翠．改進(jìn)BP神經(jīng)網(wǎng)絡(luò)在埋地金屬管道腐蝕速率預(yù)測(cè)中的應(yīng)用[C]//第七屆沈陽(yáng)科學(xué)學(xué)術(shù)年會(huì)暨渾南高新技術(shù)產(chǎn)業(yè)發(fā)展論壇論文集，沈陽(yáng)，2010：453-458.

[11]馮志剛. 輸油管道的腐蝕檢測(cè)與剩余強(qiáng)度評(píng)價(jià)[D]. 西安：西安石油大學(xué)，2007.

[12] XU Wenzheng, LI Chunbao, CHOUNG J, et al. Corroded pipeline failure analysis using artificial neural network scheme[J]. Advances in Engineering Software, 2017, 112: 255-266.

[13] 王原嵩. 基于GA-BP神經(jīng)網(wǎng)絡(luò)的海底腐蝕管道極限承載力研究[D]. 大連：大連理工大學(xué), 2009.

[14] 汪送，王瑛，李超．BP神經(jīng)網(wǎng)絡(luò)在航空機(jī)務(wù)人員本質(zhì)安全程度評(píng)價(jià)中的應(yīng)用[J]．中國(guó)安全生產(chǎn)科學(xué)技術(shù)，2010，6(6)：35-39.

WANG Song, WANG Ying, LI Chao. Application of BP neural network in inherent safety degree evaluation of aviation maintenance personnel[J]. Journal of Safety Science and Technology, 2010, 6(6):35-39.

[15]王小川，史峰，郁磊，等．MATLAB神經(jīng)網(wǎng)絡(luò)43個(gè)案例分析[M]．北京：北京航空航天大學(xué)出版社，2013.

[16]管志川, 勝亞楠, 許玉強(qiáng),等. 基于PSO優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的鉆井動(dòng)態(tài)風(fēng)險(xiǎn)評(píng)估方法[J]. 中國(guó)安全生產(chǎn)科學(xué)技術(shù),2017, 13(8):5-11.

GUAN Zhichuan, SHENG Yanan, XU Yuqiang, et al. Dynamic risk assessment method of drilling based on PSO optimized BP neural network[J]. Journal of Safety Science and Technology, 2017, 13(8):5-11.

[17]飛思達(dá)科技產(chǎn)品研發(fā)中心. 神經(jīng)網(wǎng)絡(luò)理論與MATLAB7實(shí)現(xiàn)[M]. 北京： 電子工業(yè)出版社, 2005.

[18]趙弘，周瑞祥，林廷圻．基于Levenberg-Marquardt算法的神經(jīng)網(wǎng)絡(luò)監(jiān)督控制[J]．西安交通大學(xué)學(xué)報(bào)，2002，36(5)：523-527.

ZHAO Hong, ZHOU Ruixiang, LIN Tingqi. Neural network supervised control based on Levenberg-Marquardt Algorithm[J]. Journal of Xi’an Jiaotong University, 2002, 36(5):523-527.