局部加權距離度量的雙向稀疏表示目標跟蹤

王業(yè)祥,朱文球,孫文靜

(1.湖南工業(yè)大學 計算機學院,湖南 株洲 412007;2.智能信息感知及處理技術湖南省重點實驗室，湖南 株洲 412007)

0 引 言

目標跟蹤的研究在計算機視覺和模式識別中一直是一個熱點，是各種高級處理如場景理解、行為識別的基礎，在智慧工廠、智能安防系統(tǒng)及智能人機交互等新興產業(yè)中應用廣泛。但是如何提高目標跟蹤在遮擋、形變、光照變化等復雜環(huán)境下的魯棒性一直是一個亟待解決的難點。

近年來，稀疏表示理論[1]已經應用到包括目標跟蹤在內的大量計算機視覺任務中，包括圖像去噪[2]、人臉識別[3]、圖像修復[4]等領域。由于基于稀疏表示的目標觀測模型對環(huán)境的變化具有一定的魯棒性，因此，用稀疏表示解決復雜場景下的目標跟蹤問題具有較大的研究價值。稀疏表示應用于目標跟蹤時，將跟蹤問題的求解轉化為在模板空間中尋求一個稀疏近似解。Zhong等[5]提出將目標模板集和候選模板集進行對比，并把差異度最高的樣本作為目標，但是其用兩個獨立的稀疏表示模型需要對候選樣本集進行兩次稀疏求解，理論難度增大的同時也增加了算法的計算量。Zhuang等[6]用候選樣本集稀疏表示目標正負模板集，構建目標模板和樣本之間的距離概率相似圖，由此確定真實目標。但是該方法必須使用大量的過完備候選樣本集，而且當目標發(fā)生漂移時，不能對正負模板集及時更新，造成概率相似圖不準確以致跟蹤效果下降。

對傳統(tǒng)稀疏表示模型的研究發(fā)現(xiàn)，正向稀疏表示正負目標模板集對候選樣本集的重構，反向稀疏表示候選樣本集對正負目標模板集的重構，基于以上理論首先提出雙向稀疏[7]表示模型框架。該模型以L1范數(shù)[8]來約束正反稀疏表示重構誤差，通過加速逼近梯度(accelerating approximation gradient，APG)算法求得正反稀疏系數(shù)矩陣；在目標模板和候選模板的距離度量上，傳統(tǒng)歐氏距離(Euclidian distance，ED)對光照變化、遮擋比較敏感，從而造成局部權重的不準確性。因此，文中提出改進的局部權重距離度量算法，把最優(yōu)跟蹤目標劃分為16個局部塊，每個局部塊賦一個局部距離權重度量值，根據局部權重度量值更精確地確定候選樣本集與正負目標模板集的相似程度；最后，將該算法與其他算法進行比較。

1 相關內容

1.1 貝葉斯跟蹤框架

(1)

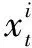
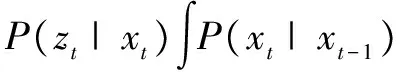
P(xt-1|Zt-1)dxt-1

(2)

P(xt|xt-1)=N(xt;xt-1,σ)

(3)

其中，P(xt|xt-1)是相鄰幀的轉移模型，服從高斯分布。對目標進行仿射變換，即用6個仿射變換參數(shù)來表示目標的狀態(tài)：x={x,y,θ,s,α,φ}，其中x和y分別表示目標水平和垂直方向的平移，θ,s,α,φ分別表示目標狀態(tài)的旋轉角度、尺度變化、比例變化及傾斜角度。P(zt|xt)表示觀測似然模型，可由候選樣本在稀疏映射表對正負模板的區(qū)分度來決定。

1.2 傳統(tǒng)歐氏距離度量

則目標模板t∈Rp×1和候選樣本y∈Rp×1之間的歐氏距離度量可表示為：

(4)

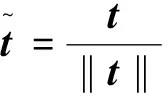
(5)

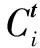
圖1 部分遮擋下傳統(tǒng)歐氏權重分布

2 改進的局部權重距離度量

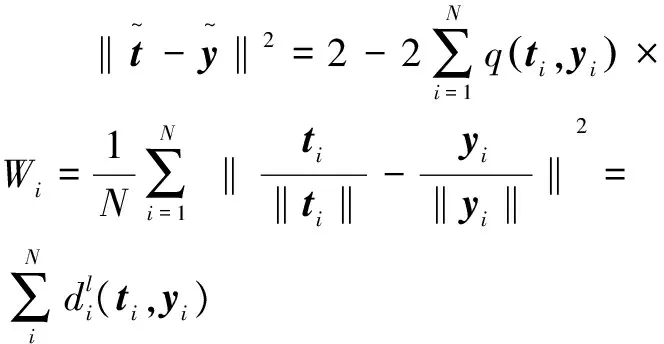
(6)

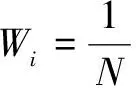
強分類器由五個弱分類器組成，首先獲取上一幀跟蹤目標每個像素的RGB特征值u,u∈R3×1，以及樣本正負標記值(-1和+1)等參數(shù)，然后根據參數(shù)對每個弱分類器進行訓練，每個弱分類器通過權重線性平方回歸來預估計每個像素的正負標記，最后得到一個強分類器F(uj),uj∈R3×1,j=1,2,…,Z。其中j表示跟蹤目標的像素索引，Z表示跟蹤目標像素的總個數(shù)。那么，第t-1幀的整體置信圖sj根據式(7)計算：

sj=1/exp(-Ft(uj)),j=1,2,…,Z

(7)

其中，F(xiàn)t(uj)是第t-1幀，負樣本區(qū)域為0，正樣本區(qū)域為(0,1]。

得到第t-1幀的整體置信圖后，就容易得到第t幀跟蹤目標局部塊的相似性局部距離權重Wi。

(8)

其中，∑sj表示屬于第i個局部塊的權重。

由置信圖分配的局部權重距離在遮擋的區(qū)域分配較小的權重，在目標區(qū)域則分配較大的權重。后續(xù)幀目標跟蹤的局部權重距離dl(t,y)為：

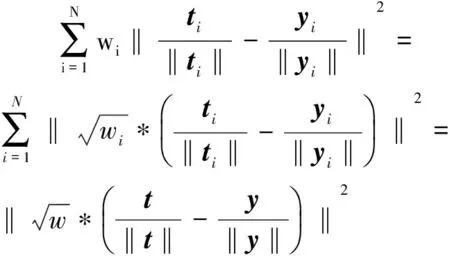
(9)

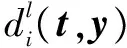
(10)

式(10)說明改進的局部權重距離度量具有約束性。

當然，為了適應目標外觀變化的隨機性難題，就必須解決分類器的更新問題。文中的分類器更新策略如下：

(11)

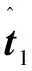
3 雙向稀疏表示

3.1 模型建立

目標模板集由m個正模板和n個負模板組成：T={tj∈Rp×1},j=1,2,…,q，m+n=q。文中用RGB顏色特征來跟蹤目標，p是每一個模板的特征維度。那么目標模板集可表示為：

(12)

傳統(tǒng)正向稀疏表示是目標模板集T對候選模板集y的稀疏表示：

(13)

其中，αi為第i個樣本的稀疏表示向量且αi∈Rq×1，α∈Rq×r；yi為第i個候選樣本；r為候選樣本集個數(shù)；λ1為懲罰項。可根據αi求得觀測似然函數(shù)并求出yi的接受概率；同理，逆稀疏表示模型是候選樣本集y對目標模板集T的稀疏表示：

(14)

其中，βj為第j個目標模板的稀疏表示向量且βj∈Rr×1，β∈Rr×q；Tj為第j個目標模板；q為目標模板集個數(shù)；λ2為懲罰項。可根據βj求得觀測似然函數(shù)并求出Tj的接受概率。

正反向稀疏表示都需要計算各自稀疏表示稀疏矩陣，雖然分別基于正反向稀疏表示的跟蹤框架也取得了比較好的跟蹤效果，但是它們的稀疏系數(shù)矩陣是通過幾次迭代收斂得到的，與最優(yōu)目標仍有一定的誤差。

通過對比研究發(fā)現(xiàn)，樣本集合y與目標模板集合T之間的相關性是一個固有屬性，那么稀疏系數(shù)矩陣α和β之間的相關性也是一個固有屬性，即矩陣α和β之間具有某種相似性，文中添加如下限制性條件：

‖α-βΤ‖2≤η,s.t.α≥0,β≥0

(15)

基于這一條件，構造雙向稀疏表示目標跟蹤框架：

β‖2+λ1‖α‖1+λ2‖β‖1}

(16)

其中，ψ是懲罰項。

基于雙向稀疏框架完全考慮了正反稀疏系數(shù)矩陣之間的相關性，實驗證明雙向稀疏比單向稀疏表示能更好地跟蹤目標。

對于求解正向稀疏表示系數(shù)矩陣α和逆向稀疏系數(shù)矩陣β的問題，文中采用APG[10]快速算法框架。

3.2 觀測似然值的求解

文中用正負目標模板的差異度進行觀測似然函數(shù)的求解，稀疏系數(shù)矩陣α的每一列可作為候選樣本在目標模板上的區(qū)分度，同理，稀疏矩陣β的每一行亦可。與其他傳統(tǒng)目標跟蹤算法一樣，為了得到更好的區(qū)分度，使用式(9)改進的局部權重距離計算目標模板集與候選樣本集之間的局部權重距離，得到q×r個權重集合：

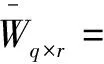
i=1,2,…,q,j=1,2,…,r,z=1,2,…,N

(17)

(18)

當然，每個稀疏映射表可化簡為：

(19)

考慮到負模板個數(shù)較多，使用池化方法簡化對稀疏映射表的運算：

(20)

其中，L(f,l)是取f這個函數(shù)中第l大的數(shù)，文中l(wèi)值取正模板個數(shù)的一半；Si-pos與Si-neg分別表示第i個候選模板與前l(fā)個正負模板之間的關系。

(21)

(22)

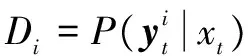
3.3 模板在線更新

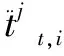
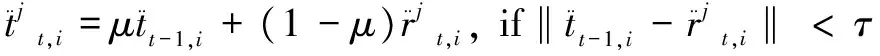
j=1,2,…,mi=1,2,…,N

(23)

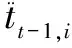
對于負模板的更新，文中用與目標相差甚大的候選模板更新為負模板。在當前幀結束時，利用上一幀跟蹤目標的中心點坐標來確定候選模板集，并以此候選模板集來替代更新負模板集。

4 實驗結果及分析

文中算法用Matlab編寫。相關參數(shù)如下：分類器更新常數(shù)ψ=0.2,正向模板更新常數(shù)τ=0.1，正模板、負模板以及候選模板個數(shù)分別為10、100和500，每個模板圖像大小為32×32像素，分為16個8×8像素的局部塊。為了驗證該算法的性能，現(xiàn)與增量視頻跟蹤[11](IVT)、加速逼近梯度跟蹤[12](APGL1)、分解視頻跟蹤[13](VTD)、多實例學習[14](MIL)、基于片段的跟蹤[15](frag)五種經典方法進行性能對比，實驗所用視頻也均為挑戰(zhàn)性的經典序列。

4.1 定性分析

如圖2所示，在Deer視頻序列中，剛開始Frag和L1開始出現(xiàn)漂移，在第18幀時，MIL也開始出現(xiàn)跟蹤目標丟失，只有VTD和文中算法跟蹤效果較好。Singer序列第107幀時受強烈的光照影響，只有IVT、VTD和文中算法跟蹤比較穩(wěn)定，隨后隨著目標的縮小，只有文中算法準確跟蹤到目標。在Face中，當目標受到嚴重遮擋時，MIL算法首先跟蹤失敗，其他算法良好。從圖中可以看出，文中算法一直準確跟蹤到目標，其余算法在不同的視頻系列中效果差強人意，產生明顯的漂移甚至跟蹤失敗，因此文中算法優(yōu)于其他五種算法。

4.2 定量分析

文中應用中心位置誤差和重疊率來衡量各種算法的性能。平均中心位置誤差越小，跟蹤效果越好，反之越差。從表1可看出，文中算法在不同視頻序列中，其中心位置誤差均最小，性能最優(yōu)。

圖2 跟蹤結果對比

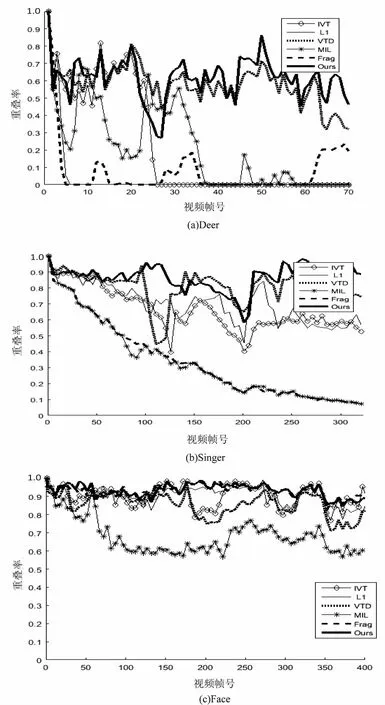
圖3 重疊率對比

表1 中心位置誤差對比

5 結束語

文中提出了一種基于雙向稀疏表示及改進的權重度量算法，利用過完備字典和候選目標來互相表示，通過正負稀疏矩陣計算候選目標的正負相異度作為觀測似然值；在模板度量上采用改進的歐氏距離權重度量方法，采用分類器權重迭代及分塊思想解決傳統(tǒng)相似性度量問題。實驗結果證明了文中算法具有較好的跟蹤性能。但是算法在目標瞬間劇烈抖動時跟蹤性能一般，下一步重點解決此問題，以提高算法的適應性。

參考文獻:

[1] 孫君頂，趙慧慧.圖像稀疏表示及其在圖像處理中的應用[J].紅外技術,2014，36(7):533-537.

[2] 孫玉寶,韋志輝,吳 敏,等.稀疏性正則化的圖像泊松去噪算法[J].電子學報,2011,39(2):285-290.

[3] 謝文浩,翟素蘭.基于加權稀疏近鄰表示的人臉識別[J].計算機技術與發(fā)展,2016,26(2):22-25.

[4] 李志丹,和紅杰,尹忠科,等.結合顏色和梯度信息的稀疏圖像修復算法[J].計算機研究與發(fā)展,2014,51(9):2081-2093.

[5] ZHONG W.Robust object tracking via sparsity-based collaborative model[C]//Proceedings of the 2012 IEEE conference on computer vision and pattern recognition.Washington DC,USA:IEEE Computer Society,2012:1838-1845.

[6] ZHUANG B,LU H,XIAO Z,et al.Visual tracking via discriminative sparse similarity map[J].IEEE Transactions on Image Processing,2014,23(4):1872-1881.

[7] 王 華,王 倩,顧 鑫,等.基于雙向稀疏光流融合的小目標檢測方法[J].電視技術,2016,40(3):122-125.

[8] MEI X,LING H.Robust visual tracking using l1 minimization[C]//IEEE international conference on computer vision.[s.l.]:IEEE,2009:1436-1443.

[9] 徐 濤,曾 濤，崔智社.基于貝葉斯推理的目標跟蹤[J].計算機仿真,2004,21(5):74-77.

[10] CHEN X,PAN W,KWORK I T, et al. Accelerated gradient

method for multi-task sparse learning problem[C]//Proceedings of the 2009 ninth IEEE international conference on data mining.Washington DC,USA:IEEE Computer Society,2009:746-751.

[11] ROSS D A,LIM J,LIN R S,et al.Incremental learning for robust visual tracking[J].International Journal of Computer Vision,2008,77(1-3):125-141.

[12] BAO C,WU Y,LING H.Real time robust L1 tracker using accelerated proximal gradient approach[C]//IEEE conference on computer vision & pattern recognition.Washington DC,USA:IEEE Computer Society,2012:1830-1837.

[13] KWON J,LEE K M.Visual tracking decomposition[C]//IEEE conference on computer vision and pattern recognition.Washington DC,USA:IEEE Computer Society,2010:1269-1279.

[14] BABENKO B,YANG M,BELONGIE S.Visual tracking with online multiple instance learning[C]//IEEE conference on pattern analysis and machine intelligence.Washington DC,USA:IEEE Computer Society,2009:983-990.

[15] ADAM A,RIVLIN E,SHIMSHONI I.Robust fragments-based tracking using the integral histogram[C]//IEEE conference on computer vision and pattern recognition.Washington DC,USA:IEEE Computer Society,2006:798-805.