BP神經網絡隱含層節點數確定方法研究

王嶸冰，徐紅艷，李 波，馮 勇

(遼寧大學 信息學院，遼寧 沈陽 110036)

0 引 言

人工神經網絡具有自學習、自組織和優良的非線性逼近能力，因此眾多領域的學者都在對其進行研究和應用。在實際應用中，其中一種人工神經網絡—BP神經網絡(back propagation neural networks，BPNN)最為人們熟知，并廣泛應用于人工智能、圖像處理、優化算法、數據挖掘等重要領域。

在對BPNN進行深入研究的過程中，學者們提出了一個非常重要的、不可忽略的問題，即BPNN隱含層節點數確定問題。由于對神經網絡隱含層節點數的確定缺乏有效的方法，目前僅能憑經驗和不斷地實驗來確定隱含層節點數。針對這個問題，文中提出了一種行之有效的算法，即“三分法”算法。該算法可以簡單、快速地確定BPNN隱含層節點數。

1 相關研究

1.1 BPNN

1986年，Rumelhart等提出了誤差反向傳播法，即BP算法[1]。BPNN能夠實現M-N維的映射關系，而無需事先知道映射關系的數學方程式。BPNN模型由三部分構成：輸入層、隱含層以及輸出層[2]，模型圖如圖1所示。

圖1為三層前饋神經網絡，不含Input層，整個網絡含有兩個隱含層Hidden1和Hidden2，一個輸出層Output，各層之間是全連接的關系。

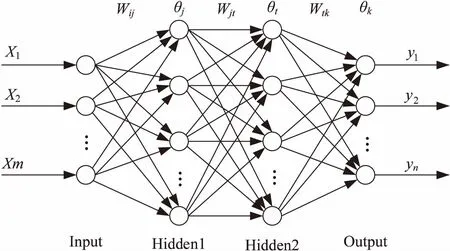
圖1 三層BPNN

BPNN實現了M維到N維的一個非線性映射關系，它包括兩個過程，一是前向傳播過程，二是誤差反向傳播過程。

當一個模式從輸入端輸入網絡之后，這個模式將在BPNN中流動，模式通過權值線路進入每一個隱含層神經元節點，利用激活函數，隱含層各個神經元對其進行加權求和處理，之后經過隱含層和輸出層之間的權值線路進入輸出層單元，處理后在輸出層產生一個輸出模式。在輸入模式轉換成輸出模式的期間，從輸入層到輸出層逐步更新各層狀態的過程即前向傳播過程。接著計算輸出模式和期望模式的誤差，如果誤差大于設定的精度閾值，將誤差順著來路逐層進行反向傳播，接著更新網絡權值。迭代前向傳播和誤差反向傳播這兩個過程，直至所有訓練樣本的誤差平方和都滿足精度要求為止，至此BPNN的整個學習過程就完成了。

1.2 影響BPNN性能的參數

為了設計合理的BPNN，有必要探討影響BPNN性能的參數，影響BPNN性能的參數如下：

(1)隱含層數：隱含層數的增加可以降低網絡誤差，提高精度，但同時也會使網絡復雜性增大，導致網絡的訓練時間被增大和出現“過擬合”傾向的可能性也被增大。

(2)隱含層節點數：在BPNN中，隱含層節點數是一個非常重要的參數，它的設置對BPNN的性能影響很大，而且是“過擬合”現象的直接原因。但遺憾的是，目前理論上還不存在一種科學普遍的確定方法。這個問題將是文中關注的重點。

(3)網絡的初始連接權值：BP算法的先天設計不可避免地使誤差函數會有多個局部極小點存在，網絡初始連接權值不同，可能導致BP算法收斂的結果不同，而這個結果不能確定是全局最優解，有可能是局部最優。

(4)學習率：網絡訓練時，網絡學習的穩定性受到學習率的影響。設定的學習率大，網絡學習速度快，但會導致修正權值時權值會呈現不規則跳躍而無法收斂；設定的學習率小，網絡學習速度慢，可能使網絡收斂于某個極小值，缺點是會導致學習時間過長。

(5)動量系數：為解決易收斂到極小值、訓練時間長等缺陷，引入了動量系數因子[3]。附加動量項能夠使得權值的調整趨于平滑穩定，易找到全局最小值[4]。

2 BPNN與隱含層節點數

2.1 隱含層節點數對BPNN的影響

在BPNN中，隱含層節點數是一個非常重要的參數，它的設置對BPNN的性能影響很大[5]，而且是“過擬合”現象的直接原因，目前理論上還沒有一種科學的方法可以確定隱含層節點數。由于輸入輸出層節點數，以及問題的復雜度和轉換函數等都可能影響隱含層節點數的確定，它的確定有了更多的不確定性。

若隱含層節點數太少，那么會使得網絡無法學習；若太多，雖然在一定程度上可以減小系統誤差，但無疑會增加網絡學習的時間，而且會使訓練掉入局部極小點的陷阱，這也是“過擬合”的內在原因。因此，如何合理設計隱含層節點數，是一個不可避免的問題。確定隱含層節點數可以遵循一條基本原則，盡可能取較少的節點數來滿足問題的精度要求。

對非訓練樣本的支持能力稱為網絡泛化能力[6]。而泛化能力與網絡的結構，即隱含層數和隱含層節點數有關[7]。學者Nielson通過理論證明存在一個BPNN，只有一個隱含層，但能夠逼近在閉區間連續的任何函數[8]，因此不用考慮隱含層層數問題。

2.2 傳統隱含層節點數的確定方法

隱含層節點數的選擇是個十分復雜的問題，需要設計者有著長期的實踐積累，憑借自己以往的經驗以及借助多次實驗進行確定。隱含層節點數與問題的需求、輸入輸出單元的數目有著不可割舍的直接關系。若數目太少，則BPNN不能獲取足夠的信息用來解決問題需求；若數目太多，會增加學習時間，還會使學習時間過長，卻不能保證最終結果最好，同時可能出現“過擬合”問題。文獻[9]說明最佳的隱層節點數一定存在，如何尋找得到這個最佳節點數是一個值得思考的問題。針對該問題，許多學者給出了各種解決方案[10-13]，也提出了不少經驗公式。

(1)

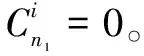
n1=(n+m)1/2+a

(2)

其中，n為輸入層節點數；m為輸出層節點數；a為1～10之間的常數。

n1=log2n

(3)

解決方案總結起來有以下幾類：

(1)實驗法，這是一種最無奈的方法，而且消耗大量的人力；

(2)將解空間限制到某個區間內，在這個解空間中進行暴力破解，雖然簡單，但消耗時間；

(3)引入超平面、動態全參數自調整等概念，這些都使得算法過于復雜，甚至超過了BPNN學習算法的復雜度，運行這些算法需要消耗過長的時間，所以需要思考一種簡單有效的算法。

通過聯立式1～3并求解，可以得到一個關于隱含層節點數的區間[a,b]。這個區間意味著最佳隱含層節點數所在的一個區間，只要在這個區間中尋找，就可以找到它。

第一種方法，最簡單也是最容易想到的，即可以使用暴力破解的思想。所謂的暴力破解法，就是利用整個解空間中的每一個解進行驗證計算。

將[a,b]之內的所有可能解代入BPNN，然后每一個解構成一個BPNN，將所有的樣本通過這些神經網絡進行訓練，從而得到這些BPNN中最小的誤差值，所對應的隱含層節點數即為所求[14]。

暴力破解法由于搜索了整個解空間，因此該算法一定是有效的，但對于時間復雜度而言，當這個區間很小或者測試樣本量很小時，暴力破解算法的時間是可以接受的，但當這個區間特別大或者測試樣本量很大時，所耗費的時間就可能無法容忍，需要繼續改進。

暴力破解法時間消耗過長主要是因為搜索了整個解空間，如果能夠在求解的過程中縮小解空間，那么時間消耗就可以減少，從而優化暴力破解算法。

3 改進的隱含層節點數確定方法

3.1 “三分法”算法思想

二分法查找是在一個有序的數組中進行折半查找，從而將查找算法的時間復雜度降到了O(log2n)。文中借鑒了二分法查找算法思想，但是考慮由于隱含層節點數和誤差的關系的特殊性，不能照搬二分法，需要設計為三分法。

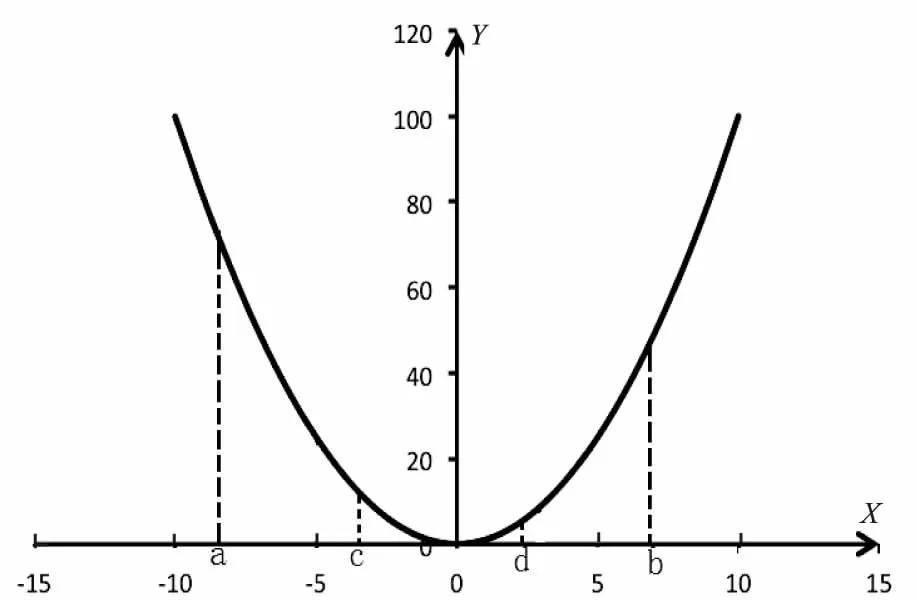
圖2 拋物線曲線

該算法可以一次性去除2/3的不符合選項。如圖2所示的拋物線中，只利用函數值如何查找最低點的位置。

第一種方法可以使用暴力破解。

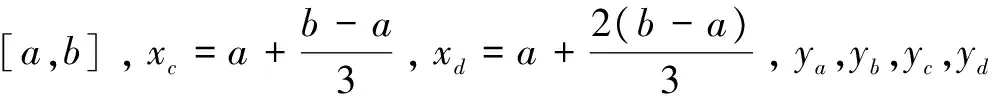
(4)

當最低點位于區間內時，那么最低點所在的區間的斜率絕對值最小(圖2中為區間[c,d])，且左邊區間的斜率為負，右邊的區間為正。所以要找到最小點，只需從[c,d]之間查找。然后在[c,d]中迭代使用“三分法”，直到[a,b]區間長度小于等于4(不能構成三個斜率)，此時只需依次比較這四個節點就可以找到最低點。

通過上述可知，三分法的適用范圍為區間存在最優解，且誤差模型近似為拋物線。通過式1～3獲得區間內一定包含了最優的隱含層節點數，并且也可知它符合拋物線模型。

研究區間很大時，如果忽略一些特殊點形成的“突刺”(一些特殊的點上誤差可能會高于理想的誤差而出現波動，即突刺)，那么誤差的模型是一個拋物線模型。拋物線模型最低谷是誤差最小點，也就是最佳的隱含層節點數；從這個點往兩側延伸，隨著遠離這個平衡點，那么誤差會逐漸增大。當隱含層節點數為1時，可以認為這個網絡是無用的；當隱含層節點數是一個正的無窮時，網絡中的冗余知識使得網絡也是不可用的。

至此，可知“三分法”的實質就是將區間[a,b]分成三段，然后研究這三段的變化趨勢，從而預測最優的隱含層節點數存在于哪個區間之內。斜率代表了曲線的變化趨勢，斜率越小，說明變化趨勢越小，也就說明了隱含層節點數就隱藏在這里。

3.2 算法合理性驗證

為了說明算法的合理性，并且為了演示算法的運行步驟，在此先簡要利用其他研究者的實驗成果進行簡單驗證，后面會繼續利用實驗驗證“三分法”算法的合理性。

在文獻[15]中，有一章節研究了隱含層節點數和誤差的關系，這篇論文是關于BPNN對產品質量合格率預測的研究，其實驗結果如圖3所示。

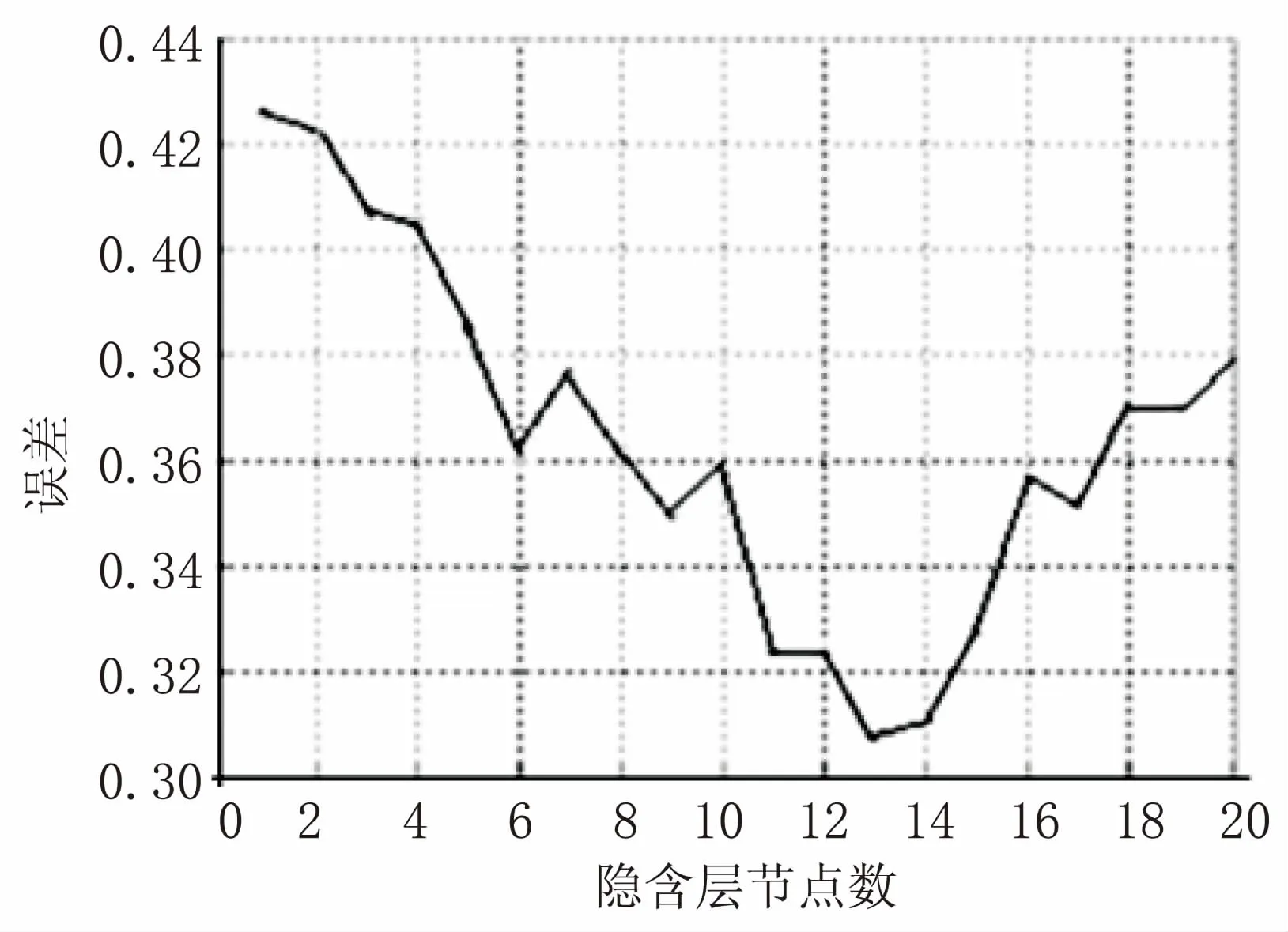
圖3 隱含層和誤差的關系曲線

通過觀察圖3可知，這是一個不規則的拋物線模型，某些地方呈不規則無規律變化，而在整體變化趨勢上卻呈拋物線變化，支持了上文的研究理論。對于這個關系圖，如果使用暴力破解，即依次驗證1～20個節點，那么需要訓練20次，才能確定節點數最優解為13；如果使用三分法，那么很快就確定到節點數為6～13個。

接下來，探討BP網絡隱含層節點數確定步驟。設ki,j表示區間(i,j)的斜率，比如k1,6表示區間(1,6)的斜率。

第一步：因為k1,6<0&&k13,20>0,說明在區間(1,6)誤差在下降，在區間(13,20)誤差在上升，那么說明最優解可能在區間(7,12)，所以可取區間(7,12)，繼續使用三分法。

第二步：因為k7,8<0&&k9,10<0&&k11,12<0，說明誤差一直在下降，則可選取區間(11,12)，如此再比較隱含層節點數11和隱含層節點數12。

第三步：檢測所求解的兩側的兩個點就可以定位到13。

如此只需訓練11次就可找到最優解，比正常的快了幾乎一倍。接下來，仔細分析“三分法”算法思想。

實際上三個區間的方向性共有8種變化。設三個區間的斜率分別為k1,k2,k3，則這三個斜率的變化趨勢可以分為6種情況。

(1)k1<0&&k2>0&&k3<0。

k1<0說明誤差在下降，k2>0說明誤差在上升，k3<0說明誤差在下降，出現這種現象可以認為誤差出現了“跳躍”，因此不能使用“三分法”，而使用普通的暴力破解法效果會更好。

(2)k1<0&&k2>0&&k3>0。

k1<0說明誤差在下降，k2>0說明誤差在上升，k3>0說明誤差在上升，所以可以確定最優解在中間段區間，即使在第一段區間的末尾，由于算法會加一個調節因子，依然可以找到。

(3)k1<0&&k2<0&&k3>0。

該情形與情形(2)類似。誤差變化是第一段區間下降，第二段區間下降，第三段區間上升，所以依然選擇中間段區間。

(4)k1<0&&k2<0&&k3<0。

三者全都小于0，說明誤差一直在下降，所以選擇第三段區間。

(5)k1>0&&k2>0&&k3>0。

三者均大于0，說明誤差一直在上升，所以選擇第一段區間。

(6)其他情況，可以認為區間震蕩，無法確定最優解會出現在哪個區間，需要使用暴力破解法。

由于算法利用的是區間的變化趨勢，所以每一段區間最少為三個點，三個區間則最少需要七個點。因此設置7為臨界值，當區間大小大于等于7時，一律使用暴力破解法。

其次，對于每一種情況，最優解有可能在某個區間的端點出現，這樣的話有可能會錯過這個解，因此為了防止最優解在區間端點出現，加入調節因子m,n。

3.3 “三分法”算法描述

在前面詳細論述了“三分法”算法的求解原理和算法思想，該算法有效且簡單。引入BPNN中，首先構建BPNN，利用求得的節點數區間，代入隱含層構建對應的BPNN，BPNN構建完成后，將訓練樣本依次通過BPNN進行訓練，利用測試樣本測試網絡，這樣最終會得到BPNN的誤差和隱含層節點數的關系。

“三分法”算法流程：

(1)根據經驗公式1～3確定a,b；

(2)如果b-a小于7，跳轉到(8)，否則繼續執行；

(3)計算c,d，并獲取ka,c,kc,d,kd,b；

(4)如果ka,c<0&&kc,d<0&&kd,b<0，則a=b，跳轉到(2)；否則繼續向下執行；

(5)如果ka,c>0&&kc,d>0&&kd,b>0，則b=c，跳轉到(2)；否則繼續向下執行；

(6)如果ka,c<0&&kc,d>0&&kd,b>0，則a=c,b=d，跳轉到(2)；否則繼續向下執行；

(7)如果ka,c<0&&kc,d<0&&kd,b>0，則a=c,b=d，跳轉到(2)；否則跳轉到(8)；

(8)添加調節因子a=a-m，b=b+n，若a小于等于0，重置為1；

(9)暴力求解。

4 實驗結果與分析

4.1 實驗環境

文中采用Java編程技術，使用的開發工具包是jdk1.7，集成開發環境采用Eclipse，它可以很好地支持Java應用程序編程。Matlab是一種很強大的工具，集成了計算、可視化和程序設計等功能，有多種工具箱，其中包括神經網絡工具箱。神經網絡工具箱包括不同神經網絡模型的網絡學習和訓練函數，其中就有BPNN，包括BPNN的新建、訓練、測試，為BPNN的仿真實驗提供了便利。

4.2 隱含層節點數確定實驗

為了驗證“三分法”算法的正確性，需要進行兩部分實驗。首先需要驗證BPNN誤差和隱含層節點數的關系，其次需要進行“三分法”算法的驗證。

實驗采用UCI上的數據集Wine-data，對三個不同品種的葡萄酒分別進行化學分析，從中分析出主要成分并記錄該值。該數據集的任務就是實現數據分類，從而區分其所屬品種。

實驗獲取到的結果如圖4所示。

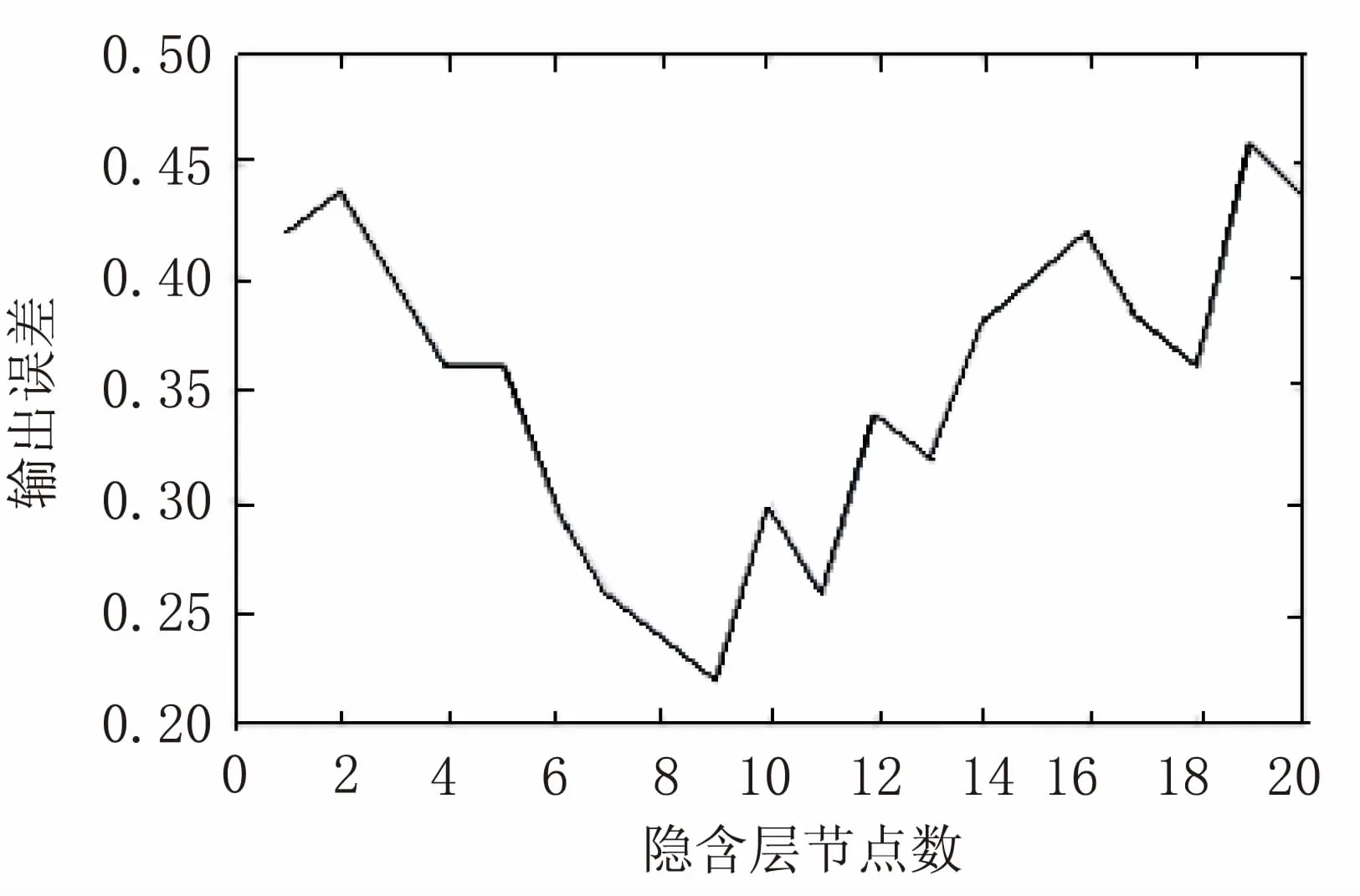
圖4 網絡誤差與隱含層節點數的關系

通過對Wine-data數據集的實驗，發現隱含層節點數與誤差的關系基本符合拋物線的形式，證明了“三分法”算法的基礎是有效的。而通過對這組實驗結果使用“三分法”算法，最終可以獲取到最佳解。程序運行過程中a，b，c，d(m,n均設置為0)變化是：

(1)a=1，c=7，d=13，b=20；

(2)a=7，c=9，d=11，b=13；

(3)a=9，b=11。

傳統確定隱含層節點數的方法，需要實驗節點數為1～20共20次的實驗，而新的“三分法”算法實驗只需要進行1，7，9，10，11，13，20共7次實驗，速度提高了1.8倍，證明了“三分法”算法相對于傳統方法有了明顯的改進。

5 結束語

針對BPNN結構難以確定的問題，提出了“三分法”算法。通過參考相關文獻、研究已有成果，發現BPNN的誤差和隱含層節點數的關系基本符合拋物線模型，所以可以通過研究誤差的趨勢，很快定位到最優解的位置，這是“三分法”算法的基礎。同時，為了解決不符合拋物線模型的情況，增強“三分法”算法的魯棒性，結合了暴力破解法。通過示例演算可知，“三分法”算法可以快速、有效地確定隱含層節點數，是一種行之有效的算法。

參考文獻：

[1] RUMELHART D E.Learning representation by back-propagating errors[J].Nature,1986,323(6088):533-536.

[2] 周啟超.BP算法改進及在軟件成本估算中的應用[J].計算機技術與發展,2016,26(2):195-198.

[3] 師 黎,陳鐵軍.智能控制理論及應用[M].北京:清華大學出版社,2009:104-105.

[4] 王晶晶,王 劍.一種BP神經網絡改進算法研究[J].軟件導刊,2015,14(3):52-53.

[5] BAHADIR E.Prediction of prospective mathematics teachers' academic success in entering graduate education by using back-propagation neural network[J].Journal of Education and Training Studies,2016,4(5):113-122.

[6] 周冬冬.BP神經網絡樣本數據預處理應用研究[D].重慶:重慶大學,2011.

[7] 李武林,郝玉潔.BP網絡隱節點數與計算復雜度的關系[J].成都信息工程學院學報,2006,21(1):70-73.

[8] AZGHADI S M R,BONYADI M R,SHAHHOSSEINI H.Gender classification based on feed forward back propagation neural network[C]//International conference on artificial intelligence & innovations:from theory to applications.[s.l.]:[s.n.],2007:299-304.

[9] RASTEGAR R,HARIRI A.A step forward in studying the compact genetic algorithm[J].Evolutionary Computation,2006,14(3):277-289.

[10] 沈花玉,王兆霞,高成耀,等.BP神經網絡隱含層單元數的確定[J].天津理工大學學報,2008,24(5):13-15.

[11] 張德賢.前向神經網絡合理隱含層結點個數估計[J].計算機工程與應用,2003,39(5):21-23.

[12] 夏克文,李昌彪,沈鈞毅.前向神經網絡隱含層節點數的一種優化算法[J].計算機科學,2005,32(10):143-145.

[13] 田國鈺,黃海洋.神經網絡中隱含層的確定[J].信息技術,2010(10):79-81.

[14] KHANLOU H M,SADOLLAH A,ANG B C,et al.Prediction and optimization of electrospinning parameters for polymethyl methacrylate nanofiber fabrication using response surface methodology and artificial neural networks[J].Neural Computing and Applications,2014,25:767-777.

[15] 溫 文.基于改進BP神經網絡的產品質量合格率預測研究[D].廣州:華南理工大學,2014.