基于Greenplum數據庫的查詢優化

鄒承明，謝　義，吳　佩

(1.交通物聯網技術湖北省重點實驗室(武漢理工大學)，武漢 430070；　2.武漢理工大學 計算機科學與技術學院，武漢 430070)(*通信作者電子郵箱17607197069@163.com)

0　引言

在如今大數據時代的背景下，為了滿足大規模數據處理及分析的需求，分布式數據庫應運而生，并逐漸取代集中式數據庫成為當今主流的數據分析系統。但同時，大規模數據的增長降低了分布式數據庫的查詢效率，如何提升查詢效率是分布式數據庫領域中的熱點和難點。近年來，有不少學者進行了尋求查詢優化方案的研究，其中，對數據庫系統架構和數據處理方式的創新是優化分布式數據庫的重要途徑。無共享架構(Shared-nothing architecture)[1]是在分布式數據庫優化過程中產生的一種集群架構。BigTable[2]、Google File System[3]、MapReduce[4]等都是典型的大規模并行處理(Massive Parallel Processing, MPP)架構，它們的成功推動了無共享架構集群的發展。Greenplum[5]是目前最先進的分布式開源數據庫技術之一，其高度并行性的優勢將推動并促進基于MPP架構的分布式數據庫的發展與流行[6]。

查詢操作是分布式數據庫對用戶提供的最基本服務。本文將從最優查詢計劃生成方法的角度來對Greenplum數據庫的查詢操作進行優化。最優查詢計劃的生成問題是一個最優解的求解問題。對于最優解的求解，有兩種典型的方法：基于啟發式的方法和隨機搜索方法。動態規劃是典型的基于啟發式的方法。文獻[7-8]都利用動態規劃解決優化問題，并將其應用到查詢優化中，這種方法雖然能得到最優解，但隨著連接關系數的不斷增大，搜索效率會變得非常低，因此動態規劃算法不太適合大規模數據場景下復雜的多表連接查詢的優化問題。遺傳算法作為一種有效的隨機搜索算法，隨著問題規模的增大，其優勢會比較明顯[9]。文獻[10]將遺傳算法應用于分布式數據庫查詢計劃生成，與動態規劃相比，這種方法的搜索效率更高，但是該方法不一定能保證獲得最優解，而且該方法的好壞依賴于種群的初始化、變異交叉操作的選擇以及適應度函數的選擇。蟻群算法也是一種有效的隨機搜索算法。文獻[11]提出了一種基于蟻群算法的方法來減少查詢過程中連接操作產生的代價，從而獲得一個關系數據庫復雜查詢的最優查詢計劃；但是該方法的代價模型中只考慮了連接操作產生的代價，忽略了分布式數據庫節點之間的數據傳輸代價。文獻[12]提出了最大最小蟻群算法，這種改進的蟻群算法進一步解決了算法過早收斂的問題，求解效率更高。經過對上述文獻中算法的對比，本文基于文獻[12]的算法提出了一種并行最大最小蟻群算法來搜索最優連接順序。

基于以上研究，為了提升Greenplum數據庫的查詢效率，本文提出了一種有效的基于代價的最優查詢計劃生成方法，并通過實驗驗證了其有效性。

1　代價模型

基于代價的查詢優化是MPP數據庫的核心技術。Greenplum數據庫的查詢優化器就是以代價作為目標，搜索具有最小代價的查詢計劃[13]。這種基于代價的查詢優化首先根據一個查詢語句的邏輯生成樹，預估每個查詢策略的代價，然后從中選擇代價最小的路徑作為最終的物理執行計劃。因此，代價預估是基于代價的查詢優化中的一個重要問題。本文通過對分布式數據庫查詢代價的組成進行分析，設計了一個有效的查詢代價模型。通過這個代價模型，在任務實際執行之前，能夠預估整個任務完成的總代價。

一般情況下，集中式數據庫系統的總查詢代價公式為：Ctotal=CCPU+CI/O，其中CCPU表示CPU代價，CI/O表示I/O代價。但是，分布式數據庫是由節點之間互相協作完成整個查詢任務，節點之間的交互同時會產生通信代價Ctrans，所以，分布式數據庫的總查詢代價公式可表示為：Ctotal=CCPU+CI/O+Ctrans。通信代價的估算可以通過式(1)來實現，其中X表示需要傳輸的數據量，C0和C1是兩個常量系數。

Ctrans(X)=C0+C1*X

(1)

1.1　相關參數

分布式數據庫系統中一般都會存儲著數據表的統計信息，這些統計信息可以用來對代價進行估計。這類信息通常存儲在數據庫的數據字典中，供查詢優化器使用[6]。從Greenplum數據庫的數據字典中可以獲得代價估計所需的統計信息。Greenplum數據庫對代價的估計忽略了數據傳輸的代價，因此，本文將數據傳輸的代價考慮進來，提出了一種新的代價模型。該模型需要從數據字典中獲取的參數主要是|R|和V(a,R)。其中:|R|表示關系R中的元組數，V(a,R)表示關系R中的屬性a所具有的不同值的數目。

1.2　代價估算

假設給定一個連接S=R1joinR2，R1和R2是兩個要連接的關系表。從數據傳輸代價Costtrans(S)和連接產生的數據量Costjoin(S)兩個方面來對該連接進行代價估算，如式(2)所示：

Costtotal(S)=Costtrans(S)+Costjoin(S)

(2)

1)數據傳輸代價：影響數據傳輸代價的最主要因素是進行連接的關系表的規模大小。但是，在網絡傳輸速度很快的情況下，數據傳輸的代價相對CPU對數據進行處理的代價影響較小。為了統一計算連接的代價，本文為數據傳輸代價設置一個權值ω，數據傳輸代價如式(3)所示：

Costtrans(S)=ω*(|R1|+|R2|)

(3)

2)連接產生的數據量：某一個連接產生的數據量越大，那么該連接產生的代價就越大，針對該連接的下一個連接的代價也就更大。因此，本文將連接產生的數據量作為連接的代價。對于連接S=R1joinR2，連接中屬性所具有的不同值的數目可通過式(4)計算：

(4)

設Attr為關系表R1和R2的公共屬性集合，連接產生的數據量可以用式(5)來表示：

(5)

在分布式數據庫中，一個多表連接查詢語句的查詢執行計劃都是用一棵連接樹來表示的。假設用連接樹的內節點Si(i=1,2,…,n-1)來表示中間連接關系，那么該連接樹內所有內節點S的代價總和就可以表示某一個查詢計劃的總代價。可以用式(6)來表示一個多表連接查詢執行計劃的代價模型：

(6)

2　并行最大最小蟻群算法

Greenplum數據庫中的復雜查詢基本上都會涉及到跨表查詢。跨表查詢的一個最基本操作就是連接，而連接操作也是分布式數據庫中一個關鍵的操作。在連接操作中，內連接滿足交換律，而外連接和子查詢都可通過一定方式轉換為內連接[14]。通常情況下，兩個關系表之間的連接操作是最耗時的操作之一[15]，因此，涉及到連接操作的處理代價是影響復雜查詢語句代價的主要因素，這種連接代價主要取決于給定的查詢語句中所涉及到的關系表的連接順序。假設數據庫中有三個關系表R1、R2和R3，這三個表所有可能的連接順序有：(R1R2)R3，R1(R2R3)和(R1R3)R2。不同的連接順序會產生不同的查詢計劃代價，搜索最優的連接順序對提升查詢效率起著重要作用，因此，對連接順序進行優化是分布式數據庫多表連接查詢的一個研究重點。一般情況下，影響連接順序優化的因素有以下三個：搜索空間、代價模型和搜索策略。本文在進行連接順序優化過程中，采用第1章中設計的代價模型；對于搜索策略，本文實現了一種并行化最大最小蟻群算法來解決最優解搜索問題。

將蟻群算法應用到多表連接順序優化問題中時，要注意在每次選中連接表進行連接之后，對表的規模和連接進行重新計算。下面將詳細介紹并行最大最小蟻群算法應用到連接順序優化問題中的一般過程，包括：信息初始化、轉移概率計算、信息素更新、表規模更新以及并行化處理。

1)信息初始化。對各路徑信息素進行初始值設定，設φ表示初始信息素，令φ=C，其中為C常數。

2)轉移概率。對第t代循環，螞蟻個體Aij從節點i轉移到j的概率的可用式(7)計算：

(7)

其中：φij(t)表示邊(i,j)的信息素強度；α表示軌跡的相對重要性；β為期望的相對重要性；Wk表示一個關系表的集合，這個集合中的元素是所有還未被螞蟻k選擇的所有關系表；ηij(t)=1/Costij表示關系表i轉移到關系表j的期望程度，其中Costij表示兩個關系表連接的代價。

3)信息素更新。最大最小蟻群算法對傳統蟻群算法的改進之處在于改進信息素更新的方式。最大最小蟻群算法分別采用局部信息素和全局信息素來進行信息素的更新。其中，局部信息素可通過式(8)來進行更新，對每只螞蟻，只進行一次局部信息素的更新。

φij(t+1)=δφij(t)+(1-δ)Δφij(t)

(8)

在進行路徑搜索時，依照式(7)計算出的轉移概率，螞蟻會根據概率大小在可選集中選擇出下一步要連接的關系表。Δφij(t)模擬初始時刻連接邊(i,j)的信息素量;δ表示蒸發因子，它是一個0到1的常數。設置δ的目的是防止螞蟻由于過早收斂而陷入局部最優解。

最大最小蟻群算法在所有螞蟻完成連接之后，會搜索出一條當前代價最小的連接順序，經過這條連接順序的螞蟻個體被選擇成為最佳螞蟻。算法規定只有這些被選出的最佳螞蟻可以在經過的路徑上留下信息素。也就是說，最大最小蟻群算法對傳統蟻群算法的一個改進之處是增強最優解的信息素。同時，最大最小蟻群算法還會削減選出的最差路徑上的信息素強度，這個削減操作是為了保證螞蟻更快地集中到最優路徑周圍。最大最小蟻群算法的全局信息素更新方式可由式(9)～(12)表示。

(9)

(10)

(11)

(12)

其中φij(t+n)表示在所有螞蟻完成所有關系表的連接后得到的最優連接順序中邊(i,j)上的信息素；Lbest代表此次迭代過程中的最優連接順序的代價；Lworst表示此次迭代過程中最差連接順序的代價。

4)表規模更新。利用蟻群算法處理多表連接順序優化的過程中，不同于傳統旅行商問題的一點是：每次連接時，可選集中會刪除被連接的表，同時，被選中的表的規模會發生變化。將CAB表示為表A連接表B之后的表B的規模，即：|B|=CAB。表B中的屬性會與表A中的屬性集合并，表B的屬性規模可由式(13)計算，其中Attr表示A與B的公共屬性集合。

V(Attri,B)=

(13)

5)將最大最小蟻群算法運用到大規模數據表的多表連接查詢優化問題中時，算法的搜索時間比較長。針對這一缺陷，本文結合分布式數據庫并行性的特點對最大最小蟻群算法進行并行化處理，以達到更快獲得最優解的目的。最大最小蟻群算法的并行一般有兩種方式：細粒度的螞蟻并行方式和粗粒度的蟻群并行方式。前者以個體為并行單位，可通過消息傳遞和分布式共享內存的編程模型，以主從模式將螞蟻個體分配給不同的處理單元來實現并行化，但是這種并行方式會帶來處理單元之間頻繁的通信消耗；后者以種群為并行單位，也可以通過消息傳遞和共享變量兩種并行編程模型來實現，該方式將螞蟻種群分配給不同的處理單元來計算，減少了處理單元之間的消息傳遞。

本文的并行化是通過粗粒度的種群并行方式，采用基于共享變量模型的Pthread庫，將含有相同數量的蟻群分配給多個線程并行處理(設置蟻群數量相等是為了均衡處理單元的運算負載)，以提高搜索效率，從而提升Greenplum數據庫的查詢性能。并行最大最小蟻群算法相對于串行最大最小蟻群算法的區別在于，每個蟻群的螞蟻在經過局部信息素更新之后，會影響到所有蟻群的螞蟻的前進路線，因為信息素矩陣是被所有螞蟻共享的，但是局部信息素的更新會較頻繁地訪問信息素矩陣，導致同步操作增加而影響算法的運行效率，為此，本文對每只螞蟻進行限制，只進行一次局部信息素的更新。

最大最小蟻群算法并行化的過程如算法1所示。首先根據并行度同時運行數量相等的k只螞蟻的種群的迭代過程。對每一個種群，按照最大最小蟻群算法的搜索過程得到最優路徑。將所有種群的路徑提交給主線程之后，選擇更優的路徑，并更新全局信息素。迭代以上過程，直到得到最終的最優路徑。

算法1并行最大最小蟻群算法。

Input:n個表及其規模大小；

Output:最優連接順序。

1)

Initiation：并行度P，螞蟻數量K，α，β，全局迭代次數N1，局部迭代次數N2

2)

fori=1 toN1

//全局迭代

3)

do parallel

//并行化處理

4)

forj=1 toN2

//局部迭代

5)

fork=1 toK

//選擇擁有k只螞蟻的種群進行迭代

6)

初始化可選集Wk，信息素濃度φ；

7)

whileWk≠? do

8)

隨機選取Wk中的一個表A作為起點，將表A從Wk中刪除，更新Wk；

9)

計算轉移概率并根據結果選取一個表B與表A連接；

10)

修改被選中的表B的規模，|B|=CAB；局部更新信息素濃度；

11)

end while

12)

end for

13)

end for

14)

提交最優路徑；

15)

end do

16)

修改全局最優路徑，全局更新信息素濃度；

17)

end for

3　實驗結果及分析

實驗環境是Greenplum數據庫集群，該集群有4個節點：1個主節點，3個子節點。每個節點的實驗平臺均采用2.5 GHz雙核處理器，8 GB內存，CentOS 7操作系統，Greenplum數據庫的版本號是greenplum-db-gpdb-14b78f4。為了滿足對比實驗的公平性原則，基于MySQL數據庫與PostgreSQL數據庫的實驗都在8核的處理器上完成。

3.1　自主生成數據集實驗

為了驗證代價模型的有效性，本文利用Greenplum數據庫集群進行了如下實驗。首先在數據庫中生成5張關系表A、B、C、D和E，每張表的元組數分別為5×104、10×104、15×104、20×104和25×104。5張生成表的規模及屬性如表1所示。此外，本文通過多次實驗得到了并行最大最小蟻群算法的最優參數選擇，其中：螞蟻數量設置為30，局部迭代次數和全局迭代次數分別設置為20和30，并行度設置為2，代價模型中的權值設置為0.1。

表1　自主生成的表的規模(/104)及屬性Tab. 1　Size (/104) and attributes of the self-generated tables

初始的連接順序按從左至右為((AB)C)D)E)，獲取該連接的執行時間，然后利用并行最大最小蟻群算法找出代價最小的連接順序，即(((A(ED))C)B)，輸出這種方式的執行時間并且與其他連接方式的執行時間進行對比。表2中列出了其中5種連接方式的實際完成時間。對每種連接方式分別進行10次實驗，取平均值作為該連接順序進行連接的時間。從實驗結果可以看出，搜索出的最優連接順序完成連接所用的時間最少，這說明本文設計的代價模型可以比較準確地衡量不同連接順序的代價，驗證了該代價模型以及并行最大最小蟻群算法的有效性。

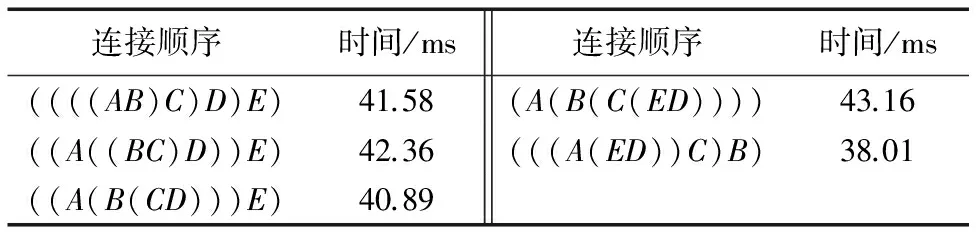
表2　連接操作的執行時間Tab. 2　Execution time of join operation

另一方面，為了驗證并行最大最小蟻群算法的尋優能力，本文分別利用動態規劃、最大最小蟻群算法、遺傳算法以及并行最大最小蟻群算法進行了多組對比實驗，上述四種算法獲得最優解的時間對比如圖1所示。可以看出，當連接關系數為5和10時，四種算法的尋優效率相差不大；隨著關系數的增加，遺傳算法和并行最大最小蟻群算法的效率相對其他兩種算法來說更高；當連接關系數增加到25時，并行最大最小蟻群算法的搜索效率相對遺傳算法來說更高，且隨著關系數的增多，這種優勢更加明顯。這說明并行最大最小蟻群算法的尋優能力比Greenplum數據庫定義的動態規劃和遺傳算法的效率更高。

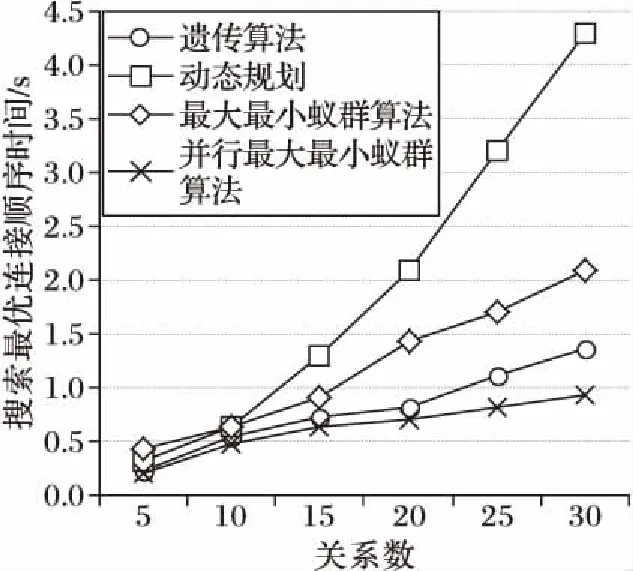
圖1　四種算法連接搜索最優連接順序的時間比較Fig. 1　Comparison of search time for optimal join order of four algorithms

3.2　標準數據集實驗

為了驗證基于代價模型的并行最大最小蟻群算法對Greenplum數據庫性能的優化，在Greenplum數據庫集群上模擬了復雜查詢。本節實驗的數據都是通過TPC-H工具得到的，其中測試數據量的統計如表3所示。

TPC-H是一套針對數據庫決策支持能力的測試基準，用來測試數據庫系統復雜查詢的響應時間，其中定義了一個數據庫模型,該模型包括8張數據表：CUSTOMER、LINEITEM、NATION、ORDERS、PART、PARTSUPP、REGION和SUPPLIER。針對這8張數據表提供了22條復雜的查詢語句，本文就通過執行這22條復雜查詢語句的時間長短來分析查詢效率，并展示前10條查詢語句的查詢時間。Greenplum、MySQL、PostgreSQL這三種數據庫處理查詢語句的時間對比結果如表4所示。從表4可以看出，MySQL數據庫對查詢語句的處理時間最長；而PostgreSQL相對MySQL的優勢則體現在算法的性能上，其采用的Hash join可以提高系統查詢的效率；但是，將PostgreSQL與Greenplum進行比較時，對于S3、S7和S8這三條查詢語句，PostgreSQL的處理時間更短。為了更精確地對PostgreSQL與Greenplum的性能進行對比分析，將8張數據表的規模放大10倍后再次對這兩個數據庫進行實驗。其中，前10條查詢語句的執行結果如表5所示。從表5可以看出，隨著數據量的增大，PostgreSQL的查詢時間顯著增加，性能下降比較明顯；但是，對S7這條查詢語句，PostgreSQL的執行時間仍然比Greenplum更短。這是因為，對少數一些查詢語句，Greenplum的重分布會消耗大量時間；同時，對比實驗的數據量還不足以模擬聯機分析處理(Online Analytical Processing, OLAP)場景，不能充分體現Greenplum對大數據處理的優勢。

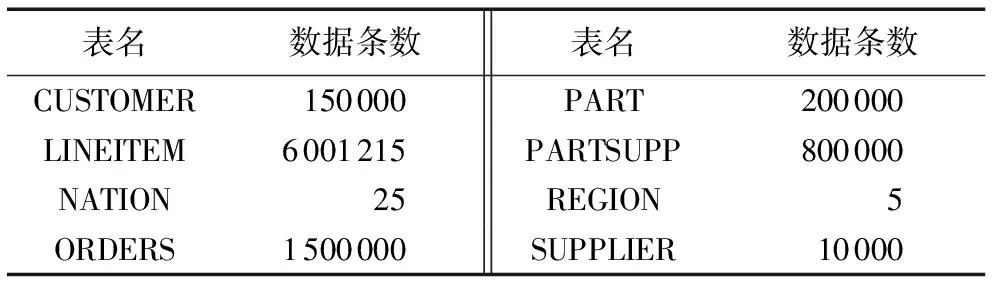
表3　各測試表的數據量統計Tab. 3　Data amount in each test table

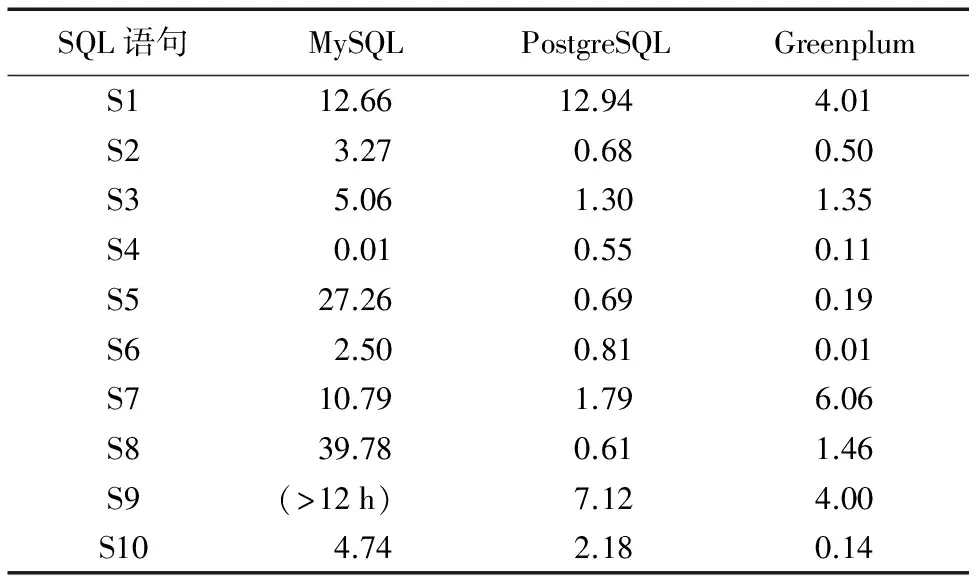
表4　三個數據庫的SQL語句執行時間對比　sTab. 4　Comparison of execution time for SQL statements of three databases　s

表6列出了Greenplum數據庫優化前和優化后的查詢語句執行時間對比,優化前后采用的表的規模是表1中規模的10倍。從表6中可以看出，優化后的Greenplum數據庫的平均查詢執行時間較優化前有所減少，查詢效率更高，但優化后的平均查詢執行時間減少幅度不大，原因在于本文實驗集群中每個子節點配置的僅是雙核CPU，雖然采用CPU內核調度可以提升CPU內核的利用率，但調度過程本身也會消耗時間；更主要的是Greenplum數據庫的查詢過程包括主節點將并行最大最小蟻群算法生成的最優查詢計劃分發給各子節點，分發過程涉及到廣播或重分布引起的子節點之間的數據傳輸，在數據規模不大的情況下，數據傳輸時間占據查詢執行時間的比重不可忽略，甚至對執行時間的影響較大。在內核數量少且查詢語句與數據量不大的情況下，優化后的Greenplum數據庫查詢性能提升不明顯，但較Greenplum優化前的查詢性能還是有所提升。

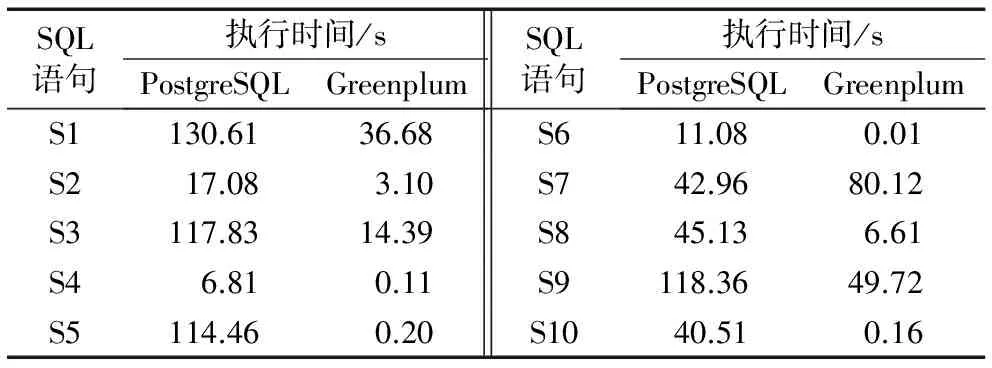
表5　兩個數據庫(規模放大10倍)的SQL語句執行時間對比Tab. 5　Comparison of execution time for SQL statements of two databases (data table scale ×10)

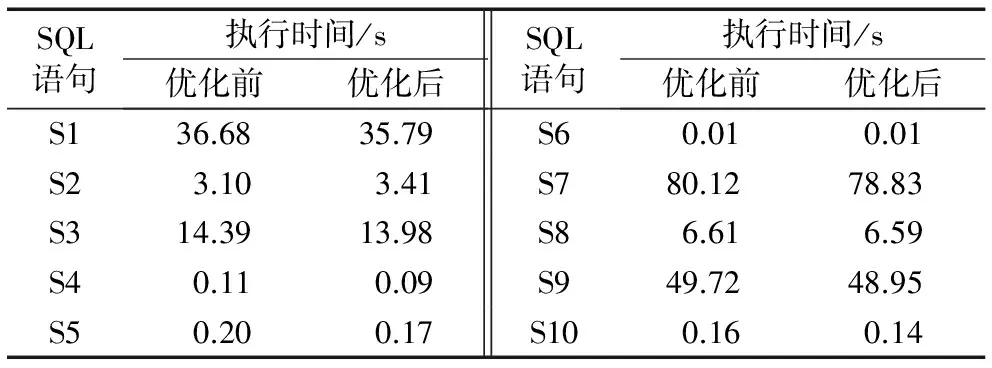
表6　Greenplum優化前后的SQL語句執行時間對比Tab. 6　Comparison of execution time for SQL statements of Greenplum before and after optimization

4　結語

為了解決分布式數據庫數據規模增大而導致的查詢效率降低的問題，本文對最優查詢計劃生成問題進行研究，提出了一種最優查詢計劃生成方法。連接順序執行時間、算法尋優能力、查詢語句執行時間的對比實驗表明，考慮了傳輸代價的代價模型能較準確地估計不同連接順序的代價，且基于該代價模型的并行最大最小蟻群算法在四種算法中擁有最好的尋優能力。由于實驗采用的查詢語句、表規模等數量上的有限性，優化后的Greenplum數據庫在查詢性能提升方面不是很明顯。在最優查詢計劃生成之后，為進一步提升Greenplum數據庫的查詢性能，對各節點之間的任務調度進行優化是下一步的研究方向。

參考文獻:

[1]ZENG F S. Research and improvement of database storage method [J]. Applied Mechanics and Materials, 2014, 608-609: 641-645.

[2]CHANG F, DEAN J, GHEMAWAT S, et al. Bigtable: a distributed storage system for structured data [J]. ACM Transactions on Computer Systems, 2008, 26(2): Article No. 4.

[3]GHEMAWAT S, GOBIOFF H, LEUNG S-T. The Google file system [C]// SOSP 2003: Proceedings of the 19th ACM Symposium on Operating Systems Principles. New York: ACM, 2003: 29-43.

[4]DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters [J]. Communications of the ACM — 50th Anniversary Issue: 1958—2008, 2008, 51(1): 107-113.

[5]GOLLAPUDI S. Getting Started with Greenplum for Big Data Analytics [M]. Birmingham: Packt Publishing, 2013: 24.

[6]ANTOVA L, EL-HELW A, SOLIMAN M A, et al. Optimizing queries over partitioned tables in MPP systems [C]// SIGMOD ’14: Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2014: 373-384.

[7]RODRIGUES E R, NAVAUX P O A, PANETTA J, et al. A comparative analysis of load balancing algorithms applied to a weather forecast model [C]// SBAC-PAD 2010: Proceedings of the 2010 22nd International Symposium on Computer Architecture and High Performance Computing. Washington, DC: IEEE Computer Society, 2010: 71-78.

[8]KOSSMANN D, STOCKER K. Iterative dynamic programming: a new class of query optimization algorithms [J]. ACM Transactions on Database Systems, 2000, 25(1): 43-82.

[9]ILAVARASAN E, THAMBIDURAI P. Genetic algorithm for task scheduling on distributed heterogeneous computing system [J]. International Review on Computers & Software, 2015, 1(3): 233.

[10]KUMAR T V V, SINGH V, VERMA A K. Distributed query processing plans generation using genetic algorithm [J]. International Journal of Computer Theory and Engineering, 2011, 3(1): 1793-8201.

[11]HANAFY H A, GADALLAH A M. Ant colony-based approach for query optimization [C]// DMBD 2016: Proceedings of the 2016 International Conference on Data Mining and Big Data, LNCS 9714. Cham: Springer, 2016: 425-433.

[12]HOOS H H, STüETZLE T. Special issue on stochastic search algorithms — Preface [J]. Annals of Operations Research, 2007, 156: 1-4.

[13]SOLIMAN M A, ANTOVA L, RAGHAVAN V, et al. Orca: a modular query optimizer architecture for big data [C]// SIGMOD 2014: Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2014: 337-348.

[14]GIRI A K, KUMAR R. Distributed query processing plan generation using iterative improvement and simulated annealing [C]// IACC 2013: Proceedings of the IEEE 3rd International Advance Computing Conference. Piscataway, NJ: IEEE, 2013: 757-762.

[15]MAHMOUD F, SHABAN S, ABD EL-NABY H. A proposed query optimizer based on genetic algorithms [J]. Egyptian Computer Journal, 2010, 37(1): 1-22.