正六面體工裝誤差對光纖慣組加速度計零偏標定精度影響分析

姚　勤，胡夢純，何子輝

(1.海軍駐上海地區航天系統軍事代表室，上海201109; 2. 上海航天控制技術研究所，上海201109; 3.上海慣性工程技術研究中心,上海201109)

0　引言

陀螺和加速度計是慣性測量組合的核心元件。慣性測量組合性能的好壞直接影響導航精度。要提高慣組的使用精度，一方面要提高陀螺和加速度計的自身精度，另一方面還需要提高慣組的標定精度。提高標定精度需要分析各誤差源對標定參數產生的影響，對基于大理石平板正六面體工裝的標定進行分析，六面體工裝的精度會對標定結果產生影響。本文通過評估工裝精度對標定結果影響的量化關系，提出一種減小工裝誤差影響的光纖慣組標定解算方法。文獻[1]、文獻[2]針對轉臺誤差對標定結果的影響進行分析[1-2]，文獻[3]研究了基于離心機的IMU標定及誤差分析方法[3],而本文使用的標定方法并未使用轉臺和離心機，而是采用大理石平板與正六面體工裝進行標定，針對正六面體工裝誤差的文獻涉及較少，有必要分析該方法中正六面體工裝誤差導致的標定誤差。

1　光纖慣組輸入輸出數學模型

標定模型對于標定方法的選擇、IMU性能評估以及系統的誤差分配具有重要意義[4]，下面討論光纖慣組的標定數學模型。

光纖慣組中的陀螺和加速度計分別為光纖陀螺和石英撓性加速度計，工程上通常使用一階線性方程描述光纖陀螺和石英撓性加速度計的誤差模型。分別對陀螺儀和加速度計建立輸入輸出數學模型[5-6]。

光纖陀螺標度因數非線性高，正負不對稱性好，零偏穩定性好，因此可將陀螺單表的輸入輸出模型近似描述為一階形式。陀螺組合輸入輸出模型用一階線性方程描述為：

(1)

式中：Ngx、Ngy、Ngz為各軸陀螺單位時間輸出的脈沖數，單位bit/s；kgx、kgy、kgz為各軸陀螺的標度因數，單位bit/(°)；Egqp(p、q=x，y，z)為慣組各測量軸相對各軸陀螺敏感軸由于安裝誤差導致的交耦系數，簡稱安裝誤差；Egqp為慣組p軸相對q軸陀螺的耦合；Dgx、Dgy、Dgz為各軸陀螺的零偏，單位(°)/s；ωx、ωy、ωz為外施角速率在慣組x、y、z軸上的分量，單位(°)/s。

加速度計二次項系數忽略不計，加速度計組合輸入輸出模型用一階線性方程可表示為：

(2)

式中：Nax、Nay、Naz分別為各軸加速度計單位時間輸出的脈沖數，單位bit/gs；kax、kay、kaz分別為各軸加速度計的標度因數，單位bit/gs；Eaqp(p、q=x，y，z)為慣組各測量軸相對各軸加速度計敏感軸由于安裝誤差導致的交耦系數，簡稱安裝誤差；Eaqp為慣組p軸上的輸入對q軸加速度計的耦合；Dax、Day、Daz為各軸加速度計的零偏，單位g；fx、fy、fz為外施加速度在慣組x、y、z軸上的分量，單位g。

2　基于大理石平板正六面體工裝的標定與解算

慣組的標定方法有利用轉臺的方法[7-8],利用六面體工裝的方法[9],使用攝影技術的方法[10],基于多位置旋轉的現場標定法[11]等，用標定方法多為速率法與位置法，位置法又分為6位置法[12-13]、12位置法[5-6]、20位置法[14]等。

基于大理石平板正六面體工裝的標定方法采用了速率法與位置法，速率法采用在高精度大理石平板上手動正反轉3圈的方式進行標定，位置法為12位置法。速率法可標定出陀螺標度因數、安裝誤差[15]；位置法可標定出陀螺零偏、加表標度因數、安裝誤差、零偏。本文主要對正六面體工裝誤差對加速度計標定零偏誤差的影響進行分析，因此僅分析位置法。

位置法編排為12位置，初始位置為天東北，按照X軸朝天、X軸朝地、Y軸朝天、Y軸朝地、Z軸朝天、Z軸朝地的順序對12位置進行排列，得到標定順序，如表1所示。

表1　12位置標定順序

將12位置加速度計和陀螺儀輸入代入模型中，利用最小二乘法可以求出：

(3)

(4)

(5)

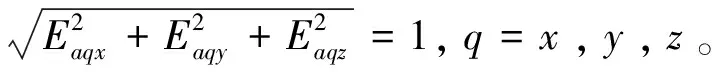
歸一化可得各軸加速度計標度因數為

(6)

式中：q=x，y，z。

各軸加速度計安裝誤差為

Eaqp=Kaqp/kgq

(7)

式中：j=1～12；p=x，y，z；q=x，y，z。

根據加速度計各位置各軸輸出可得

可求得各軸加速度計零偏為

(8)

式中：j=1～12，q=x，y，z。

還有一種零偏的計算方法為12位置二向法，求各軸零偏時，只考慮敏感軸朝天朝地的位置進行解算。

(9)

(10)

(11)

3　標定誤差分析

慣組測試標定用工裝為六面體，慣組標定時需要安裝在六面體工裝內，再在大理石平板上進行標定。六面體工裝外表面由6個基準面組成。六面體內由1個或多個安裝基準面組成，這些安裝基準面能夠保證每次慣組安裝在六面體工裝內的一致性，本文不對六面體內的基準面誤差以及大理石平板的誤差影響進行分析。

假設六面體工裝是以底面C為基準加工其他表面，表2所示為六面體工裝各面需加工的精度項目及引起的誤差角。根據慣組測試標定的誤差模型進行12位置法翻轉時會引入工裝的誤差，直接影響慣組測試標定結果，使得加速度計的標定結果變差，具體分析如表2表示。

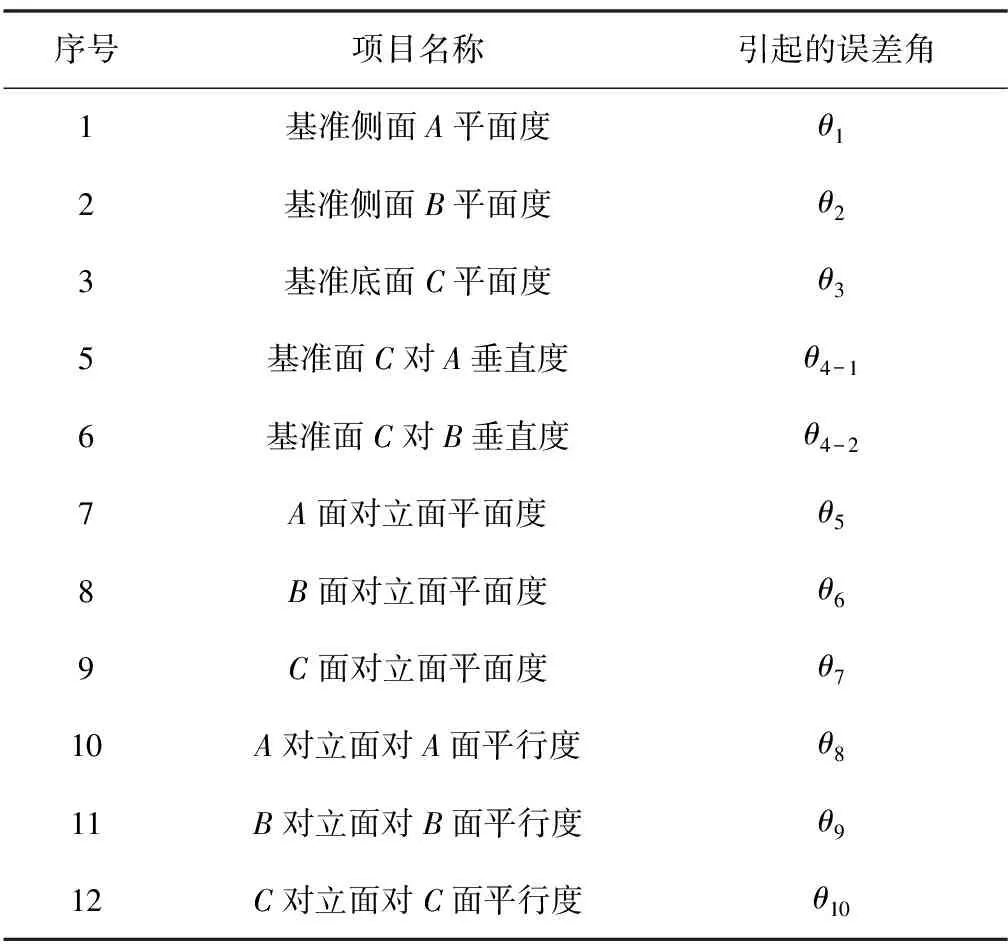
表2　六面體工裝誤差項目

假設慣組X軸向垂直C面，指向C面對立面；Y軸向垂直A面，指向A面對立面；Z軸向垂直B面，指向B面對立面，具體如圖1所示。

對六面體工裝精度對12位置法標定中加表零偏值的影響進行分析，根據表2，考慮六面體工裝誤差時各位置加速度計各軸的參考輸入如表3所示。

表3　十二位置標定各軸參考輸入

將各軸參考輸入加速度代入加表組合模型中，可得加表的采樣輸出如式(12)

(12)

式中，加表輸出為采樣輸出，標度因數、安裝誤差、零偏均為真實值。為簡化分析，令表1中各誤差角均設置為等值θ。解算標定參數時，根據第3節中的公式，可推導出考慮六面體工裝誤差后標定出的零偏測量如下。

12位置法

(13)

12位置二向法

(14)

(15)

(16)

12位置法解算出的零偏誤差為

(17)

12位置二向法解算出的零偏誤差為

(18)

忽略小量，可推知兩種零偏算法的誤差值分別為：

(19)

ΔDa2≈0

(20)

12位置解算方法中引入的誤差與工裝精度成正比，12位置二向法中引入的誤差均為小量，可忽略不計。

由理論推導可知，當考慮六面體工裝誤差時，12位置法解算出的零偏會引入六面體工裝誤差，而采用12位置二向法解算出的加表零偏基本不引入六面體工裝誤差。

4　仿真分析與驗證

對12位置標定進行仿真，加速度計測量噪聲設置為10μg高斯白噪聲。正六面體工裝長度為400mm，六面體工裝誤差項目中平面度、垂直度、平行度均為0.04。按表1所示12位置，每個位置靜態采集100s，采樣周期20ms，用于加速度計標度因數、安裝誤差、零偏的標定，加速度計標定參數真值設定如表4所示，仿真結果如表5所示，標定結果誤差對比如表6所示。

表4　加速度計標定參數真值設定

表5　加速度計標定參數仿真結果

表6　零偏誤差對比

由仿真結果可以看出，考慮六面體工裝誤差的情況下，用12位置法解算出的零偏與真值偏差比用12位置二向法解算出的零偏與真值偏差大。

5　結論

本文針對采用大理石平板正六面體工裝對慣組12位置法標定進行分析，考慮工裝誤差，量化分析并比較了采用兩種解算方法時工裝的精度對加表零偏產生的影響，為如何根據標定精度要求反提工裝精度要求提供理論依據，并提出了一種減小加表零偏標定誤差的解算方法。

當長寬高為400mm的工裝平面度、垂直度、平行度誤差均為0.04時，采用12位置法解算加速度計零偏的標定誤差達到0.0001g量級；而采用12位置二向法解算加速度計零偏，誤差為10-7g量級。可以看出，12位置二向法解算出的加速度計零偏誤差遠小于采用12位置法解算出的加速度計零偏誤差。為減小工裝誤差的影響，解算加速度計零偏時可采用12位置二向法。

[1]丁楓,馮麗爽，晁代宏，等.轉臺安裝誤差對光學捷聯慣導標定的影響分析[J].彈箭與制導學報,2013,33(1):19-24.

[2]聶夢馨, 呂品, 賴際舟,等. 一種光纖IMU的雙軸非定向標定方法[J]. 電子測量技術, 2014, 37(8):123-128.

[3]趙剡, 張少辰, 胡濤. 慣性測量組件離心機標定及誤差分析方法[J]. 北京理工大學學報, 2015, 35(4):414-420.

[4]趙桂玲, 姜雨含, 李松. IMU標定數學建模及誤差分析[J]. 傳感技術學報, 2016, 29(6):886-891.

[5]胡夢純, 徐挺, 黃云柯,等. 冗余結構光纖陀螺捷聯慣組標定優化方法研究[J]. 上海航天, 2016, 33(s1):134-139.

[6]魏莉莉, 黃軍, 傅長松,等. 帶斜置元件的光纖陀螺捷聯慣組標定方法[J]. 中國慣性技術學報, 2015(1):14-19.

[7]李政, 張志利, 周召發. 基于雙軸位置轉臺的光纖陀螺慣組標定方法[J]. 壓電與聲光, 2016(4):607-610.

[8]童樹兵, 張志利, 周召發,等. 一種基于雙軸位置轉臺的IMU快速標定方法[J]. 壓電與聲光, 2016, 38(5):815-818.

[9]彭孝東, 張鐵民, 李繼宇,等. 三軸數字MEMS加速度計現場標定方法[J]. 振動、測試與診斷, 2014, 34(3):544-548.

[10]江來偉, 崔希民, 袁德寶,等. 慣性測量單元基準面與載體平臺的標定方法研究[J]. 測繪工程, 2015(3):16-20.

[11]王堅, 梁建, 韓厚增. 低成本IMU的多位置旋轉現場標定方法[J]. 中國慣性技術學報, 2017, 25(3):294-298.

[12]烏偉, 趙嚴, 寧永權,等. 微慣性測量單元的標定技術研究[J]. 電光與控制, 2013(8):54-57.

[13]李璞, 王麗華, 李明. 重復標定的慣組誤差模型系數計算方法[J]. 導彈與航天運載技術, 2012(3):34-37.

[14]董春梅, 任順清, 陳希軍. 基于三軸轉臺誤差分析的IMU標定方法[J]. 系統工程與電子技術, 2016, 38(4):895-901.

[15]林強. 高精度光纖陀螺標度因數測試研究[J]. 現代導航, 2013(3):186-190.