混合FE-WBM的聲學預測方法?

張志飛，梁 濤，徐中明，夏小均，陶能發

前言

目前，聲學的數值分析方法主要是基于單元技術的有限元法(FEM)、邊界元法(BEM)、統計能量法(SEA)和它們的混合建模方法。由于有限元法和邊界元法是基于單元的方法，因此隨著分析頻率的增加，為保證求解精度，網格尺寸必須減小，從而導致求解模型隨著分析頻率的增加而迅速增加，因此，有限元法大多是用于低頻分析中[1-2]。而統計能量法由于其高模態密度的要求，只能在高頻范圍內使用，此外，統計能量法是一種統計方法，因此它是非確定性預測方法[3]。目前在中頻段缺乏廣泛應用的確定性中頻預測方法。

WBM是以Trefftz理論為基礎推導而來的間接Trefftz方法[4]。WBM不需要對結構和聲域劃分網格[5]，而是采用嚴格滿足控制微分方程的波函數的線性疊加來描述系統的動態響應變量[6-7]，該方法在求解區域內不存在近似誤差，但是有可能不滿足邊界條件和連續性條件，為此該方法采用加權余量公式使其在邊界和連續界面處的加權余量等于零，這樣就能構造一個矩陣方程組，通過計算即可得到基波函數的加權系數，從而求得系統的響應[8]，因此，WBM具有模型規模小的特點。此外，WBM還具有高收斂性，與FEM相比其計算效率更高，故可以應用于更高頻率范圍的聲學分析預測[9-11]。但是，WBM收斂的一個充分非必要條件是所求聲域為凸形域，因此其幾何適應能力遠不如FEM。

針對車內聲腔這類邊界幾何復雜的非凸形域內部聲學問題，無法滿足WBM求解域為凸形域的收斂條件。若采用FEM，為保證求解精度，隨頻率增加網格尺寸要求越精細，導致模型規模迅速增大，計算的時間成本急劇增加，從而限制了其在更高頻率范圍的應用。針對上述兩種方法的特點，為高效的實現此類復雜幾何域的中低頻聲學響應，本文中以聲壓和法向速度為連續性條件，采用了兼具兩種數值方法優點的混合FE-WBM方法，并完成其理論推導。以某二維車內聲域為例，運用混合方法建立了數值求解模型。通過與傳統有限元方法的對比，驗證了混合FE-WBM的正確性與高效性。

1　聲學問題

對內部有源的凸形封閉聲學空間Ω，任意位置r的穩態聲壓p滿足Helmholtz控制方程[12]:

對于內部聲學問題，如圖1所示，邊界Γ由3部分構成(Γ＝Γp∪Γv∪Γz)，在Γp邊界施加聲壓p，在Γv邊界施加法向速度vn，在Γz邊界施加法向阻抗Z[13]，即

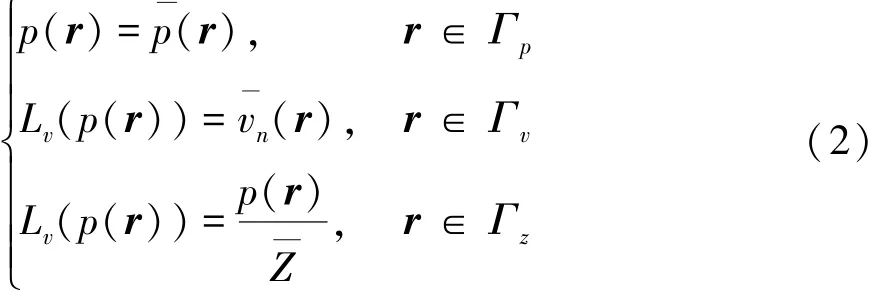
1.1　聲學有限元法

圖2是有界聲腔Ω的網格，每個單元Ωe的邊界由4部分組成，即Γe＝Γep∪Γev∪Γez∪Γei。Γep，Γev和Γez是聲學邊界與單元邊界的交集(Γep＝Γe∩Γp，＝Γe∩Γv，Γez＝Γe∩Γz)，Γei表示相鄰單元的公共邊界。

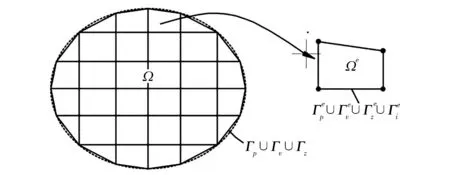
圖2　有限元劃分與單元定義

在每個單元Ωe內部，采用簡單基函數的線性組合p＾(r)來近似代替其精確解p(r):

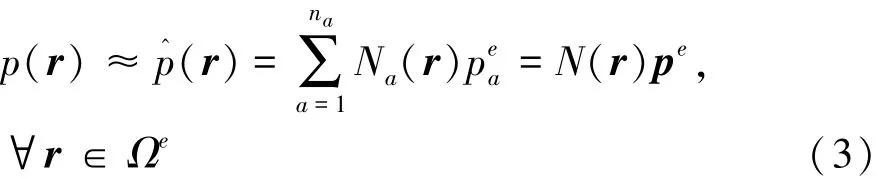
式中:貢獻因子pea組成的列向量pe是未知的自由度，即節點聲壓。

在相鄰單元的公共界面施加速度連續性條件，得到的單元模型為

式中:Ze＝ - ω2Me＋ jωCe＋ Ke；fe＝jω(qe-ven-是成對出現，在組裝整體FE模型中相互抵消。將所有的單元矩陣組合便得到整個模型的FE模型:

式中:Z＝ -ω2M ＋jωC ＋K；f＝ jω(q-vn)；M，C和K分別表示聲學質量、阻尼和剛度矩陣；q和vn分別表示與點生源q和法向速度vn相關的載荷向量。

1.2　聲學波函數法

WBM是采用全局Trefftz基函數Ψa和聲壓特解函數的線性組合p＾來近似聲壓精確解p:

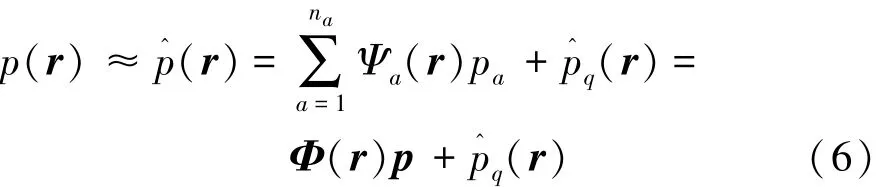
式中:行向量Φ由Trefftz基函數Ψa組成，列向量p是由未知加權系數pa組成，na表示波函數的個數。本文中選取的聲學基函數[14]為

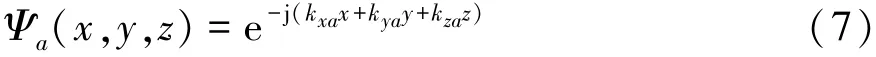
式中kxa，kya和kza滿足如下關系:

聲腔中rq處放置一聲源時，在r處的聲壓特解函數為

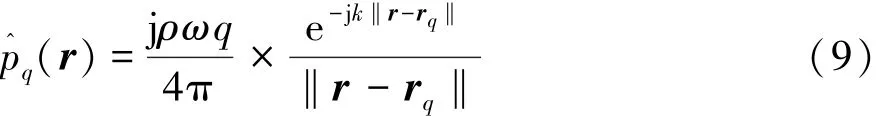
理論上，當波數趨于無窮大時，式(6)的解收斂于精確解，但在數值計算中僅能取有限數目的基波函數，因此需要采用截斷法則。

基于SPIEGEL針對半幅傅里葉級數提出的理論，即余弦函數的最小周期不應大于其近似函數周期的一半，即截斷系數T≥2。最小空間周期λi，min和聲波波長λ定義為

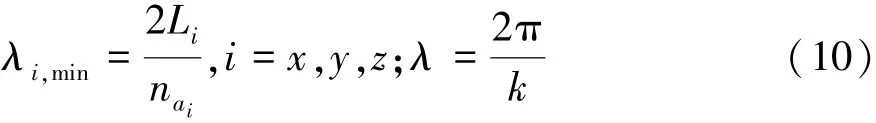
式中Li(i＝x，y，z)表示包含求解域最小立方體在x，y，z方向的物理尺寸。

故截斷法則Tλi，min≤λ可表示為

近似聲壓p＾(r)滿足Helmholtz方程，因此，通過加權積分使壓力近似值p＾(r)滿足式(2)中的邊界條件，從而得到波模型，求解后便可得到未知波函數加權系數p。加權余量公式為

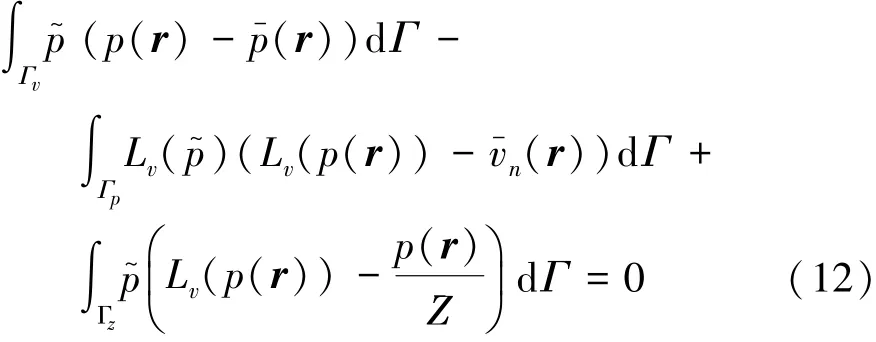
其中:

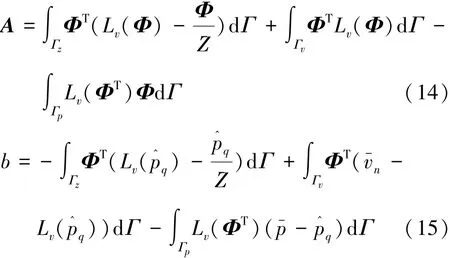
2　混合有限元-波函數法

為實現復雜系統在中頻的高效、高精度聲學預測，采用了充分結合FEM和WBM各自優勢的混合FE-WBM。FE-WBM的基本思想是將WBM用于大型均勻的簡單幾何體，充分利用WBM數值模型小、計算效率高的特點，同時將FEM用于幾何復雜的區域，充分利用FEM較強的幾何適應能力，最終創建的混合FE-WBM模型的自由度將比純FEM模型大幅減少，在提高模型計算效率的同時，保證了模型的良好幾何適應性。在FE(finite element)域和WB(wave based)區域的耦合界面處Γi，采用壓力連續和法向速度連續的耦合條件[15]，即將壓力連續性條件以邊界條件的形式施加到WBM區域，同時將法向速度連續性條件施加到耦合界面的FEM側，如圖3所示，即

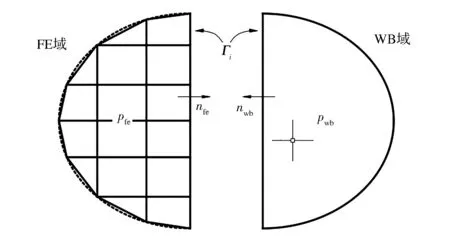
圖3　FE-WB直接耦合方式

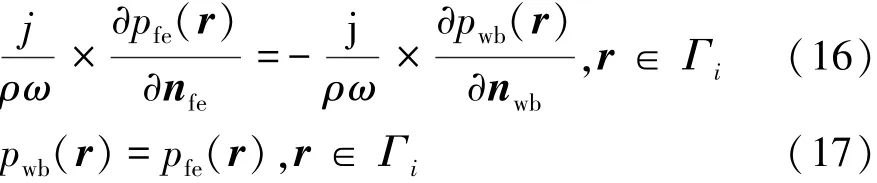
混合模型的FEM部分為

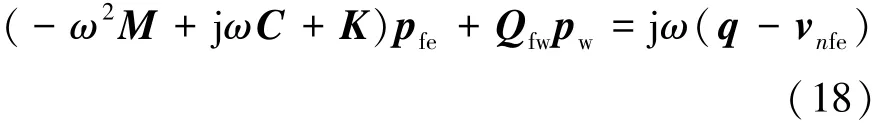
令 Zfe＝-ω2M ＋jωC ＋K，ffe＝jω(q-vnfe)，則上式可表示為

式中:Qfw為FEM對WBM的耦合矩陣；pw為波函數的加權系數矩陣。

混合模型的WBM部分為

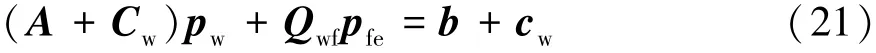
其中:

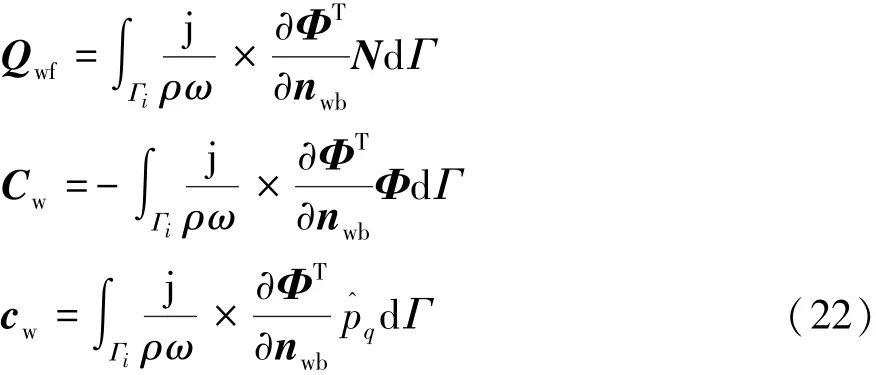
式中:Qwf為WBM對FEM的耦合矩陣；Cw和cw分別為WBM的反饋矩陣和反饋向量。

由式(18)和式(21)得到FE-WBM耦合模型:

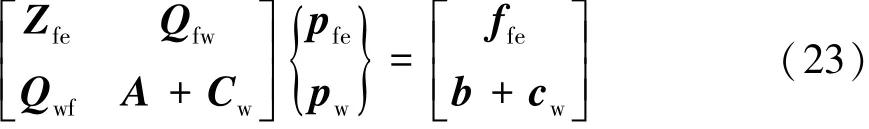
求解式(23)便可得到有限元部分的節點壓力pfe和 pw。

式(23)的系數矩陣不再是帶狀稀疏矩陣，因此若采用直接法求解方程組，求解效率低且未充分利用有限元矩陣Zfe的帶狀稀疏特性。因此，將式(23)的求解分為以下步驟[16]。

(1)將pw視為已知，求解節點聲壓矩陣pfe:

將式(24)帶入式(21)，整理得

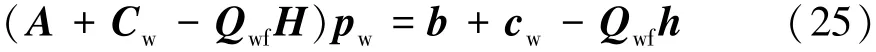
通過求解如下兩個線性方程得到矩陣H和h:

因為Zfe是帶狀稀疏矩陣，因此可以采用高度優化的稀疏帶狀矩陣求解算法。

(2)求解式(25)，得到 pw。

(3)節點聲壓矩陣pfe為

3　數值算例

為驗證上述方法的可行性，建立了一個簡化后的二維車內聲腔模型，如圖4所示。由圖可知，車內聲腔的邊界幾何較復雜，尤其是在聲腔與座椅的交界處。如前所述若想采用WBM，則必須將其求解域劃分為互不重疊的凸形域，然而該聲腔與座椅交界處的幾何形狀復雜，且座椅頭枕等區域無論如何劃分都無法保證其WBM子域為凸形域，因此僅采用WBM法是不可行的，但可以采用混合FE-WBM數值方法求解該車內聲腔的聲壓響應。將幾何較復雜的座椅區域附近采用FEM，幾何較簡單的其余區域采用WBM，如圖5所示。圖中填充區域表示采用有限元法的區域，未填充區域表示采用波函數法的區域，虛線表示各個區域之間的公共邊界，將整個車內聲腔劃分為4個WB域和一個FE域。速度邊界施加在WB域，聲壓響應點在FE域。在左側邊界上施加法向速度v-n＝10m/s，其余邊為剛性壁邊界，即法向速度為零。介質為空氣，其材料參數:密度ρ＝1.225kg/m3，聲速c＝340m/s。聲壓響應點取為駕駛員耳朵附近。

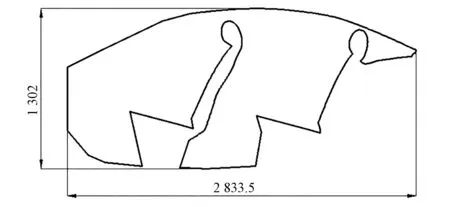
圖4　車內聲腔模型

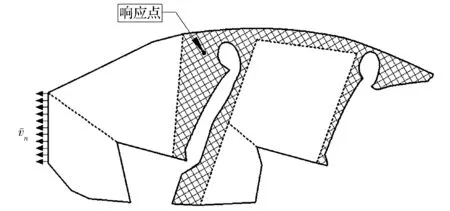
圖5　車內聲腔區域劃分

3.1　結果分析

FE-WBM混合模型中，WBM的截斷參數T＝4.0，各WB域之間在耦合邊界處采用速度-聲壓連續性條件。為說明FE-WBM的有效性，建立了由4 936個線性四邊形單元組成的粗有限元模型和由12 669個線性四邊形單元組成的精細有限元模型，并將精細有限元模型作為參考模型。各模型在600和900Hz的聲壓分布云圖如圖6和圖7所示。圖6(b)和圖7(b)中的虛線是聲腔區域劃分線，車內聲腔聲壓分布云圖連續，在各WBM子域與FEM域的公共邊界處壓力分布連續，未出現明顯的畸變。從600和900Hz各模型的聲壓云圖對比可知，FE-WBM模型和參考模型的計算結果，無論是聲壓分布還是聲壓數值上均符合得較好，而粗有限元模型與參考模型的聲壓分布存在一些差異，在900Hz時差異較600Hz時的更加明顯。

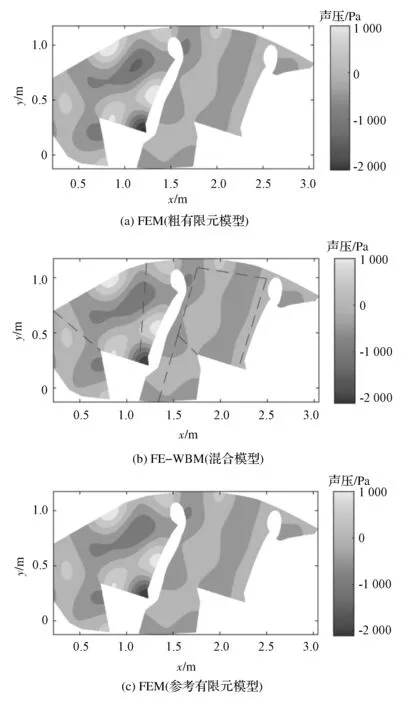
圖6 600Hz時聲壓分布云圖

圖8(a)和圖8(b)分別是二維車內聲腔中響應點在1～1 000和500～1 000Hz的聲壓頻率響應曲線。由圖8(a)可知，在1～1 000Hz內，三者的整體趨勢一致，FE-WBM與參考模型的計算結果，除在個別頻率附近存在一些頻率和幅值的偏差外，在整個頻率范圍內均符合得較好。而粗有限元模型在稍高頻率范圍內相對參考模型出現明顯的頻率偏移，這一點在圖8(b)中更加直觀。通過聲壓分布云圖和聲壓響應點頻率響應曲線說明FE-WBM的計算結果精度較高。

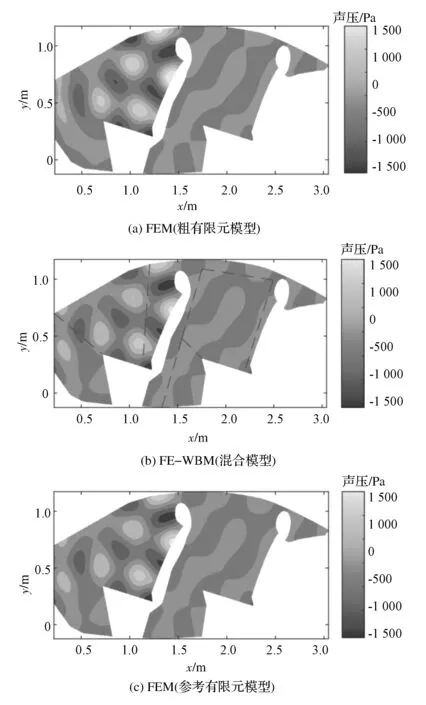
圖7　900Hz時聲壓分布云圖

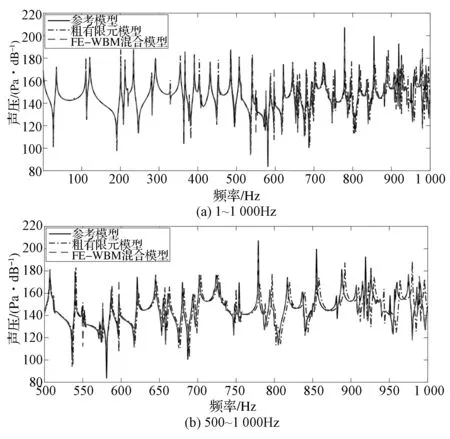
圖8　二維車內聲腔響應點聲壓頻響曲線

3.2　收斂性分析

為比較各方法的計算精度和效率，分析了290Hz時混合FE-WBM與FEM模型的聲壓響應收斂性。相對聲壓誤差[14]定義為

式中:p＾表示混合FE-WBM或FEM計算的響應點聲壓；pref表示參考聲壓，即精細有限元模型計算的響應點聲壓。

混合FE-WBM模型和FEM模型均是在i5-6500CPU(3.20GHz)，8GB運行內存，64位操作系統，Mat lab R2016a平臺運行。圖9和圖10分別為290Hz時相對聲壓誤差隨模型自由度和CPU運行時間增加的變化曲線。雖然WBM的收斂性隨著域分解的增加會有所下降[4]，但從圖9和圖10可知，達到相同的計算精度，FE-WBM的模型自由度和CPU運行時間較FEM依然存在明顯的優勢。

可見，采用FE-WBM時，將FEM應用于幾何復雜的區域，WBM用于簡單幾何的區域，在保證其良好的幾何適應能力的同時也保證了計算精度和效率，因此混合FE-WBM可用于更高頻率的分析。

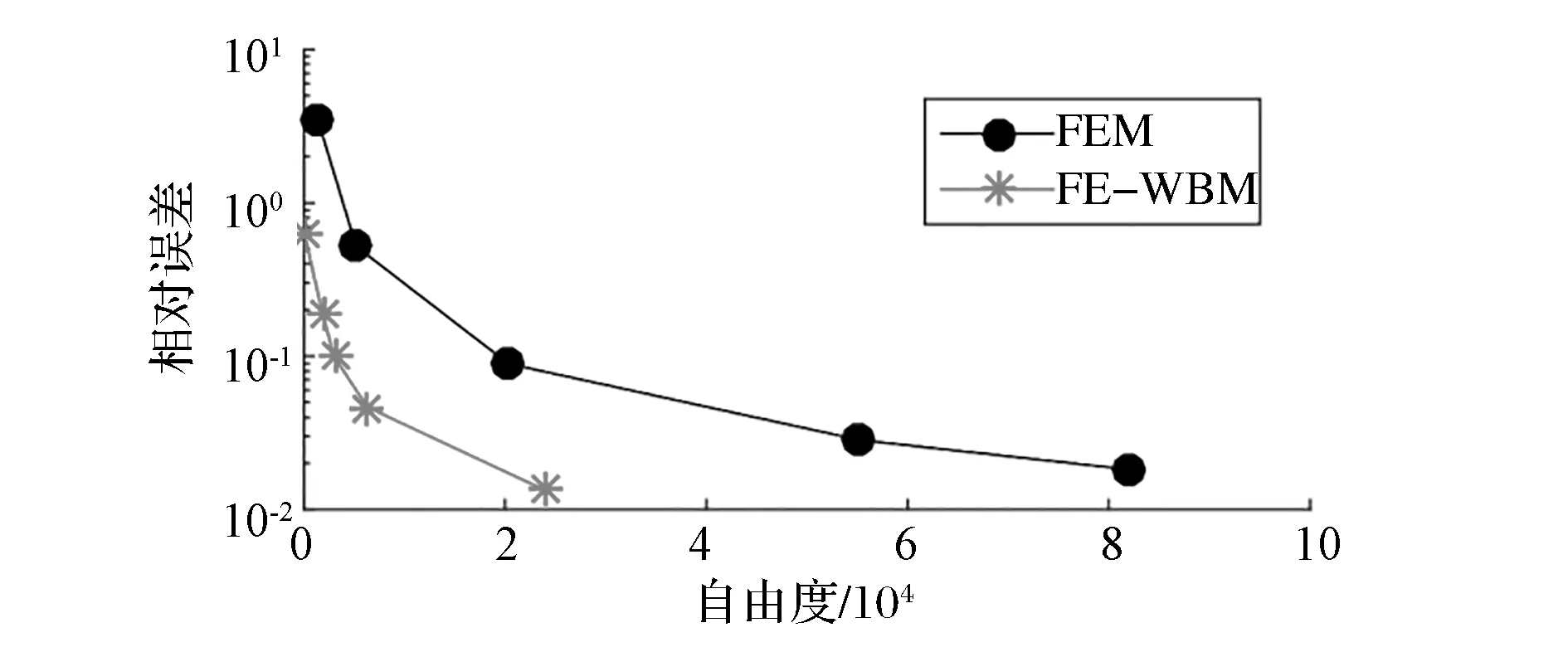
圖9　相對誤差-自由度收斂曲線

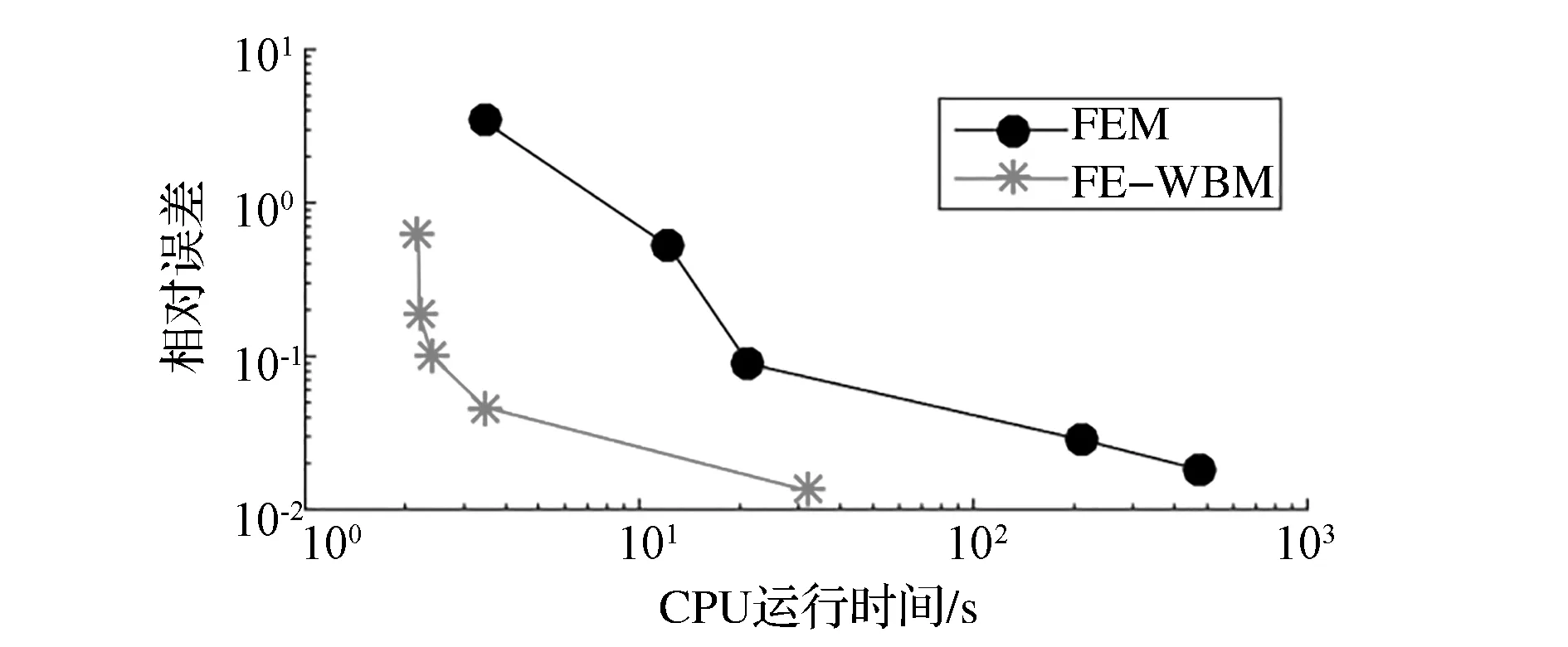
圖10　相對誤差-CPU運行時間收斂曲線

4　結論

本文中采用結合FEM的強幾何適應能力和WBM的高收斂率的FE-WBM，通過聲壓和法向速度連續性條件實現二者的耦合。以簡化后的二維車內聲腔模型為例，將幾何復雜的區域采用FEM，將幾何簡單的區域采用WBM，建立了二維聲腔的混合FEWBM模型。通過對比粗有限元、精細有限元和混合FE-WBM的聲壓云圖和響應點聲壓頻率響應曲線，證明了FE-WBM的有效性。通過收斂性分析，說明了FE-WBM相對FEM的高收斂率，且FE-WBM中有限元部分的網格越精細，其計算精度越高，與此同時計算時間雖有所增加，但相對FEM依然存在明顯的優勢。今后的工作是將混合FE-WBM用于三維聲腔和結構-聲學耦合系統分析中。

[1] 高印寒，張澧桐，梁杰，等.基于聲-固耦合模型的車內噪聲響度參數的預測與分析研究[J].機械工程學報，2016，52(12):136-143.

[2] 徐中明，何治橋，賀巖松，等.車內低頻噪聲預測模型的改進[J].汽車工程， 2016，38(7):878-882.

[3] MACE B，DESMET W，PLUYMERSB.Mid-frequency methods in sound and vibration-part A[J].Journal of Sound&Vibration，2013，332(8):1895-1896.

[4] WIM D.A wave-based prediction technique for coupled vibro-acoustic analysis[D].Leuven:University of Leuven，1998.

[5] DECKERSE，ATAK O，COOX L，et al.The wave based method:an overview of 15 years of research[J].Wave Motion， 2014，51(4):550-565.

[6] KITA E，KAMIYA N.Trefftz method:an overview[J].Advances in Engineering Software， 1995，24(1-3):3-12.

[7] BERGEN B，VAN GENECHTEN B，VANDEPITTE D，et al.An efficient trefftz-based method for three-dimensional helmholtz problem in unbounded domains[J].CMES， 2010，61(2):155-175.

[8] PLUYMERS B，VAN HAL B，VANDEPITTE D，et al.Trefftzbased methods for time-harmonic acoustics[J].Archives of Computational Methods in Engineering， 2007，14(4):343-381.

[9] DESMET W，HAL B V，SASP，et al.A computationally efficient prediction technique for the steady-state dynamic analysis of coupled vibro-acoustic systems[J].Advances in Engineering Software，2002，33(7):527-540.

[10] PLUYMERSB，DESMET W，VANDEPITTE D，et al.Application of an efficient wave-based prediction technique for the analysis of vibro-acoustic radiation problems[J].Journal of Computational and Applied Mathematics， 2004，168(1-2):353-364.

[11] VERGOTE K，VANMAELE C，VANDEPITTE D，et al.On the use of an efficient wave based method for steady-state structural dynamic analysis[C].Proceedings of LSAME.08.Leuven，Belgium:KU Leuven Press，2008:433-459.

[12] 何雪松.結構—聲學耦合分析及其波函數法研究[D].武漢:華中科技大學，2008.

[13] MARESSA A，JONCKHEERE S，VAN GENECHTEN B，et al.Hybrid finite element-wave based techniques for interior vibro-acoustics.application to a large-sized vehicle model[C].Proceedings of ISMA2012-USD2012.2012，8(12):3927-3940.

[14] VAN HAL B，DESMET W，VANDEPITTE D，et al.Hybrid finite element-wave based method for acoustic problems[J].Computer Assisted Mechanics and Engineering Sciences， 2003，10(4):375-390.

[15] PLUYMERS B.Wave based modelling methods for steady-state vibro-acoustics[M].2006D04.Leuven:KU Leuven，2006.

[16] PLUYMERS B，DESMET W，VANDEPITTE D，et al.Wave based modelling methods for steady-state interior acoustics:an overview[C].Proceedings of ISMA2006.Leuven，Belgium:KU Leuven Press，2006:2303-2358.