基于學生現(xiàn)實,對接“思維關口”
江蘇儀征市實驗小學西區(qū)校(211900)
數(shù)學是一門邏輯性、系統(tǒng)性很強的學科,教師要立足學生現(xiàn)實,從學情出發(fā),抓住思維關口,從知識的生長點、延伸點、易混點三個方面入手,關聯(lián)數(shù)學知識各部分之間的關系,結合學生已有知識,進行遷移、重組和改造。現(xiàn)我根據(jù)自己的教學實踐,談談對這一問題的思考和體會。
一、基于舊知遷移,在生長點回顧
在教學中,教師要全面把握知識體系的整體結構,結合學生的已有認知,尋找知識的生長點,帶領學生及時回顧,關聯(lián)舊有的知識,通過遷移轉化,找到促進新舊知識之間的融合,從而提升學生的數(shù)學思維。
比如,在教學“乘法分配律”這一內(nèi)容時,我發(fā)現(xiàn),學生實際上早就運用過乘法分配律,只是當時運用的時候并不知道。這正好是一個“回頭看,溫故而知新”的好機會,能夠幫助學生深入理解乘法分配律。我讓學生回顧之前的乘法口算25×3,說說之前口算的方法,學生認為之前的口算就是將25分成20+5,這樣就是20×3=60,5×3=15,再將 60+15=75;我又出示筆算題 25×12,讓學生說說是怎么筆算的,并說出算理。學生梳理了筆算的算理,由此對算理有了深刻的理解,認識到之前學過的算理其實也是乘法分配律的算理。
在以上環(huán)節(jié)中,教師基于學生舊知的層次,借助對舊有知識的回顧,帶領學生復習了之前口算和筆算的算理,同時也對乘法分配律的理論支撐有了更深刻的認識,由此,讓學生的數(shù)學思維得到了重組和建構。
二、基于新知整合,在延伸點眺望
在實踐中,很多知識之間存在著緊密的關聯(lián),教師可在把握整體知識脈絡的基礎上,根據(jù)學生的基本學情,結合知識體系當中的上下關聯(lián),進行延伸和拓展,引導學生適度眺望。
比如,在教學“一位小數(shù)的認識”這一內(nèi)容之后,學生已經(jīng)深入理解了一位小數(shù)的意義,并能夠熟練讀寫一位小數(shù),對一位小數(shù)與分數(shù)十分之幾的關系有了把握,此時,我引導學生思考:“華華身高1米5厘米,軍軍身高1.1米,你知道誰更高嗎?”學生很快指出,將軍軍身高1.1米換算成1米10分米,華華的身高1米5厘米換算成1米50分米,這樣就知道華華的身高更高了,我追問:“如果用米做單位,1米5厘米、1米7厘米,可以怎么表示?”學生提出用小數(shù)來表示,此時我再追問:“是1.5 米、1.7 米嗎?為什么?”學生發(fā)現(xiàn),厘米和米之間的換算單位不是一位數(shù),而是兩位數(shù),因此不能用一位小數(shù)表示,可是到底如何表示呢?學生充滿了疑問,產(chǎn)生了新知學習的需求,為下一步繼續(xù)探討兩位小數(shù)埋下了伏筆。
以上環(huán)節(jié),教師在學生熟練掌握一位小數(shù)的知識之后,并沒有止步,而是向前適當眺望,不但激活了學生的原有認知,而且激發(fā)了學生探索新知的欲望,提升了學生探索的興趣。
三、基于核心錯誤,在易混點質疑
在小學數(shù)學教學中,概念、法則、公式等屬于基礎知識,是數(shù)學教學的核心所在。為此,教師要基于學生的核心錯誤,引導學生比較、辨析,從而提高數(shù)學課堂教學的實效性。
比如,在教學“三角形的分類”這一內(nèi)容時,學生對直角三角形、銳角三角形、鈍角三角形的認識容易陷入膚淺的表象層次,為此,我出示圖1~3,讓學生判斷是什么三角形。學生很快判斷出圖1是直角三角形,圖2是鈍角三角形,但到了圖3時,學生依然快速判斷為銳角三角形,此時我質疑:“真的是銳角三角形嗎?請舉例說明。”學生舉例一個銳角三角形中的銳角;我繼續(xù)質疑:“那鈍角三角形難道沒有銳角嗎?”于是,學生猜這個三角形是鈍角三角形,我仍然質疑:”那直角三角形難道沒有銳角嗎?”學生于是猜這是個直角三角形。接下來,我繼續(xù)質疑:“為什么有一個角是直角的三角形就是直角三角形,有一個角是鈍角的三角形是鈍角三角形,而有一個銳角的三角形就不是銳角三角形?”
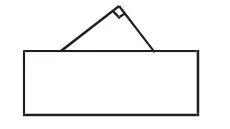
圖1
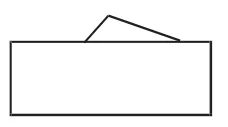
圖2

圖3
以上環(huán)節(jié),教師基于學生的錯誤,通過質疑,帶領學生在容易混淆的知識點處強化認知,讓學生認識到,根據(jù)露出的一個銳角,并不確定三角形就是銳角三角形,因為鈍角三角形和直角三角形中都有銳角。由此,學生也對銳角三角形的特點“三個角都是銳角三角形”有了深刻的理解,建構了新的數(shù)學概念。
總之,學生思維的發(fā)展,需要在已有認知的基礎上進行重組和改造,教師要基于學生已有新舊知識,把握知識的生長點、延伸點、易混點三個思維接口,新舊融合,去偽存真,才能實現(xiàn)課堂教學的有效性。

