Threshold characteristics of short-pulsed loads combined with the ultrasound field causing dynamic delamination of adhesive joints

Nikoli Gorbushin, Yuri Petrov,*, Y-Pu Zho, Yin Zhng

aSt.-Petersburg State University, St.-Petersburg 198504, Russia

bInstitute of Problems of Mechanical Engineering, St.-Petersburg 199178, Russia

cState Key Laboratory of Nonlinear Mechanics (LNM), Institute of Mechanics, Chinese Academy of Sciences, Beijing 100080, China

dSchool of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China

Rapidly emerging areas of engineering that operate at small scales gave rise to many various problems for modelling. One of them is related to the behaviour of a solid structure at microlevel subjected to adhesive forces. These problems are essential for consideration, for instance, in microelectromechanical systems (MEMS) when structures lose their capacity by stiction of their parts to a substrate [1, 2], or while developing the adhesives that may mimic the sticking mechanism that geckos use [3, 4].

There is a standard procedure of measuring an adhesive strength which is referred to as the peeling test [5]. The measurements are performed under quasi-statical loading conditions and allow to obtain a work of adhesion as an output parameter in a simple way. Although this test is tabulated and gives useful results, the consideration of inertia effects may deliver alternative ways in coping with the problems.

In such a way, it was shown that the application of a background vibrational field can substantially decrease the load that causes the failure of adhesive bonds [6, 7]. In this paper, we analyse the effect of background vibrational load on the adhesive failure in a simple model of a finite string on an elastic foundation. The model can be easily adopted for the beam structures that are usually studied for MEMS [1, 2, 5, 7, 8]. The main point of this work is to demonstrate the modelling approach and the physical effects with the help of the structural–temporal fracture criterion, also known as the incubation time criterion [9-11]. The choice of this criterion is reasoned by the fact that it can capture features of dynamical processes in fracture [10-12], structural changes of media [13, 14], etc.

We consider a string of lengthLattached to an elastic foundation characterised by constantk. The tension of the string isμand a unit length density isρ. Figure 1 displays the configuration of the problem in question. The vertical displacement of a string isu=u(x,t). The governing equation in the range 0 ＜x＜L,t＞ 0 for the considered setting is

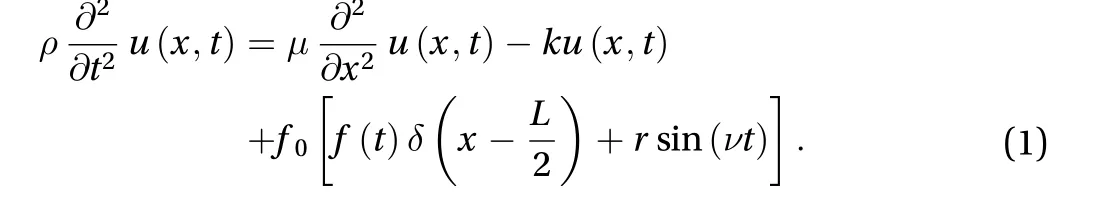
The last equation is usually used for illustration of dispersive waves and can be derived similarly to Ref. [15]. We prescribe homogeneous initial conditions and boundary conditions corresponding to the clamped ends

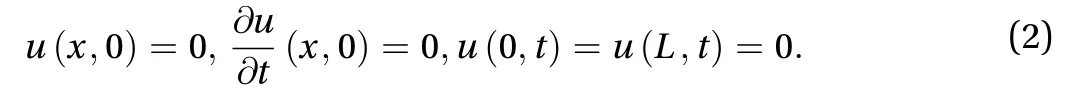
External load is considered as a concentrated force at the centre of a string, highlighted by the Dirac delta functionδ(x) in Eq. (1),with time variable valuef0f(t), wheref0characterises the amplitude of the force whilef(t) is a dimensionless pulse of the force, which is specified below. There is also a background vibrational load,rf0sin(νt), whose amplitude is a fraction of a concentrated force, given by ratior. The excitation frequency of external force is given byν.

It should be noticed that the foundation can behave differently in tension and compression, which indeed happens in practice. Thus, for this case the stiffness of the foundation should be chosen to be dependent on the displacement of a string.However, the mathematical formulation of the problem will becomes significantly more complicated in derivation of the solution. As long as we are concerned in demonstration of fracture event, we chose the simplest case.

We suppose that fracture happens in the middle part of the string, right at the spot where the concentrated force is located.This assumption appears to be reasonable as long as the concentrated forcef0f(t) generate the elongation of the spring. The investigation of different amplitudesf0of this force allows to determine the critical values depending on the various pulse functionsf(t). The question that is addressed in this work is: how does the vibrational field effect the critical amplitude of concentrated force?

To answer the posed question we, firstly, need to obtain the solution of the problem presented in Eq. (1). The solution can be obtained by means of separation of variables. We use the final expression foru(x,t) that can be found in Ref. [16] for a general type of loadg(x,t)

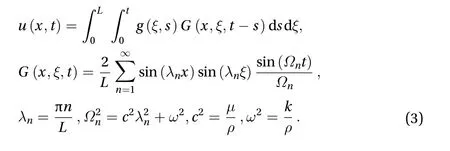
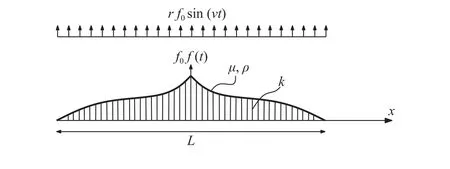
Fig. 1. String of length L, density ρ, and tension μ attached to an elastic foundation with stiffness k. The string subjected to a load at its centre f0f(t) and simultaneously to background harmonic vibrations rf0sin(νt).

Thus, in order to obtain the results we need to specify the concentrated load and perform the integration. We consider three major types of pulsesf(t)=fj(t),j=1, 2, 3, where

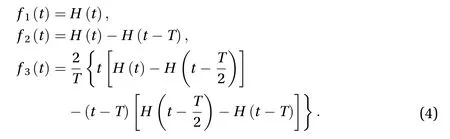
The first type of pulsef1(t) is just a constant load of unit amplitude over the whole period of time while the second onef2(t) is a step pulse of durationTand unit magnitude. The last of the considered cases gives a symmetrical triangular pulse of durationTand, again, unit amplitude.

Hence, the solution of the problem in mind in the middle of the string,x=L/2, can be presented as

Each solutionujreflects the choice of the load in Eq. (4) forj= 1,2, 3, respectively. The coefficientsAn(j)are defined as

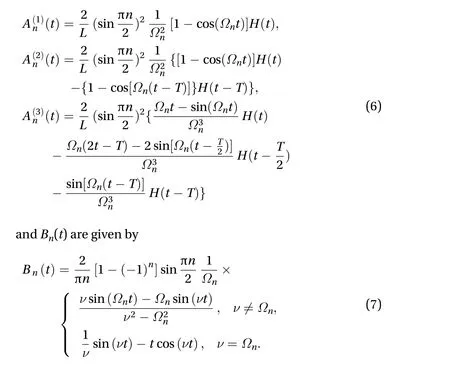
The achieved solution allows to find the critical value of loading amplitudef0that is required to cause the fracture of a spring in the middle of the structure. The prediction of this event can be based on the appropriate fracture condition. In this work we choose it to be of a following kind:

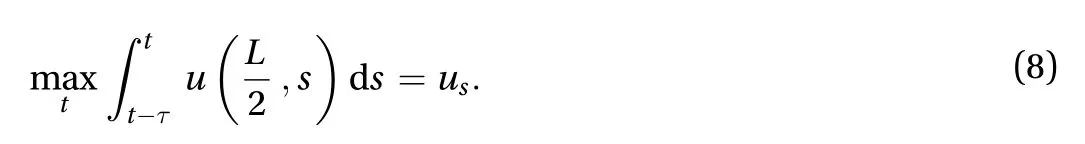
Valueuscorresponds to the linear elongation of a spring under quasi-static loading condition. This value can be easily determined experimentally. The other quantity in fracture condition Eq. (8) is incubation timeτ. This time characterises the rapidity of the fracture events and allows to model failure events at high-strain rates. This parameter is considered as a material property and can be measured by the experiments as well [17,18].

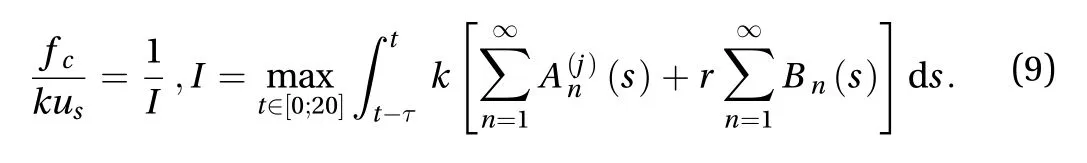
Utilising obtained expressions for the solution in Eq. (5) and also fracture condition Eq. (8) we write down the equation for a critical loading amplitude In the last expressionkusis the force that breaks a spring if loaded quasi-statically. Ranget∈[0, 20] was chosen just to illustrate the used criterion. It was required in order to make possible to observe the fracture in finite time, otherwise the fracture event happens in infinite time.

To evaluate the dependence in Eq. (9) one has to set the model parameters. For the illustrative purposes, we define their values in appropriate physical units as:L= 1[L],ρ= 1[M],μ=10[F],k= 5[F/L2]. The incubation time is taken in time unitsτ=0.1[T]. The effect of introduced external vibrations is demonstrated in Fig. 2 in the case of constant load with time,f1(t), from Eq. (4). As one can see, the adopted incubation time criterion Eq.(8) reveals a decrease in critical forces close to the eigenfrequencies in comparison with a case without introduced vibrations (r= 0). This effect is significant for optimisation of detachment processes as it gives an opportunity to cause a fracture with less efforts. Even for the small amplitudes of vibrational fields,r= 0.1, there is a noticeable reduction of critical amplitudes. For higher amplitudes, for exampler= 0.5, the effect is event more pronounced. This observation is caused by the resonance which is provided by the background vibration, which is underlined by Eq. (7). Notice that such effect is presented for the odd eigenfrequencies which follows from the chosen boundary conditions.The alternative choice of boundary conditions will result in the drop of amplitude at points different from those presented in Fig. 2.

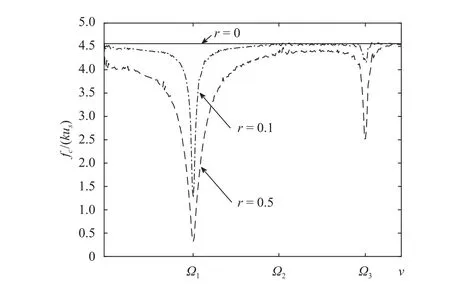
Fig. 2. Effect of background vibrational field on critical load in case f1(t).

A lot of phenomena in dynamic fracture mechanics appear at short pulses of load. In Fig. 3 one can observe that for two different shapes of pulses without an external vibration, the critical force infinitely grows when the duration of the pulse decreases.At the same time the critical force for a triangular pulse appears to be greater than in the case of step pulsef2(t).

Introduction of external vibrations allows to drop the values of critical load. Notice that this happens even not at the resonant frequency. Interestingly, with the growth of pulse duration the critical force tends to a constant value. This value is recovered if the conventional criterion, i.e.,τ→ 0, is considered. So to say, the curves in Fig. 3 distinguish the fracture processes between high rate processes and low rate ones. Moreover, the decrease of duration pulse to 0 results in the fracture caused by a vibrational field only. Furthermore, there is a tendency in decrease offcwith the increase ofr. The introduction of incubation time criterion Eq. (8) allows to capture rate dependence of fracture processes, according to its original purpose and definition[9, 10], avoiding to impose the rate-dependence of the other material properties responsible for fracture.

To summarise, the simplified adhesion problem was analysed. We considered the failure of adhesion in the model of a string on the elastic foundation. The main aim of the study was to examine the influence of a background vibrations on the integrity of the structure under some principal load. It was shown that, imposing a background vibration on the already applied load, it is possible to considerably decrease the value of the critical force. At the same time, in the case of a pulse load, it was demonstrated that the critical load is characterised by the dynamic and static branches, which depend on the relation between the time characteristics of the basic and background effects and also on the parameters of the system. The obtained results show the possibility of controlling the detachment by imposing a proper vibrational load. The experimental validation of the examined problem is still needed. However, the wide range of applicability of the incubation time criterion in similar cases [9,11, 13] provides the support for the achieved results in the present paper and expectation of their correctness.

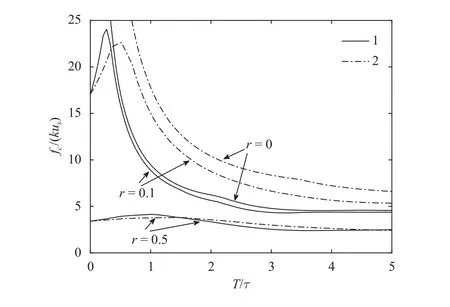
Fig. 3. Effect of background vibrational field on critical load in cases f2(t) and f3(t) given by curves 1 and 2, respectively. The excitation frequency is ν = 0.9Ω1.

Acknowledgement

This work was supported by the Russian Foundation for Basic Research (16-51-53077) and the National Natural Science Foundation of China (11611130019).

[1]N. Tas, T. Sonnenberg, H. Jansen, et al., Stiction in surface micromachining, J. Micromech. Microeng. 6 (1996) 385–397.

[2]Y.-P. Zhao, L. Wang, T. Yu, Mechanics of adhesion in memsa review, J. Adhes. Sci. Technol. 17 (2003) 519–546.

[3]H. Lee, B.P. Lee, P.B. Messersmith, A reversible wet/dry adhesive inspired by mussels and geckos, Nature 448 (2007) 338–341.

[4]Y. Zhao, T. Tong, L. Delzeit, et al., Interfacial energy and strength of multiwalledcarbon-nanotube-based dry adhesive, J.Vac. Sci. Technol. B 24 (2006) 331–335.

[5]C. Mastrangelo, C. Hsu, A simple experimental technique for the measurement of the work of adhesion of microstructures,in: Solid-State Sensor and Actuator Workshop, 1992. The 5th Technical Digest., IEEE, 1992, pp. 208-212.

[6]N. Gorbushin, Y.V. Petrov, Effect of combined high-frequency and pulsedynamic impact on adhesive-joint strength, Doklady Physics 61 (2016) 384-388.

[7]A.A. Savkar, K.D. Murphy, Z.C. Leseman, et al., On the use of structural vibrations to release stiction failed MEMS, J. Microelectromech. Syst. 16 (2007) 163–173.

[8]Y. Zhang, Y.-P. Zhao, Determining both adhesion energy and residual stress by measuring the stiction shape of a microbeam,Microsyst. Technol. 21 (2015) 919–929.

[9]Y.V. Petrov, A. Utkin, Dependence of the dynamic strength on loading rate, Mater. Sci. 25 (1989) 153–156.

[10]Y.V. Petrov, N. Morozov, On the modeling of fracture of brittle solids, J. Appl. Mech. 61 (1994) 710–712.

[11]Y.V. Petrov, Incubation time criterion and the pulsed strength of continua: fracture, cavitation, and electrical breakdown,Doklady Physics 49 (2004) 246-249.

[12]Y.V. Petrov, N. Morozov, V. Smirnov, Structural macromechanics approach in dynamics of fracture, Fatigue Fract. Eng. Mater.Struct. 26 (2003) 363–372.

[13]Y.V. Petrov, E.V. Sitnikova, Dynamic cracking resistance of structural materials predicted from impact fracture of an aircraft alloy, Tech. Phys. 49 (2004) 57–60.

[14]G. Volkov, V. Bratov, A. Gruzdkov, et al., Energy-based analysis of ultrasonically assisted turning, Shock Vib. 18 (2011) 333–341.

[15]K.F. Graff, Wave Motion in Elastic Solids, Courier Corporation,2012.

[16]A. Polyanin, V. Nazaikinskii, Handbook of Linear Partial Differential Equations for Engineers and Scientists, CRC Press, 2015.

[17]S. Krivosheev, Y. Petrov, Testing of dynamic property of materials under microsecond duration pressure created by the pulse current generator, in: Proceedings of International Conference on Megaggauss Magnetic Field Generation and Related Topics.Moscow-St. Petersburg, 2002, pp. 112-115.

[18]S. Krivosheev, Pulsed magnetic technique of material testing under impulsive loading, Tech. Phys. 50 (2005) 334–340.