基于雙光楔的雙模光學系統設計分析

李福巍 張運強 潘國慶

摘 要：????? 在導引系統中， 將雙光楔結構與雙模復合光學系統相結合， 使復合光學系統保持不動， 通過雙光楔的運動來實現系統的掃描和跟蹤。 這種設計不僅簡化了位標器的設計， 也給復合光學系統的設計提供了足夠空間余量， 有利于導引系統的總體設計。 本文提出一種基于雙光楔的紅外/激光雙模光學系統設計方案， 可用于獲取目標的雙模信息， 分析了光學系統的基本參數， 研究了采用雙光楔結構對掃描視場的實現方法， 并對整體光學系統進行了設計。 所設計系統實現了紅外和激光雙波段的良好成像， 滿足導引系統的使用需求。

關鍵詞：???? 光學設計; 雙模光學系統; 雙光楔

中圖分類號：??? TN219; TN249 文獻標識碼：??? A文章編號：???? 1673-5048（2018）01-0043-04

0 引? 言

在現代化空天戰爭中， 精確制導武器成為實施毀滅性打擊的重要手段。 目前， 精確制導武器導引制導方式主要包括紅外制導、 激光制導、 雷達制導等。? 隨著未來戰爭環境越來越復雜， 攻防對抗越來越激烈， 精確制導武器的打擊能力受到嚴重的影響， 多模復合制導方式得到了快速的發展， 這種方式不僅提高了抗干擾能力和復雜戰場環境下的命中精度， 同時具備打擊多種目標的能力， 提高武器作戰靈活性和作戰效能[1]。

目前， 多模復合制導技術中最常見的是雙模制導技術， 在導彈上應用和正在發展的雙模制導技術主要包括雷達/紅外、 雷達/電視、 紫外/紅外、 可見光/紅外、 毫米波/紅外和紅外/激光等。 其中紅外成像/激光成像復合制導技術是該領域的一個重要分支[2]。

然而， 由于兩種制導方式的復合必然會增加光學系統的體積和重量， 從而增加導引系統位標器的設計難度， 特別是對位標器的空間布局和響應速度有很大的影響。 因此， 本文考慮將雙光楔結構與雙模復合光學系統相結合， 使復合光學系統保持不動， 通過雙光楔的運動來實現系統的掃描和跟蹤。 這種設計簡化了位標器的設計， 并給復合光學系統的設計提供了足夠空間余量， 更有利于系統的總體設計。

1 雙模復合光學系統參數確定

1.1 系統設計思路

目前較為常用的位標器結構有雙框架式和橫滾俯仰兩軸式等， 光學系統一般要安置在某個框架上， 隨框架進行運動， 達到對目標搜索和跟蹤的目的。

然而， 這樣的結構對光學系統的重量和尺寸有較為嚴格的要求， 限制了光學系統的設計， 特別是雙模光學系統， 由于要將兩個波段融合在一起，

必然要增加體積和重量， 影響位標器的跟蹤速度和響應能力等， 從而給位標器設

計帶來壓力。

因此， 本文利用光楔對光線的偏折特性， 通過雙光楔旋轉實現系統的掃描和跟蹤， 僅采用兩個轉動機構， 負載兩個光楔進行運動， 極大地簡化了位標器的設計; 同時， 這樣設計使后面的光學系統與彈體固定在一起即可， 不需要隨運動機構進行運動，? 從而不需要對光學系統進行嚴格的尺寸和重量控制， 為其提供了較大的設計裕度， 有利于性能的提高。

1.2 系統性能指標

1.2.1 紅外分系統技術指標

（1） 紅外接收系統視場： 5°×4°。

（2） 中波致冷面陣探測器， 像元中心距： 30? μm×30 μm;? 像元數： 320×256。

（3） 工作波段： 3～5? μm。

1.2.2 激光分系統技術指標

（1） 激光接收系統視場： 2°×1.6°。

（2） 近紅外探測器，? 像元中心距： 30 μm×30 μm; 像元數： 320×256。

（3） 工作波段： 1.57 μm。

1.3 光學參數計算

1.3.1 焦距

焦距計算公式如下：

f ′=d2tanω（1）

式中： ω為半瞬時視場角; d為探測器光敏面尺寸; f ′為光學系統焦距。

計算可得紅外接收光學系統焦距為

f ′IR=320×30 μm2tan（5°/2）=109.9 mm

計算可得激光接收光學系統焦距為

f ′Laser=320×30 μm2tan（2°/2）=275 mm

1.3.2 系統入瞳口徑

入瞳口徑計算公式如下：

DIR=f ′F/#（2）

式中： F/#為系統F數。

紅外接收系統F/#由制冷探測器本身決定， 則計算可得紅外接收系統入瞳口徑為

DIR=f ′F/#=109.9 mm1.88=58.5 mm

激光接收系統入瞳口徑與紅外接收系統保持一致， 設計時也將其確定為58.5 mm。

2 雙光楔參數確定

2.1 光楔偏折原理

光楔是楔角α很小的棱鏡， 由于折射角很小， 其偏向角δ公式可以大大簡化， 如公式（3）所示：

δ=α（n-1）（3）

2.2 光楔對消色差原理

由于光楔和棱鏡都具有色散的特性， 因此， 當發生偏折時要考慮系統的色差， 對于該問題可以采用組合光楔對減小色差的影響[3]。 組合光楔對是由兩個不同材料的光楔組成一個光楔對， 楔角大的光楔采用色散小的硅材料， 楔角小的光楔采用色散大的鍺材料。 根據公式（4）～（5）建立色散方程：

αGe（nGe-1）+αSi（nSi-1）=β（4）

αGe（nGe-1）VGe+αSi（nSi-1）VSi=0（5）

式中： n為不同材料的折射率; α為光楔的楔角; V為不同材料的阿貝數; β為光束的偏折角度。

本文系統要求掃描范圍為±50°， 即要求單光楔對的偏折角度為25°， 利用以上公式可以計算得到： αGe=1.3°， αSi= 12.5°， 確定光楔對如圖1所示。

2.3 雙光楔對結構確定

根據上文對光楔材料的選擇和角度的設計， 確定雙光楔對結構， 見圖2。 圖中位置為偏轉角度最大時， 兩組光楔對的情況。

根據資料上提到的矢量法， 利用公式（6）計算雙光楔對相對運動時光線的偏轉情況[4-8]：

φ=2δcos（（θ2-θ1）/2） （6）

式中： φ為總偏轉角;?? θ1為光楔對1的轉動角度;? θ2為光楔對2的轉動角度。

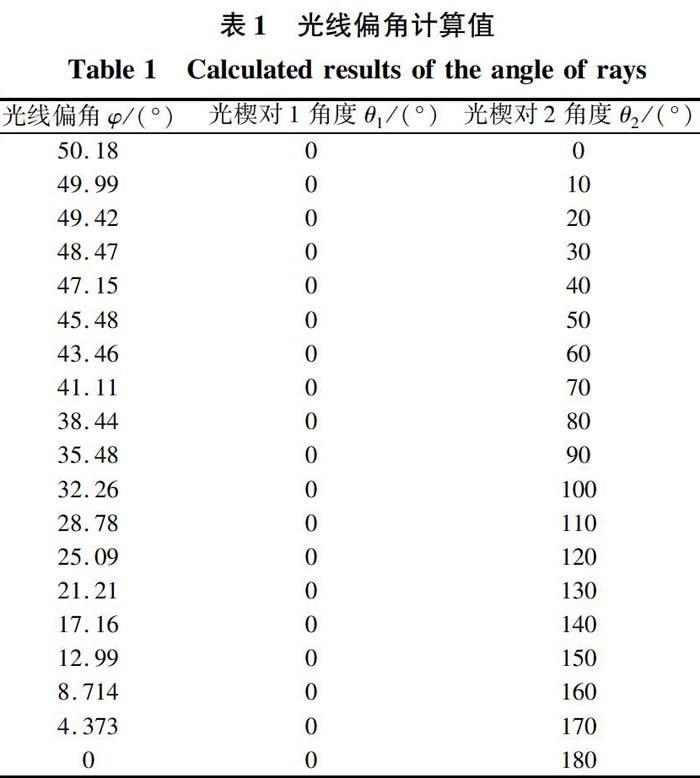
假設光楔對1不動， 光楔對2旋轉180°， 以10°為間隔進行計算， 表1為計算得到的光線偏角。

通過光學軟件進行光線追跡， 可以得到實際最大偏移量為51°， 達到指標的要求。 圖3為光線最大偏向角的情況。 圖4為光線最小偏向角的情況， 即無偏向， 僅有一個向下的位移。

3 系統復合設計

3.1 系統結構選擇

通過對各種結構形式光學系統的分析， 確定使用透射式結構， 采用一個半反半透的分光鏡將兩個波段分開， 使光線入射到兩個不同的探測器上。

由于系統的搜索視場是由雙光楔保證的， 因此， 給光學系統的設計帶來了更大的裕度。 不需要嚴格控制光學系統的長度和重量等， 為系統的優化設計提供了方便。

3.2 設計結果

根據以上設計思想， 利用光學設計軟件優化后得到的光學系統如圖5所示。

4 設計結果分析

復合光學系統傳遞函數（MTF）曲線如圖6～7所示。 圖中不同的曲線表明了不同視場的MTF， 實線為子午方向， 虛線為弧矢方向。 圖6為紅外分系

統的傳遞函數， 由于色差的影響曲線距離衍射極限有一定的距離， 但是已經可以滿足系統的使用要求。 圖7為激光分系統的傳遞函數， 由于激光為單色光， 沒有色差的影響， 其成像質量很好， 已經可接近衍射極限。

5 結? 論

本文對基于雙光楔的紅外/激光雙模光學系統設計方法進行了研究， 并設計得到一套可以對紅外中波波段和激光波段成像的系統。 該系統以雙光楔為掃描機構， 簡化了導引系統位標器的設計， 并為光學系統提供了足夠的設計余量， 保證了光學系統獲得良好的成像質量。 該系統可以滿足紅外/激光復合成像制導導引系統的使用要求， 為今后該方向的研制工作奠定良好的基礎。

參考文獻：

[1] 劉代軍， 張蓬蓬. 美國下一代空空導彈發展歷程與啟示[J]. 航空兵器， 2016（2）： 3-8.

Liu Daijun， Zhang Pengpeng. Development and Revelation of US Next Generation Air-to-Air Missile[J]. Aero Weaponry， 2016（2）： 3-8. （in Chinese）

[2] 李福巍， 張運強， 潘國慶. 紅外/激光雙模共口徑光學系統設計[J]. 應用光學， 2012， 33（3）： 496-499.

Li Fuwei， Zhang Yunqiang， Pan Guoqing. Optical Design of IR/Laser Dual-Mode Common Aperture System[J]. Journal of Applied Optics， 2012， 33（3）： 496-499.（in Chinese）

[3] 張以謨. 應用光學[M]. 3版. 北京：電子工業出版社， 2008.

Zhang Yimo. Optical Application[M]. 3rd ed. Beijing： Publishing House of Electronics Industry， 2008.（in Chinese ）

[4] 郭云曾， 楊小軍， 楊小君， 等. 旋轉雙光楔光路引導系統Matlab仿真研究[J]. 紅外與激光工程， 2014， 43（3）： 856-860.

Guo Yunzeng， Yang Xiaojun， Yang Xiaojun， et al. Simulation Study of Rotating Double Optical Wedge Vectoring Optics Path Based on Matlab[J]. Infrared and Laser Engineering， 2014， 43（3）： 856-860.（in Chinese）

[5] 虞林瑤， 魏群， 張天翼， 等. 無熱化旋轉雙光楔共形光學系統設計[J]. 紅外與激光工程， 2014， 43（2）： 528-534.

Yu Linyao， Wei Qun， Zhang Tianyi， et al. Design of A Thermal Conformal Optical System Based on Rotated Phase Plates[J]. Infrared and Laser Engineering， 2014， 43（2）： 528-534.（in Chinese）

[6] Florea C，? Sanghera J S，? Aggarwal I D. Broadband Beam Steering Using Chalcogenide-Based Risley Prisms[J]. Optical Engineering， 2011， 50（3）： 033001.

[7] Li Anhu， Jiang Xuchun， Sun Jianfeng， et al. Radial Support Analysis for Large-Aperture Rotating Wedge Prism[J]. Optics & Laser Technology， 2012， 44（6）： 1881–1888.

[8] 趙軍麗， 吳易明， 高立民， 等. 旋轉雙光楔系統用于像移補償的技術研究[J]. 紅外與激光工程， 2015， 44（5）： 1506-1511.

Zhao Junli， Wu Yiming， Gao Limin， et al. Technology Research on Image Motion Compensation of the Rotating Double Optical Wedge [J]. Infrared and Laser Engineering， 2015， 44（5）： 1506-1511.（in Chinese）