BCK-代數的廣義 (∈,∈∨q)-模糊蘊涵理想*
彭家寅
內江師范學院 數學與信息科學學院,四川 內江 641199
1 引言
人工智能的一個重要任務就是使計算機模擬人腦去處理確定的與不確定的信息。邏輯的形式化推理在演繹證明中突顯強勁的優勢。邏輯規則在計算機科學和數學中既是應用的工具,又是奠定理論基礎的技術手段。特別地,非經典邏輯已成為計算機科學處理模糊信息與不確定信息的有力工具。BCK-代數類是一種重要的模糊邏輯代數類[1],它被Imai和Iseki[2-3]提出,隨后得到了許多學者的深入研究[4-6]。其中Iseki和Tanaka引入了BCK-代數的理想的概念,并討論了它的性質[4];Meng[6]引入了BCK-代數的蘊涵理想的概念,并研究了它與正蘊涵理想、交換理想之間的關系。
1965年,Zadeh[7]提出了模糊集的概念,成為描述現實世界中不確定問題的一種方法。至今,模糊集理論被廣泛地應用于許多數學分支中,如群、函數論、概率論、拓撲學等。1991年,Xi[8]將模糊集用于BCK-代數中。此后Meng和Guo[9]引入了BCK/BCI-代數的模糊理想的概念。Jun和Roh等人[10-11]提出了BCK-代數的模糊交換理想和模糊正蘊涵理想的概念并研究了它們的性質。Peng[12]和Meng等人[13]分別研究了BCK-代數的不分明化蘊涵理想和模糊蘊涵理想。自Pu和Liu[14]于1980年引入了模糊點與模糊集的屬于與重于關系后,Zhang等人[15]將Pu與Liu的思想應用于BCK/BCI-代數結構的討論中,提出了BCK/BCI-代數的(∈,∈∨q)模糊理想的概念。Liu和Xin[16]引入BCK-代數的 (∈,∈∨q)-模糊蘊涵理想。Liu[17]討論BCK-代數的(∈,∈∨q)-模糊理想的一般形式,提出了 (∈,∈∨qδ)-模糊理想的概念。此外,他還將軟集用于BCK/BCI-代數中,引入了 (∈,∈∨q)-模糊軟理想的概念并研究其性質[18]。本文在文獻[17]的基礎上,將文獻[16]中BCK-代數的 (∈,∈∨q)-模糊蘊涵理想進行推廣,引入BCK-代數的 (∈,∈∨qk)-模糊蘊涵理想的概念,并討論其性質,研究它與(∈,∈∨qk)-模糊理想間的關系,探究(∈,∈∨qk)-模糊蘊涵理想的等價刻畫,研究基于蘊涵的BCK-代數之模糊蘊涵理想。
2 預備知識
一個(2,0)型代數(X;?,0)叫作BCK-代數,如果它滿足對任意x,y,z∈X,有:

在BCK-代數中定義自然序“≤”:x≤y當且僅當x?y=0。這樣(X;≤)便是一個以0為最小元的偏序集,且對任一BCK-代數X及任意x,y,z∈X,下列結論成立:

BCK-代數X的一個非空子集I叫作X的一個理想,如果滿足(i)0∈I,(ii)x?y∈I且y∈I蘊涵x∈I。BCK-代數X的非空子集I稱為X的一個蘊涵理想,如果它滿足(i)和(iii)x∈I當 (x?(y?x))?z∈I且z∈I;稱它為交換理想,如果它滿(i)和(iv)x?(y?(y?x))∈I當(x?y)?z∈I且z∈I;稱它為正蘊涵理想,如果它滿足(i)和(v)x?z∈I僅當(x?y)?z∈I且y?z∈I。
定義1X的模糊子集μ是指映射μ:X→[0,1],并稱U(μ;t)={x∈X|μ(x)≥t}為模糊集μ的t-水平集。
定義2BCK-代數X的模糊子集μ叫作X的一個模糊理想,如果它滿足x,y∈X,有:

定義3BCK-代數X的一個模糊子集μ叫作X的一個模糊蘊涵理想,如果它滿足(F1)且x,y,z∈X,有:
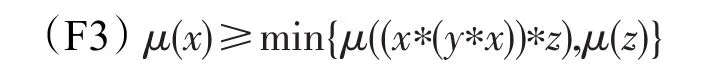
定義4模糊集μ:
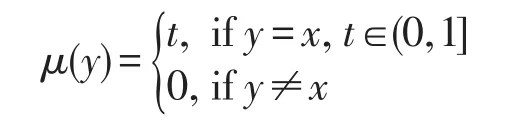
叫作以x為支點、值為t的模糊點,并記為xt。
對于模糊點xt與模糊集μ,Pu和Liu[14]引入符號xtα μ,其中α∈{∈,q,∈∨q,∈∧q}。說模糊點xt屬于(重于)模糊集μ,記為xt∈μ(xtqμ),如果μ(x)≥t(μ(x)+t>1)。如果xt∈μ或xtqμ,則記為xt∈∨qμ,而符號意味著∈∨q不成立。
定義5[17]BCK-代數X的模糊子集μ叫作X的(∈,∈∨qk)-的模糊理想,如果它滿足:
(I-1)對任意x∈X和t∈(0,1],xt∈μ蘊涵0t∈∨qkμ。
(I-2)對任意x,y∈X和t,r∈ (0,1],(x?y)t∈μ與yr∈μ蘊涵xmin{t,r}∈∨qkμ。
3 BCK-代數的廣義 (∈,∈∨q)-模糊蘊涵理想
定義6設除特殊聲明外,文中X總是表示一個BCK-代數,而且k表示[0,1]任意一個實數。符號xtqkμ是指μ(x)+t+k>1;xt∈∨qkμ意味著xt∈μ或xtqkμ。對于意味著xtα μ不成立。
定義7BCK-代數X的模糊子集μ叫作X的(∈,∈∨qk)-模糊蘊涵理想,如果它滿足:
(I1)對任意x∈X和t∈(0,1],xt∈μ蘊涵 0t∈∨qkμ。
(I2)對任意x,y,z∈X和t,r∈(0,1],zr∈μ與 ((x?(y?x))?z)t∈μ蘊涵xmin{t,r}∈∨qkμ。
當k=0時,X的一個(∈,∈∨qk)-模糊蘊涵理想就是X的(∈,∈∨q)-模糊蘊涵理想。
例1設X={0,1,2,3,4}為一個BCK-代數,其中Cayley表如表1。

Table 1 “?”operator table inX表1 X中的“?”運算表
定義X上的模糊子集μ為μ(0)=0.5,μ(1)=μ(2)=0.35且μ(3)=μ(4)=0.7。容易驗證,μ是X的一個(∈,∈∨q0.4)-模糊蘊涵理想。但它既不是X的模糊蘊涵理想,也不是(∈,∈∨q)-模糊蘊涵理想,因為μ(0)=0 0.5<0.7=μ(2),40.7∈μ并且 ((1?(2?1))?4)0.5∈μ,可是定理1設μ為BCK-代數X的模糊子集,則下列結論成立:
(1)每個模糊蘊涵理想都是 (∈,∈∨qk)-模糊蘊涵理想。
(2)每個 (∈,∈∨q)-模糊蘊涵理想都是 (∈,∈∨qk)-模糊蘊涵理想。
證明(1)設μ是X的一個模糊蘊涵理想。一方面,令x∈X且t∈(0,1]使得xt∈μ,則μ(x)≥t。結合(F1)有μ(0)≥μ(x)≥t,因此 0t∈μ,進而 0t∈∨qkμ。另一方面,設x,y,z∈X且t,r∈(0,1],使得 ((x?(y?x))?z)t∈μ且zr∈μ,則μ((x?(y?x))?z)≥t且μ(z)≥r。由(F3)可得μ(x)≥min{μ((x?(y?x))?z),μ(z)}≥ min{t,r},故xmin{t,r}∈μ,于是xmin{t,r}∈∨qkμ。綜上所述μ是X的一個(∈,∈∨qk)-模糊蘊涵理想。
(2)假設μ是X的一個 (∈,∈∨q)-模糊蘊涵理想,則①對任意x∈X和t∈(0,1],xt∈μ蘊涵0t∈ ∨q μ;②對任意x,y,z∈X且t,r∈(0,1],((x?(y?x))?z)t∈μ并且zr∈μ蘊涵xmin{t,r}∈∨q μ。現考慮①:如果 0t∈μ,則0t∈∨qkμ;如果 0tq μ,那么μ(0)+t>1,因此μ(0)+t+k>1,這表明 0t∈∨qkμ,即條件①蘊涵條件(I1)。類似地,可得條件②蘊涵條件(I2),故(2)為真。□
定理2BCK-代數X的模糊子集μ是X的(∈,∈∨qk)-模糊蘊涵理想的充分必要條件是對任意x,y,z∈X,有:
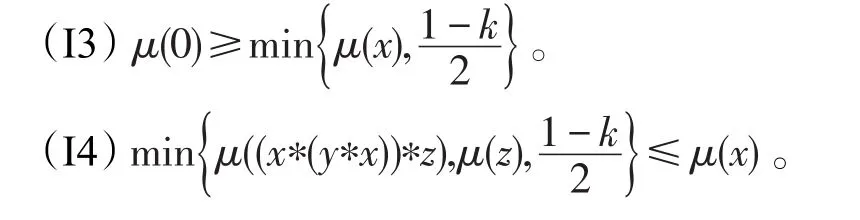
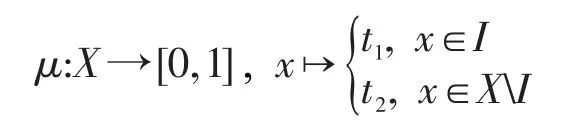
證明假設μ是X的一個(∈,∈∨qk)-模糊蘊涵理想。如果(I3)不成立,則存在a∈X使得μ(0)<當有μ(0)<μ(a),進而存在使得μ(0) 假設(I4)不成立,則存在a,b,c∈X使得μ(a)<如果 min{μ((a?(b?a))?c),那么存在使得 min{μ((a?(b?因此 ((a?(b?a))?c)t∈μ且cr∈μ。但因且μ(a)+min{t,r}<2t<1-k,有且,即它與(I2)矛盾。如果那么且因此且故這與(I2)矛盾,因此(I4)成立。 反之,設μ是X的一個模糊子集且滿足(I3)和(I4)。令t∈(0,1]使得xt∈μ,那么μ(x)≥t。結合(I3)有: 條件μ(0)≥t蘊涵 0t∈μ。由可得μ(0)+t>即 0tqkμ。因此 0t∈∨qkμ,故(I1)成立。 假定x,y,z∈X且t,r∈(0,1]使得 ((x?(y?x))?z)t∈μ且zr∈μ,則μ(z)≥r并且μ((x?(y?x))?z)≥t。結合(I4)有: 條件μ(x)≥min{t,r}蘊涵由條件可推得即因此xmin{t,r}∈∨qkμ,這表明(I2)成立,故μ為X的(∈,∈∨qk)-模糊蘊涵理想。□ 推論1設μ為BCK-代數X的一個(∈,∈∨qk)-模糊蘊涵理想,如果,則μ必為X的一個模糊蘊涵理想。 證明設μ為X的(∈,∈∨qk)-模糊蘊涵理想且如果存在a∈X使得μ(0)<μ(a),則由可得μ(0) 因此μ是X的一個模糊蘊涵理想。□ 下面討論 (∈,∈∨qk)-模糊理想與 (∈,∈∨qk)-模糊蘊涵理想的關系。 定理3BCK-代數X的任何(∈,∈∨qk)-模糊蘊涵理想必是X的(∈,∈∨qk)-模糊理想。 證明令μ為X的(∈,∈∨qk)-模糊蘊涵理想,則在(I2)式中用x替代y便有 (x?z)t=((x?0)?z)t=((x?(x?x))?z)t∈μ且zr∈μ蘊涵xmin{t,r}∈∨qkμ,這表明μ滿足(I-2)。結合(I1),μ為X的一個(∈,∈∨qk)-模糊理想。□ 下例說明定理3的逆不真。 例2設X是例1中的BCK-代數。定義模糊子集μ:X→[0,1]如下:μ(0)=μ(2)=0.5 且μ(1)=μ(3)=μ(4)=0.3。可以驗證模糊子集μ為(∈,∈∨q0.1)-模糊理想,但它不是 (∈,∈∨q0.1)-模糊蘊涵理想,因為 ((1?(3?1))?2)0.4=00.4∈μ,20.5∈μ,1min{0.4,0.5}?μ且μ(1)+min{0.4,0.5}+0.1=0.8<1,于是即 下列定理說明對于蘊涵BCK-代數而言,定理3之逆是成立的。 定理4如果X是蘊涵BCK-代數,則X的每一個(∈,∈∨qk)-模糊理想都是X的 (∈,∈∨qk)-模糊蘊涵理想。 證明因為X是一個蘊涵BCK代數,所以由文獻[2]知,對任意x,y∈X,有x=x?(y?x)。設μ為X的一個 (∈,∈∨qk)-模糊理想,則依(I-2)可知,對任意x,y∈X和t,r∈(0,1],zr∈μ與 (x?z)t∈μ可蘊涵xmin{t,r}∈∨qkμ。因為x?z=x?z=(x?(y?x))?z,所以 ((x?(y?x))?z)t=(x?z)t∈μ與zr∈μ蘊涵xmin{t,r}∈∨qkμ,故(I2)成立。結合(I-1)有,μ是X的一個(∈,∈∨qk)-模糊蘊涵理想。□ 定理5BCK-代數X的模糊子集μ是X的(∈,∈∨qk)-模糊蘊涵理想當且僅當: 證明假設μ是X的一個(∈,∈∨qk)-模糊蘊涵理想且是得U(μ;t)≠? 。令x∈U(μ;t),則μ(x)≥t,因此由(I3)可知,從而得0∈U(μ;t)。令(x?(y?x))?z∈U(μ;t),z∈U(μ;t),則μ((x?(y?x))?z)≥t且μ(z)≥t。按照(I4)得t,進而x∈U(μ;t),因此U(μ;t)是X蘊涵理想。 反之,假設μ是滿足(I5)的X之模糊子集。如果(I3)不成立,則存在a∈X使得于是對某些成立,由此可得a∈U(μ;t),所以U(μ;t)≠? 且U(μ;t)是X的蘊涵理想。但由μ(0) 若在定理5中取k=0,則有如下推論: 推論2BCK-代數X的模糊子集μ為X的(∈,∈∨q)-模糊蘊涵理想X當且僅當對任意t∈(0,0.5],當U(μ;t)≠?時,U(μ;t)是X的蘊涵理想。 定理6如果I是BCK-代數X的一個蘊涵理想,定義X的模糊子集μ如下: 證明注意到 為X的一個蘊涵理想。由定理6知,μ是X的一個(∈,∈∨qk)-模糊蘊涵理想。□ 推論3如果I是BCK-代數X的一個蘊涵理想,定義X的模糊子集μ如下: 其中,t1∈[0.5,1]且t2∈(0,0.5),則μ為X的一個(∈,∈∨q)-模糊蘊涵理想。 定理7對任意k1,k2∈(0,1]且滿足k1 證明結論是顯然的。□ 下例說明定理7的逆不成立。 例3考慮例2中X的模糊子集μ,容易驗證μ是X的一個(∈,∈∨q0.8)-模糊蘊涵理想。但由例2可知,它不是X的(∈,∈∨q0.1)-模糊蘊涵理想。 對于X的任一模糊子集μ及t∈(0,1],定義X的兩個子集如下: 定理8設μ為BCK-代數X的(∈,∈∨qk)-模糊蘊涵理想,則對任意當Qk(μ;t)≠? 時,Qk(μ;t)為X的一個蘊涵理想。 證明假設μ是X的一個(∈,∈∨qk)-模糊蘊涵理想,令使得若x∈Qk(μ;t),則即μ(x)+t+k>1。由(I3)并注意到有: 即μ(0)+t+k>1,于是 0tqkμ,因此 0∈Qk(μ;t)。令 (x?(y?x))?z∈Qk(μ;r)并且z∈Qk(μ;r),則 ((x?(y?x))?z)tqkμ,ztqkμ,即μ(z)+t+k>1且μ((x?(y?x))?z)+t+k>1。利用(I4)并注意到,并記,那么: 即μ(x)+t+k>1,于是xtqkμ,因此x∈Qk(μ;t)。綜上所述,對任意當Qk(μ;t)≠? 時,Qk(μ;r)是X的蘊涵理想。□ 定理9BCK代數X的模糊子集μ為X的(∈,∈∨qk)-模糊蘊涵理想當且僅當對任意t∈(0,1],當是X的蘊涵理想。 證明假設μ是X的一個(∈,∈∨qk)-模糊蘊涵理想,且令t∈ (0,1]使得如果則根據定理5可知,為X的蘊涵理想。如果則依據定理6可知,是X的一個蘊涵理想。總之,對任意為X的蘊涵理想。 反之,假設μ是X的一個滿足題設的模糊子集。如果存在a∈X使得對某些成立,則但 0?U(μ;t)。因此故,即矛盾,所以對任意x∈X成立。若存在a,b,c∈X使得那么對某些成立。因為且 (a?(b?a))?c∈U(μ;r)?所以這表明是X的蘊涵理想。但從μ(a) 根據定理2可知,μ是X的一個(∈,∈∨qk)-模糊蘊涵理想。□ 在定理9中令k=0,可得如下推論。 推論4對于BCK-代數X的模糊子集μ,下列條件是等價的: (1)μ是X的一個(∈,∈∨q)-模糊蘊涵理想。 (2)對任意t∈(0,1],當是X的蘊涵理想。 下面給出(∈,∈∨qk)-模糊蘊涵理想的一個刻畫。 定理10如果μ是BCK-代數X的一個(∈,∈∨qk)-模糊理想,則μ是X的(∈,∈∨qk)-模糊蘊涵理想當且僅當對任意x,y∈X,有: 證明假設μ是X的一個(∈,∈∨qk)-模糊蘊涵理想,則依定理2有: 對任意x,y∈X成立,從而(I6)成立。 反之,設μ是滿足(I6)的 (∈,∈∨qk)-模糊理想,則依文獻[16]中的定理 2(F-4)可知,μ(x?(y?x))≥結合(I6)可知,對任意x,y,z∈X,有: 從而(I4)成立。因為μ是X的(∈,∈∨qk)-模糊理想,所以依文獻[17]中的定理2(F-3)可知,(I3)成立。總之,μ為X的一個(∈,∈∨qk)-模糊蘊涵理想。□ 模糊邏輯是多值邏輯理論的一個延伸。模糊邏輯中的一些算子,如∨、∧、?、→,是通過真值表來定義的,并且擴展原理可以應用于派生出算子的定義。在模糊邏輯中,模糊命題ψ的真值表示為[ψ]。對于給定的論域X,本文要用到的模糊邏輯和相應的集理論符號如下: (2)中的真值規則是基于Lukasiewicz蘊涵算子的連續值邏輯系統。當然,還存在許多其他蘊涵算子,最常用的蘊涵算子列舉如下: Ying在文獻[19]中引入了不分明化拓撲的概念,并研究了其相關性質。本文將他的思想應用于BCK-代數的結構討論中,定義不分明化蘊涵理想。 定義8BCK-代數X的模糊子集μ叫作X的不分明化蘊涵理想,如果它滿足: (1)對任意x∈X,有╞(x∈μ)→(0∈μ)。 (2)對任意x,y,z∈X,有╞ (((x?(y?x))?z∈μ)∧(z∈μ)→(x∈μ))。 顯然,定義8中的條件(1)和(2)分別等價于(F1)和(F3)。在文獻[20]中引入了t-重言式的概念,即╞t ψ當且僅當[ψ]≥t對所有賦值都成立。 定義9設X是BCK-代數且t∈(0,1],X的模糊集μ叫作X的t-蘊涵的模糊蘊涵理想,如果它滿足: (1)對任意x∈X,有╞t(x∈μ)→(0∈μ)。 (2)對任意x,y,z∈X,有╞t(((x?(y?x))?z∈μ)∧(z∈μ)→(x∈μ))。 設R是一個蘊涵算子,顯然μ是X的t-蘊涵的模糊蘊涵理想當且僅當它滿足對任意x,y,z∈X,有: 定理11對BCK-代數X的任一模糊子集μ,下列結論成立: (1)若R=RGR,則μ是X的一個0.5-蘊涵的模糊蘊涵理想當且僅當μ是X的模糊蘊涵理想。 ①對任意x∈X,有成立; ②對任意x,y,z∈X,有(y?x)?z),μ(z),1}。 證明(1)是明顯的。 (2)假設μ是X的一個-蘊涵的模糊蘊涵理想,則對任意x,y,z∈X,有且對于第一個不等式,有μ(0)≥μ(x)或,因此對任意x∈X有成立。第二個不等式蘊涵著 min{μ((x?(y?x))?z),μ(z)}≤μ(x)或者從而對任意x,y,z∈X成立。由定理2可知,μ是X的(∈,∈∨qk)-模糊蘊涵理想。 反之,假設μ是X的(∈,∈∨qk)-模糊蘊涵理想。由(I3),若則R(μ(x),μ(0))=1≥G否則由(I4),如果 則μ(x)≥ min{μ((x?(y?x))?z),μ(z)},進而對任意x,y,z∈X成立。若 (3)假設μ是X的一個-蘊涵的模糊蘊涵理想,則(i)對任意x∈X成立,并且(ii)對任意x,y,z∈X,有RcG(min{μ((x?(y?x))?z),μ(z)},成立。條件(i)蘊涵著μ(0)≥μ(x)或1-故從而由 條件(ii)可 知 min{μ((x?(y?x))?z),μ(z)} ≤μ(x) 或 者。因此對任意x,y,z∈X,有: 反之,假設模糊集μ滿足條件①和②。對于條件①,若μ(x)=1,則故R(μ(x),cG如果μ(x)<1,則③成立。 推論5對于BCK-代數X的模糊子集μ,下列結論成立: (1)若R=RG,則μ是X的一個0.5-蘊涵的模糊蘊涵理想當且僅當μ是X的一個(∈,∈∨q)模糊蘊涵理想。 (2)若R=RcG,則μ是X的一個模糊蘊涵理想當且僅當μ滿足下列條件: ①max{μ(0),0.5}≥min{μ(x),1}對任意x∈X都成立; ②對任意x,y,z∈X,有 max{μ(x),0.5}≥min{μ((x?(y?x)?z),μ(z),1}。 隨著數學和計算機科學的發展,作為非經典模糊邏輯代數類的BCK-代數類被人們深入而廣泛地研究。本文建立了模糊點與模糊集之間的屬于與重于更一般關系,從而推廣了BCK-代數的(∈,∈∨q)-模糊蘊涵理想,引入了(∈,∈∨qk)-模糊蘊涵理想的概念,研究了它的相關性質,證明了任何模糊蘊涵理想和任何 (∈,∈∨q)-模糊蘊涵理想都是 (∈,∈∨qk)-模糊蘊涵理想,例證表明反之則不必然;指出了每個(∈,∈∨qk)-模糊理想都是 (∈,∈∨qk)-模糊蘊涵理想,通過實例說明了其逆不真,并進一步說明了蘊涵BCK-代數的 (∈,∈∨qk)-模糊理想與 (∈,∈∨qk)-模糊蘊涵理想是等價的;闡明了對一個(∈,∈∨qk)-模糊蘊涵理想而言,當k在區間[0,1]由小變大時,它仍是(∈,∈∨qk)-模糊蘊涵理想,反之則不然;給出了BCK-代數的(∈,∈∨qk)-模糊蘊涵理想的幾個等價刻畫,其中包含了水平子集在內的3個普通集合的關系;引入了基于蘊涵的BCK-代數的模糊蘊涵理想的概念,討論了3個特殊蘊涵算子誘導的模糊蘊涵理想的特征,獲得了有意義的結論,這些豐富結論足以說明這種關于代數結構的研究是非常有價值的。 [1]Bunder W M.BCK and related algebras and their corresponding logics[J].Journal of Non-Classical Logic,1983,1:15-24. [2]Imai K,Iséki K.On axiom system of propositional calculus[J].Proceedings of the JapanAcademy,1966,42:19-22. [3]Iséki K,Tanaka S.An introduction to the theory of BCK-algebras[J].Mathematica Japonicae,1978,23:1-26. [4]Iséki K,Tanaka S.Ideas theory of BCK-algebras[J].Mathematica Japonicae,1976,21:351-366. [5]Peng Jiayin.Normed BCI-algebras[J].Chinese Quarterly Journal of Mathematics,2011,26(4):543-548. [6]Meng Jie.On ideals in BCK-algebras[J].Mathematica Japonicae,1994(1):143-154. [7]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3):338-353. [8]Xi O G.Fuzzy BCK-algebras[J].Mathematica Japonicae,1991,36:935-942. [9]Meng Jie,Guo Xiu'e.On fuzzy ideals in BCK/BCI-algebras[J].Fuzzy Sets and Systems,2005,149(3):509-525. [10]Jun Y B,Hong S M,Meng Junna,et al.Characterizations of fuzzy positive implicative ideals in BCK-algebras[J].Mathematica Japonicae,1994,40:503-507. [11]JunYB,Roh E H.Fuzzy commutative ideals of BCK-algebras[J].Fuzzy Sets and Systems,1994,64:401-405. [12]Peng Jiayin.Fuzzifying implicative ideals of BCK-algebras based on continuous-valued logic[J].Fuzzy Systems and Mathematics,2015,29(5):1-10. [13]Meng Jie,Jun Y B,Kim H S.Fuzzy implicative ideals of BCK-algebras[J].Fuzzy Sets and Systems,1997,89(2):243-248. [14]Pu Paoming,Liu Yingming.Fuzzy topology I,neighborhood structure of a fuzzy point and Moore-Smith convergence[J].Journal of Mathematical Analysis&Applications,1980,76(2):571-599. [15]Zhang Guangji,Zhang Cheng,Liu Zixin,et al.New kinds of fuzzy ideals in BCI-algebras[J].Fuzzy Optimization&Decision Making,2006,5(2):177-186. [16]Liu Yinping,Xin Xiaolong.(∈,∈ )((∈,∈ ∨q),(-∈,-∈ ∨ -q))-fuzzy implicative ideals of BCK-algebras[J].Fuzzy Systems and Mathematics,2010,24(6):48-54. [17]Liu Chunhui.Generalized(∈,∈∨q)-fuzzy ideals in BCK-algebras[J].Chinese Quarterly Journal of Mathematics,2015,30(3):373-380. [18]Liu Chunhui.(∈,∈∨q)-fuzzy soft ideals in BCK/BCI-algebras[J].Journal of Zhejiang University:Science Edition,2015,42(3):256-260. [19]Ying Mingsheng.A new approach for fuzzy topology I[J].Fuzzy Set and Systems,1991,39(3):303-321. [20]Ying Mingsheng.On standard models of fuzzy modal logics[J].Fuzzy Sets and Systems,1988,26(3):357-363. 附中文參考文獻: [12]彭家寅.基于連續值邏輯之BCK-代數的不分明蘊涵理想[J].模糊系統與數學,2015,29(5):1-10. [16] 劉 銀 萍, 辛 小 龍.BCK-代 數 的 (∈,∈)((∈,∈∨q),-模糊蘊涵理想[J].模糊系統與數學,2010,24(6):48-54.
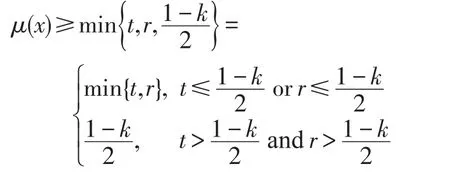
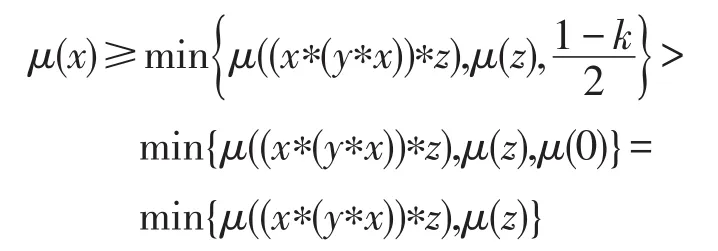
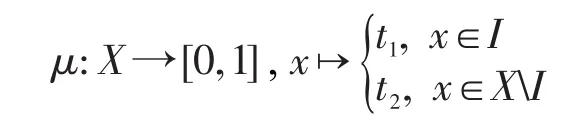
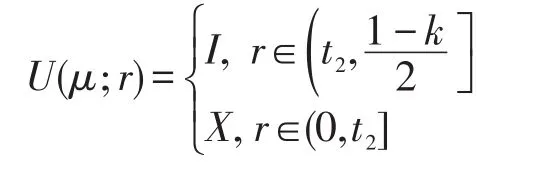
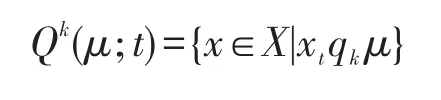
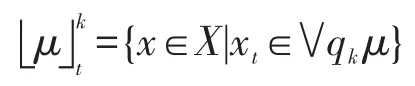
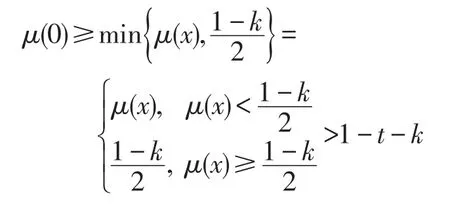
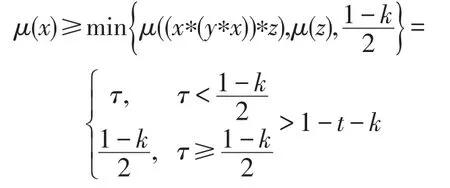
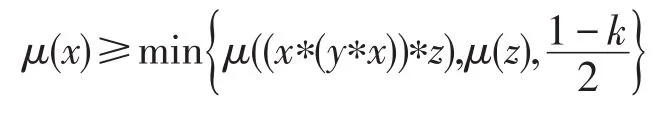

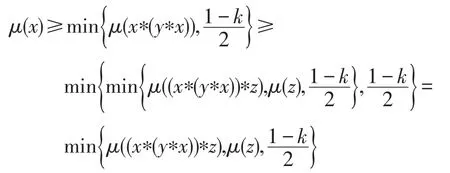
4 基于蘊涵的BCK-代數的模糊蘊涵理想


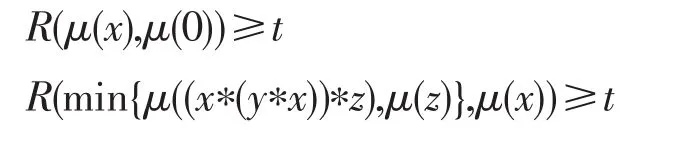


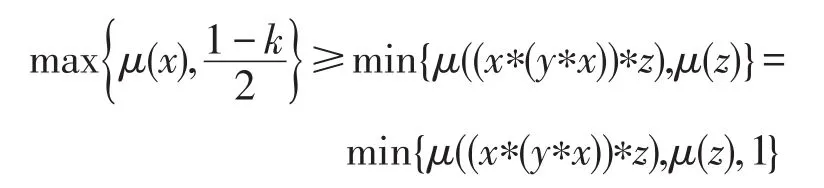

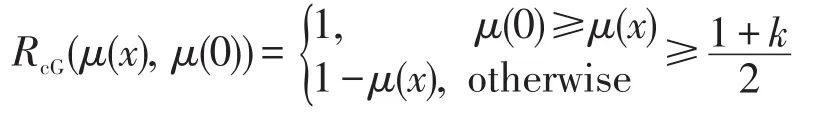

5 結論

