圖松弛優化聚類的快速近似提升方法*

謝　磊，王士同

江南大學 數字媒體學院，江蘇 無錫 214122

1　引言

聚類是數據挖掘、統計機器學習和科學發現的首要問題。在過去幾十年中，已經開發了各種各樣的方法來解決聚類問題[1-4]。例如在完成一些圖像分割任務時，其中的數據聚類問題便是通過高階相關聚類[5]來解決。作為解決NP-hard組合優化問題的替代方案，半定規劃松弛被提出。基于半定規劃松弛的方法相比于光譜/特征向量方法具有一定優勢[6-7]，因為該方法的附加約束迫使優化過程找到效果更好的解決方案。然而，這一約束也帶來了很大的負面效果：迭代終止標準對聚類結果有顯著影響。與之相比，基于圖松弛優化聚類（graph-based relaxed clustering，GRC）[8]算法表現出很好效果。通過歸一化剪切改進[6]中引入的歸一化目標，簡化了計算，使得聚類任務可以作為二次規劃解決。聚類效果在處理復雜的集群時有所改善，且實現也非常簡單。

雖然GRC算法有許多優點，但其并不能和經典算法相媲美，例如層次聚類以及k-means算法，它們都在大規模數據挖掘中得到很好的應用。原因很簡單，此算法由于計算矩陣的逆會消耗多項式計算時間，在計算高維大數據時會顯得非常吃力甚至不可行。

本文主要專注于設計對GRC算法的快速近似改進算法，即主要對GRC算法做速度提升。正如在涉及計算瓶頸的數據挖掘中的許多情況一樣，本文的目標是找到一種有效的預處理器，減少輸入到該瓶頸的數據結構的大小（參見文獻[9-10]）。此預處理步驟可以考慮許多方式，例如，可以對數據進行多種形式的二次采樣，隨機選擇數據點或根據某種形式進行分層選取。另一個選擇是用少量點（即“代表點”）替換原始數據集，目的是捕獲數據相關結構。本文主要提供了兩個這樣的預處理方式。第一個是將k-means應用于對初始數據的縮減步驟，第二個是使用文獻[11]中的隨機投影樹（random projection tree，RPTree）。實驗顯示，通過這兩種預處理，彌補了GRC算法的不足，尤其在速度方面有顯著改進。同樣，在處理一些較大規模數據時性能得到了提高。

2　相關準備

2.1　GRC算法

給定n個數據點X1,X2,…,Xn，每個Xi∈Rd。令鄰接圖G=(V,E)定義為無向圖，其中第i個頂點對應于數據點Xi。對于每個邊緣(i,j)∈E，本文用權重aij來表示數據點Xi和Xj的親和度（或相似度）。并將矩陣作為鄰接矩陣。

GRC算法的目的同樣是將數據分為多個類，使得每一數據樣本屬于且僅屬于某一類。各種聚類算法用不同的方式將這種分割問題形式化。作為解決NP-hard組合優化問題的一個替代方案，文獻[12]提出了半定規劃松弛方法。同樣的，Lee等人在文獻[8]中提出了基于圖松弛優化算法，需要注意的是，其中歸一化剪切（normalized cut，NC）[13]被寬限到廣義特征值系統：

其中e′=(1,1,…,1),L=D-A作為拉普拉斯矩陣。e的維度為數據點的數目，D、A分別為圖的度矩陣和鄰接矩陣。

式（1）中的兩個約束將最優解限制在二進制分區上。為了克服這個短缺，Lee等人進一步松弛式（1）得：

其中Q=e′，ζ為常數，這就是所謂的GRC算法。式（2）是它的二次規劃（quadratic programming，QP）形式。作者通過使用拉格朗日乘數法又進一步將其簡化為如下形式：

本文聚類問題的優化以封閉形式求解，無需任何迭代即可找到L的特征屬性。但如果L是半正定，會出現一些問題，所以通過在L中的對角線項添加正值α來近似替代L，以此來保證L是正定的。當然，在式（3）之前還可以根據對數據的了解做更多約束條件，增強對聚類的區分。通過y，可以很容易地知道有多少個聚類存在，直觀地區分它們。為了最后方便對比，可以對y進行k-means運算得到比較統一的聚類標簽。可見，GRC算法是自適應的（即它不需要預先設定聚類的數量）和直接的（即所有聚類的區分可以僅通過一次單一的計算完成）。但是此方法在計算矩陣的逆時，消耗多項式時間，不難想象，隨著數據量的增多，矩陣維度的增大，時間消耗將逐漸變得不可接受。因此，在下節將給出快速近似提升方面的內容。

關于GRC算法具體過程詳解如下所示。需要注意的是，在σ的選值方面，不同數據集則選值不同，一般可對各維度計算標準差后求均值得出。本文方法則是在循環計算每一維度時，根據所得數據實時運算求出標準差。

算法1基于圖松弛優化（GRC）算法

輸入：n個數據點

輸出：輸入數據的簇標記。

1.計算出鄰接矩陣A：

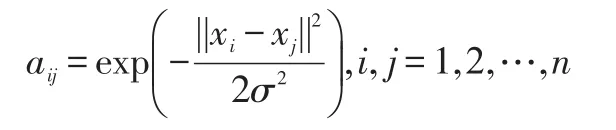
2.2　快速近似方法介紹

文獻[17]巧妙地選擇以與其規范成比例的值對Gram矩陣的列進行采樣的方案，從而代替均勻采樣這一步驟。因為這對Gram矩陣在近似誤差的約束上做出讓步，所以該方法可能需要選擇較多的列以實現較小的近似誤差。其誤差界限可由如下公式表示：

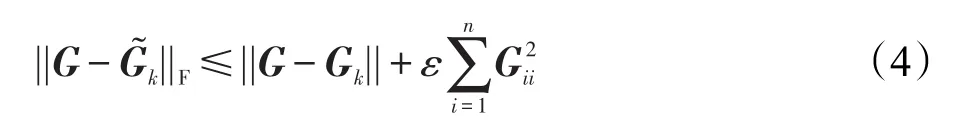
其中，Gk是G秩為k的最佳近似，這形成了用于近似Gram矩陣的約束。由于來自G的數量為n的采樣列，數量級為且該算法具有級的計算復雜度。從式（4）的右側可看出，為了獲得較小的近似誤差則需要非常小的ε，這也使得將要選擇的行數變大。例如，當使用高斯內核時會按照O(n)的量級增長，因此預期采樣列數為O(n)。本文的快速近似方法則做了相對改進，避免像Nystro?m方法的較高內存需求，且在處理平衡性較低的數據集時，因較小聚類被遺漏所導致的數值穩定性問題也得到較好解決。

3　GRC算法的快速近似改進

本章將介紹對GRC算法的快速近似提升的算法框架。對于這一算法的改進，重點放在其建立鄰接矩陣和矩陣求逆的時間優化上。對于此問題的解決，最為直接有效的方式便是通過縮小數據量來實現。文中算法主要是由預處理步驟和GRC算法步驟組成。根據GRC算法輸出的錯誤聚類率與輸入失真之間的量化關系，便可在執行GRC算法之前，選取合適的預處理方式，使得調用原始數據的失真最小化。本文給出兩種處理方法：第一種是基于k-means的數據預處理方式，第二種則基于RPTree。此外，這兩種方式主要具有有利的計算性質和實現簡單等優點。算法過程可簡單概括為圖1所示。

3.1　k-means對GRC算法的快速提升

矢量量化是為了在最小化失真度量的情況下，選出表示數據集的最佳代表點集合[22]。當失真測量使用均方誤差時，矢量量化中最常用的算法是kmeans，因其具有理論支持以及簡單等多方面的優點。k-means算法采用迭代過程，在每次迭代時，算法將每個數據點分配給最近的質心，并重新計算聚類質心。當均方誤差的總和穩定時，則程序停止，以此可得到很好的聚類中心作為數據代表點。使用kmeans作為聚類的預處理器，選出數據代表點來進行之后的GRC運算。以此，提出了一種“基于k-means的快速近似GRC算法”（KAGRC）算法。算法過程如下所示。

算法2KAGRC：(x1,x2,…,xn,k)

輸入：n個數據點k個代表點。

2017年，我國甘薯總產量7 057.1萬t,按照55%的加工比例和20%的產品原料比,當年我國甘薯加工品產量約為780萬t．戴起偉等[5]估算結果顯示,當前我國國內甘薯加工產品消費量約在500萬t以上,因此，粗略估算,我國甘薯加工品的年出口水平應在200～280萬t之間．

輸出：輸入數據的聚類標簽label。

1.將x1,x2,…,xn數據類別定義為k，進行k-means計算。

（1）計算得出的聚類中心為y1,y2,…,yk，將其作為k個代表點。

（2）構建一個對應表，將每個xi與最近的聚類質心yi相關聯。

2.對聚類質心y1,y2,…,yk進行GRC算法運算，從而得到每一yi對應的聚類簇標記y，于是可直觀得到聚類情況，了解聚類數目以及大體數量。

3.通過建立的對應表以及yi對應的聚類簇標記得到每一xi所對應的聚類簇標記label。

在KAGRC算法中，第一步k-means的計算復雜度是O(knt)，其中t表示迭代次數。第二步的復雜度不小于O(k3)，第三步復雜度為O(n)，則可知KAGRC的復雜度為O(k3)+O(knt)。

3.2　RPTree對GRC算法的快速提升

在這一方法中，則是用RPTree對k-means進行替代，即通過隨機投影這一方式來減少失真[11]。RPTree給出了數據空間的分區，分區的每個單元格中的中心點作為該單元格中大量數據點的代表點。RPTree是基于k維樹（k-dimensional tree，k-d樹）的，這種空間數據結構[23]是通過每次沿著一個坐標遞歸地分割數據空間所得到，并非沿著坐標方向分割，其根據選擇的方向進行隨機投影分割。當前單元格中的所有點都沿隨機方向投影，然后被分割開來。雖然古典kd樹由于對軸平行分裂的限制而縮小了數據空間的維度，但RPTree在處理數據的固有維度方面更加適合，故使用RPTree作為局部失真最小化變換不失為一種不錯的選擇。由此可見，本文的第二種算法將KAGRC算法的步驟1替換為如下的部分內容：

在x1,x2,…,xn上構建一個h級隨機投影樹；將各單元格中數據點的質心y1,y2,…,yk作為k個代表點。

得到本文的第二種改進算法“基于RPTree的快速近似GRC算法”（RAGRC）。

該算法的時間消耗主要是RPTree在進行數據預處理時的建樹部分以及GRC部分，算法的復雜度為O(k3)+O(hn)，其中O(hn)是建立h級隨機投影樹所需的復雜度。

至此，以上內容即為本文算法的主要內容，首先通過k-means或者RPTree對原始數據進行預處理，再通過GRC算法對預處理所得的代表點進行聚類，之后再映射到各點，從而得到數據標簽的快速近似提升方法。

4　實驗分析

實驗中，主要使用兩個量來評估聚類性能：運行時間，以及通過每個數據集的真實簇標記和算法所得簇標記計算出的聚類精度。運行時間即對某一數據集運行一次聚類算法所用時間（在此使用計算機時間）。則在同樣數據集及環境的情況下，耗時越短且聚類精度越高表明算法性能越好。聚類精度的計算方法很多，本文采用較為通俗的做法，這里需要搜索類的排列，則可令表示類情況，和分別表示數據點的真實簇標記和采用聚類算法后所得簇標記。可用公式將聚類精度β定義為：

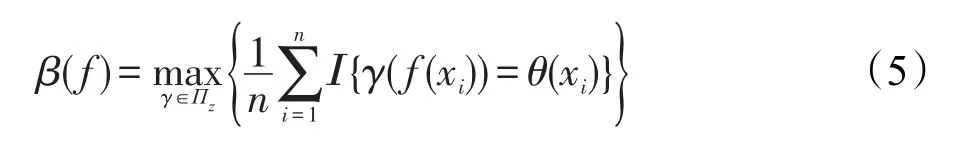
其中，Ι表示指標函數；Πz是z上的所有置換集合。考慮到當聚類數量較多時，式（5）在計算方面受到限制，在這種情況下，從集合Πz中采樣，逐一計算后取出最佳結果使之作為β的最終估計值。在實驗中，如果k<8，窮舉Πz，否則就從中取10 000個樣例。

4.1　實驗平臺及數據集

本文實驗中，所有實驗均使用單一機器作為實驗平臺，同時保證CPU在進行運算時，嚴格控制其他程序對其資源的消耗。實驗平臺的詳細信息如表1所示。本文共9個實驗數據集，分別為5個人造平面數據集DS1、DS2、DS3、DS4、DS5以及4個選自UCI（http://archive.ics.uci.edu/ml/datasets.html）的復雜數據集 mGamma、musk、sensorreadings和 PokerHand。數據集的具體信息如表2所示。需要說明的是，PokerHand數據集由10個類別組成，共有100萬個實例。然而，原始數據集是非常不平衡，其中有6類的總量少于總樣本的1%。本文將較小類別合并在一起，同時保持其中較大類別不變。操作之后，數據集共分為3類，分別對應于樣本總數的50.12%，42.25%和7.63%。

Table 1　Experimental platform表1　實驗平臺

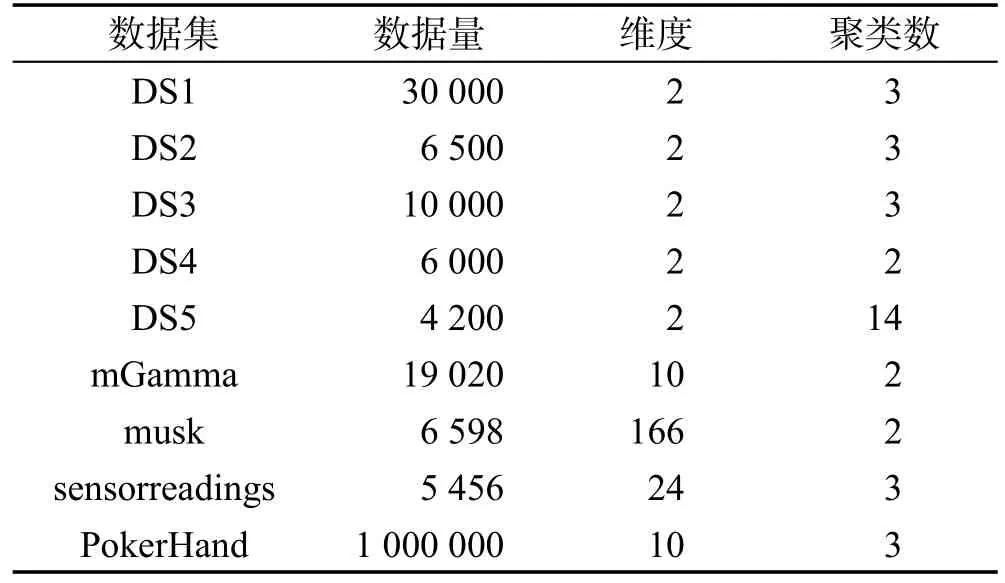
Table 2　Experimental datasets表2　數據集

4.2　速度提升實驗

本節將使用人造數據集DS1、DS2、DS3、DS4，DS5來進行實驗。需要注意的是，本節用到的5個數據集為了在時間上形成對比，都采取了較多數據點。此外，為了證明算法的普遍適用性，這些數據集也具有不同聚類形式，從簡單到復雜，覆蓋面較為廣泛，選取具有代表性。

首先，圖2～圖6給出了原圖及運行GRC算法后和KAGRC算法后的圖解。

從圖中可以看出，相對于GRC算法，KAGRC算法對于各種圖形數據集聚類的效果都非常好。在運行KAGRC算法時，其所對應的縮減率γ為1/8，即各數據集的代表點k為3 750、812、1 250、750和525，其運行時間分別為12 s、0.8 s、1.3 s、0.7 s和0.5 s。相對于直接使用GRC的259 s、8 s、28 s、6.4 s和3 s，速度都有顯著提升。本文實驗具體的情況如表3至表7所示。

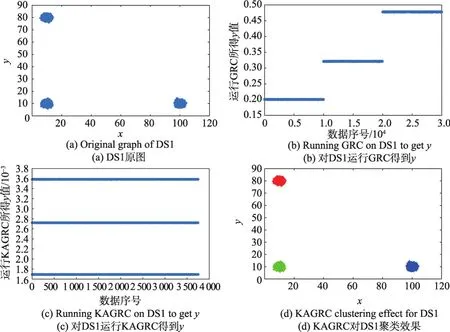
Fig.2　Original graph and experimental graph of DS1圖2　DS1原圖及實驗圖

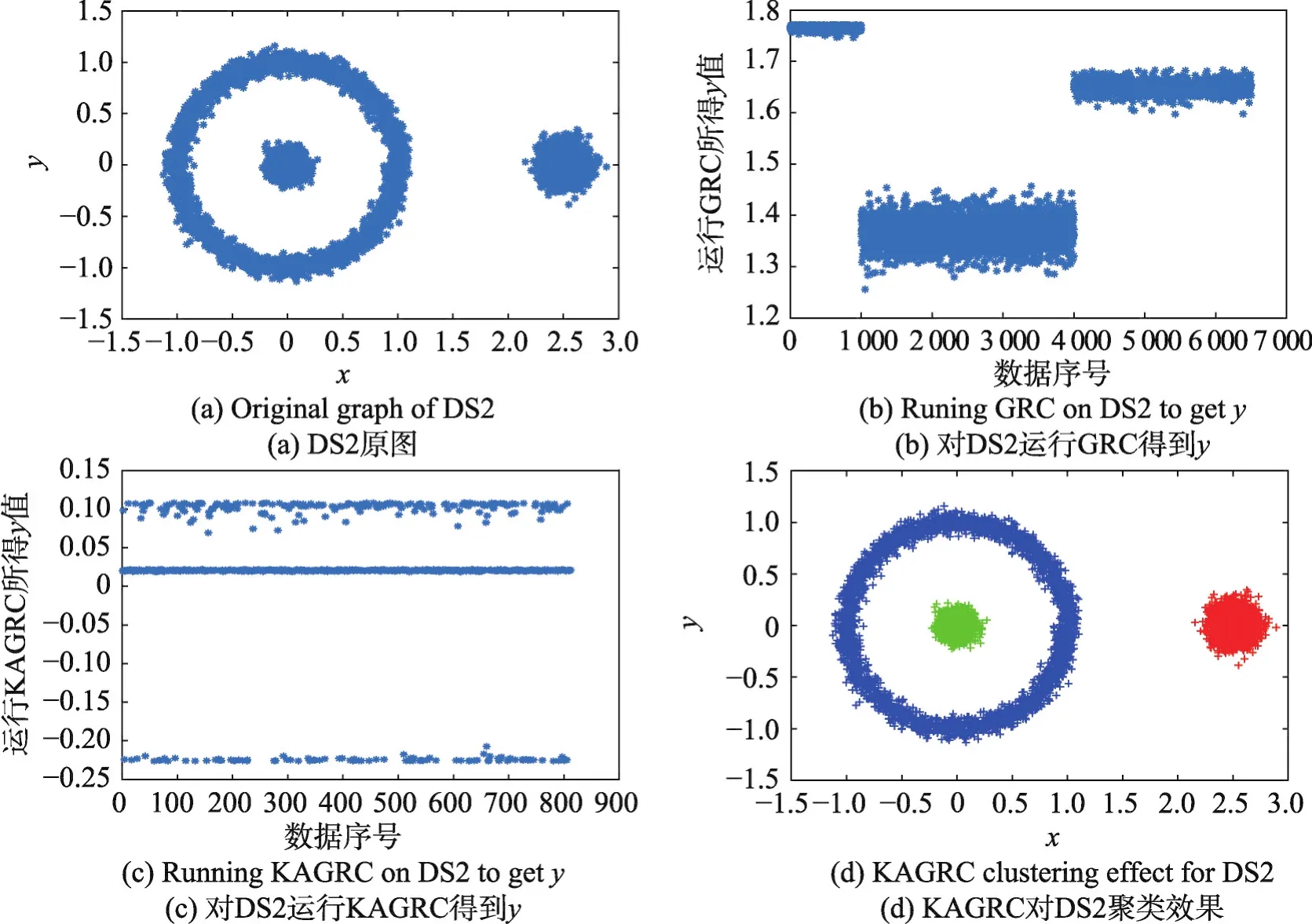
Fig.3　Original graph and experimental graph of DS2圖3　DS2原圖及實驗圖

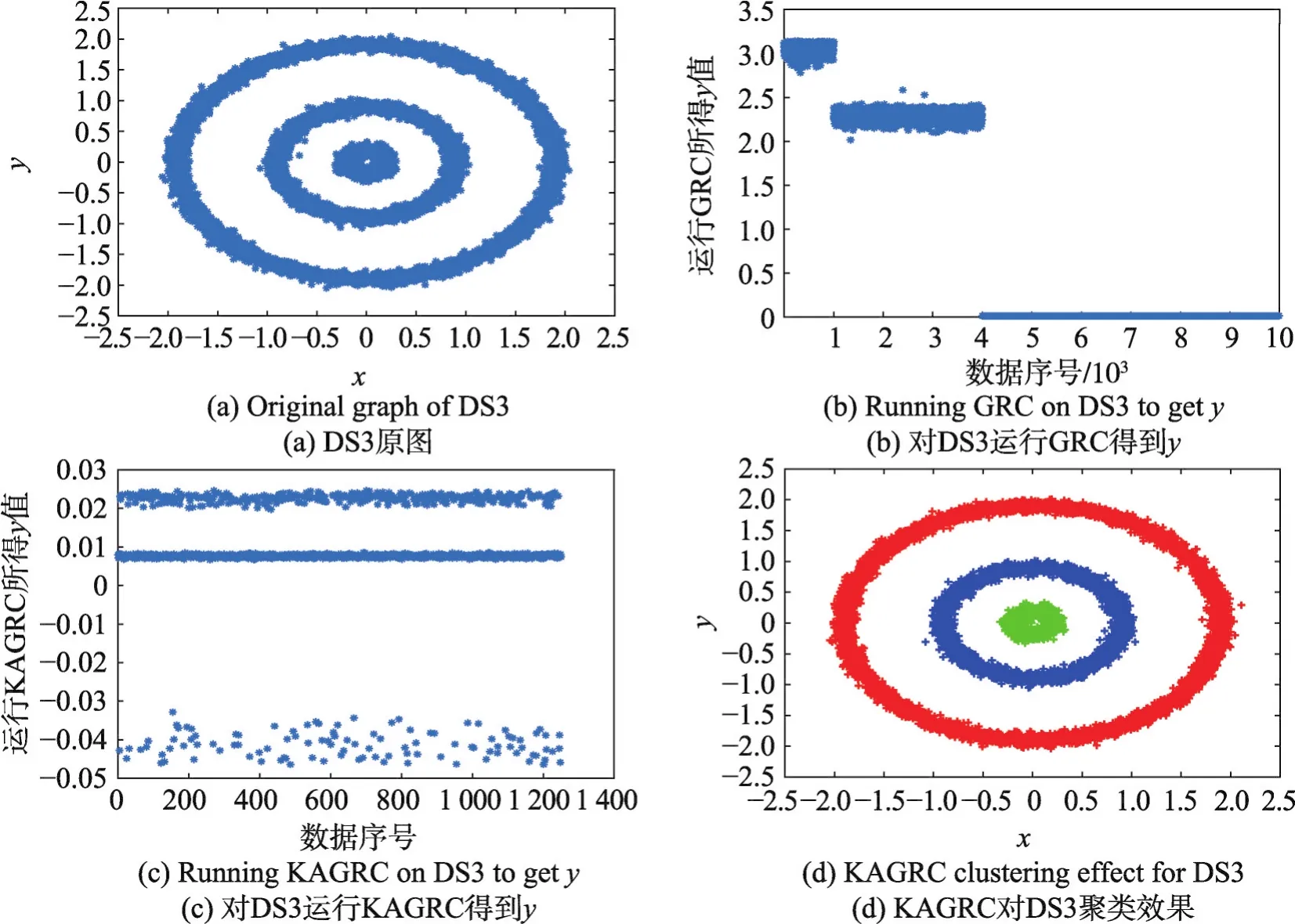
Fig.4　Original graph and experimental graph of DS3圖4　DS3原圖及實驗圖

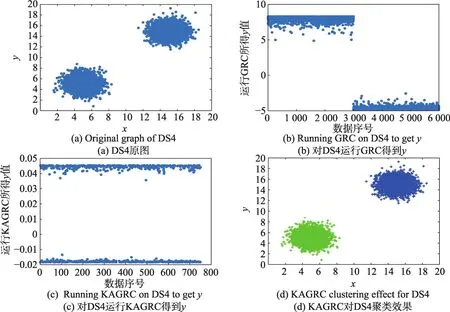
Fig.5　Original graph and experimental graph of DS4圖5　DS4原圖及實驗圖

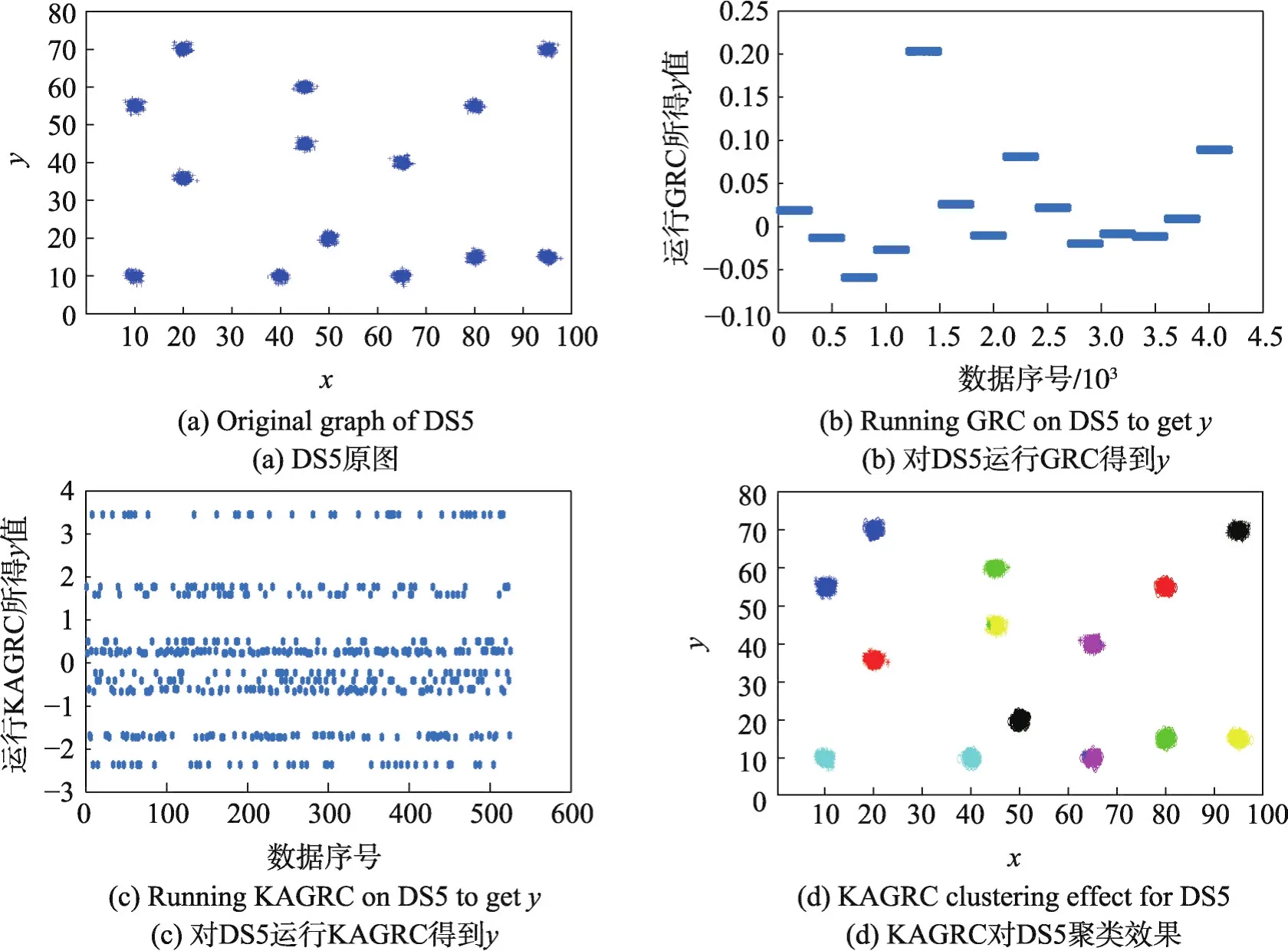
Fig.6　Original graph and experimental graph of DS5圖6　DS5原圖及實驗圖

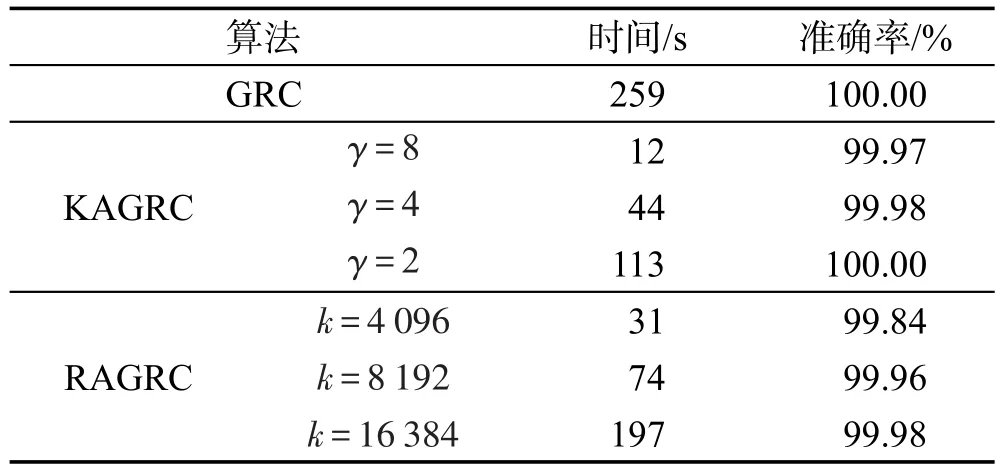
Table 3　Experimental results on dataset DS1表3　數據集DS1的實驗結果

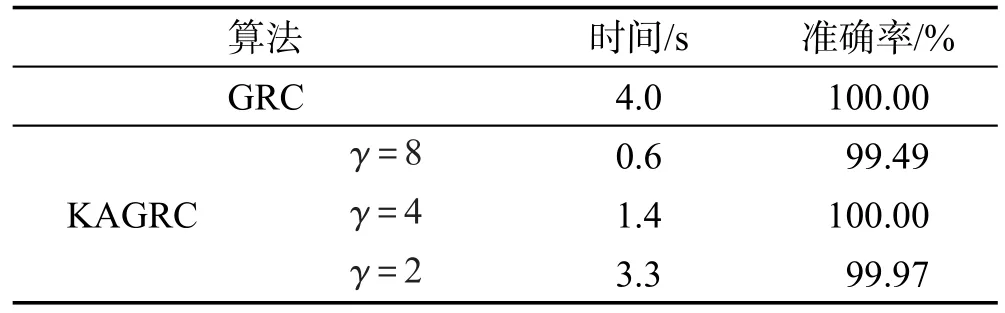
Table 4　Experimental results on dataset DS2表4　數據集DS2的實驗結果

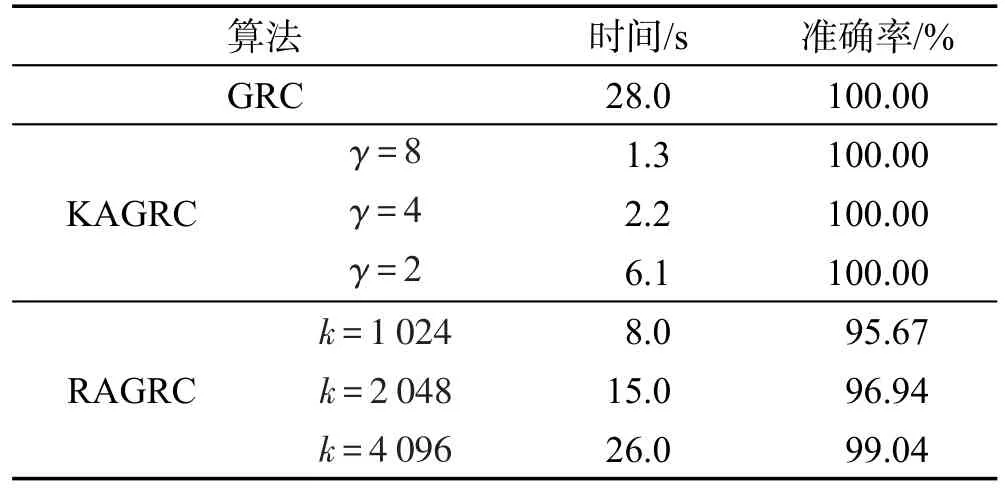
Table 5　Experimental results on dataset DS3表5　數據集DS3的實驗結果

表中，γ為縮減率，k為代表點數。對DS1、DS3等數據樣本量大于10 000的數據集分別進行KAGRC和RAGRC算法實驗。需要注意的是，在隨機投影樹建樹選取代表點時，不能做到和KAGRC算法中所選代表點數目完全相同。因此，RAGRC算法在代表點選取時選擇與KAGRC算法代表點相近數量。在實驗中，由于選點時存在隨機的情況，則會造成每次實驗結果出現小范圍內波動。為此，實驗數據則選取均值作為數據結果，以上每組實驗所記錄數據都是在運行數十次之后計算均值得到。從實驗數據可以明顯看出，同預想一樣，本文提出的KAGRC算法及RAGRC算法同GRC算法相比較，在準確率幾乎不變的情況下，速度明顯提高。當然，隨著縮減率γ逐漸地減小，其代表點隨之增多，算法在時間消耗上也會相應增加。從以上實驗來看，本文算法在保證精度情況下，速度有了非常大的提升，完全達到期望值。

下面的內容主要針對來自UCI的3個真實數據集mGamma、sensorreadings及musk進行實驗。對于sensorreadings數據集，本文選取其中24維度的數據樣本進行實驗，并對其字符進行數字化地處理。實驗中也都對GRC以及k-means算法進行詳細的比較。詳細的實驗結果在表8～表10中分別給出。

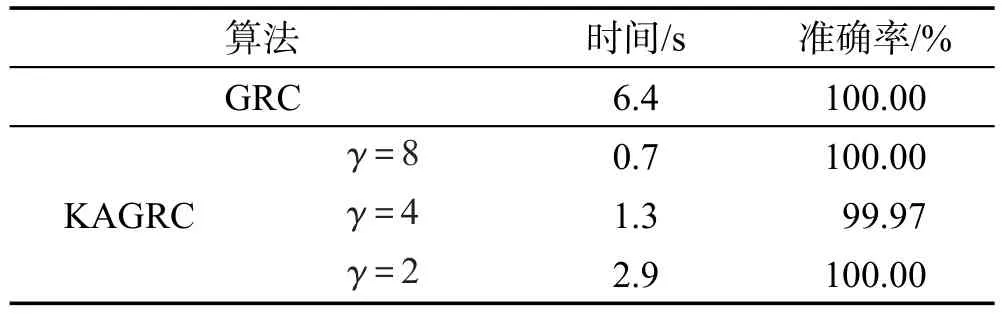
Table 6　Experimental results on dataset DS4表6　數據集DS4的實驗結果

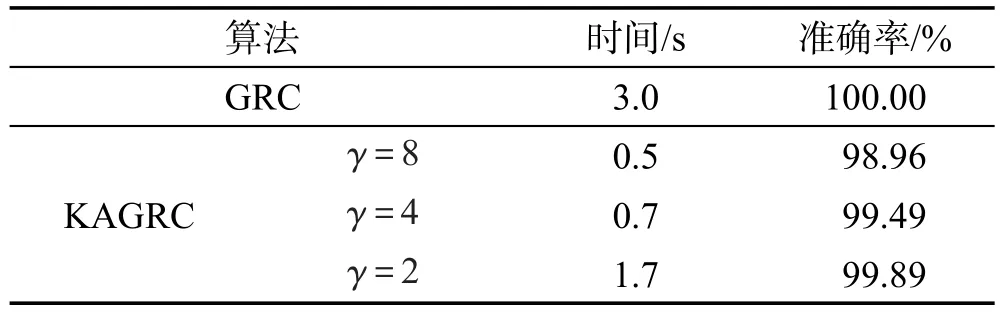
Table 7　Experimental results on dataset DS5表7　數據集DS5的實驗結果

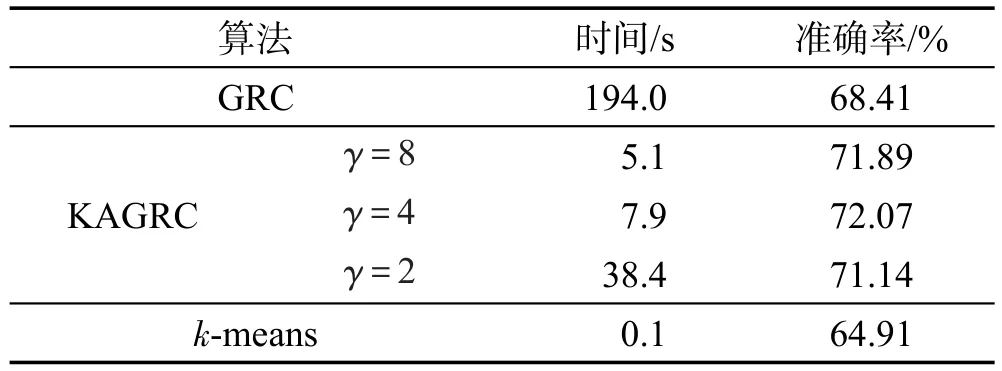
Table 8　Experimental results on dataset mGamma表8　數據集mGamma的實驗結果

從表中數據可看出，本文算法對于真實數據集，相對于GRC算法在速度上顯著改善。對于不同的縮減率，耗時方面會隨著代表點增加而增加，但速度也都遠快于GRC。相對于k-means算法，KAGRC在精度方面同樣表現得非常優秀。

musk數據集的維度為166維，相比于文中的其他數據集，在維度上有所提升。接下來的實驗中，為了進一步展現本文算法的優秀性能，在musk數據集分別對KAGRC、RAGRC以及GRC、k-means等算法的運行結果進行比較。詳細的實驗情況如表10所示。

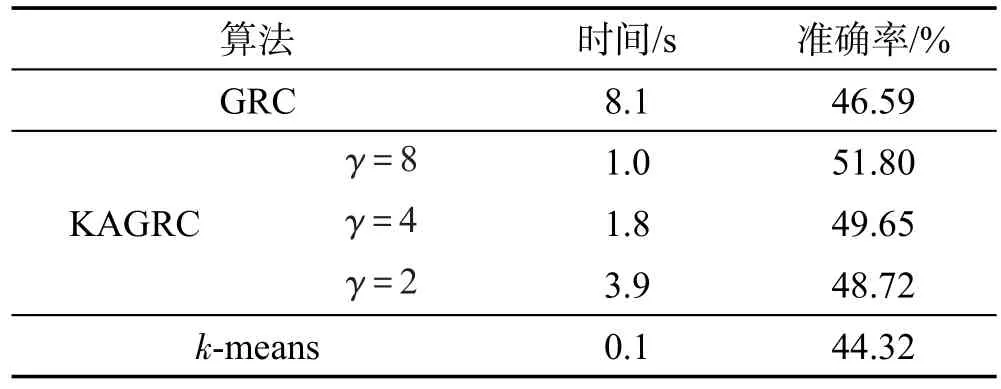
Table 9　Experimental results on dataset sensorreadings表9　數據集sensorreadings的實驗結果

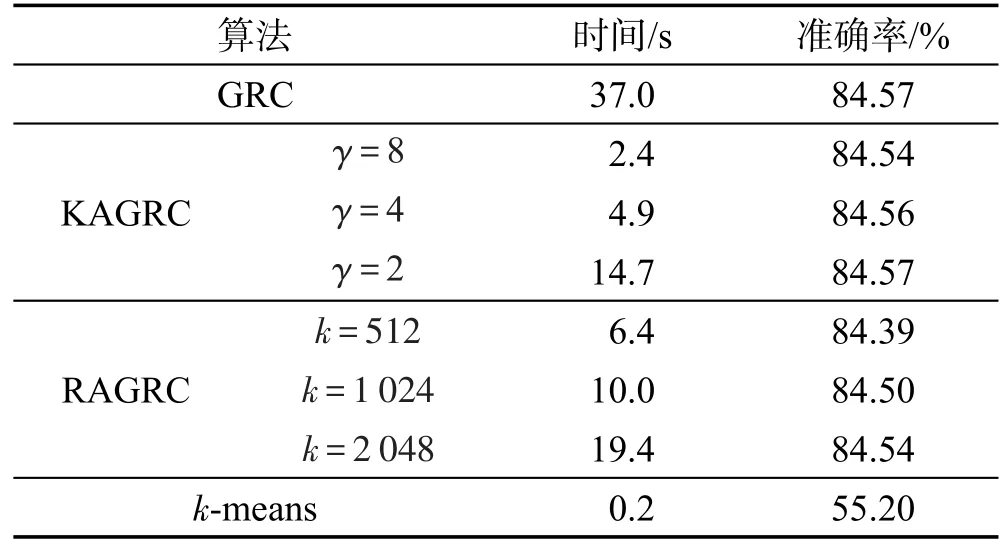
Table 10　Experimental results on dataset musk表10　數據集musk的實驗結果

從表10的實驗結果不難看出，KAGRC和RAGRC算法在精度方面已經遠遠甩開k-means算法。也可注意到，兩種算法在縮減率γ減小，即代表點k的數量增大時，其準確率也同樣是穩步提升。可以明顯看到，在KAGRC算法中，當縮減率γ為2時，其對應的精度已經同GRC精度完全相同。同樣，在RAGRC算法中，當代表點k為2 048時，其精度也和GRC精度非常相近。反觀時間消耗，KAGRC以及RAGRC算法無論縮減率及代表點如何取值，都遠小于GRC算法。同樣，隨著縮減率γ減小，或者代表點k的數量增大時，算法的消耗時間也在合理地隨之增加。同之前實驗相同，本節實驗所得數據結果也是多組實驗后取均值得到。

4.3　百萬級數據可行性實驗

本節將對百萬量級的PokerHand數據集進行實驗分析，以說明本文算法對百萬量級數據操作的可行性。由于數據集樣本量過大，受實驗環境的限制，無法在同等條件下進行GRC運算作為實驗的對比選項，但是可以用其他方式來提供一個粗略的上限。在此，可將聚類問題作為一個分類問題去看待，并且選取最先進的分類算法，即隨機森林（random forest，RF）算法[24]，以此算法所得結果來作為對比的取值。對于RF算法，選取其訓練數據集的大小為25 010，測試數據集大小為1 000 000。同樣，在實驗中也用k-means算法同本文算法進行對比，其中需適量增加k-means的迭代次數，以便運行時間與文中算法的運行時間相同，從而保證遵循實驗對比的單一變量原則。表11是詳細的實驗結果。

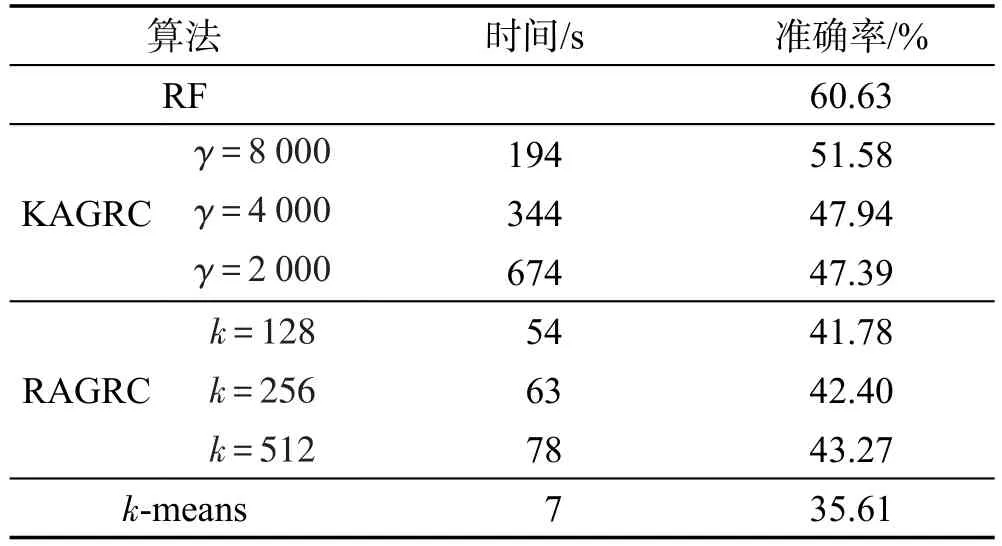
Table 11　Experimental results on dataset PokerHand表11　數據集PokerHand的實驗結果

實驗表明，k-means算法在增加迭代次數后并沒有顯著提高準確率。同時，結果顯示，算法KAGRC和RAGRC中的數據減少并沒有嚴重降低聚類的精度，且在幾分鐘內完成算法計算。另一方面，相對而言，KAGRC算法一定程度上稍優于RAGRC算法。

5　結束語

本文提出了兩種對基于圖松弛優化聚類的快速近似優化方法。文中算法利用k-means和RPTree首先對數據點進行預分組，并產生一組用于GRC算法的代表點。在實驗階段，對多種樣本量、維度以及類別數數據集的實驗表明，本文算法可以在聚類精度上下小范圍浮動的情況下使GRC算法在速度上得到大幅提升。值得注意的是，本文近似算法能夠使單個機器為大型數據集運行GRC算法。

[1]Dong Qi,Wang Shitong.Improved latent sub-space clustering algorithm and its incremental version[J].Journal of Frontiers of Computer Science and Technology,2017,11(5):802-813.

[2]Gold S,RangarajanA,Mjolsness E.Learning with preknowledge:clustering with point and graph matching distance measures[J].Neural Computation,1996,8(4):787-804.

[3]Li Tao,Wang Shitong.Incremental fuzzy(c+p)-means clustering for large data[J].CAAI Transactions on Intelligent Systems,2016,11(2):188-199.

[4]Cheng Yang,Wang Shitong.A multiple alternative clusterings mining algorithm using locality preserving projections[J].CAAI Transactions on Intelligent Systems,2016,11(5):600-607.

[5]Kim S,Nowozin S,Kohli P,et al.Higher-order correlation clustering for image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,36(36):1761-1774.

[6]Sáez A,Serrano C,Acha B.Normalized cut optimization based on color perception findings:a comparative study[J].Machine Vision&Applications,2014,25(7):1813-1823.

[7]Sookhanaphibarn K,Thawonmas R.Exhibition-area segmentation using eigenvectors[J].International Journal of Digital Content Technology&ItsApplications,2013,7(2):533-540.

[8]Lee C H,Ane O R,Park H H,et al.Clustering high dimensional data:a graph-based relaxed optimization approach[J].Information Sciences,2008,178(23):4501-4511.

[9]Madigan D,Raghavan N,Dumouchel W,et al.Likelihoodbased data squashing:a modeling approach to instance construction[J].Data Mining and Knowledge Discovery,2002,6(2):173-190.

[10]Mitra P,Murthy C A,Pal S K.Density-based multiscale data condensation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(6):734-747.

[11]Dasgupta S,Freund Y.Random projection trees and low dimensional manifolds[C]//Proceedings of the 40th Annual ACM Symposium on Theory of Computing,Victoria,May 17-20,2008.New York:ACM,2008:537-546.

[12]Keuchel J.Image partitioning based on semidefinite programming[D].Mannheim:University of Mannheim,2004.

[13]Shi J,Malik J.Normalized cuts and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelli-gence,2000,22(8):888-905.

[14]Deveci M,Kaya K,U?ar B,et al.Hypergraph partitioning for multiple communication cost metrics:model and methods[J].Journal of Parallel&Distributed Computing,2015,77:69-83.

[15]Karypis G,Kumar V.A fast and high quality multilevel scheme for partitioning irregular graphs[J].SIAM Journal on Scientific Computing,2006,20(1):359-392.

[16]Bādoiu M,Har-Peled S,Indyk P.Approximate clustering via core-sets[C]//Proceedings of the 34th Annual ACM Symposium on Theory of Computing,Montréal,May 19-21,2002.New York:ACM,2002:250-257.

[17]Drineas P,Mahoney M W.On the Nystr?m method for approximating a gram matrix for improved kernel-based learning[J].Journal of Machine Learning Research,2005,6:2153-2175.

[18]Williams C K I,Seeger M.Using the Nystr?m method to speed up kernel machines[C]//Proceedings of the Neural Information Processing Systems,Denver.Cambridge:MIT Press,2001:682-688.

[19]Fine S,Scheinberg K.Efficient SVM training using low-rank kernel representations[J].Journal of Machine Learning Research,2002,2(2):243-264.

[20]Hao P,Wang L,Niu Z.Comparison of hybrid classifiers for crop classification using normalized difference vegetation index time series:a case study for major crops in North Xinjiang,China[J].PLOS One,2015,10(9):e0137748.

[21]Fowlkes C C,Belongie S J,Chung F R K,et al.Spectral grouping using the Nystr?m method[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(2):214-225.

[22]Gray R M,Neuhoff D L.Quantization[J].IEEE Transactions on Information Theory,1998,44(6):2325-2383.

[23]Buaba R,HomaifarA,Kihn E.Optimal load factor for approximate nearest neighbor search under exact Euclidean locality sensitive hashing[J].International Journal of Computer Applications,2013,69(21):22-31.

[24]Breiman L.Random forest[J].Machine Learning,2001,45(1):5-32.

附中文參考文獻：

[1]董琪,王士同.隱子空間聚類算法的改進及其增量式算法[J].計算機科學與探索,2017,11(5):802-813.

[3]李滔,王士同.適合大規模數據集的增量式模糊聚類算法[J].智能系統學報,2016,11(2):188-199.

[4]程旸,王士同.基于局部保留投影的多可選聚類發掘算法[J].智能系統學報,2016,11(5):600-607.