基于CEEMDAN和小波閾值的ECG去噪算法研究

徐陽 羅明璋 李濤

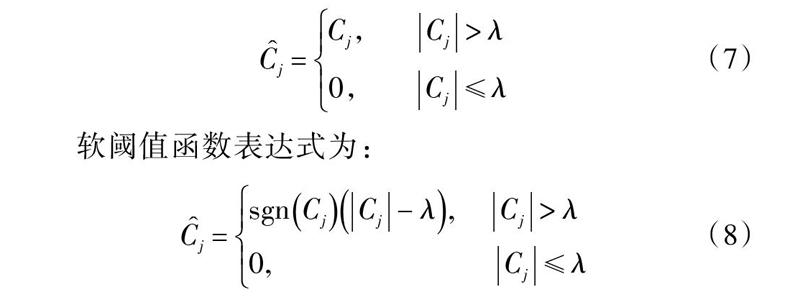
摘 要： 提出一種基于自適應噪聲完備集合經驗模態分解（CEEMDAN）與小波閾值的ECG信號去噪新算法。首先對含噪ECG信號進行CEEMDAN分解，得到從高頻到低頻排序的各個IMF分量，利用自相關法對各IMF分量進行分析，找出以隨機噪聲為主的高頻IMF分量并進行小波閾值去噪；然后統計包括余量在內所有IMF分量的過零率，過零率小于1.5的IMF分量即為基線漂移信號，直接剔除；最后將經過小波閾值去噪的IMF分量與剔除基線漂移之后的其他IMF分量一起進行合并重構，實現ECG信號的去噪和基線校正。用所提算法對MIT?BIH心電數據庫中的ECG信號進行去噪處理，結果表明ECG信號中的隨機噪聲得到很好的抑制，同時獲得了良好的基線漂移校正效果。

關鍵詞： ECG信號； CEEMDAN； 小波閾值； 隨機噪聲； 基線漂移； 去噪算法

中圖分類號： TN911.4?34 文獻標識碼： A 文章編號： 1004?373X（2018）07?0045?04

Study on ECG signal denoising algorithm based on CEEMDAN and wavelet threshold

XU Yang， LUO Mingzhang， LI Tao

（School of Electronics and Information， Yangtze University， Jingzhou 434023， China）

Abstract： A new ECG signal denoising algorithm based on complete ensemble empirical mode decomposition with adaptive noise （CEEMDAN） and wavelet threshold is proposed. The CEEMDAN resolution was performed for the noisy ECG signal to obtain each IMF component sorted from high frequency to low frequency. The autocorrelation method is used to analyze each component of IMF to find out the high?frequency IMF component with random noise， and conduct wavelet threshold denoising. The zero crossing rates （ZCRs） of all IMF components including residue components are calculated. The IMF components whose ZCR is less than 1.5 act as the baseline wander signal， which will be eliminated. The IMF components after wavelet threshold denoising and other IFM components after baseline wander elimination are reconstructed to realize denoising and baceline correction of the ECG signal. The proposed algorithm is adopted to denoise the ECG signal in MIT?BIH ECG database. The results show that the random noise in ECG signal can be effectively suppressed. The good correction effect of baseline wander was obtained.

Keywords： ECG signal； CEEMDAN； wavelet threshold； random noise； baseline wander； denoising algorithm

0 引 言

ECG（心電信號）是一種非線性、非平穩的微弱人體生理電信號，已廣泛應用于臨床心臟疾病診斷。ECG在采集過程中很容易受到各種噪聲的干擾，導致信號出現偏差，使診斷的準確性降低，因此有效抑制心電信號中的噪聲干擾具有重要意義。文獻[1]提出的自適應噪聲完備集合經驗模態分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN）特別適合于ECG類信號的分析處理。本文將CEEMDAN與小波閾值去噪相結合，提出一種新的ECG信號去噪算法。

CEEMDAN的基礎是文獻[2]提出的經驗模態分解（Empirical Mode Decomposition，EMD），EMD可以把復雜信號分解為一系列不同尺度的固有模態函數（Intrinsic Mode Function，IMF），每一個IMF分量包含的頻段范圍隨信號自適應變化。Torres等提出的CEEMDAN算法對EMD作了進一步改進，在EMD分解的每一階段添加自適應白噪聲，通過計算其特定的余量來獲取各個模態分量，其分解過程具有完備性，重構誤差幾乎為零，并且能有效克服模態混疊及減少計算成本。

小波變換[3]是一種較為成熟的信號分析方法，它具有多尺度、低熵性、去相關性等特點，在非平穩信號處理方面具有很大的優勢。由文獻[4]提出的小波閾值去噪方法結合已有的正交小波分解和重構，構建了一套完整的閾值消噪策略，對于隨機噪聲的壓制具有很好的效果。

本文提出一種基于CEEMDAN與小波閾值的ECG去噪算法，基本思想是先對含噪ECG信號用CEEMDAN進行分解，得到從高頻到低頻排序的多個IMF分量，對各個IMF分量進行自相關分析，找出以噪聲為主的IMF分量，并對其進行小波閾值去噪；然后統計包括余量在內所有IMF分量的過零率，對于過零率小于1.5的IMF分量認為是基線漂移信號，直接剔除；最后將經過小波閾值去噪的IMF分量與剔除基線漂移之后的其他IMF分量一起進行重構，實現對ECG信號的去噪和基線校正。用本文方法對MIT?BIH心電數據庫中的ECG數據進行去噪處理，結果表明該方法能夠很好地抑制隨機噪聲，并且使基線漂移得到充分校正。

1 基本原理

1.1 CEEMDAN模態分解

CEEMDAN以EMD分解為基礎。令[Ej（·）]為經EMD分解產生第[j]個IMF分量的算子，[ni（t）]為第[i]次添加的零均值、方差為常數的白噪聲序列，[ε]為信噪比控制系數。CEEMDAN模態分解步驟如下：

1） 向待處理信號[s（t）]中分別加入多次白噪聲序列[ni（t）]，構造出[si（t）=s（t）+εni（t），i=1，2，…，I，]對每個[si（t）]進行EMD分解，直到分解出第1個IMF分量[di1（t）]，定義CEEMDAN的第1個IMF分量為：

2） 在第1階段（即[j=1]），計算第1個余量：

3） 對信號[r1（t）+ε1E1ni（t），i=1，2，…，I，]進行EMD分解，直到分解出第1個IMF分量，定義CEEMDAN的第2個IMF分量為：

4） 在其余每個階段（即[j=2，3，…，J）]，計算第[j]個余量：

5） 對信號[rj（t）+εjEjni（t），i=1，2，…，I，]進行EMD分解，直到分解出第1個IMF分量，定義CEEMDAN的第[j+1]個IMF分量為：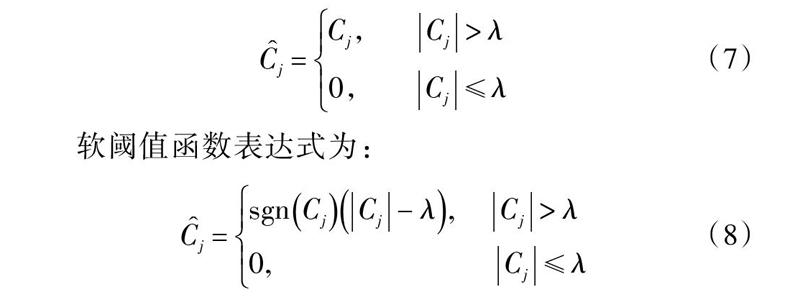

6） 返回步驟4）重復執行，直到所獲得的余量不能再進行EMD分解為止。

CEEMDAN的分解過程是完備的，能對原始信號進行精確重構，并且在每一個EMD分解階段，可通過系數[ε]來選擇合適的信噪比。

1.2 小波閾值去噪

小波變換是一種多尺度信號分析方法，其優良的去噪效果[5]廣受歡迎。小波閾值去噪的基本原理是通過對原始信號[s（t）]選擇合適的小波基和分解層數進行小波變換，得到一組小波分解系數[Cj：]

式中：[W（·）]表示小波變換；[j]為小波分解層數。設置一個臨界閾值[λ，]若小波系數[≤λ，]則認為該系數主要由噪聲產生，去除這部分系數；若小波系數[>λ，]則認為該系數主要由信號產生，保留這部分系數；最后對處理過的小波系數進行重構即可得到去噪后的信號。

小波閾值處理包括硬閾值和軟閾值方法，硬閾值函數表達式為：

軟閾值函數表達式為：

式中：[sgn（·）]為符號函數；[λ]為閾值。

采用小波閾值去噪時，主要通過經驗選取小波基和閾值，不適當的小波基和閾值會直接影響去噪效果。本文在對ECG信號進行小波閾值去噪過程中，通過大量試驗，選取sym8小波基函數進行5層分解，采用啟發式 （heursure）軟閾值取得了較為理想的去噪效果。

2 ECG信號中的隨機噪聲壓制與基線漂移校正

2.1 隨機噪聲壓制

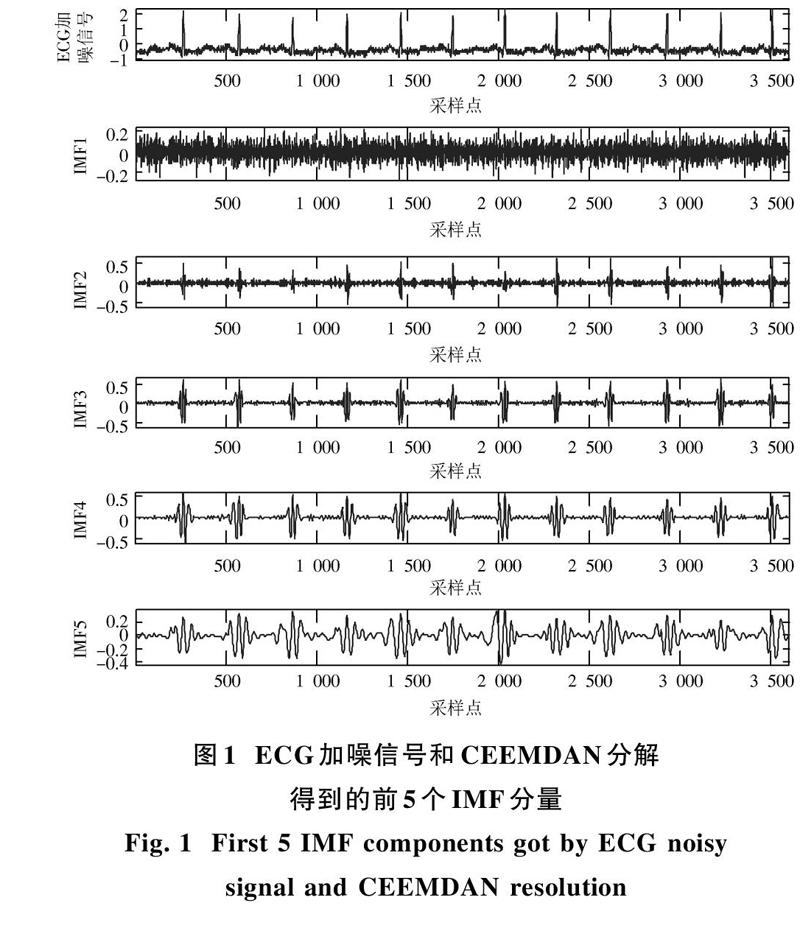
對含噪ECG信號進行CEEMDAN分解，得到從高頻到低頻排序的多個IMF分量，隨機噪聲被分解到前面幾個高頻IMF分量中，只要能確定具體這幾個高頻IMF分量，并對其進行小波閾值去噪，即可有效壓制隨機噪聲。本文利用自相關法對各個IMF分量進行分析，根據自相關函數曲線[6?7]特性判定含有較多隨機噪聲的高頻IMF分量。ECG信號中隨機噪聲的自相關函數曲線是一個尖脈沖，而含噪有效信號的自相關函數曲線的主瓣具有一定的寬度。當IMF分量中含有較多隨機噪聲時，其自相關函數曲線的主瓣會變窄。因此，可以選擇自相關函數曲線中主瓣寬度小于含噪有效信號主瓣寬度的IMF分量，作為含有較多隨機噪聲的高頻分量，并對其進行小波閾值去噪處理。

從MIT?BIH arrhythmia心電數據庫中取得100號ECG原始數據，采樣率為360 Hz，時長為10 s，添加強度為20 dB的高斯白聲，圖1所示為該ECG加噪信號及CEEMDAN分解出的前5個IMF分量。與之相對應的圖2a）、圖2b）分別為隨機噪聲和含噪有效信號的自相關函數曲線，圖2c）～圖2f）分別為前4個IMF分量的自相關函數曲線。從圖2b）中可識別出含噪有效信號的主瓣寬度約為50 ms，由圖2c）～圖2f）可見只有IMF1、IMF2和IMF3的主瓣寬度小于50 ms，說明它們含有較多的隨機噪聲，因此只須選取這3個分量作為小波閾值去噪的對象來壓制隨機噪聲。

2.2 基線漂移校正

基線漂移屬于緩慢變化的超低頻干擾信號，對ECG信號進行CEEMDAN分解時，基線漂移信號被分解到包括余量在內的最后幾個IMF分量中。IMF分量的特性為：在整個數據區間內極值點數目和過零點數目相等或者至多相差1個[8]，通過IMF分量的過零率（單位時間內過零點的數目）可以估算其頻率[9]。由于基線漂移頻率低于1.5 Hz，通過設定閾值為1.5，統計包括余量在內所有IMF分量的過零率，對于過零率小于閾值1.5的IMF分量認為是基線漂移信號，直接剔除，即可實現對基線漂移的校正[10]。

3 ECG信號去噪

3.1 合成ECG信號去噪

圖3a）是從MIT?BIH arrhythmia心電數據庫中取得的100號ECG原始數據（V5導聯，采樣頻率為360 Hz，采樣時間為10 s），添加強度為20 dB的高斯白噪聲，與從MIT?BIH Noise Stress測試數據庫中選取的bw基線漂移信號疊加，得到如圖3b）所示的加噪合成信號。圖3c）所示為直接采用小波閾值去噪結果，圖3d）所示為采用本文提出的CEEMDAN+小波閾值去噪結果，其中小波閾值部分均采用sym8小波基、啟發式軟閾值，小波分解層數為5層。

分解出的前4個IMF自相關函數曲線

為定量說明本文算法的優越性，采用信噪比SNR和均方差MSE作為去噪的性能指標[11]。表1為在不同噪聲強度下計算得到的性能指標數據對比，從信噪比和均方差來看，采用本文算法的去噪效果明顯優于直接采用小波閾值去噪；隨著噪聲強度增加，二者的信噪比會有所下降，均方差有所增加，但本文方法仍優于小波閾值去噪。另外從圖3c）可以發現，采用小波閾值去噪雖然能夠去除隨機噪聲，但基線漂移無法消除，而本文算法不僅能夠很好地抑制隨機噪聲，基線漂移也得到很好地校正。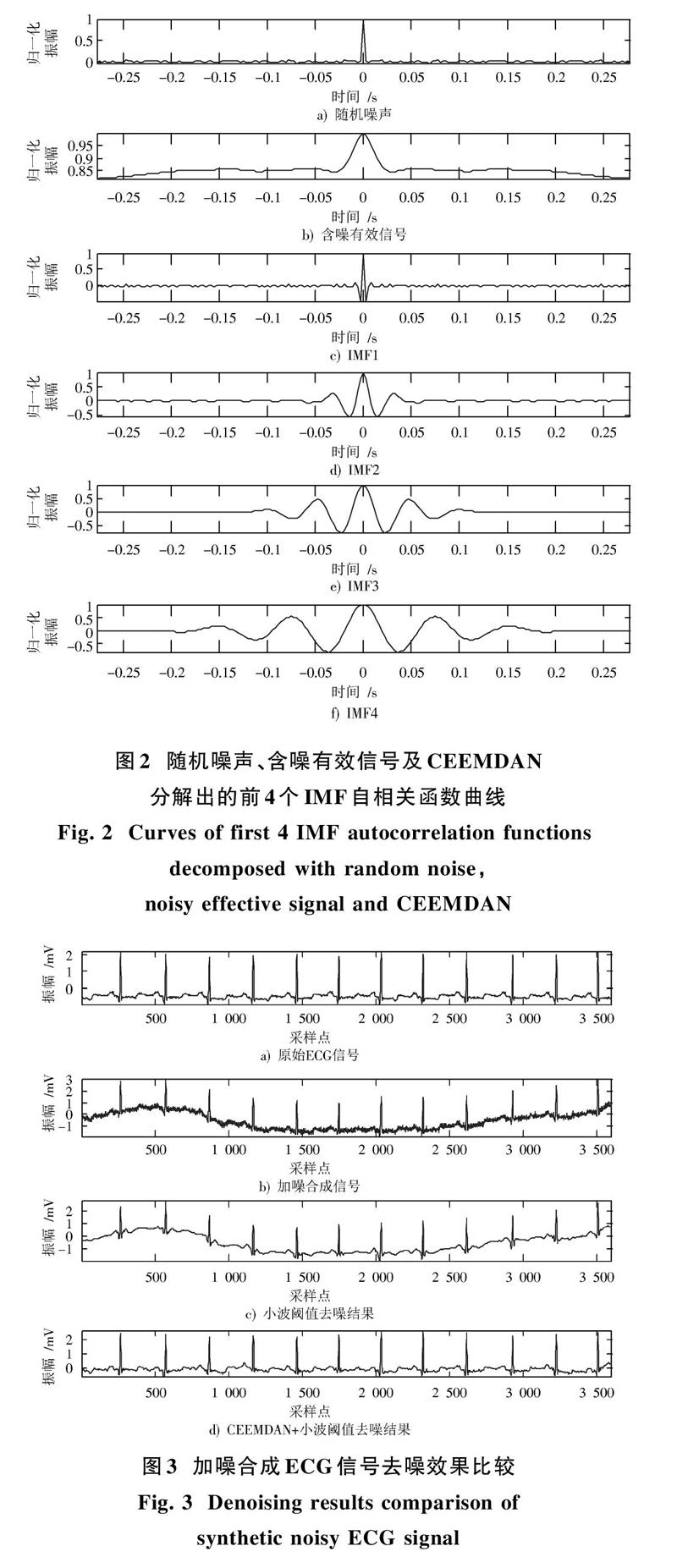

3.2 真實ECG信號去噪

從MIT?BIH標準心電數據庫中取得104號ECG原始數據（V5導聯，采樣頻率為360 Hz，采樣時間為10 s），選取其中一段受到較為嚴重隨機噪聲干擾并且具有基線漂移的數據，如圖4a）所示。

分別直接采用小波閾值算法和本文提出的CEEMDAN+小波閾值算法對該ECG數據進行去噪處理，小波閾值部分仍采用sym8小波基、啟發式軟閾值分解5層，去噪結果如圖4b）、圖4c）所示。從圖4b）中可以看出，直接采用小波閾值算法可以抑制大部分隨機噪聲，但基線漂移無法消除，從圖4c）中可以看出，采用本文算法既能獲得很好的隨機噪聲抑制效果，同時還可以有效消除真實ECG信號中的基線漂移。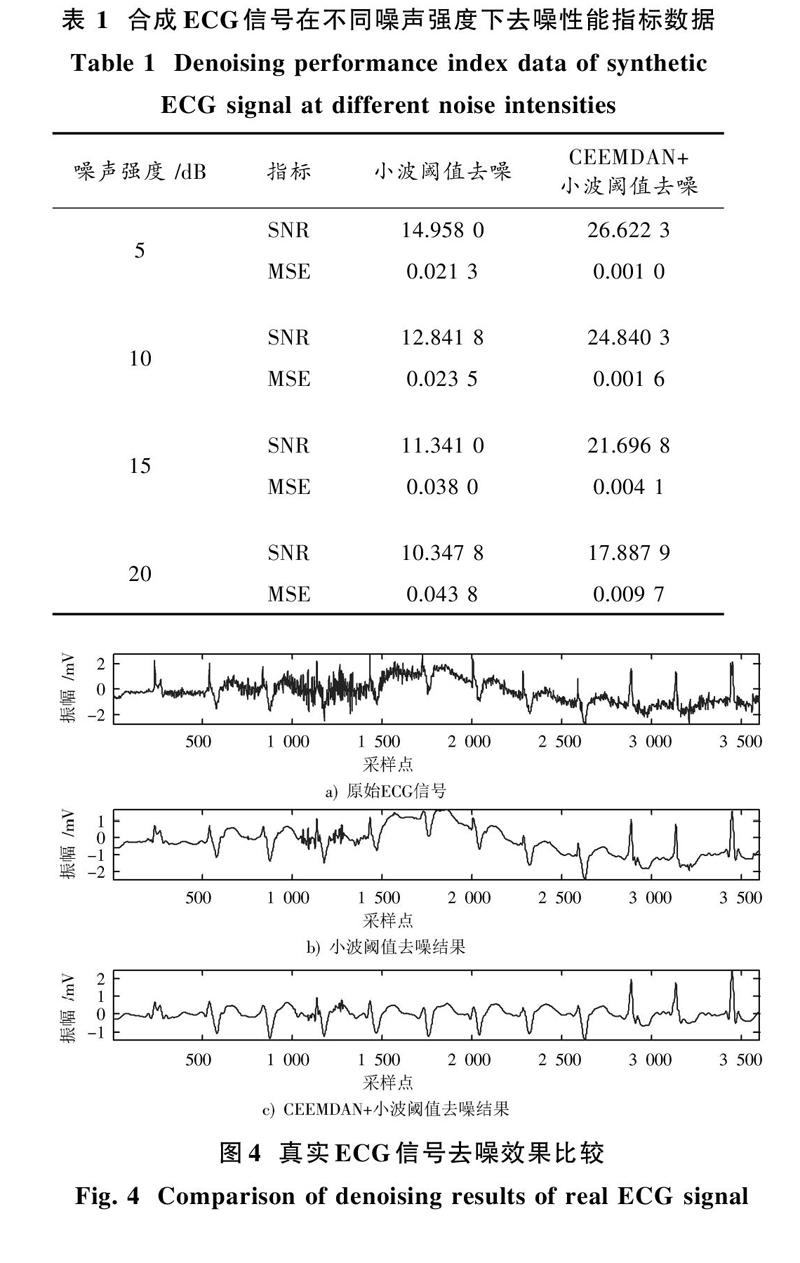

4 結 論

本文將自適應噪聲完備集合經驗模態分解（CEEMDAN）與小波閾值去噪相結合，提出一種新的ECG信號去噪算法。通過自相關分析來判定需要進行小波閾值去噪的高頻IMF分量，通過統計IMF分量的過零率確定需要剔除的基線漂移信號，最后進行IMF分量合并重構，達到抑制ECG信號中隨機噪聲和校正基線漂移的目的。采用本文算法對MIT?BIH標準心電數據庫的ECG信號進行去噪處理，無論是加噪合成信號還是真實信號都取得了較為理想的去噪效果，從而可以得出本文算法不僅能很好地抑制ECG信號中的隨機噪聲，同時具有良好的基線漂移校正效果。

注：本文通訊作者為羅明璋。

參考文獻

[1] TORRES M E， COLOMINAS M A， SCHLOTTHAUER G， et al. A complete ensemble empirical mode decomposition with adaptive noise [C]// Proceedings of 2011 IEEE International Conference on Acoustics， Speech and Signal Processing. Prague： IEEE， 2011： 4144?4147.

[2] HUANG N E， SHEN Z， LONG S R， et al. The empirical mode decomposition method and the Hilbert spectrum for non?stationary time series analysis [J]. Proceedings of mathematical physical & engineering sciences， 1998， 454： 903?995.

[3] MALLAT S. A wavelet tour of signal processing [M]. San Diego： Academic Press， 1998.

[4] DONOHO D L. De?noising by soft?thresholding [J]. IEEE tran?sactions on information theory， 1995， 41（3）： 613?627.

[5] TO A C， MOORE J R， GLASER S D. Wavelet denoising techniqures with applivations to experimental geophysical data [J]. Signal processing， 2009， 89（4）： 144?160.

[6] 王姣，李振春，王德營.基于CEEMD的地震數據小波閾值去噪方法研究[J].石油物探，2014，53（2）：164?172.

WANG Jiao， LI Zhenchun， WANG deying. A method for wavelet threshold denoising of sesmic data based on CEEMD [J]. Geophysical prospecting for petroleum， 2014， 53（2）： 164?172.

[7] 王婷.EMD算法研究及其在信號去噪中的應用[D].哈爾濱：哈爾濱工程大學，2010.

WANG Ting. Research on EMD algorithm and its application in signal denoising [D]. Harbin： Harbin Engineering University， 2010.

[8] 李軍，李青.基于CEEMDAN?排列熵和泄漏積分ESN的中期電力負荷預測研究[J].電機與控制學報，2015，19（8）：70?80.

LI Jun， LI Qing. Medium term electricity load forecasting based on CEEMDAN?permutation entropy and ESN with leaky integrator neurons [J]. Electric machines and control， 2015， 19（8）： 70?80.

[9] HUANG Weiwei， CAI Nian， XIE Wei， et al. ECG baseline wander correction based on ensemble empirical mode decomposition with complementary adaptive noise [J]. Journal of medical imaging and health informatics， 2015， 5： 1?4.

[10] AGRAWAL S， GUPTA A. Fractal and EMD based removal of baseline wander and powerline interference from ECG signals [J]. Computers in biology and medicine， 2013， 43（11）： 1889?1899.

[11] 赫彬，張雅婷，白艷萍.基于ICA?CEEMD小波閾值的傳感器信號去噪[J].振動與沖擊，2017，36（4）：226?231.

HE Bin， ZHANG Yating， BAI Yanping. A method for sensor signal de?noising based on ICA?CEEMD wavelet threshold [J]. Journal of vibration and shock， 2017， 36（4）： 226?231.