預應力結構模態參數數值模擬與試驗差異分析

王國杰，季家威，常軍

(蘇州科技大學土木工程學院，江蘇蘇州215011)

0 引言

預應力結構應用范圍非常廣泛。在建筑工程中，預應力技術是建造大跨度、大開間結構的重要技術，也是建造高層和轉換層等承受特種荷載結構的關鍵技術。在公路工程中，預應力技術是解決路面混凝土開裂的有效手段[1]。在橋梁和隧道工程中，由于預應力結構有利于承受動荷載，可以充分利用高強材料減輕結構自重[2]，自20世紀50年代以來，我國絕大部分大型橋梁使用了預應力混凝土結構。目前我國在役的預應力混凝土橋梁，由于混凝土徐變以及預應力筋松弛等原因普遍存在較大的預應力損失，嚴重影響結構的正常工作。故評估結構的有效預應力是預應力橋梁檢測的重要部分[3]。已有的檢測預應力損失的技術，如鋼筋應力緩釋孔技術(SSRHT)、形狀記憶合金技術等，為有損檢測方法，對結構不利。無損檢測技術，如聲發射技術等的識別精度有待于進一步提高[4]。而基于結構自振頻率的動力檢測技術則能有效避免上述不足[5]。

國內外許多專家學者在預應力結構的模態分析領域取得了一定的成果[6]。Saiidi、李瑞鴿、劉齡嘉等[7-10]通過試驗證明混凝土簡支梁的自振頻率隨著預應力值的增大而增大，這種變化趨勢與理論計算有差異，導致通過結構模態參數識別結構的有效預應力存在困難。為了建立結構模態參數與預應力結構損傷的精確關系，進而采用結構模態參數識別預應力損失，本文引入結構非線性，研究預應力結構模態參數的數值模擬和試驗研究結果的差異性。

1 考慮幾何非線性的預應力結構數值分析

1.1 非線性分析理論

ABAQUS有限元軟件采用Newton迭代法、修正的Newton迭代法、Quasi-Newton法作為求解非線性平衡方程的數值方法。

線性分析是指施加的荷載與結構的響應之間為線性關系，即荷載增量df與位移增量dx的比值為常數。在線性有限元分析中，結構的柔度矩陣只需要求解一次，剛度矩陣只需要對柔度矩陣求逆，所以結構的剛度矩陣是始終不變的。

在工程計算中，線性分析只是為了計算方便，在滿足計算精度的情況下對非線性行為進行近似。非線性結構的剛度是隨著結構的變形而變化的，非線性系統的響應不是施加荷載的線性函數，結構的響應不能再通過初始柔度矩陣乘以施加的荷載來計算，結構的剛度矩陣在分析過程中需要進行多次迭代，每一次迭代都伴隨剛度矩陣的變化。非線性分為幾何非線性、材料非線性[11]和邊界條件非線性。只要位移的大小影響到結構的響應就會發生幾何非線性。結構發生大的撓度或轉動、突然翻轉、受到初始應力或荷載加強都會發生幾何非線性[12]。鑒于鋼梁材料的各向同性，故本文基于幾何非線性研究鋼梁的模態問題。

1.2 有限元模態分析理論

有限元軟件ABAQUS是在線性攝動(linear perturbation)的頻率分析步中進行結構的模態分析，分析采用式(1)的自由振動方程：

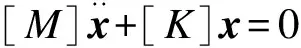
(1)

式中:x表示位移向量;[M]為質量矩陣;[K]為剛度矩陣。

運用ABAQUS軟件進行模態分析時，將考慮預載引起的初始應力和荷載剛度效應，并在基態(base state)增量步繼承上一分析步結束時的剛度矩陣，這為預應力結構的模態分析提供了條件。在預應力結構的特征值提取過程中，頻率分析步是線性分析步，所有的外荷載、阻尼等非線性特性都會被忽略。雖然在頻率分析步打開了幾何非線性選項，但整個特征值提取過程是線性過程，幾何非線性作為分析的初始條件只是在基態增量步被考慮進去，而基態的幾何非線性來自于考慮幾何非線性的上一分析步。

在ABAQUS頻率分析步中，結構的剛度都是基于初始狀態的剛度(即基態增量步的剛度)，若頻率分析步是第1個分析步，則結構的剛度就是基態增量步的剛度；若頻率分析步之前是通用靜力分析步，則基態增量步的剛度會繼承通用靜力分析步的最后1個增量步的剛度。詳細非線性迭代過程見圖1。

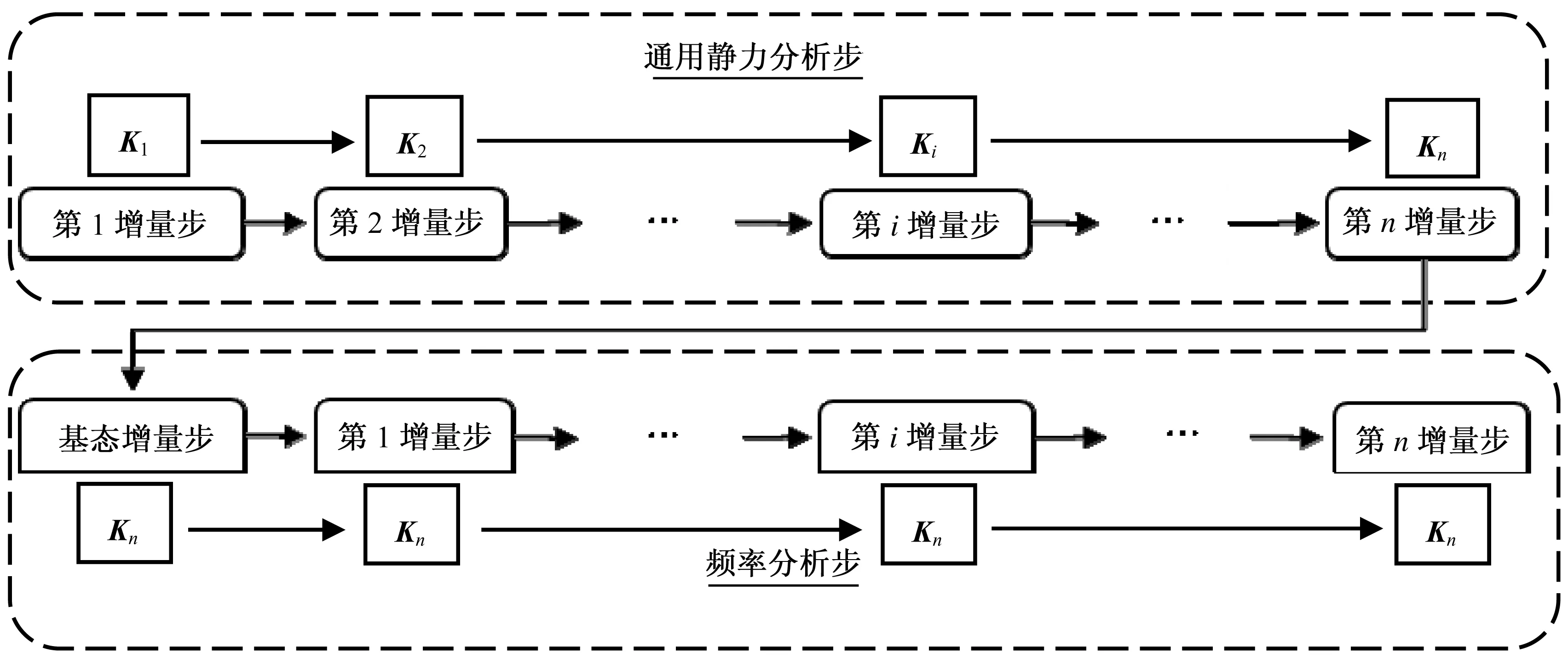
圖1 非線性迭代過程

由圖1可知，若第1個分析步(靜力分析步)是線性的，正如線性分析理論所述，在迭代過程中，其剛度矩陣不會發生變化并且始終為K1。若第1個分析步(靜力分析步)是非線性的，其剛度矩陣會隨著迭代過程發生變化，從第1增量步的剛度K1變化到第n增量步的剛度Kn，則第2個分析步(頻率分析步)的初始剛度繼承靜力分析步的最后1個增量步的剛度Kn，這樣第1個分析步的非線性迭代過程使整體分析過程變成了非線性模態分析過程。

故預應力結構的模態分析需要使用2個分析步，通用靜力分析步作為第1分析步用于施加預應力，頻率分析步作為第2分析步用于提取自振頻率。這樣就可分析預應力結構的自振頻率。

上述分析表明：模態描述的是結構在一定狀態下的振動情況，與外荷載無關，但外荷載是改變結構所處狀態的因素，當狀態改變時，結構的固有頻率也會隨之改變。故在對受初始應力的結構進行模態分析時，需要考慮初始應力對結構所處狀態的影響，即需要考慮初始應力對結構產生的初始變形。

1.3 理論分析模型

軸向力作用下各向同性材料的簡支梁會產生初始變形，設梁的運動符合彎曲變形的平截面假定,則梁的彎曲變形運動方程[13]為

(2)

式中:m表示分布質量;x為梁上某點到梁左端的長度;u為梁上某點的豎向位移;P為作用在梁上的外力;EI為梁的抗彎剛度;N為軸向力或預應力筋的拉力;t為時間。

根據簡支梁的邊界條件，求得考慮軸向力時簡支梁的自振頻率

(3)

式中：L為簡支梁的計算跨徑；n=1,2,…，∞。

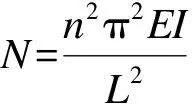
將式(3)寫成

(4)

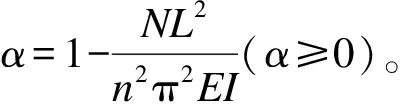
從式(4)可知，軸向力使結構剛度發生變化。N為軸向壓力且N小于屈曲荷載時，0≤α≤1，軸向力使結構剛度減小；N為軸向拉力時，α>1，軸向力使結構剛度變大。

綜上，軸向力作為一種初始應力改變了結構的初始幾何狀態，使結構產生了幾何非線性，同時導致結構剛度發生相應變化，最終使結構的模態參數發生相應變化。

2 預應力結構模態參數差異性分析

2.1 預應力簡支鋼梁的模態分析

本文選用王龍林[14]鋼梁試驗模型進行有限元模擬和理論計算的對比分析，鋼梁的試驗布置如圖2所示。

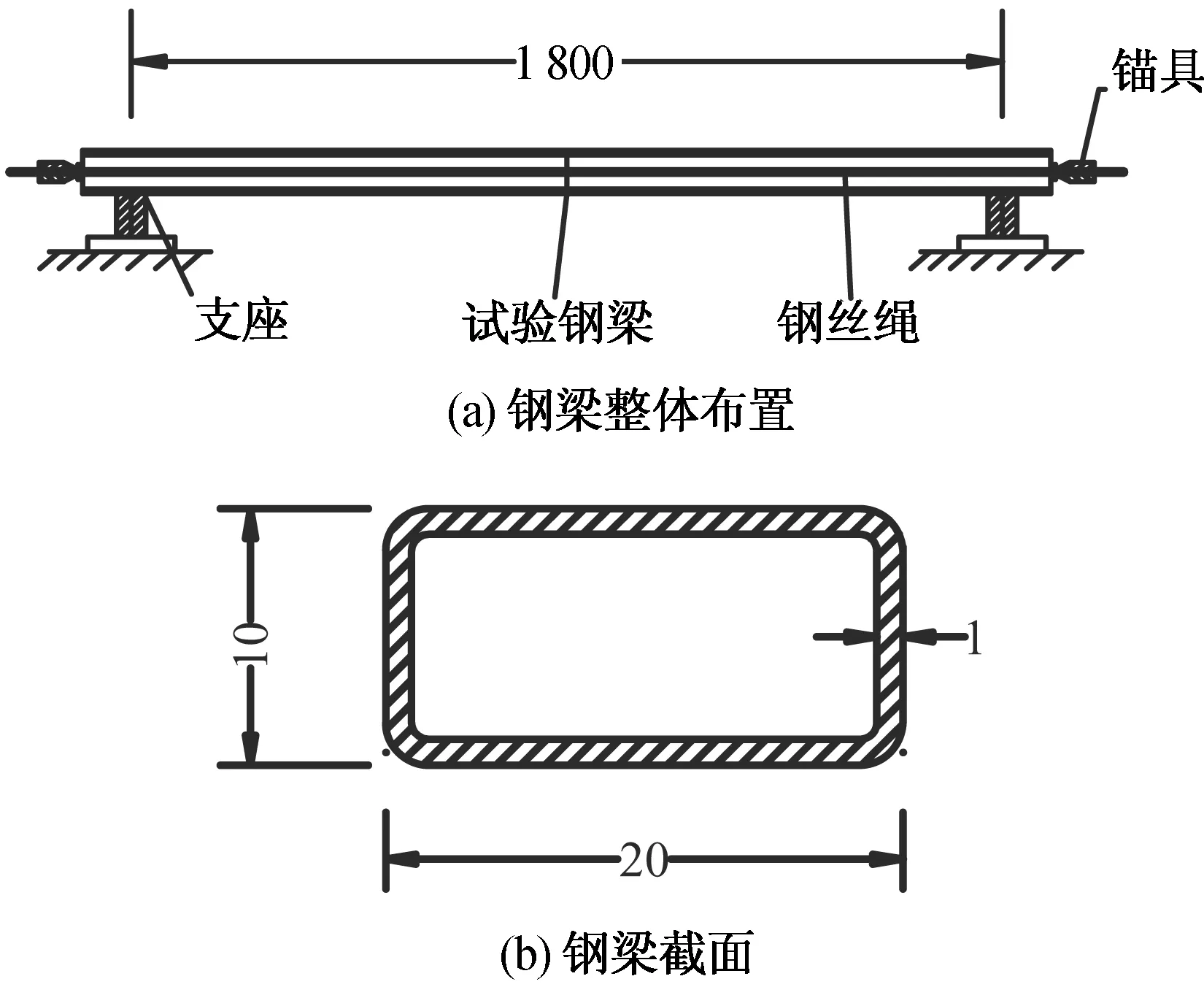
圖2 試驗布置圖(單位：mm)

為了方便進行有限元模擬及理論計算，忽略型鋼倒角。鋼梁計算跨徑為1 800 mm，型鋼截面為20 mm×10 mm的方管截面，管壁厚1 mm。鋼梁材料為Q235，彈性模量E=2.1×105MPa，鋼梁的密度ρ=7 850 kg/m3。通過計算得到結構關于橫軸的慣性矩Ix=898.667 mm4，橫截面積A=56 mm2，單位長度質量m=ρA=7.85×10-9×56 t/mm =4.396×10-7t/mm。由式(3)求得簡支鋼梁的自振頻率見表1。

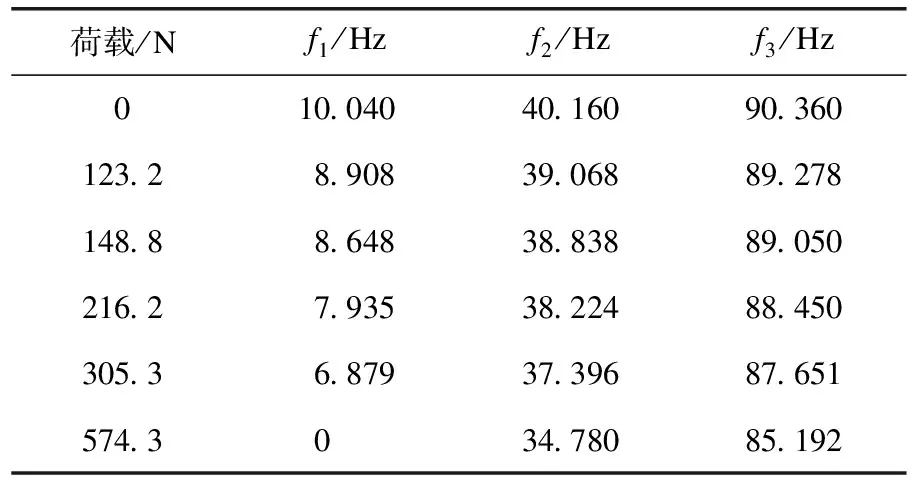
表1 各級荷載工況下結構自振頻率的理論值

利用ABAQUS有限元軟件進行建模，單元選擇B31梁單元，兩端鉸接，材料屬性與理論計算相同，在模型的兩端對結構施加軸向壓力來模擬預應力效應。有限元模型如圖3。

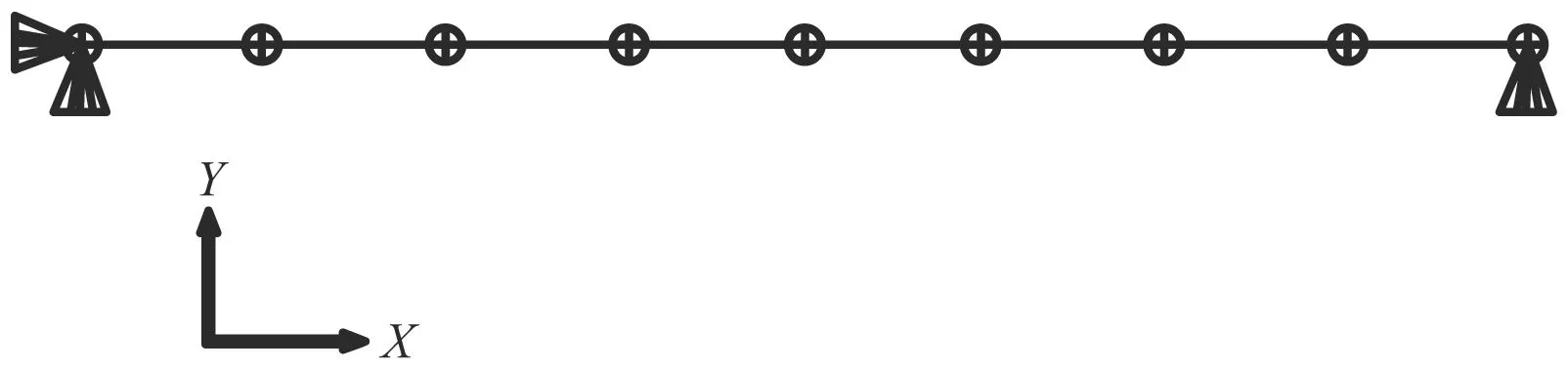
圖3 有限元模型

不考慮幾何非線性，施加不同等級的預應力，有限元分析結果顯示：結構的一、二、三階自振頻率分別為10.000、39.979、89.868 Hz。每一階自振頻率都不隨預應力大小的改變而變化。

考慮幾何非線性，施加不同等級的預應力，利用有限元軟件得到結構在不同荷載工況下的頻率響應，見表2。

表2 考慮幾何非線性結構自振頻率的有限元計算值

對比可知，不考慮幾何非線性，有限元分析結果與理論計算結果不符。考慮幾何非線性，有限元分析結果與理論計算結果基本一致：結構的各階自振頻率隨著預應力的增大而減小，特別地，預應力達到574.3 N時，結構發生屈曲失穩，導致結構的自振頻率為0。這說明考慮幾何非線性更能反映結構在初始應力狀態下的模態參數。

結合表1和表2，考慮幾何非線性，不同荷載工況下結構自振頻率的理論計算值、有限元計算值與試驗值的對比分析見表3。

計算結果顯示，預應力會使結構的自振頻率發生改變。雖然在148.8 N荷載工況下結構自振頻率的試驗值相對于前一工況有所增加，但整體上結構的自振頻率是隨著預應力的增大而減小。這說明，預應力改變了結構的初始幾何狀態，使結構產生了幾何非線性，導致結構的剛度減小，即預應力使鋼梁發生了“壓力軟化”效應[15]。

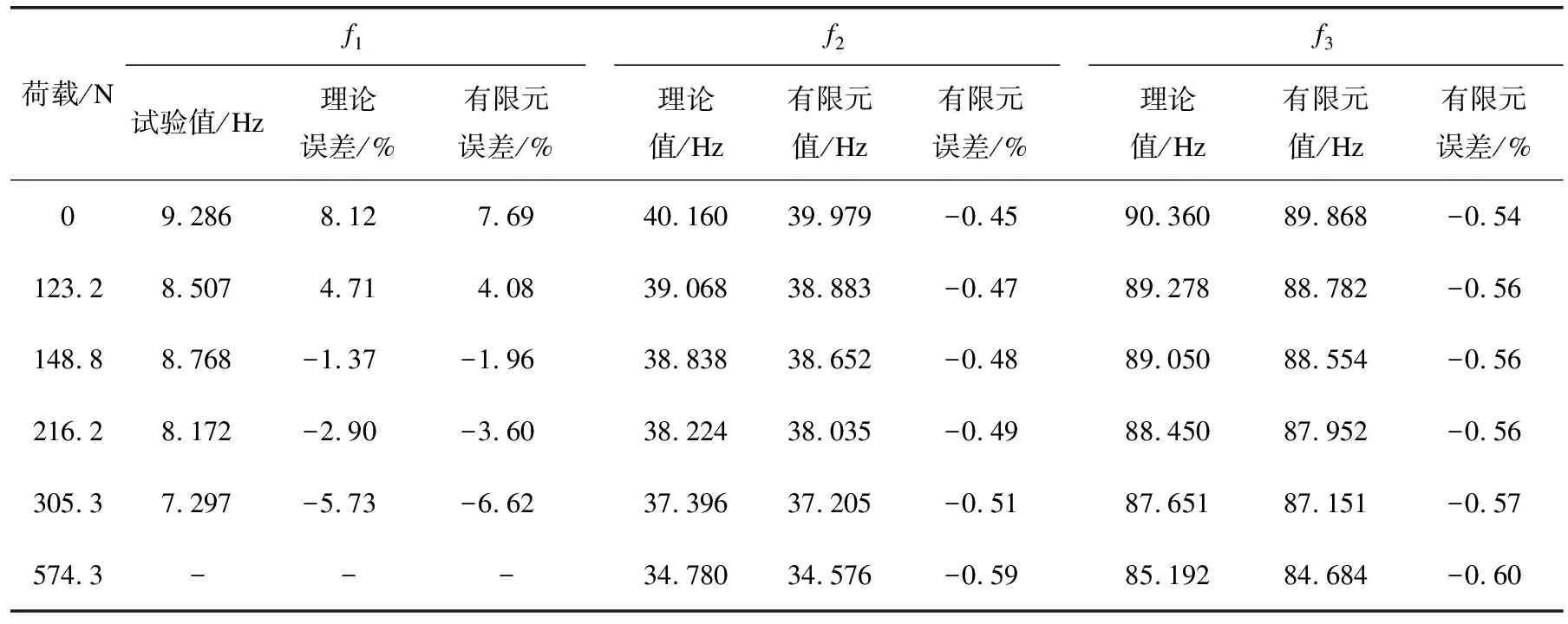
表3 考慮幾何非線性不同荷載工況下結構的自振頻率對比

注：①試驗值只有一階頻率值，試驗值取HHT變換結果中最小頻率與最大頻率的平均值。

②對于結構的一階頻率，以試驗值作為真實值。對于結構的二階頻率和三階頻率，以理論值作為真實值。

③荷載574.3 N為由式(2)計算得到的屈曲荷載值。

對于結構的一階頻率值，各個荷載工況下，理論計算值及有限元計算值與試驗值的誤差大小在1.37%～8.12%，除了第1個荷載工況誤差較大，其余工況誤差較小。誤差在可接受范圍內。造成上述誤差的原因是：1)在進行理論計算和有限元分析時，沒有對實際結構進行倒角處理，這相當于增大了截面，造成結構的剛度有所增大；2)存在不可避免的鋼梁制作誤差；3)理論計算及有限元模擬均忽略了結構的重力，實際結構在試驗中受到的豎直向下的重力對其自振頻率有一定影響。

2.2 預應力混凝土梁的模態分析

本文基于張耀庭的試驗研究[16]進行了數值模擬，并將數值模擬結果與試驗結果進行對比，以探究預應力對混凝土梁結構頻率的影響。試驗梁的截面尺寸為b×h=120 mm×240 mm,梁長為3 900 mm，計算長度為3 700 mm,混凝土標號為C40。采用1根7Φs5、1860級鋼絞線，其公稱截面面積為139 mm2。圖4為梁的構造示意圖。

混凝土采用C3D8R單元，鋼筋采用T3D2兩節點線性三維桁架單元，考慮分析過程中的幾何非線性，忽略材料非線性，預應力通過等效荷載法施加，采用有限元軟件建立結構的有限元模型見圖5。

有限元計算結果與試驗結果對比見表4。

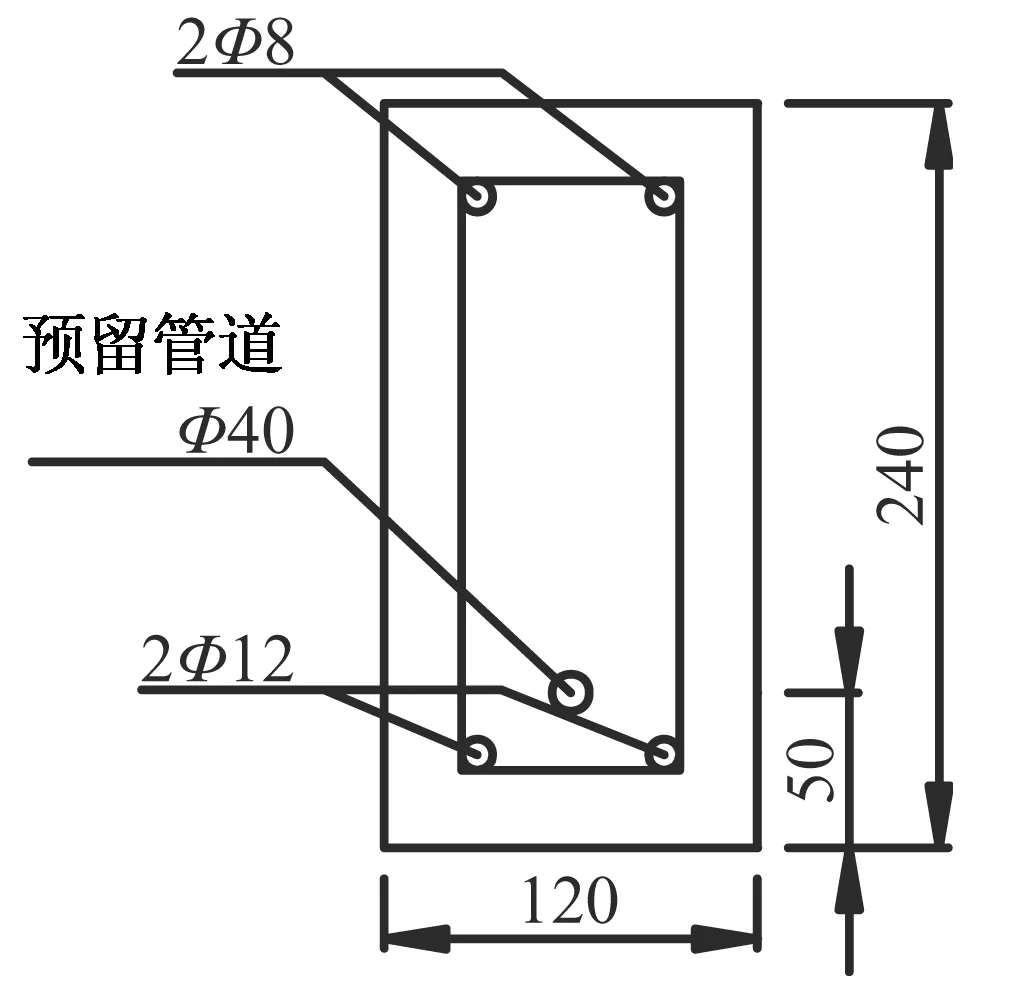
(a)梁截面圖

(b)梁構造示意圖圖4 梁構造示意圖(單位：mm)

圖5 試驗梁的有限元模型

當預應力由0 kN 增加到120 kN，對于試驗結果，梁的一階頻率值從28.36 Hz增大到29.80 Hz，

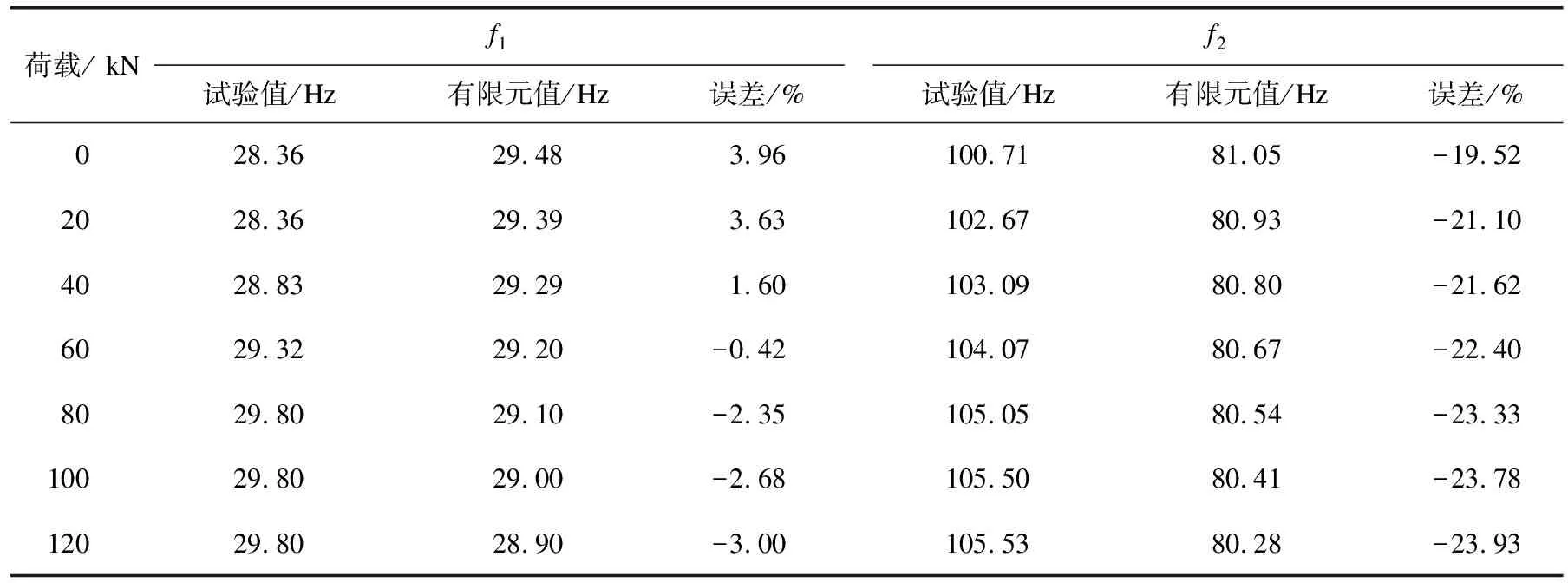
表4 有限元結果與實驗結果對比

即頻率增加了1.44 Hz；二階頻率值由100.71 Hz增大到105.53 Hz，即頻率增大了4.82 Hz。對有限元結果，一階頻率由29.48 Hz減小到28.90 Hz，即頻率減小了0.58 Hz；二階頻率由81.05 Hz減小至80.28 Hz，即頻率減小了0.77 Hz。總體來看，預應力簡支梁的自振頻率隨著預應力的變化趨勢，試驗結果與有限元模擬結果剛好相反。發生這種情況的原因是：實際結構中的混凝土材料是各向異性的，其內部會存在許多初始微裂縫，這些微裂縫會削弱混凝土梁的截面，即實際混凝土梁中都存在初始損傷。預應力的加載使得初始微裂縫逐漸愈合，結構的剛度也相應增大，表現為結構的各階固有頻率相應增大。

對于一階頻率值，有限元結果與試驗結果的誤差(最大誤差為3.96%)在可接受范圍內。對于二階頻率值，有限元結果與試驗結果的誤差較大，由于試驗環境的不確定性，此處誤差原因還有待進一步研究。

綜上，試驗中的預應力混凝土簡支梁存在幾何非線性與材料非線性，而有限元中只考慮了梁的幾何非線性，故試驗結果的頻率變化趨勢與有限元結果的頻率變化趨勢相反。材料非線性對結構剛度硬化的貢獻大于幾何非線性對結構剛度軟化的貢獻，在材料非線性與幾何非線性的綜合影響下，預應力混凝土梁表現為自振頻率隨著預應力的增大而增大。由于鋼梁材料是各向同性的，材料非線性對其模態參數的影響可以忽略不計，在理論計算與有限元模擬中，只考慮幾何非線性就能使結果與試驗結果吻合較好。

3 結語

簡支鋼梁的理論分析結果、有限元分析結果均表明，不考慮幾何非線性，無法反映結構在初始應力作用下的模態參數的變化；考慮幾何非線性，受軸向力作用的簡支鋼梁會發生“剛度軟化”效應，導致其各階的自振頻率減小，這與試驗結果一致。試驗結果表明，預應力混凝土簡支梁的固有頻率隨著預應力的增加而增大，即預應力的存在提高了結構的剛度，導致結構的固有頻率增大，但是僅考慮幾何非線性的有限元結果表明，預應力的存在導致結構的各階自振頻率減小。

對比簡支鋼梁和預應力混凝土梁得出：鋼材作為各向同性材料，在頻率分析中可以只考慮幾何非線性的影響，混凝土作為復雜的各向異性材料，其內部會存在微裂縫，在只考慮幾何非線性的情況下，其數值模擬結果與試驗結果相反，故對預應力混凝土結構進行模態分析，需要同時考慮幾何非線性與材料非線性的影響。

深入研究預應力與結構的固有頻率的定量關系，是利用結構的固有頻率變化識別結構有效預應力大小的基礎。本文基于幾何非線性探究了預應力與結構的固有頻率的關系，但由于在有限元計算中未考慮混凝土的材料非線性，導致頻率變化趨勢與試驗相反。故選擇合理的材料性能參數，充分考慮混凝土的材料非線性，將是后續工作中需要進一步研究的問題。