金剛石帶鋸機機架的模態和諧響應分析

彭少波，向小宇，陳 超，秦建新，陳家榮

(1.中國有色桂林礦產地質研究院有限公司,廣西超硬材料重點實驗室,國家特種礦物材料工程技術研究中心,桂林 541004；2.桂林航天工業學院, 桂林 541004)

0 前言

金剛石帶鋸機是一種特殊的切割設備，利用超薄的鋼帶，在鋼帶的邊緣側鍍上一層金剛石，用于切割硬脆性材料。在陶瓷、寶石等加工領域，對金剛石帶鋸加工的質量要求相當高，表面粗糙度、平面度和壽命是主要的衡量指標。為了滿足這些加工要求，鋼帶加工過程中要保持良好的穩定性。首先帶鋸機的機架本身的機構設計要合理，避免產生共振，而電機旋轉帶來的振動是主要的振動來源。在呂廷的文獻中[1]，為了避免共振產生較大的振動，對機架進行模態分析和諧響應分析，可以為后續電機選型以及切割速度的設計提供重要的理論依據。

本文首先利用SolidWorks軟件建立金剛石帶鋸機機架的三維模型，然后將模型導入workbench中進行模態分析，最后再進行諧響應分析。可以將電機周期的振源簡化成簡諧載荷，最終，求出低階的共振頻率和振幅，以及在外界簡諧振源下的響應[2]。

1 有限元模態分析基本理論

在動力學分析中，通用的運動方程為：

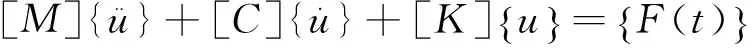
(1)

對于模態分析，機構假定為自由振動并忽略阻尼，結構的固有模態由結構本身的特性和材料特性決定，與外載荷無關；而結構阻尼對固有頻率的影響很小，可以忽略[3]，所以簡化為：

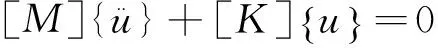
(2)

當發生諧振動，即u=Usin(ωt)，方程為：

(3)

故對于一個機構的模態分析，其固有圓周頻率ωi和振型φi都能從上面矩陣方程式中得到。這個方程的根ωi2，即特征值；i的范圍從1到自由度的數目，相應的向量是{u}i，即特征向量。特征值的平方根是ωi，它就是機構的自然圓周率(弧度/秒)，進而可得出自然頻率fi=ωi/2π(圈/秒)。特征向量{u}i表示振型，即假定機構以頻率fi振動時的形狀。模態提取只是用來描繪特征值和特征向量計算的術語，但在Mechanical模塊中求解上述方程式是在一定的假設條件下求解的，即[K]和[M]都是常量，且假設材料為線彈性材料，使用小饒度理論，還不包含非線性特性，不包含阻尼，也沒有激勵。

2 機架的模態分析

2.1 實體模型的建立

隨著workbench的應用日益廣泛，其需要處理的模型也越來越復雜，ANSYS白帶的建模功能顯示出很多的不足之處。SolidWorks作為一款三維CAD軟件，擁有強大的參數化建模能力，可以建立非常復雜的實體模型。基于兩個軟件之間的無縫連接屬性，我們充分利用SolidWorks快速準確建模的特點，把在SolidWorks中建立好的模型導入到Workbench中進行分析，有效提高了模型質量，簡化了分析工作[4]。

在利用SolidWorks軟件建立模型時，需要注意幾點，模型需要簡化，安裝的螺紋孔以及不重要的倒角可以忽略，保持實體特征的獨立性[5]。

2.2 有限元模型的建立及模態分析

將在SolidWorks中建立的三維模型按默認方式直接保存為“SLDPRT”格式，在Workbench的實體選擇時直接調用。

然后定義材料參數，機架由多塊Q235鋼板焊接組成，可以直接調用結構鋼參數，彈性模量為200GPa，泊松比為0.3，密度為7.86kg/m3。

劃分網格。本文選擇自動劃分法，實際是在四面體與掃掠型劃分之間自動切換，幾何體不規則時，自動生成四面體網格，幾何體規則時，自動生成六面體網格。

設置邊界條件。由于機架工作時，不受外力的作用，不需要添加預緊力，通過螺栓將機架底部固定在底座上，需要將機架底面設置成全部約束。

求解。機架本身結構剛度較大，外界的激勵頻率較小，只需求解前六階的共振頻率即可滿足設計要求。對廣義特征值問題，軟件中提供了7種求解方法[5]：Block lanczos(分塊的蘭索斯)法、Subspace(子空間)法、Power Dynamics(動力學)法、Reduced(縮減)法、Unsymmetric(非對稱)法、Damped(阻尼)法、QR(阻尼)法，最后一種方法允許結構中包含阻尼。本文中選用了適用于求解大型對稱特征值的分塊蘭索斯法(Block Lanczos)，相比其他方法，其具有求解精度高、收斂速度快的優點。

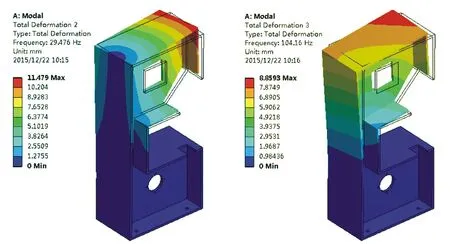
圖1 一階振型圖2 二階振型Fig.1 First-ordermodeFig.2 Second-ordermode

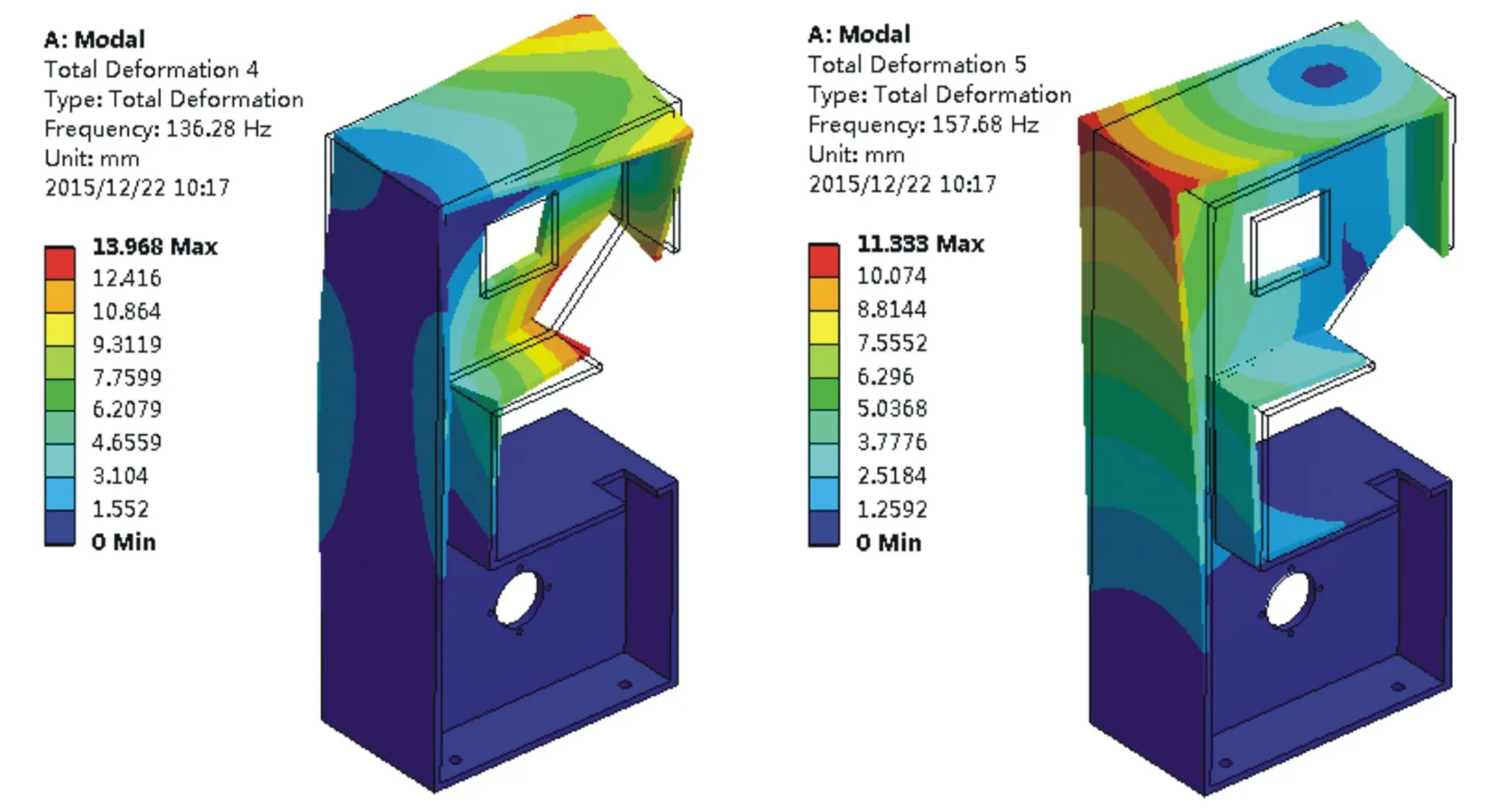
圖3 三階振型圖4 四階振型Fig.3 Third-ordermodeFig.4 Forth-ordermode

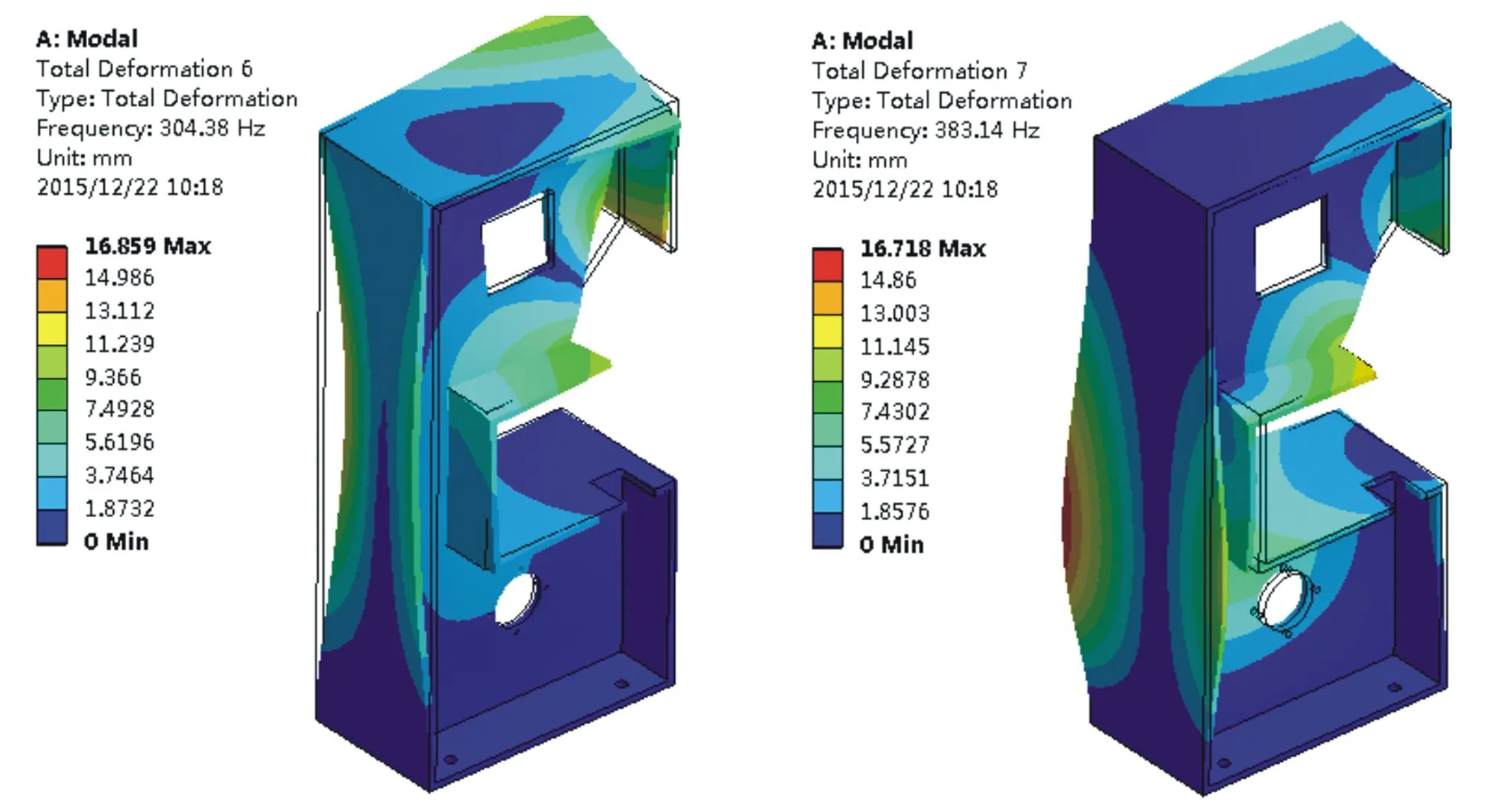
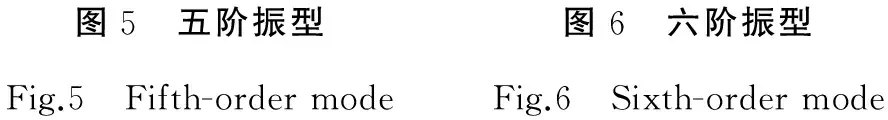
圖5 五階振型圖6 六階振型Fig.5 Fifth-ordermodeFig.6 Sixth-ordermode

前六階振型如圖1至圖6所示，通過一至六階振型分析可得知，機架的下部分固定在底座上，下部剛性大，產生的振動小，由于上部分成懸空狀態，機床的薄弱環節在機床上身部分。

機架前六階的共振頻率和振幅描述如表1所示，機床工作狀態下[6]，激振主要來自于電機轉動等原因，求出電機的最大轉動頻率為93 Hz，大于機床一階共振頻率29.47Hz且靠近二階共振頻率104.16 Hz。所以，帶鋸機在設計時，考慮到共振的因素，應該適當降低常用速度，取一階和二階共振頻率之間，約為75Hz，換算的電機轉速為1125(轉/分鐘)。

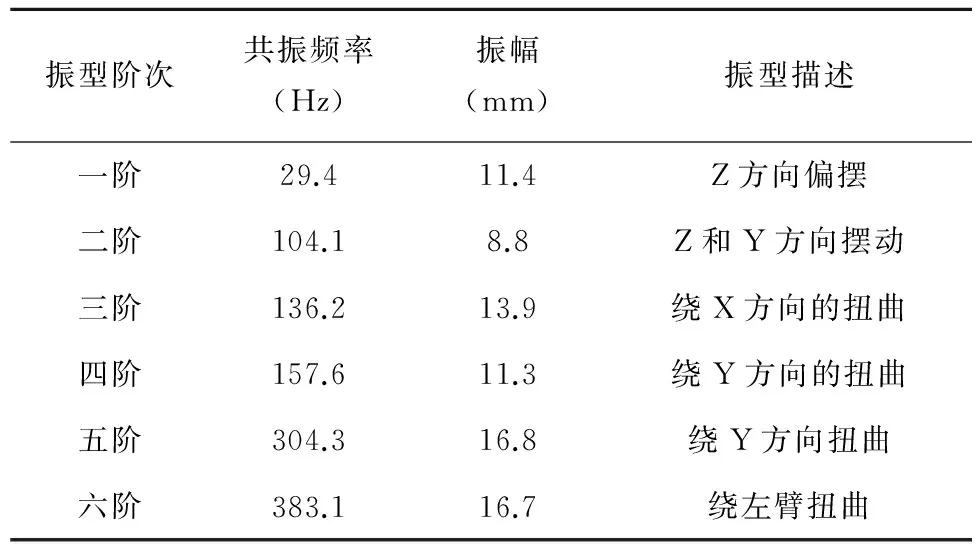
表1 初始狀態機架模態分析結果

3 機架的結構與邊界條件影響

3.1 添加加強筋

通過前面的模態分析，帶鋸機機架安裝在一個沉重的底座上，可以認為是一個固定不動的物體，所以模擬分析時對帶鋸機機架的底面設置全約束。為了能改變機架的共振頻率，本文在此處設計一些局部的強化剛體結構。機架上部類似懸臂梁，剛性較差容易振動，本文在此添加加強筋用以增強懸掛結構的剛度。經過修改后的機架，再進行相同條件下的模態分析，得出它的前六階共振頻率，見表2所示。

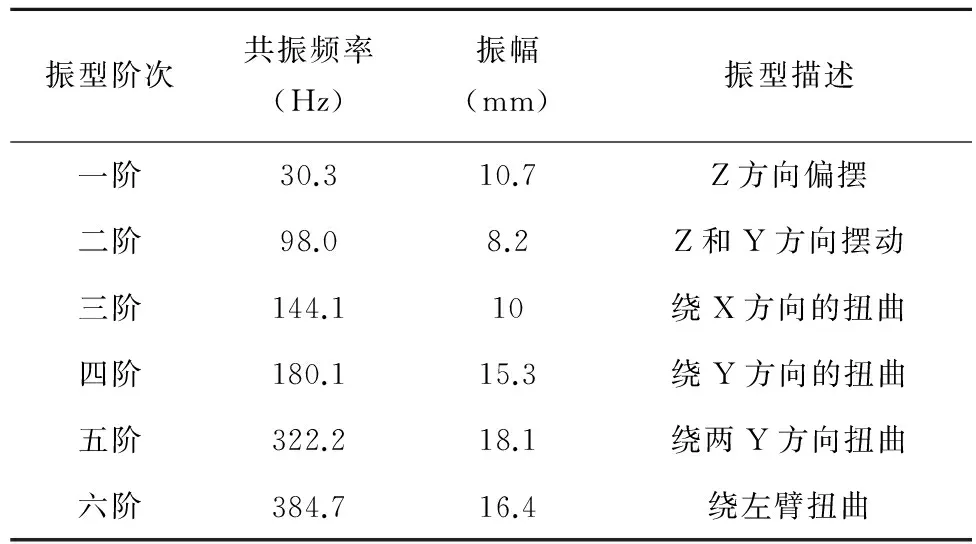
表2 增加加強筋的機架模態分析結果

添加加強筋之后，機架的一階振型如圖7所示.經過與優化前的分析比較得出，機架的共振頻率基本不變，振幅有所減少，振型基本一致，表明加強筋對機架的共振頻率影響較小。因為，加強筋在整個結構中的質量比例很小，而且結構的形狀沒有發生變化，整體類似一個“E”字。

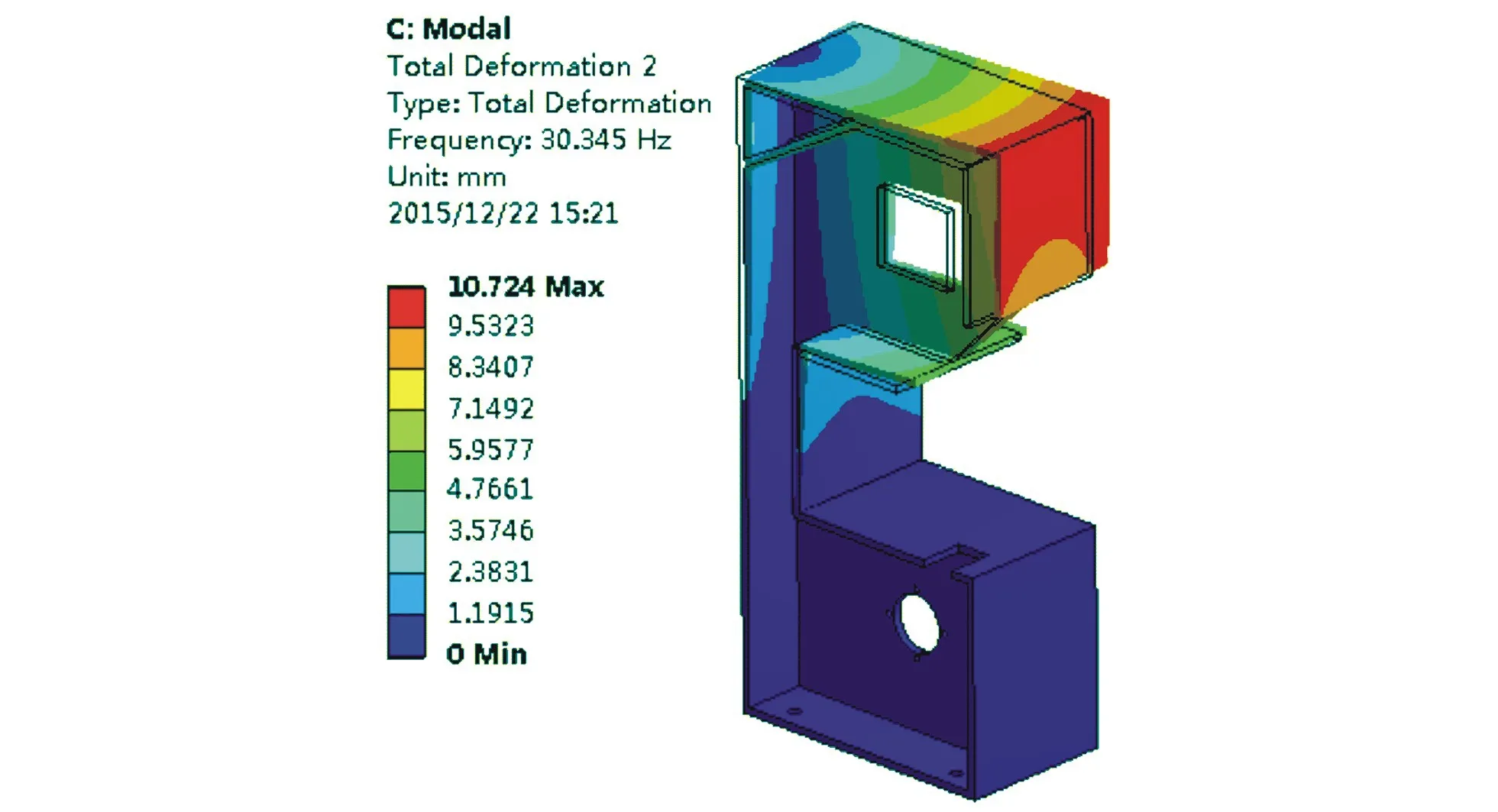
圖7 優化后機架的一階振型Fig.7 First-order mode after optimization

實際設計中，為滿足使用要求，機架的結構必須設計成中間開口的形式，騰出空間用作加工工件的通行通道。基于這種框架，如果只希望通過一些局部的加強設計，則難以對改變共振頻率產生大的作用。

3.2 改變邊界條件

從對上述增設加強筋之后的模態分析可知，加強筋對機架的共振頻率影響較小，基本可以忽略，改變加強筋的位置或者再增加其他的加強筋，對整體的共振頻率而言，不會帶來較大的變化。在此，希望通過改變它的邊界約束條件來改變它的共振頻率。實際設計時，可以在底面和左側面同時進行固定約束，側面的固定約束可以大大增加機架上部的剛性。基于初始條件，只增加側面的約束條件，在其他條件不變的情況下，進行模態分析。增加邊界約束之后，機架一至六階的振型如圖8至圖13所示，共振頻率及振幅描述如表3所示。通過表3的數據和一至六階振型圖可知，機架的一至六階共振頻率都有大幅的提高，一至六階的振型描述也都有較大的變化。

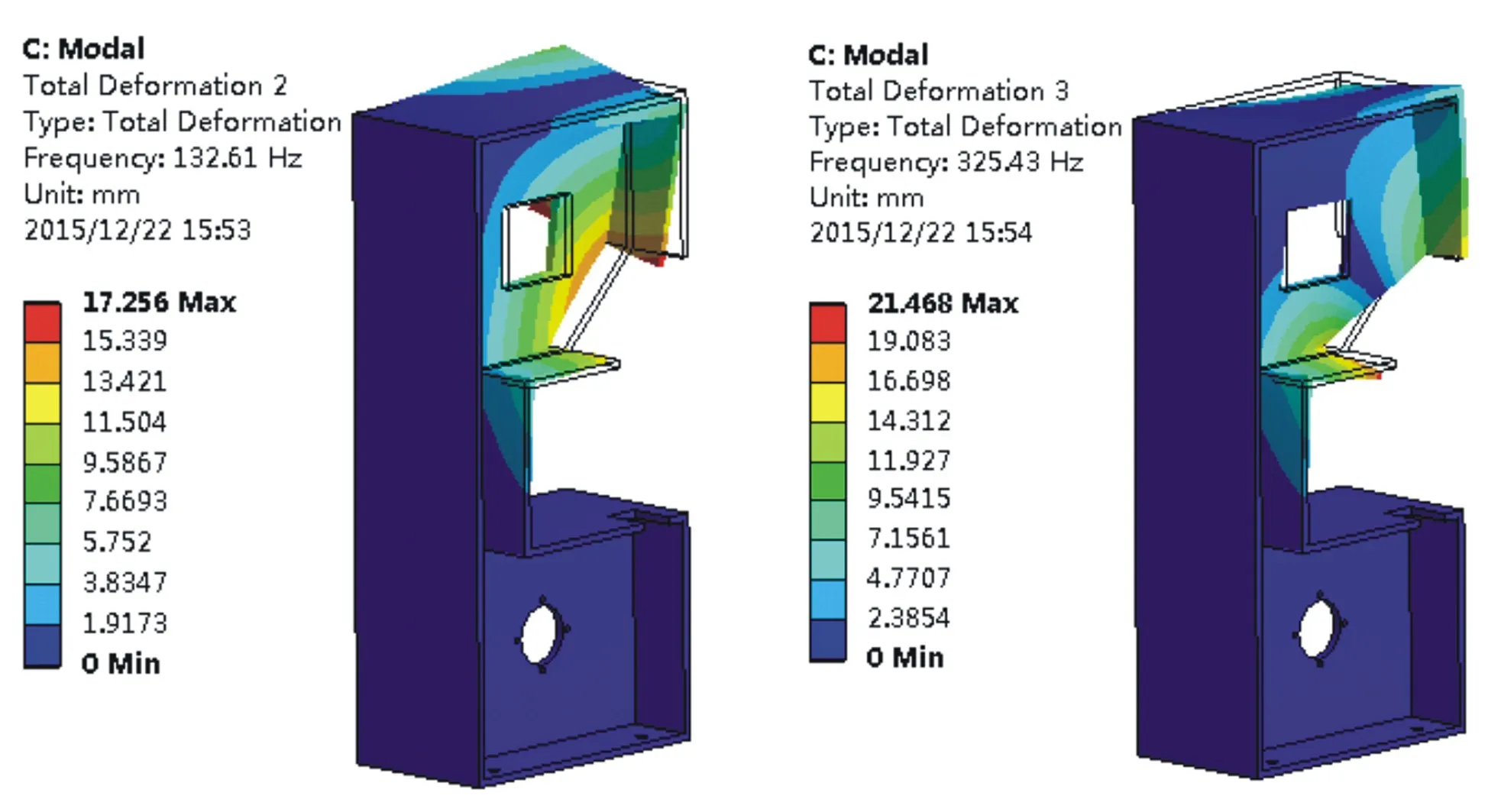
圖8 一階振型圖9 二階振型Fig.8 First-ordermodeFig.9 Second-ordermode

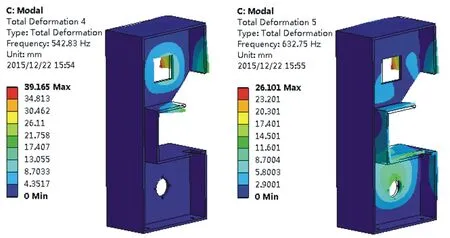
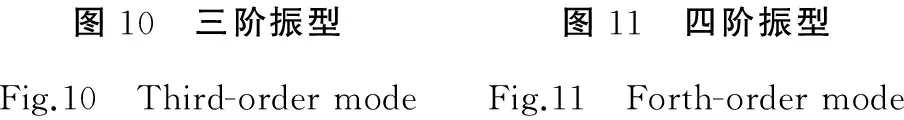
圖10 三階振型圖11 四階振型Fig.10 Third-ordermodeFig.11 Forth-ordermode

圖12 五階振型圖13 六階振型Fig.12 Fifth-ordermodeFig.13 Sixth-ordermode

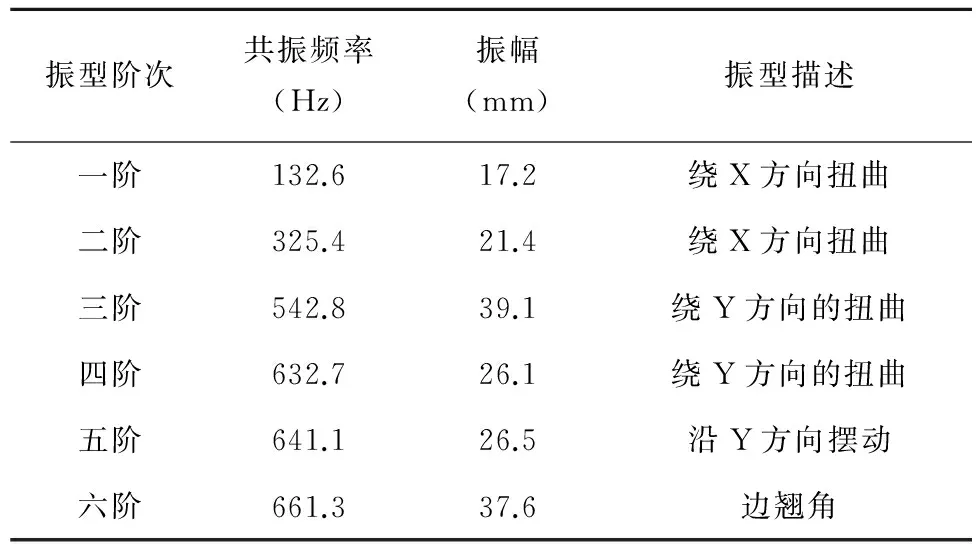
表3 改變邊界約束機架模態分析結果

如圖14所示，三條曲線代表初始狀態、增加加強筋和增加約束三種狀態下一至六階的共振頻率曲線。

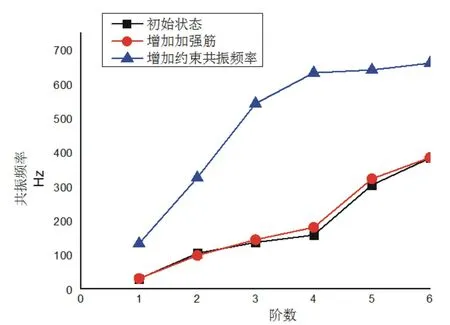
圖14 共振頻率曲線圖Fig.14 Resonance frequency curve

通過圖14的比較可知，相比前兩種狀態，單一改變機架的邊界約束條件時，機架的一至六階共振頻率都有較大的增加。而且所有的共振頻率都高于電機產生的振動頻率，完全避開了電機的最大振動頻率，如此，電機的轉數可以任意設置，不會對機架共振產生影響，為整機的速度設置提供了良好的選擇依據。

4 諧響應分析

經過之前的模態分析，改變邊界約束條件較為適合，基于機架的一階共振頻率為132.61Hz，電機最大的振動頻率為93Hz，與一階共振頻率最接近，以最大的振動頻率作為激勵源進行諧響應分析，模擬仿真求得的響應振型如圖15所示。

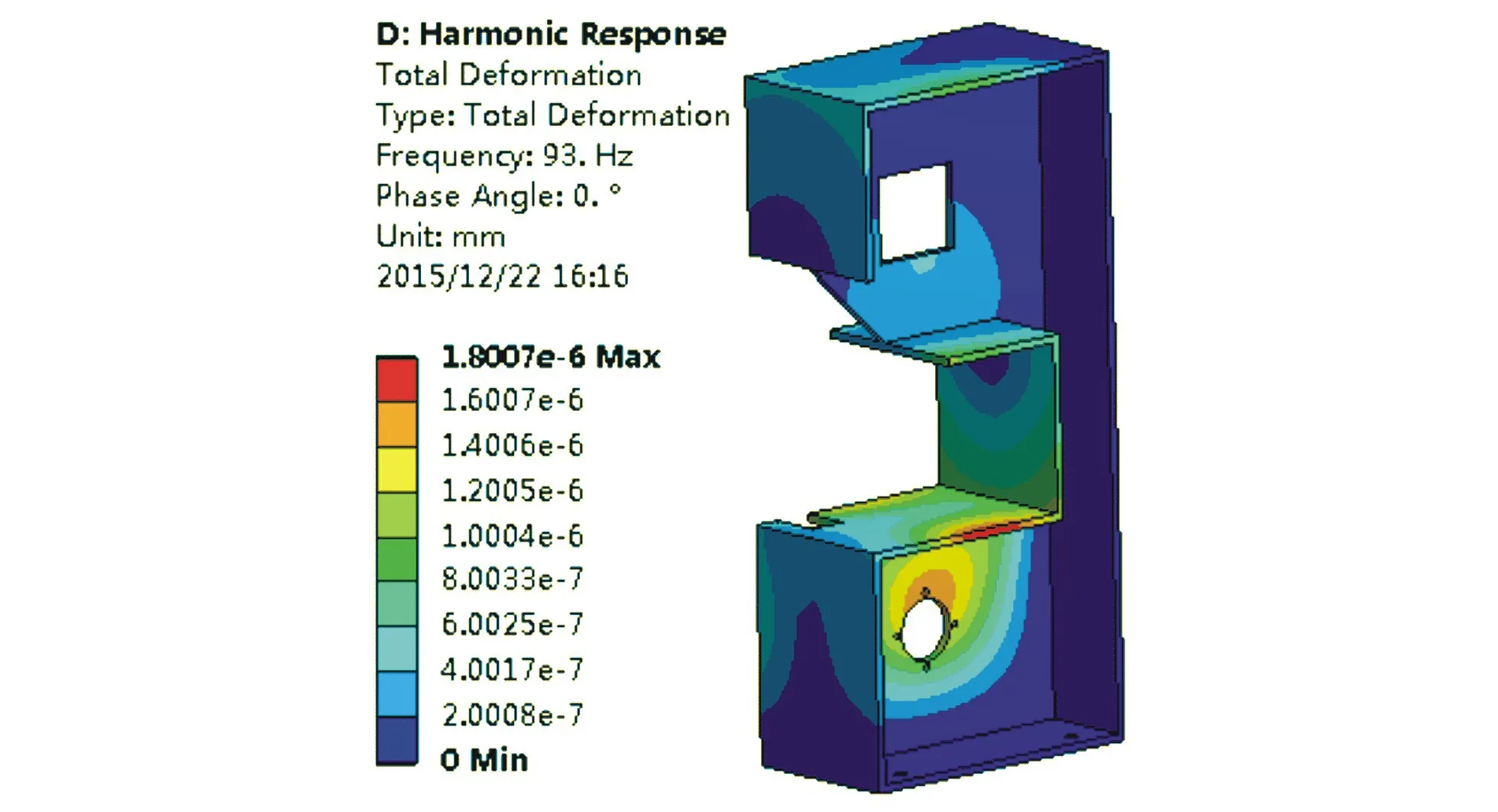
圖15 諧響應分析振型Fig.15 The modal of harmonic response analysis

最大振幅處于機架的下端，合成振幅為1.8×10-6mm，相對于加工精度的要求比較，這個振動的

影響可以忽略不計。整機設計時，帶鋸機機架在X方向的振動對切割的質量影響最大，分析得出X方向的諧響應分析的振幅為1.28×10-7mm，可知X方向的振動影響更加微小，可以忽略不計。綜上所述，帶鋸機機架的結構在設計時增加側面的約束，可以大大提高共振頻率，從而避開電機帶來的頻率范圍，將產生共振的影響降至最低，從而提高整個帶鋸機的穩定性。

5 結論

(1)利用Workbench軟件對機架進行了模態分析，初始狀態下機架的一階共振頻率較小，在電機振動源的頻率范圍內，通過增加邊界約束條件的改進之后，一階共振頻率大幅提高，可以避開共振頻率范圍。

(2)以電機振動產生的最大頻率作為激勵頻率，進行諧響應分析，得出最大的振幅位置和振幅值。由于振幅值較小，相對于加工精度的要求，可以忽略不計。說明改變邊界約束條件的方案可行，能滿足設計要求，為設計提供了一定的依據。

[1] 呂廷，石秀東，張秋菊，等.基于ANSYS的破碎機機架模態分析[J].機械設計與制造，2008(11)：99-101.

[2] 劉昌領，羅曉蘭.基于ANSYS的六缸壓縮機連桿模態分析及諧響應分析[J].機械設計及制造，2013(3):26-29.

[3] 石廣豐，倪坤，史國權，等.基于ANSYS workbench的激光打孔機模態分析[J].長春理工大學學報，2010,33(4)：95-97.

[4] 宗坤，張宏洋，王建有，等．SolidWorks建模以及與ANSYS的接口問題探討[J]．中國農村水利水電，2007(9)：82-84.

[5] 徐春雨，陳剛，周淵鍵.基于SolidWorks和ANSYS某舵機齒輪裝配體模態分析[J].機械傳動，2012，36(04):81-83.

[6] 葉魯浩，王志，張進生，等.基于ANSYS圓鋸片模態分析及諧響應分析[J].金剛石與磨料磨具工程，2015，35(4)：41-45.