串聯倒擺的空氣彈簧隔振器中倒擺的穩定性分析

朱 煜, 喻 強, 徐登峰, 管高峰, 穆海華

(1. 電子科技大學 機械電子工程學院，成都 611731；2. 清華大學 機械工程系，北京 100084)

倒立的擺動裝置(倒擺)因其結構簡單、成本低廉等特點被廣泛應用于自動控制工程、機械工程等領域的各種設備中。Blitzer等[1-2]在1965年分別利用牛頓力學法和拉格朗日方程法建立了倒擺的運動方程，并分析了正弦激勵作用時倒擺的運動特性。Kalmus[3]在1970年分析了脈沖激勵作用時倒擺的運動特性。Pinoli等[4-5]分別在1993年和1994年開始提出倒擺可用于水平隔振裝置中。但倒擺作為一種負剛度隔振系統單獨使用時極不穩定，必須聯合其它裝置一起使用。Losurdo等[6-9]相繼提出倒擺可聯合金屬彈簧、鈹青銅片、高強度撓性關節、復合擺等一起使用，用于各種精密隔振系統中。

近年來，倒擺聯合空氣彈簧使用逐漸成為研究熱點[10-15]。空氣彈簧具有較低的垂直剛度和較大的水平剛度，倒擺具有較低的水平剛度和較大的垂直剛度，將倒擺與空氣彈簧串聯使用時，倒擺的水平剛度遠小于空氣彈簧的水平剛度而垂直剛度遠大于空氣彈簧的垂直剛度，串聯使用后的隔振器等效水平剛度近似為倒擺的水平剛度，等效垂直剛度近似為空氣彈簧的垂直剛度。因此，倒擺串聯空氣彈簧使用不僅解決了倒擺單獨使用時極不穩定的問題，還解決了空氣彈簧垂直和水平方向的隔振性能無法兼顧的問題，使隔振器垂直和水平方向同時實現了低剛度(低固有頻率)。

雖然串聯倒擺的空氣彈簧隔振器具有上述的諸多優點，但在使用過程中依然會出現倒擺穩定性問題。該穩定性問題主要是指倒擺偏離初始平衡位置后無法回復到原來的位置或回復時間過長。文獻[16-18]中提到單擺在偏離初始平衡位置一個較小的角度后會受到一個指向平衡位置，大小與位移成正比的回復力的作用，從而使單擺能夠回復到原來的位置。倒擺作為一個倒立的單擺，串聯空氣彈簧后在水平外力作用下，會產生水平位移和偏轉(活塞偏轉)，同時也會受到空氣彈簧給予的回復力和回復力矩(回復力產生的矩)作用。回復力和回復力矩的大小和方向決定著倒擺能否回復到原來的位置。所以，以回復力和回復力矩的大小和方向來衡量倒擺的穩定性。

為此，本文從串聯倒擺的空氣彈簧隔振器各個結構參數出發，分析其對倒擺穩定性的影響，利用牛頓力學法建立倒擺穩定性的力學模型，推導出回復力和回復力矩的數學模型，再結合具體實例對該數學模型進行仿真分析，尋找影響倒擺穩定性的主要結構參數，最后根據仿真分析結果指導空氣彈簧隔振器的結構優化設計。

1 理論分析

如圖1所示，串聯倒擺的空氣彈簧隔振器主要由負載、擺桿、上活塞、橡膠膜片、下活塞、壓環、腔室和空氣彈簧等組成。外力作用下，擺桿會移動到圖中豎直雙點劃線所示位置，上下活塞也會繞著下活塞與擺桿的接觸點偏轉至圖中雙點劃線矩形所示位置，橡膠膜片由圖中黑色粗實線變成雙點劃線所示位置。如點劃線圓所示，左側橡膠膜片與活塞的接觸面積變大，右側橡膠膜片與活塞的接觸面積變小，在空氣彈簧內部氣壓的作用下活塞(擺桿和負載)因受到回復力和回復力矩作用而回復到原來的初始平衡位置。

圖1 串聯倒擺的空氣彈簧隔振器示意圖Fig.1 The air spring vibration isolator in series with the inverted pendulum

如圖2所示，活塞的重心為O2，活塞與擺桿的接觸點為O1，F11和F12分別為活塞受到垂直于上活塞外表面的壓力，F21和F22分別為活塞受到沿著上活塞外表面向上的拉力，Fp為空氣彈簧內部氣體對活塞的有效支撐力，mg為活塞的重力，Mg為負載等對活塞的壓力。各力的合力就是活塞受到的回復力F，各力在O1點產生的合力矩就是活塞受到的回復力矩T。橡膠膜片與活塞接觸面積的變化以及空氣彈簧內部氣壓的存在是回復力和回復力矩產生的主要原因，先分析橡膠膜片與活塞接觸面積的變化和空氣彈簧內部氣體壓力的大小，再逐個分析圖2中各力的大小和方向以及在O1產生力矩的大小和方向，便可得到總的回復力F和回復力矩T。

圖2 活塞的受力分析Fig.2 The force analysis of the piston

1.1 橡膠膜片與活塞接觸面積的變化

將橡膠膜片與活塞的接觸面沿著活塞周向劃分成無數個小段，每個小段的高度即為該段對應的橡膠膜片與活塞接觸的長度。活塞發生如圖1所示的偏轉后，橡膠膜片與活塞最左側邊線的接觸長度最長，與活塞最右側邊線的接觸長度最短。橡膠膜片與活塞接觸面每個小段的高度近似認為是從最右側最短接觸長度線性增加到最左側最長接觸長度，則求解橡膠膜片與活塞接觸面積的變化就相當于求解橡膠膜片與活塞的最長接觸長度和最短接觸長度。

如圖3所示，活塞由實線DMNH偏轉至雙點劃線D1M1N1H1，O為MN的中點，O1為M1N1的中點。設負載(擺桿)的水平位移為x，上活塞半徑為R，擺桿有效擺長為h，活塞偏轉角度為θ。則D和D1之間的水平距離Δx1和豎直距離Δy1以及H和H1之間的水平距離Δx2和豎直距離Δy2分別為

Δx1=hsinθ+Rcosθ-R-x

(1)

(2)

Δx2=hsinθ-Rcosθ+R-x

(3)

(4)

圖3 活塞偏轉示意圖Fig.3 The deflection of the piston

如圖4(a)所示，左側橡膠膜片由ABCD變為A1B1C1D1，橡膠膜片與上活塞的接觸長度由CD變為C1D1，設圓弧BC的半徑為r(包含橡膠膜片厚度)，圓弧B1C1的半徑為R1。橡膠膜片中簾布的存在使其無法被拉伸或壓縮而改變長度，則為

(5)

式(5)中∑為定值，則可得到R1為

(6)

則橡膠膜片與活塞的最長接觸長度L為

(7)

如圖4(b)所示，右側橡膠膜片由EFGH變為E1F1G1H1，橡膠膜片與活塞的接觸長度由GH變為G1H1，設圓弧F1G1的半徑為R2。同理，可得R2為

(8)

圖4 橡膠膜片變形示意圖Fig.4 The deformation of the elastomer diaphragm

則橡膠膜片與活塞的最短接觸長度l為

(9)

1.2 空氣彈簧內部壓強的計算

圖5 橡膠膜片與負載受力示意圖Fig.5 The force of the elastomer diaphragm and the load

由橡膠膜片的受力分析可知

(10)

空氣彈簧內部氣體對負載的有效支撐力Fp為

Fp=π(P1-P0)(R+d)2

(11)

由負載的受力分析可知

(M+m)g=F2+Fp

(12)

則空氣彈簧內部氣體壓力P1為

(13)

1.3 F11和F12產生的回復力和回復力矩

圖6 橡膠膜片與上活塞接觸示意圖Fig.6 The contact between elastomer diaphragm and upper piston

偏轉后的橡膠膜片與上活塞軸測圖如圖6(a)所示，主視圖如圖6(b)所示，橡膠膜片與上活塞的最長接觸長度C1D1為L，最短接觸長度G1H1為l。將圓環狀的橡膠膜片展開成如圖6(c)所示的平面狀，橡膠膜片與上活塞的接觸長度近似從G1H1處的l不斷線性增加到C1D1處的L，H1D1之間的長度為πR。

如圖7(a)所示，取一小段橡膠膜片MN，其與H1的夾角為α，對應的圓心角為dα。如圖7(b)所示，橡膠膜片MN受到垂直于其外表面的力dF，將該力正交分解成平行于H1D1的分力dF1和垂直于H1D1的分力dF3。將圖7(c)半圓弧H1ND1展開成圖7(d)的線段H1ND1，則線段MN的長度為

(14)

則作用在橡膠膜片MN的外表面的力dF為

(15)

如圖7所示，所有dF3的合力為零，dF1大小為

dF1=cosαdF

(16)

圖7 小段橡膠膜片“MN”Fig.7 A small part of the elastomer diaphragm “MN”

如圖8所示，記左側橡膠膜片所受到的所有分力dF1的合力為F11，其對點O1產生的有效力矩為T11；右側橡膠膜片所受到的所有分力dF1的合力為F12，其對點O1產生的有效力矩為T12，則F11、F12、T11和T12大小分別為(方向如圖8所示)

(17)

(18)

(19)

則合力F1和合力矩T1大小為(方向如圖8所示)

(20)

(21)

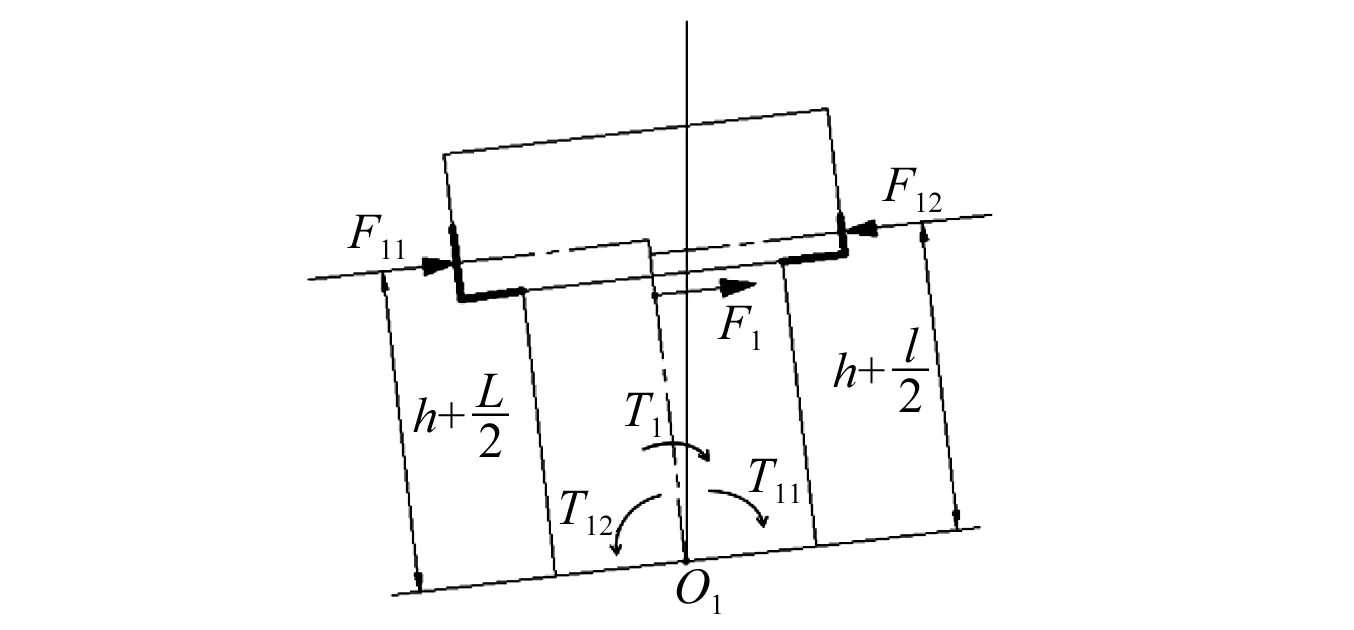
圖8 偏轉力矩T1示意圖Fig.8 The deflection torque T1

1.4 F21和F22產生的回復力和回復力矩

如圖9(a)所示，近似認為活塞偏轉后最左側橡膠膜片鼓起部分為直徑2R1的圓弧，最右側橡膠膜片鼓起部分為直徑2R2的圓弧。圖9(b)為橡膠膜片與活塞的軸測圖，圖9(c)為橡膠膜片與活塞的截面圖，取一小段橡膠膜片AB，其有效的投影面為CD，與水平軸線的夾角為β，對應的圓心角為dβ。橡膠膜片鼓起部分的有效投影面的長度近似認為是從2R1線性增加到2R2，則CD的長度為

(22)

則該段橡膠膜片對上活塞的拉力dF2為

(23)

圖9 小段橡膠膜片“AB”Fig.9 A small part of the elastomer diaphragm “AB”

如圖10(a)所示，記左側橡膠膜片對上活塞的所有拉力dF2的合力為F21，其對點O1產生的有效力矩為T21；右側橡膠膜片對上活塞的所有拉力dF2的合力為F22，其對點O1產生的有效力矩為T22，則F21、F22、T21和T22大小分別為(方向如圖10(a)所示)

(24)

(25)

(26)

則合力F2和合力矩T2大小為(方向如圖10所示)

(27)

T2=T21-T22=

(28)

1.5 活塞重力產生的回復力矩

設活塞的重心高度為h1，則重力mg對點O1產生的力矩T3大小為(方向如圖10(b)所示)

T3=mgh1sinθ

(29)

圖10 偏轉力矩T2、T3和T示意圖Fig.10 The deflection torque T2，T3 and T

1.6 總回復力和回復力矩

綜上所述，總回復力F和總回復力矩T的大小為(方向如圖10(b)所示)

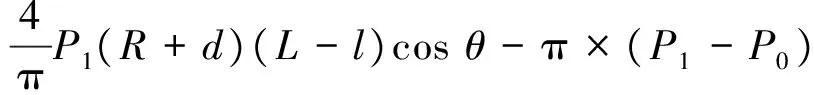
(30)

(31)

2 實例分析

某串聯倒擺的空氣彈簧隔振器實例如圖11所示，其各項參數值如表1所示。

圖11 空氣彈簧隔振器實例Fig.11 The actual air spring vibration isolator

參數名稱參數值負載的水平位移x/mm0～4擺桿的有效擺長h/mm519活塞的偏轉角θ/rad0～arctan(x/h)上活塞的半徑R/mm143橡膠膜片鼓起圓弧的半徑r/mm3橡膠膜片的厚度d/mm1橡膠膜片鼓起部分的總長度Σ/mm27．4活塞的總質量m/kg15．5活塞的重心高度h1/mm363．4負載的總質量M/kg3030標準大氣壓P0/Pa1．013×105重力加速度g/(m·s-2)9．8

將上述參數代入式(30)中，回復力F與水平位移x和偏轉角θ的關系如圖12(a)所示，回復力F均為負值，其絕對值表示回復力F的大小，負號表示回復力F的方向總是與負載水平位移x的方向相反。隨著水平位移x的增大，回復力F的大小不斷增大，隨著活塞偏轉角度θ的增大，回復力F的大小不斷減小。

將上述參數代入式(31)中，回復力矩T與水平位移x和偏轉角θ的關系如圖12(b)所示，回復力矩T絕對值表示回復力矩T的大小。隨著水平位移x的增大，回復力矩T的大小不斷增大，隨著活塞偏轉角度θ的增大，回復力矩T的大小先不斷減小后不斷增加。

圖12 回復力F和回復力矩T與水平位移x和偏轉角θ的關系Fig.12 The relationship between the restoring force F, the restoring torque T and the displacement x, the angle θ

3 仿真分析

倒擺穩定性主要取決于回復力F和回復力矩T的大小和方向，負載質量、活塞質量和重心高度等一定時，它們主要與擺桿擺長h、上活塞半徑R、橡膠膜片鼓起圓弧半徑r和橡膠膜片厚度d有關。下面分別分析這些參數變化對回復力F和回復力矩T大小和方向的影響。

3.1 擺桿擺長h對回復力F和回復力矩T的影響

如圖13所示，分別取不同的擺桿擺長h′，觀察回復力F和回復力矩T的變化。隨著擺桿擺長h的減小，回復力F的大小有所增加，加速活塞偏轉的力矩T大小有所降低。

圖13 擺桿擺長h的變化對回復力F和回復力矩T的影響Fig.13 The influence of the length h on the restoring force F and the restoring torque T

3.2 上活塞半徑R對回復力F和回復力矩T的影響

如圖14所示，分別取不同的上活塞半徑R′，觀察回復力F和回復力矩T的變化。隨著上活塞半徑R的減小，回復力F的大小有所增加，但加速活塞偏轉的力矩T大小也有所增加。

圖14 上活塞半徑R的變化對回復力F和回復力矩T的影響Fig.14 The influence of the radius R on the restoring force F and the restoring torque T

3.3 圓弧半徑r對回復力F和回復力矩T的影響

如圖15所示，分別取不同的橡膠膜片鼓起圓弧半徑r′，觀察回復力F和回復力矩T的變化。圓弧半徑r的變化對回復力F和回復力矩T的影響忽略不計。

圖15 圓弧半徑r的變化對回復力F和回復力矩T的影響Fig.15 The influence of the arc radius r on the restoring force F and the restoring torque T

3.4 橡膠膜片厚度d對回復力F和回復力矩T的影響

如圖16所示，分別取不同的橡膠膜片厚度d′，觀察回復力F和回復力矩T的變化。橡膠膜片厚度d的變化對回復力F和回復力矩T的影響忽略不計。

圖16 橡膠膜片厚度d的變化對回復力F和回復力矩T的影響Fig.16 The influence of the thickness d of the elastomer diaphragmon the restoring force F and the restoring torque T

4 結構優化設計

綜上所述，為了增加倒擺的穩定性，可以從以下方面進行結構優化設計：

(1)適當減小倒擺擺長h。串聯倒擺的空氣彈簧隔振器為了獲得更好的水平方向隔振性能只有采用較長的擺桿桿長h，這樣會降低倒擺的穩定性。因此，為了增加倒擺的穩定性，在隔振器的具體設計時必須適當減小擺桿擺長h。一方面可以增加回復力的大小，使負載、活塞和擺桿等的水平位移能更快地減小；另一方面也可以降低加速活塞偏轉的力矩大小，使每個水平位移對應的活塞偏轉角度有所降低。

(2)適當減小上活塞半徑R。在空氣彈簧內部氣體壓力有限的前提下，串聯倒擺的空氣彈簧隔振器為了追求更大的承載能力只有采用較大上活塞的半徑R，這樣也會降低倒擺的穩定性。因此，為了增加倒擺的穩定性，在隔振器的具體設計時必須犧牲承載能力而適當減小活塞半徑R。這樣可以增加回復力的大小，使負載、活塞和擺桿等的水平位移能更快地減小，雖然也會增加加速活塞偏轉的力矩大小，但增加了回復力的大小更為重要。

(3)降低負載的重心高度。負載一定的情況下，負載在活塞轉動支點處的轉動慣量與其重心高度的平方成正比，降低負載的重心高度可減小負載轉動慣量的大小，從而使負載、活塞和倒擺在初始平衡位置處更加穩定。

5 結 論

本文全面分析了空氣彈簧隔振器各個結構參數對倒擺穩定性的影響，得到了回復力和回復力矩的數學模型，通過對該模型進行實例和仿真分析發現回復力和回復力矩主要與倒擺擺長h和上活塞半徑R有關。一方面，可適當減小倒擺擺長和上活塞半徑來增加回復力的大小，增強倒擺的穩定性；另一方面，可適當降低負載的重心高度來降低負載在活塞轉動支點處的轉動慣量大小，使倒擺在平衡位置處更加穩定。

[ 1 ] BLITZER L. Inverted pendulum[J]. American Journal of Physics, 1965(33): 1076-1078.

[ 2 ] PHELPS F M Ш, HUNTER J H Jr. An analytical solution of the inverted pendulum[J]. American Journal of Physics, 1965(33): 285-295.

[ 3 ] KALMUS H P. The inverted pendulum[J]. American Journal of Physics, 1970(38): 874-878.

[ 4 ] PINOLI M, BLAIR D G, JU L. Tests on a low-frequency inverted pendulum system[J]. Measurement Science and Technology, 1993,4(9): 995-999.

[ 5 ] SAULSON P R, STEBBINS R T, DUMONT F D, et al. The inverted pendulum as a probe of anelasticity[J]. Review of Scientific Instruments, 1994, 65(1): 182-191.

[ 6 ] LOSURDO G, BERNARDINI M, BRACCINI S, et al. An inverted pendulum preisolator stage for the VIRGO susoension system[J]. Review of Scientific Instruments, 1999, 70(5): 2507-2515.

[ 7 ] YAGMUR L, GULMEZ T, HACIZADE F, et al. A new inverted pendulum to determine anelastic behavior of metals: design and characterization[J]. Review of Scientific Instruments, 2005, 76(9): 093903.

[ 8 ] TAKAMORI A, RAFFAI P, MARKA S, et al. Inverted pendulum as low-frequency pre-isolation for advanced gravitational wave detectors[J]. Nuclear Instruments and Methods in Physics Research A, 2007, 582(2): 683-692.

[ 9 ] 夏超，譚久彬. 基于復合擺倒擺串聯的光學儀器氣浮隔振方法研究[J]. 光電子激光，2011，22(10)： 1551-1556.

XIA Chao, TAN Jiubin. An air flotation vibration isolation method based on compond pendulum inverted pendulum-series for optical instruments[J]. Journal of Optoelectronics Laser, 2011, 22(10): 1551-1556.

[10] WATSON D C, PHILLIPS A H. Vibration isolator with low lateral stiffness: US6953109B2 [P]. United States Patent, 2005.

[11] BUTLER H, AUER F, VAN M, et al. Support device and lightographic apparatus : US7170582B2 [P]. United States Patent, 2007.

[12] 朱繼梅，俞寧長，鄒岳華. 倒擺式氣動隔振器：CN1487216A [P]. 2004.

[13] 譚久彬，夏朝，王雷,等. 基于球頭連桿的氣浮式正倒擺串聯機構的空氣彈簧隔振器：CN102072275 [P]. 2011.

[14] 楊潤，姜偉，朱襟成. 精密減振-定位復合系統建模與分析[J]. 機械與電子，2013(6)： 57-61.

YANG Run, JIANG Wei, ZHU Jincheng. Modeling and analysis of precision positioning and vibration isolation system[J]. Machinery & Electronics, 2013(6): 57-61.

[15] ARNDT E, OESTRICH W. Vibration isolator with pneumatic spring: US2016/0084339A1 [P]. United States Patent, 2016.

[16] 季文美，方同，陳松淇. 機械振動[M]. 北京：科學出版社，1985.

[17] 王亞民. 大學物理[M]. 西安：西北工業大學出版社，2011.

[18] 蒲華燕. 超精密隔振系統建模與控制方法研究[D]. 武漢：華中科技大學，2012.