2017年高考全國理綜Ⅱ卷第18題分析*

尹明德

(秦安縣第一中學 甘肅 天水 741600)

舉國矚目的2017年高考已經落幕，仔細琢磨理綜Ⅱ卷物理試題，考概念、考規律、考思想、考應用、考思維，重點考查“力與運動”的相關知識.其中，選擇題第18題，考生或許能蒙出答案，但在有限的時間內要真正弄通、弄透本題著實不易！為使學生能想通弄透此類問題，真正達到“分層次學習——知其然，深度學習——知其所以然”之效果，特此分析.

【原題】如圖1所示，虛線所示的圓形區域內存在一垂直于紙面的勻強磁場，P為磁場邊界上的一點.大量相同的帶電粒子以相同的速率經過P點，在紙面內沿不同方向射入磁場.若粒子射入速率為v1，這些粒子在磁場邊界的出射點分布在六分之一圓周上；若粒子射入速率為v2，相應的出射點分布在三分之一圓周上.不計重力及帶電粒子之間的相互作用.則v2∶v1為( )

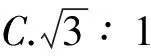
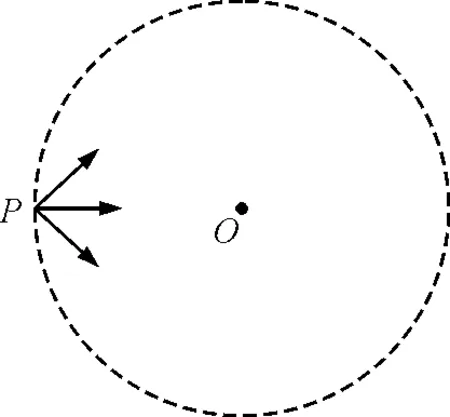
圖1 題圖

弄通問題：

(1)圓O的虛線邊界上從P點算起，“六分之一圓周”有6段、“三分之一圓周”有3段，哪些粒子射到分段點上(無數軌跡中找出特殊軌跡)？

(2)如何找出射到分段點粒子的軌跡圓心？

(3)怎樣找到粒子出射區段內相對應的P點入射區域？

弄透問題：

(1)利用數學知識，對磁場圓邊界進行“六分之一”或“三分之一”分割.

(2)只要找到一個射到分割點的粒子的軌跡圓心，利用幾何關系求出軌跡半徑(此時題目已經解出)，其余粒子的軌跡圓心均在以P點為圓心、以r1或r2為半徑的圓周上.

(3)“移動軌跡圓心——動態思維”，不難找出眾粒子的入射、出射范圍.

答后反思：如何通過構圖確定粒子的軌跡圓心？如何找出“臨界”軌跡？粒子運動有無對稱性？求粒子軌跡半徑的方法有幾種？

(1)

同理，當入射速率為v2時，無數軌跡的半徑均為

(2)

顯然

(3)

第一種情況：討論射入速率為v2，相應的出射點分布在三分之一圓周上的情況.

(2)過P點作PA⊥PO，則P→O表示指向圓心O進入磁場的一個粒子，它將從分段點B處背離圓心O沿O→B方向射出，由左手定則知P→A和B→A分別表示粒子在P和B兩點處所受洛倫茲力的方向，或作軌跡弦PB的垂直平分線，與PA相交于A，A點即為軌跡圓心，如圖2所示.

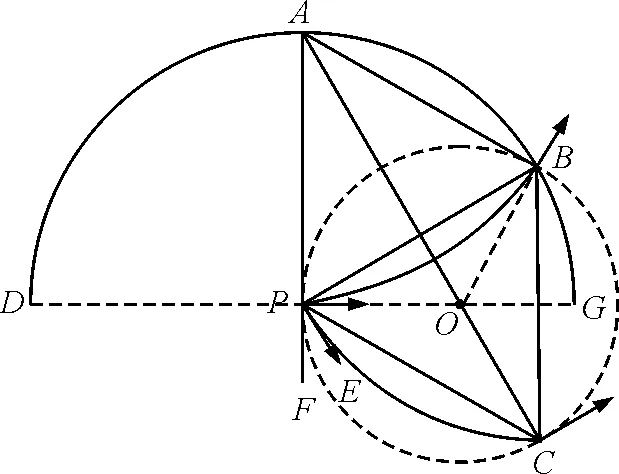
圖2 第一種情況分析圖

(3)因∠POB=120°，故∠POA=60°，以A點為圓心的粒子，其軌跡半徑為

(4)

式中R為圓區域半徑.

(4)因△PBA為等邊△，故BP=r2，故以B點為圓心，r2為半徑作過C點的圓弧，將是從P點沿P→E方向射入磁場的粒子的軌跡；因PE⊥PB，故

∠OPE=60° ∠EPF=30°

第二種情況：討論射入速率為v1，相應的出射點分布在六分之一圓周上的情況.

(2)過P點作Pa⊥Pc，則P→c進入磁場的一個粒子，它將從分段點b處沿垂直ba的方向射出，由左手定則知P→a和b→a分別表示粒子在P和b兩點處所受洛倫茲力的方向，或作軌跡弦Pb的垂直平分線Oa，與Pa相交于a，a點即為軌跡圓心，如圖3所示.

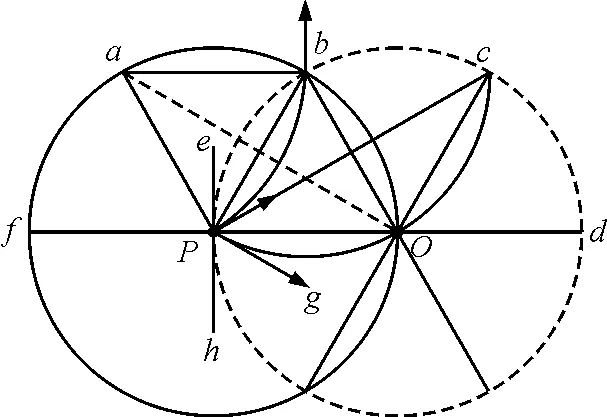
圖3 第二種情況分析圖

(3)因∠POb=60°，四邊形abOP為菱形，以a點為圓心的粒子，其軌跡過分段點b，半徑為

r1=R

(5)

(R為圓區域半徑)，至此，把式(4)、(5)代入式(3)得出本題選項是C.

(4)因△Pba為等邊△，故bP=r1，以b點為圓心，r1為半徑作過O和c點的圓弧，將是從P點沿P→g方向射出的粒子的軌跡；因Pg⊥Pb，故∠ePc=∠cPg=∠gPh=60°.

至此，讀者是否體會到本題才全面“貫通”了？這種探究性解題方法如同“剝蔥”之法，有的考生即使答案對了，思維上卻不一定如此清晰！

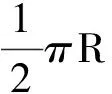
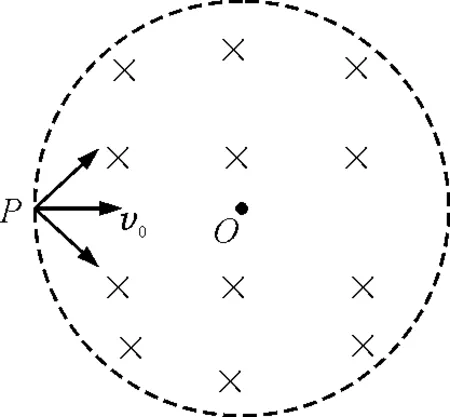
圖4 對比練習題圖

解析：(1)題設“……粒子均從由P點開始的弧長為……”，明確了從P點起的四分之一圓周和三分之一圓周射出區間.

(2)從離P點四分之一圓周的Q點或三分之一圓周的H點射出的粒子(見圖5和圖6)，其軌跡有何特點？

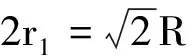
D選項正確.

(6)其他粒子的運動軌跡(劣弧或優弧)，入射點P至相應出射點的距離總比PQ和PH要小.

(7)前述高考題也能這樣求解出正確答案！真是歪打正著.

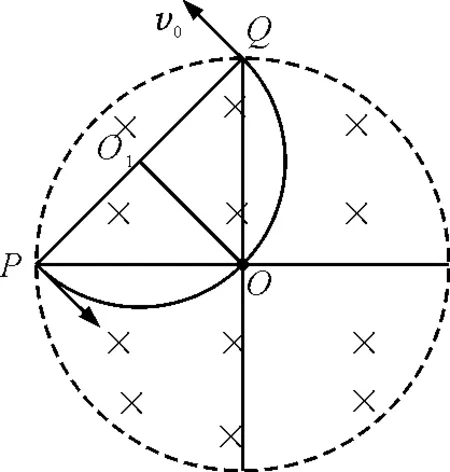
圖5 從Q點射出的軌跡圖

圖6 從H點射出的軌跡圖

對比兩題解析不難發現：因高考題關于粒子出射范圍敘述得模糊，使思維開放性增加；對選擇題師生著眼于迅速作答，常不書寫繁難的作答過程，這將制約著學生對問題深入、發散地思考，不利于“求異思維”的培養.

綜上可見，從大量粒子中提取1～2個“臨界”粒子，關鍵要抓住“分界點”，用構圖來尋找幾何關系；每個粒子的軌跡圓心是3條直線(圖2中)PA，OA，BA中任意兩條直線的交點；由幾何關系求半徑、由洛倫茲力等于向心力求半徑、運動軌跡關于軌跡弦的中垂線對稱是3個不變的思路；有的問題中，“臨界”軌跡是與一個或兩個邊界相切，有的問題中則是粒子通過二邊界的交點；此類問題均要具體分析、數理并舉、準確構圖、動態思維.