海量時空軌跡的梯形帶相似聚類
孫衛真,林秋慧,向 勇,趙秋香
1(首都師范大學 信息工程學院 計算機科學與技術系,北京 100048) 2(清華大學 計算機科學與技術系 網絡所,北京 100084) 3(山東省 濟寧市第一中學 高中數學組,山東 濟寧 272000)
1 引 言
由于GPS設備的逐漸普及,基于位置服務[1]的廣泛應用等,位置信息的獲取變得愈加便捷.毫無疑問,這些數據的匯集將是海量的、個體連續的.個體連續的位置信息數據按照采樣時刻連接而成后,可以得到該運動對象的時空軌跡.海量的時空軌跡背后隱藏的信息帶動了軌跡挖掘的發展,目前的應用范圍涵蓋了包括交通監管、人類行為、動物遷徙、自然風暴預測等等[2].因此,分析并聚類實時的海量時空軌跡數據,獲取典型的軌跡模式是非常有必要的.
然而,存儲開銷大、計算強度高、聚類幾何特征保留不完整等問題,是海量時空軌跡數據的聚類目前所面臨的主要挑戰[3,4].目前國內外在軌跡聚類方面的研究中,主要有以下幾個方向[6]:基于數據的稀疏度、基于空間劃分、基于興趣點以及基于軌跡的幾何特征等.其中,基于數據的稀疏度的方法,屬于數據挖掘的通用方法[7],但時間與空間復雜度都很高,不適用于海量時空軌跡的聚類;而基于空間劃分的方法,計算量相對較小,一般會結合LCSS方法并在明確的應用場景下使用[6,8];基于興趣點劃分的方法準確度較差,且在興趣點較多的地區,軌跡的校準與劃分將存在一定困難[9].而基于軌跡幾何特征方法的文獻則相對較少,其中,文獻[10]提出了一種基于結構相似度的軌跡聚類算法,與軌跡的幾何特征有一定的的相關性,但其對原始軌跡的要求較高.Lee等人[2]在2007年提出了一種新的基于幾何形狀的聚類擬合軌跡的方法,其方法解決了復雜軌跡之間的比較問題,但是對軌跡進行了近似描述,從而造成了軌跡的局部幾何特征丟失.
此外,實時海量的時空軌跡數據的聚類分析,還需考慮聚類的存儲與計算壓力的問題[11],目前已有的解決時效性問題的主要方法集中在對聚類前的軌跡數據進行簡化[12,13].現有的軌跡數據的簡化算法主要分為兩種[12]:一是局部軌跡數據簡化,二是整體軌跡數據簡化.局部軌跡數據的簡化主要針對待處理點,綜合分析并處理與鄰域點間的簡化關系,如距離閾值的過濾方法等[14].而整體的軌跡簡化大致包括如下四種經典的算法[3]:自頂向下(Top-Down,TD)[15]、自下而上、滑動窗口、開放窗口(Opening Window,OW).其中,OW算法的窗口大小是動態調整的,該算法適用于實時的流式軌跡數據.然而經典的OW算法在特殊軌跡的處理上并不理想,其一,其簡化后的軌跡保留的拐角信息點過少[12],導致減少了一些更準確的軌跡行進可能;其二,軌跡點過于密集時,其動態滑動窗口過長,從而明顯增加計算量.余超等在文章[16]中提出的角度可變的滑動窗口算法,能夠在轉角較大的情況下保留部分拐角軌跡點.而TD算法對于處理有規律且比較直的密集軌跡點時,效率非常高,可以彌補OW算法的不足.其經典方法有道格拉斯普克(Douglas-Peucher,DP)[4,13]算法,比較常見的有針對既定路線或網格的軌跡簡化[5,17].
以上的文獻分析可以看出,實時海量時空軌跡聚類的首要問題是由于幾何特征丟失導致的聚類不準確性[10].聚類的準確性取決于相似性度量方法,現有的軌跡間相似性度量方法主要集中在軌跡間距離上.如圖1所示,軌跡1、2與軌跡1、3的歐氏距離和是相同的,即相似度一致,然而軌跡1與軌跡2的幾何形狀特征明顯不一致,這無法達到相似性度量的準確性預期.此外,簡化應當能夠保留必要的軌跡數據特征,而現有的軌跡數據簡化方法不能直接應用到這一場景中.因此,有必要設計一種海量時空軌跡聚類的算法,用以保留必要的軌跡幾何特征,并兼顧時效性和準確性的問題.
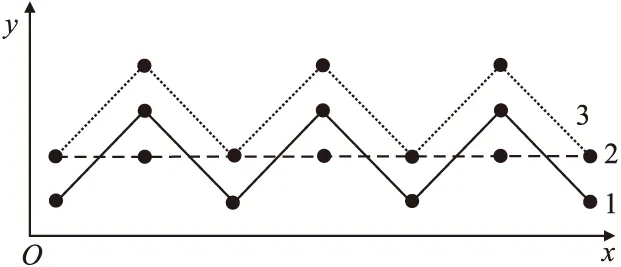
圖1 歐式距離相似度不準確性Fig.1 Inaccuracy of Euclidean distance similarity
針對海量時空軌跡的聚類,本文將貫徹時效性和準確性兩大原則進行闡述分析.首先,為減小計算量和存儲開銷,本文引入了一種綜合的軌跡簡化策略,不僅充分考慮了軌跡的時間和空間要素,更加入了軌跡的形狀特征因素.著眼于簡化后的時空軌跡數據的幾何特征,在前期的工作[18]中,我們結合計算幾何的方法對軌跡進行擴展,選擇了計算復雜度較低的軌跡梯形帶,定義了軌跡間的相似性度量方法.該方法可以在多項式時間內計算軌跡范圍,并判斷在不同時間跨度上的軌跡間相似性,在此基礎上,本文提出了海量時空軌跡的梯形帶相似聚類算法.該方法利用線性線段落在軌跡形成的梯形范圍內長度和本身長度的比值定義相似,在充分考慮軌跡幾何特征的條件下,能夠較為快速地獲取時空軌跡的有效聚類結果.最后,經海量真實時空軌跡數據測試集(北京市2010年04月06日出租車數據)測試,本文方法能快速并合理保留細節特征地進行軌跡數據簡化,準確有效地聚類同類軌跡并獲取合理的軌跡模式.
2 軌跡相似性度量
相似性度量作為軌跡聚類的標準,給出的定義越契合實際,軌跡聚類的效果也越好.此前的工作中,為減小計算量,采用梯形帶的方式簡化了時空軌跡帶[18].眾所周知,聚類后的軌跡簇一般是分區域的,那些區域可大可小,形狀不一.分在一個簇中的軌跡定義為相似的,相對于簇而言,這些軌跡是細小的.將軌跡簇類比于時空軌跡的梯形帶,那么相似于該梯形帶的軌跡也是細小的.因此,如圖2所示,假設存在一個軌跡梯形帶,令其他的軌跡均與軌跡帶的中心軌跡進行相似度匹配,即可得到有效的軌跡聚類,其直觀的度量標準為落在軌跡帶中軌跡長度與軌跡原長度的比值.
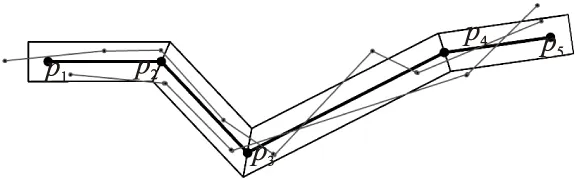
圖2 軌跡的梯形帶擴展及相似性示意Fig.2 Trapezoidal belt of trajectory and similarity diagram
經過以上論證,為更準確的描述軌跡間相似性,本文將在已有研究的基礎上,增加軌跡的幾何特征因素,提出如下的軌跡相似性度量模型.
2.1 時空軌跡的定義
運動對象的時空軌跡是由一系列采樣點,按照采樣時刻的順序連接而成的.傳統的軌跡描述方法[19]主要利用二維空間坐標,其缺點是,軌跡分類局限性較大,且無法非常準確地描述一條軌跡.為提高軌跡聚類的有效性,參考文獻[20]的做法,利用運動物體的特定編號、空間坐標、速度、方向等信息共同描述一條軌跡.
定義1.時空軌跡:一條時空軌跡可以表示為
Tr={(id,pi)|pi=(xi,yi,ti,vi,di),i=1,2,…,n}
(1)
其中,id表示軌跡Tr的特定編號,也即唯一標識,pi表示軌跡的第個采樣點,n表示軌跡的采樣點個數,(xi,yi)表示第i個采樣點的二維空間坐標,(ti,vi,di)分別表示軌跡Tr在第i個采樣點位置的時間信息、速度信息和方向信息.
定義2.原始軌跡:原始數據經過實時預處理后,按軌跡編號形成了一條條連續的軌跡.
(2)
定義3.軌跡模式:代表一組軌跡,初始聚類時,取原始軌跡中的一條經準確簡化而成.在類中軌跡達到一定量時,擬合這類軌跡并簡化,得到新的更合理的軌跡模式.

(3)
其中simiID為與該軌跡模式相似的原始軌跡的相似度similarity與oriID對的集合,初始為?.
2.2 時空軌跡梯形帶
定義4.時空軌跡梯形帶:表示如下
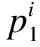
(4)
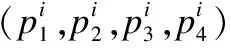
2.3 軌跡相交判斷
避免完全不可能相交的兩軌跡段進行軌跡相似計算,能夠有效減少計算量,通過判定構成軌跡段的基于坐標系的最小矩形是否相交,能夠粗略地判定軌跡段是否相交.
定義5.相交粗判:設有兩點(xn,yn)、(xn+!,yn+1),則兩點構成的基于坐標系的最小矩形為R,可以表示成R((xmin,ymin),(xmax,ymax)),其中(xmin,ymin)是R左下角點,(xmax,ymax)是的右上角點.
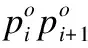
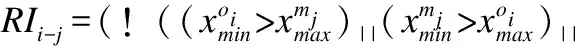
(5)
2.4 軌跡相交長度
1978年,Cyrus&Beck[21]提出了一種判斷直線與凸多邊形相交測試的算法—Cyrus&Beck裁剪算法(以下簡稱CB算法),其算法的復雜度為O(n).如圖3所示,除重合外,線段與多邊形相交主要有以下4種情況.
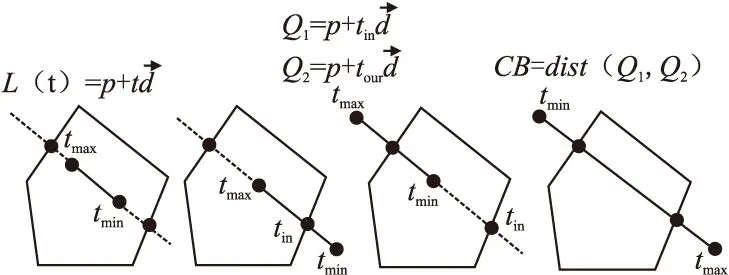
圖3 CB算法求解相交長度Fig.3 CB algorithm for intersection length
本文采用了增加重合情況的算法,用以計算軌跡段與梯形帶的相似長度.
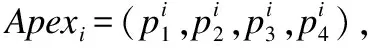
LenCB(Apexi,pjpj+1)
(6)
2.5 軌跡的相似性計算
為衡量時空軌跡的幾何相似性,在判定軌跡段與軌跡帶的相交情況后,利用軌跡段落在軌跡帶中的長度與軌跡段自身原長的比值,可以描述為軌跡的幾何相似性.
定義7.基于梯形帶的軌跡相似性:原始軌跡Tro與軌跡模式Trm產生的梯形帶Tp進行匹配,有軌跡段RIi-j=1.說明兩者可能相交,并可能產生軌跡段相似長度.則軌跡Tro與Trm的擴展梯形帶Tp的基于梯形帶的軌跡相似度(Trapezoidal Belt Based Similarity, TBST)可以表示為:
(7)
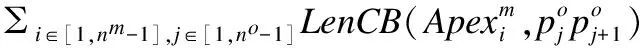
3 軌跡間的相似聚類算法
為實時處理海量真實的時空軌跡數據,通過對數據進行預處理,完成了清潔可用數據的獲取.為了保證實時海量時空軌跡聚類的時效性和準確性,針對軌跡數據存在大量密集點和直線軌跡點等特征,提出了海量時空軌跡的梯形帶相似聚類算法(Feature Preserved-Trapezoidal Belt,FP-TB),它包含2個階段.其一是綜合的特征保留簡化算法,它在保證能夠保留軌跡幾何特征的條件下,盡可能地進行數據存儲量的壓縮,并以不增加時間開銷為目的.其二是時空軌跡的梯形帶相似聚類算法,它在更優的時間內獲取更具價值的軌跡模式.下面將進行更為具體的描述.
3.1 必要的軌跡簡化策略
基于海量實時時空軌跡的時效性和準確性的需求,本文在前述內容的基礎上,為較快壓縮數據量、保留細節特征時盡量減少銳角并快速處理較長的密集軌跡點,在軌跡數據簡化方面,制定整體軌跡數據簡化為主,局部軌跡數據簡化為輔的綜合軌跡壓縮算法,以達到快速并合理保留軌跡特征地進行軌跡數據壓縮.
其中,局部鄰域點簡化(Neighborhood Points Compression,NPC)的核心思想在于,綜合分析待處理點與鄰域點,較快壓縮數據量.而整體軌跡數據簡化的算法又包含有兩種,一種是帶銳角限制的開窗算法(Angle Limited Opening Window,ALOW),用于整體的動態簡化并保留一些較為特殊的軌跡局部特征;另一種是針對擁有大量較為筆直的軌跡點,利用DP算法直接進行軌跡簡化.實時動態簡化以NPC算法為第一道關卡,ALOW算法為主要的簡化方法,在點閾值達到一定程度時再觸發DP算法,三者相輔相成.以下是詳細的算法描述.
算法1.綜合的特征保留簡化算法(Feature Preserved Simplification,FP).
輸入:原始軌跡Tro,局部簡化閾值SUBSIMPTHR,整體簡化閾值SIMPTHR,長直軌跡點閾值PTTHR
輸出:簡化后的軌跡Trosimp
算法步驟:
1)initialize(SUBSIMPTHR,SIMPTHR,PTTHR);//初始簡化閾值
2)copyInfo(Tro,Trosimp)//復制軌跡基本信息到簡化軌跡中
3)addp1toTrosimp//將軌跡起始點放入簡化軌跡中
4)for(next= 1;next≤n;next++){
5)for(i= 1;i≤n-next;i++){ //NPC算法
6)if(Dist(pnext,pnext+i)>SUBSIMPTHR){
7) delete {pnext+1,pnext+i-1} fromTro;
8)break;
9) }
10) }
11) countDP = 0;//用于觸發DP算法的flag
12)for(j= 1;j≤n-next-i;j++){//ALOW算法
13) LPDist=
Dist(Line(pnext,pnext+i+j),pnext+i+K),K∈[0,j);
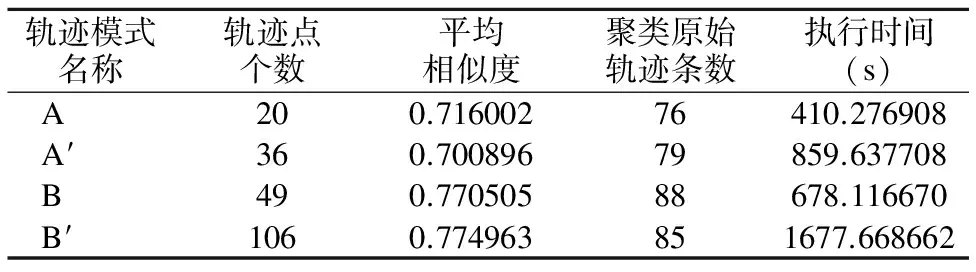
14)if(LPDist 15) countDP++; 16)else{ 17) Kmax=MAX(LPDist);//當有距離超過SIMPTHR時,選擇距離最大的浮動點 18)Qobt=FIRSTAngle(∠pbeforepnextpnext+i+Q>90°) ‖MAXAngle(∠pbeforepnextpnext+i+Q>90°), Q∈[Kmax,0] //注意向前浮動 19) addpnext+i+QobttoTrosimp;//浮動點放入簡化軌跡 20)next=next+i+Qobt,countDP=0; 21) } 22)if(countDP ≥PTTHR){ 23) //超過軌跡點閾值PTTHR,觸發DP算法. 24) addpnext+i+jtoTrosimp; 25) dpLine(pnext,pnext+i+j); 26) countDP=0,next=next+i+j; 27) } 28) } 29)} 30)returnTrosimp; 算法1是一個特征保留的軌跡簡化算法,它首先選擇從待簡化的原始軌跡Tro中,取第一個點作為簡化軌跡Trosimp的起始點,其后續進入的每一個點,均先與前一個簡化后的點進行NPC算法,再按照如下的ALOW算法簡化軌跡段. 前一條簡化后的軌跡段末端點作為起始點,從該點開始處理后面連續的n(n>=3)個點,第n個點設為浮動點:過起始點和浮動點做一條直線,分別計算中間n-2個點到直線的距離LPDist,若所有距離均小于距離閾值,則下一個數據點設為浮動點,計數;否則,選取與直線距離最大的點作為浮動點,進行“浮動點前移”:從該浮動點向前到起始點的下一點,依次作為浮動點計算三個點之間的夾角,利用函數FIRSTAngle選取浮動點,該浮動點是第一個和起始點間的軌跡段與前一條軌跡段成鈍角的點,將該浮動點加入到簡化軌跡Trosimp中,并成為下一個起始點;若所有兩軌跡段間的夾角都不大于90°,則利用函數MAXAngle選取與前一條軌跡段成最大角的浮動點加入到簡化軌跡Trosimp中,作為下一次循環的起始點. 當在ALOW算法簡化過程中的計數超過閾值時,觸發DP算法函數dpLine,將所有當前未處理的點取出,并將首尾兩點存入簡化軌跡Trosimp中,連接這兩點,計算中間所有點到該線的距離,若超過閾值,則將距離最大的點存入Trosimp中;連接首尾兩點,得到兩條直線,重復前述步驟,直到所有點到直線的距離均不超過閾值為止. 該算法得到的簡化軌跡,通過NPC算法減小了OW算法的繁復計算壓力,利用DP算法的優勢緩解了OW算法在處理長直軌跡點時的計算壓力,銳角特性的加入,則使得最終得到的簡化軌跡保留了一定的細節特征,能有效地應用于實際場景中,同時為后續的聚類分析減小了較大的工作量. 本文的相似性度量標準,基于軌跡的幾何特征,在擴展簡化后的軌跡模式Trm為梯形帶后,采用原始軌跡Tro落在軌跡模式Trm中的軌跡相似長度和,與原始軌跡Tro的長度比值來進行定義.這種方法,彌補了歐氏距離對軌跡幾何特征的忽略,解決了采用多邊形重合面積比定義相似性的不穩定問題.基于此,軌跡便能夠得到較好的聚類,并能夠得到更能代表聚類軌跡特征的軌跡模式.具體算法如下: 算法2.海量時空軌跡的梯形帶相似聚類算法(Trapezoidal Belt Based Clustering,TB). 輸入:原始軌跡集合I={Troi,i=1,2,…,k},其中原始軌跡為實時增加的;軌跡模式集合Q={Trmi,i=1,2,…,s},初始為空集?,隨聚類的進行而增長;相關參數:軌跡帶寬度WIDTH,相似度閾值SIMILARTHR 輸出:軌跡模式類集合Q 算法步驟: 1)initialize(WIDTH,SIMILARTHR);//初始梯形帶寬度、相似度閾值 2)Q=?;//初始化軌跡模式類集合Q為空集 3)for(eachTrokin theI){ //遍歷集合的原始軌跡 4)if(Q==?){ 5) createNewTrm(Tro,Trm);//生成第一條軌跡模式Trm 6) addTrmtoQ;//將Trm加入到軌跡模式類集合Q中 7) } 8)else{ 9) similarflag=false; 10)for(eachTrmsin theQ){ //遍歷集合Q的軌跡模式 11) creatApex(Trms,WIDTH);//依據軌跡帶寬度生成軌跡模式梯形帶 13)if(TBBS>SIMILARTHR){ 14) add(TBBS,ido)tosimiID;//維護當前Trm的simiID 15) similarflag=true; 16) } 17) } 18)if(similarflag ==false){ 19) createNewTrm(Tro,Trm); 20) addTrmtoQ;//將Trm加入到軌跡模式類集合Q中 21) } 22) } 23)} 算法2在初始時,初始化軌跡模式集合Q為空集,相關參數的梯形帶寬度WIDTH和相似度閾值SIMILARTHR.對所有在原始軌跡集合I中的所有原始軌跡,與所有在軌跡模式集合Q中的每一條軌跡模式進行相似度計算.首先生成簡化后的軌跡模式梯形帶,采用前述的相似性度量模型,計算兩軌跡間的相似度TBBS的值.繼而判斷當相似度的值大于相似度閾值SIMILARTHR時,認為該原始軌跡Tro與當前Trm相似,維護當前Trm的simiID集合,從而達到聚類效果.最后,若當前軌跡模式集合Q中沒有任何一條軌跡模式Trm與該原始軌跡Tro相似的話,依據該原始軌跡Tro生成一條軌跡模式Trm并參與后續計算. 從此處可以看出,軌跡模式所含數據點越多,則軌跡模式段越多,軌跡模式所對應的梯形帶中所含梯形越多,這樣,計算原始軌跡在梯形帶內的長度時,計算量就會越大,所以,軌跡模式是簡化后的軌跡,而且,簡化后的軌跡做軌跡模式與原始軌跡計算的相似度和未簡化前的軌跡做軌跡模式與原始軌跡計算相似度,兩者相似度相差不大,而前者的計算量則較后者大大減小了. 在給出具體算法的基礎上,分析算法的時間復雜度是很有必要的.通過時間復雜度的分析,能夠進一步的改進和優化算法的結構,以達到更加實時高效的目的. 算法1是一個綜合特征保留的軌跡簡化算法,為了追求最好的效率,可能需要反復執行,反復對軌跡點進行簡化,進而減少軌跡點的數量,對m條軌跡,其執行次數為O(m).對每個被保留的軌跡點而言,需要在其他剩余的軌跡點中,尋找下一個被保留點,候選的軌跡點共有O(n)個.因此,每次執行的算法時間復雜度最差為O(n2),最好的情況為O(log2n),其中n表示軌跡集合中軌跡的數量. 算法2是海量時空軌跡的梯形帶相似聚類算法,針對算法1產生的軌跡集合形成的原始軌跡,其軌跡的平均長度為O(n-1),對于每個軌跡點,需要在m條軌跡模式中進行相似度擬合,因此,算法2的時間復雜度為O(n-1)O(m). 其中,算法2由于原始軌跡的個數是實時增加的,其執行的效率主要取決于在聚類過程中形成的軌跡模式條數,當軌跡模式較少,其執行效率較高,反之,執行效率降低.目前本算法對待軌跡模式的增加主要取決于軌跡間相似度的閾值,后續將會基于此進行有效的改進. 以上分析可知,本文提出的FP-TB算法,在計算軌跡相似性時,增加了特征保留的軌跡點簡化,減少了大量的軌跡點,其對較為筆直和密集軌跡點的簡化大大提高了軌跡的簡化執行效率,利用這些簡化后的軌跡點進行相似度計算,充分減少了計算量.增加的軌跡幾何形狀的因素,則使得本算法所得的軌跡聚類結果更加準確. 在實驗部分,采用真實數據擴展的數據集對算法的可用性進行分析.其中真實數據集為2010年04月06日的30382520條北京市出租車數據,通過過濾得到較為清潔的數據,并在此基礎上利用空車與重車標志位分割軌跡,共得到可用軌跡35380條.使用該數據集的優勢在于,它包含大量的軌跡信息,包括軌跡的速度、角度、時間、位置信息、軌跡標識、類別信息等,并且這些軌跡信息都是真實的,其軌跡出現的情況均為真實應用環境的情形,能夠驗證本文所述方法的真實有效性. 實驗的硬件環境為:服務器端Ubuntu 14.04,內存2.00GB,數據庫端為Windows 7系統,安裝Oracle DB 11g,算法實現代碼為C++,并均在服務器終端進行測試運行. 4.1.1 軌跡簡化算法的幾何特征保留情況 本文提出的特征保留的軌跡簡化算法FP,其主要目標是在不影響軌跡簡化速率的基礎下,盡可能多的保留原始軌跡的有效特征.以較小的空間開銷,保留更多的軌跡特征,其軌跡的可用性越高,反之亦然.在該算法中,有三個閾值需要確定,其中僅有SIMPTHR閾值是與簡化效果密切相關的距離閾值. 由于其距離閾值所針對的點均為地圖上的點,而就中國的情況而言,緯度范圍從3°51′N至53°33′N,跨度較大,因此不適合在任意緯度指定固定的閾值.為了獲取更為合理的閾值,在指定閾值時,以千米km為單位,指定閾值為αkm,則不同緯度的緯度閾值由以下公式(8)換算得到: (8) 下面的實驗結果展現了在不同α值決定的SIMPTHR閾值下,本文算法FP與OW算法所得的簡化軌跡的對比結果. 圖4-圖6中虛線均代表原始軌跡,共17個點,左圖的實線為OW算法簡化后的軌跡,右圖實線則是本文算法FP簡化后的軌跡.如圖5所示,在本文的算法中,在保留了原始軌跡中的第8個點之后,若利用OW算法則下一個點為第10個點(即左圖算法中保留的第6個點),由于第8個點和前一個被保留點所成的線段與第8、10個點所成的線段夾角為銳角,本文的算法利用“浮動點前移”,到第9個點(即右圖中保留的第7個點),使得兩者之間的夾角不是銳角.利用OW算法簡化后的軌跡均含有1個銳角,而本文算法FP簡化后的軌跡則不含銳角,且簡化結果較為穩定. 圖4 值為0.01km時OW與FP的簡化效果Fig.4 Simplified results of OW and FP at α=0.01km 圖5 值為0.02km時OW與FP的簡化效果Fig.5 Simplified results of OW and FP at α=0.02km 圖6 值為0.03km時OW與FP的簡化效果Fig.6 Simplified results of OW and FP at α=0.03km 縱向比較圖4、圖5、圖6可知,隨著α值為0.01km、0.02km、0.03km,OW算法僅在值較小時才能保留原始軌跡的幾何特征,而本文的算法FP,則能夠在較大范圍內均保持簡化后的原始軌跡不失真.因此,本文算法FP較OW算法在實際應用中更為廣泛. 4.1.2 執行時間比較 本文所使用的真實的出租車數據集中,存在個體連續的大量密集點、較長時間的直線行駛和部分大型立交橋的轉彎行駛軌跡點,因此該簡化算法主要基于以上的數據特征進行.描述的是,在使用α=0.02km時,OW、ALOW以及本文所述的FP簡化算法,在壓縮率及執行時間方面的表現.其中,簡化的總點數W為3651685個點,形成了35380條原始軌跡. 結合上述實驗一及表1數據可以得到,本文的綜合特征保留算法FP的簡化較OW算法能夠保留更多原始軌跡的特征點,約多了6.75%.由于壓縮率數值越大,壓縮后的軌跡點所需的存儲空間也越大,而本文算法FP較OW算法的整體壓縮率增加了2.01%,存儲空間開銷隨之增大,但這一比例屬于存儲的可接受范圍.而對比ALOW算法,本文算法FP保留的軌跡點總數約少了2.36%,整體壓縮率減少了0.77%.這一差異性是由于NPC及DP算法的簡化造成的,而在執行時間減少諸多的情況下,這一情況基本可以忽略. 表1 各簡化算法的壓縮率及執行時間Table 1 Compression rate and execution time of each algorithm 通過觀察表1可以發現,同等實驗條件下,純粹的ALOW算法由于其時間復雜性較OW算法高,其運行時間較OW算法高出約13%.對于海量的軌跡數據而言,時間上的開銷是較難容忍的,因此需要對ALOW算法做進一步的改進.同樣地,從上表也可以看出,本文的FP算法較OW算法的運行時間縮短了約25.82%,較純粹的ALOW算法的執行時間縮短了約34.17%.這主要是因為NPC和DP算法有效地簡化和壓縮了這些增長的密集點和長直點,減小了ALOW以及OW算法的窗口,迭代次數隨之減少,執行的時間自然減少.以上數據結果說明,增加了NPC算法和DP算法來進行執行效率上的改進結果是卓有成效的,達到了縮短執行時間的目的.因此本文提供的FP算法是有效的,且更為高效的. 4.2.1 梯形帶寬度width對軌跡間相似的影響 本文提出的海量時空軌跡的梯形帶相似聚類算法FP-TB中,閾值width是影響軌跡間相似判斷的主要因素.下面是實驗獲取的某一類軌跡模式聚類的實驗結果,展現了在不同的width取值下,本文算法FP-TB在同一類軌跡中,其平均相似度的變化. 圖7 不同width下同類軌跡的平均相似度Fig.7 Average similarity of similar trajectories under different width 其中灰色底帶表示軌跡模式,黑色線條表示與之相似的原始軌跡,閾值width是影響梯形帶的半帶寬. 圖7(a)顯示的是width=0.04km時,直線型軌跡的其中一類所有相似軌跡與軌跡模式的相似度平均值,其相似度平均值顯示為0.765518.圖7(b)顯示的是width=0.05km時,直線型軌跡的其中一類所有相似軌跡與軌跡模式的相似度平均值,其相似度平均值顯示為0.818084. 根據以上的實驗結果,橫向比較圖7(a)與圖7(b)不難得出,隨著梯形半帶寬width值的增大,其聚類的軌跡相似度平均值也隨之增大,這說明類中的原始軌跡與軌跡模式的相似度也是增大的.這是符合前文所述相似性度量的結果,因此本文提供的FP-TB算法的相似性度量模型是行之有效的,且能準確有效的進行各類軌跡的聚類. 4.2.2 軌跡聚類結果及執行時間的比較分析 本文所用的真實出租車數據集,具有幾何走勢明顯的特征,對于這類軌跡,其主要目標是盡可能保證軌跡聚類的準確性,并挖掘出有價值的軌跡模式信息.本文從35380條原始軌跡中進行挖掘,其獲取的軌跡模式較多,下面將舉例給出直線型軌跡模式和環型軌跡模式的聚類結果,以驗證聚類的有效性,其梯形帶寬度width=0.05km,軌跡的相似度閾值SIMILARTHR=0.65. 圖8 不同類型的軌跡聚類結果Fig.8 Clustering results of different types of trajectories 圖8顯示的是根據本文所給的相似性度量模型,對原始軌跡集合進行聚類后所得的不同類型的軌跡模式.圖8(a)顯示的是簡單的直線型軌跡模式,其基本呈直線走勢,表明了所有與該直線型軌跡模式相似的原始軌跡的平均相似度為0.716002.參照北京市地圖可以發現,該軌跡模式表示去往首都機場的機場線路徑,說明在一天內,出租車去往首都機場的出行頻次是較高的.圖8(b)顯示的則是環型軌跡模式,其走勢為閉合的環線,圖中表明所有與該環型軌跡模式相似的原始軌跡的平均相似度為0.770505.該軌跡模式表示由西便門橋、右安門橋、左安門橋、東便門橋所形成的環線,并去往雙井橋附近.該區域有較多辦公大樓,屬于出租車司機的長期巡客區域,而雙井附近有較多居民區,因此這一路線也是出租車經常會走的路線.這些軌跡模式均符合北京市的實際交通路況,說明本文的相似性度量模型對于各類軌跡模式均是有效的,而環型軌跡中保留的部分拐角信息,則是出于幾何特征保留的考慮,由此可見,該聚類結果具備準確性. 此外,為定量比較聚類結果的執行時間,做了如下的幾組實驗來驗證.其中軌跡模式A、B分別是軌跡模式A′、B′簡化后的軌跡,與之聚類的原始軌跡為簡化后的35380條出租車軌跡. 通過3.3的算法分析可知,本文所述的FP-TB算法其執行效率主要取決于軌跡模式的條數和單條軌跡模式的段數,其中軌跡模式條數主要由原始軌跡數據集決定.由表2可以看出,相同的軌跡在簡化前后聚類所得的原始軌跡集合相差不大,其平均相似度的差別亦不大.而簡化后的軌跡聚類時間大約都減少了50%,其中軌跡模式A較軌跡模式A′的聚類執行時間減少了52.2732%,軌跡模式B較軌跡模式B′的聚類執行時間減少了59.5798%. 表2 FP-TB算法與僅TB的聚類方法的執行時間比較Table 2 Comparison of the execution time between FP-TB and TB clustering method 綜合在真實數據集上的實驗測試可以發現,本文提出的FP-TB算法可用性較高,并在考慮到軌跡幾何特征后,能夠在不影響執行時間的情況下保留重要的原始軌跡特征.在此基礎上,通過提出的相似性度量模型,計算原始軌跡落在軌跡模式梯形帶內的長度總和與原始軌跡線段的長度和之比定義相似性,對原始軌跡進行準確聚類,這一聚類方法能夠有效地對包括直線型與環型交叉等各類軌跡進行聚類,且執行時間較不經過處理直接進行聚類的方法快了近50%.因此,本文提出的FP-TB聚類算法是行之有效的. 本文在分析了海量時空軌跡數據的空間和時間特性后,考慮到已有的聚類算法在計算軌跡相似性時忽略了軌跡的幾何特征對聚類結果的影響,導致獲取的軌跡模式的部分重要細節特征失真的問題,針對出租車數據特征進行的軌跡挖掘,提出了FP-TB算法.第一階段的FP算法從存儲效率和保留簡化后的細節特征出發,制定了整體簡化為主,局部簡化為輔的軌跡簡化方案.第二階段的TB算法,增加軌跡幾何特征的影響因素,提出了一種新的相似性度量模型.并以此為主要依據并通過一定的相似度閾值準確篩選和挖掘相似的時空軌跡簇,進行海量時空軌跡的聚類分析.通過真實軌跡數據集上的實驗可以看出,本文算法在保留更多的軌跡原始特征的情況下,能夠準確有效地聚類同類軌跡以獲取典型的出租車行駛軌跡;而對不同類的軌跡,其執行效率均有不同程度的提升,因此具有更高的實際意義. 在未來的研究工作中,我們將考慮在聚類過程中軌跡模式的局部增刪與軌跡模式本身的動態調整,以獲取更切合實際的軌跡模式,減小計算開銷. [1] Gruteser M,Grunwald D.Anonymous usage of location-based services through spatial and temporal cloaking[C].Proceedings of the 1st International Conference on Mobile Systems,Applications and Services,ACM,2003:31-42. [2] Lee J G,Han J,Whang K Y.Trajectory clustering:a partition-and-group framework[C].ACM SIGMOD International Conference on Management of Data,ACM,2007:593-604. [3] Keogh E,Chu S,Hart D,et al.An online algorithm for segmenting time series[C].Data Mining,ICDM 2001,Proceedings IEEE International Conference on.IEEE,2001:289-296. [4] Meratnia N,Rolf A.Spatiotemporal compression techniques for moving point objects[C].International Conference on Extending Database Technology,Springer Berlin Heidelberg,2004:765-782. [5] Muckell J,Hwang J H,Lawson C T,et al.Algorithms for compressing GPS trajectory data:an empirical evaluation[C].Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems,ACM,2010:402-405. [6] Su H,Zheng K,Wang H,et al.Calibrating trajectory data for similarity-based analysis[C].Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data,ACM,2013:833-844. [7] Simoudis E,Livezey B K,Kerber R G.Method for generating predictive models in a computer system:U.S.Patent 5,692,107[P].1997-11-25. [8] Su H,Zheng K,Huang J,et al.Calibrating trajectory data for spatio-temporal similarity analysis[J].The VLDB Journal,2015,24(1):93-116. [9] Fu Z,Hu W,Tan T.Similarity based vehicle trajectory clustering and anomaly detection[C].Image Processing,2005.ICIP,IEEE International Conference on.IEEE,2005,2:II-602. [10] Yuan Guan,Xia Shi-xiong,Zhang Lei,et al.Trajectory clustering algorithm based on structural similarity[J].Journal on Communications,2011,32(9):103-110. [11] Thuraisingham B,Khan L,Clifton C,et al.Dependable real-time data mining[C].Eighth IEEE International Symposium on Object-Oriented Real-Time Distributed Computing,IEEE Computer Society,2005:158-165. [12] Chen Y,Jiang K,Zheng Y,et al.Trajectory simplification method for location-based social networking services[C].Proceedings of the 2009 International Workshop on Location Based Social Networks,ACM,2009:33-40. [13] Douglas D H,Peucker T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].Cartographica:The International Journal for Geographic Information and Geovisualization,1973,10(2):112-122. [14] Tobler W R.Numerical map generalization,and notes on the analysis of geographical distributions[M].Department of Geography,University of Michigan,1966. [15] Hershberger J E,Snoeyink J.Speeding up the douglas-peucker line-simplification algorithm[M].University of British Columbia,Department of Computer Science,1992. [16] Yu Chao,Guo Qing,Xie Wen-jun,et al.A method of fast geomagnetic matching based on orientation alterable sliding window[J].Computer Simulation,2015,32(3):86-89. [17] Yu J,Chen G,Zhang X,et al.An improved Douglas-peucker algorithm aimed at simplifying natural shoreline into direction-line[C].Geoinformatics(GEOINFORMATICS),2013 21st International Conference on.IEEE,2013:1-5. [18] Zhao Qiu-xiang.Trajectory clustering algorithm based on trapezoid belt similarity measure[D].Beijing:Graduate School of Beijing Normal University,2015. [19] Hwang J R,Kang H Y,Li K J.Spatio-temporal similarity analysis between trajectories on road networks[C].International Conference on Conceptual Modeling,Springer Berlin Heidelberg,2005:280-289. [20] Hu Hong-yu.Research on methods for traffic event recognition based on video processing[D].Changchun:Jilin University,2010. [21] Cyrus M,Beck J.Generalized two-and three-dimensional clipping[J].Computers & Graphics,1978,3(1):23-28. 附中文參考文獻: [10] 袁 冠,夏士雄,張 磊,等.基于結構相似度的軌跡聚類算法[J].通信學報,2011,32(9):103-110. [16] 余 超,郭 慶,謝文俊,等.地磁導航基于方向可變滑動窗口快速匹配方法[J].計算機仿真,2015,32(3):86-89. [18] 趙秋香.基于梯形帶相似性度量的軌跡聚類算法[D].北京:北京師范大學,2015. [20] 胡宏宇.基于視頻處理的交通事件識別方法研究[D].長春:吉林大學,2010.3.2 海量時空軌跡的梯形帶相似聚類
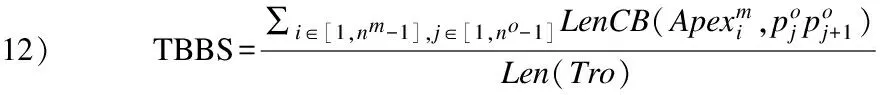
3.3 算法時間復雜性分析
4 測試與性能分析
4.1 軌跡簡化的實驗結果
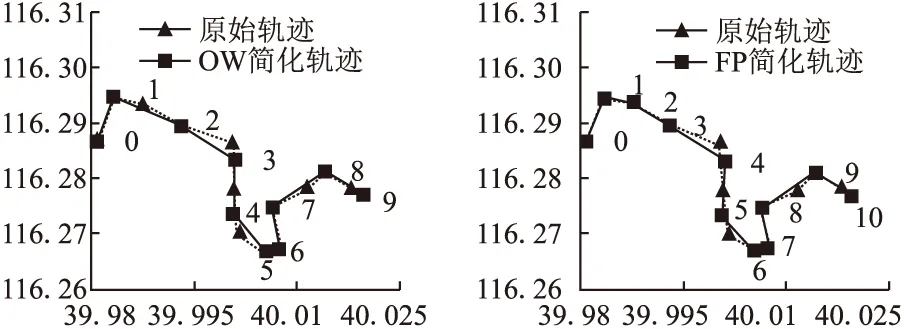
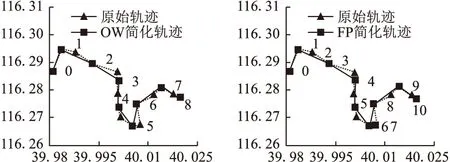
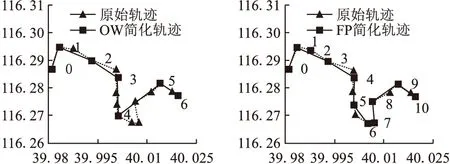
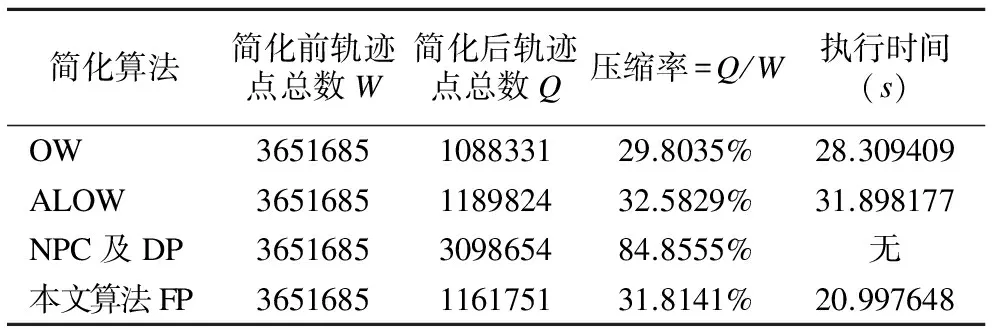
4.2 軌跡聚類的實驗結果

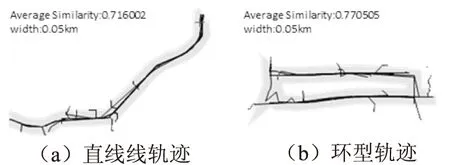
5 結束語

