時間權重遞增的協同過濾算法

史長瓊,夏廣偉,劉井平,何湘妮

1(長沙理工大學 智能交通大數據處理湖南省重點實驗室,長沙 410114) 2(長沙理工大學 計算機與通信工程學院,長沙 410114)

1 引 言

隨著信息技術的發展,推薦技術逐漸成為各領域重要的研究內容.目前,基于協同過濾的推薦系統不僅廣泛應用于電商網站,包括 Amazon、Netflix、Taobao,而且也應用于其他領域,如:電視節目推薦、網頁個性化推薦等.

協同過濾技術主要可分為兩大類:基于內存的協同過濾和基于模型的協同過濾[1].其中,基于內存的協同過濾又分為基于用戶的和基于項目的.基于用戶的協同過濾是通過尋找目標用戶的鄰近用戶,根據鄰近用戶對項目的評分,向目標用戶推薦預測評分為Top-N的項目;基于項目的協同過濾根據用戶對相似項目的評分,預測用戶對目標項目的評分,當需要預測某個目標項目的評分時,可以通過用戶對目標項目的若干近鄰項目進行估計來實現.

基于項目的協同過濾推薦算法(Item-based Collaborative Filtering,ItemCF)無論在研究中還是在實際應用中都有著重大的突破.然而傳統的協同過濾算法并沒有考慮用戶的興趣隨時間的推移而發生變化,認為評分數據在不同時期對于當前的影響是等同的,導致推薦的信息可能是過時的或者不是用戶當前感興趣的信息,影響了算法的準確性.針對傳統協同過濾算法存在推薦信息低時效性這個問題,文獻[9-15]在對數據的處理過程中考慮到了時間權重的變化,認為評分信息所起到的作用隨著時間的變化而變化,且這種變化是嚴格遞增的,即近期的評分信息必然比以往的評分信息更具有參考作用.在對項目的評分進行預測過的程中,將越接近當前的數據所賦予的權重更大,忽略了用戶訪問資源的具體時間段以及特殊非正常情況下的數據對預測的影響.顯然,這是不合理的.例如:今年春節是在1月,此時人們會更喜歡看賀歲片,但是春節過后,人們對賀歲片的喜愛程度會歸于常態.如果要對今年2月賀歲片的評分進行預測,顯然去年12月的數據比今年1月的數據更具有參考意義,該被賦予更高的權重.又如:在中國喜慶節日時,人們對恐怖電影的關注程度會急劇下降,如果因為其時間距離預測時段很接近而將此特殊情況賦予很高的權重,來作為其他用戶的推薦標準,顯然會使推薦效果不理想.因此,本文提出一種模糊遞增的概念,認為越靠近當前時刻的評分,其參考作用的走向是波浪式循序上升的.例如,來自電影租賃網站的Netflix電影評分隨時間的變化趨勢如圖1所示,圖1(a)描述了某一部電影其評分隨著時間的推移,在總體上呈上升趨勢;圖1(b)描述了數據集中擁有不同年齡的電影的評分情況,可以看出,年齡越大的電影的評分趨于越高.圖1從兩個不同的角度來反映電影的評分變化規律,即項目的評分總體呈上升趨勢.然而我們發現,該數據集卻存在特殊情況,如圖1(a)中第500天、1000天、1500天等,電影的評分突兀下降.從整個時間戳看,項目評分雖然呈上升趨勢,但卻出現上下波動的現象,并不符合嚴格遞增規律.

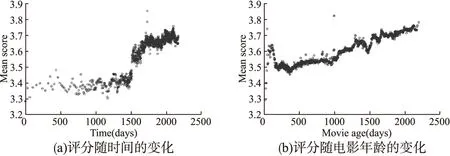
圖1 Netflix數據集電影的評分趨勢Fig.1 Two temporal effects emerging within the Netflix movie-rating dataset

2 相關工作

傳統的協同過濾算法[1-3]存在推薦信息低時效的問題,大多數沒有考慮時間因素的影響,然而時間屬性又是反映用戶興趣規律的重要特性之一,很多學者對此進行了改進.Liu等人[4]提出了一種基于時間的K近鄰協同過濾算法,結合用戶行為的時間信息和K近鄰算法提出了新穎的相似性度量方式.Liang等人[5]提出了Session-based Temporal Graph(STG)算法和Injected Preference Fusion(IPF)推薦算法,刻畫了用戶隨時間變化的偏好.Yan等人[6]在預測過程中引入了時間屬性,提出了一種時分協同過濾算法,并采用不同策略對其進行處理,有效提高了系統的推薦質量.顧亦然等人[7]采用添加時間維度的方式將推薦過程由二部圖遷移到三部圖上進行處理,雖然有效提高了推薦的準確新型,卻在一定程度上增加了算法的復雜度.Gultekin等人[8]提出了一種基于協同卡爾曼過濾的動態模型,解析了用戶/項目的漂移參數隨時間推移的無規則變化.

雖然上述算法考慮到了時間因素在預測過程中的重要性,卻都平等地對其進行評級,忽略了用戶的興趣可能隨時間改變的事實,沒有在預測過程中對時間屬性賦予合適的權重.對此,另外一些學者進行了如下研究,Adibi等人[9]從用戶間相互影響力不同的角度出發,提出了基于用戶時間權重的最近鄰建模方法,有效緩解了批量資源的實時推薦問題,更好地預測用戶評分.為了適應用戶偏好隨時間的動態變化,Ding等人[10]提出了一種時間權重的協同過濾算法,對評分進行時間加權,降低了過時信息的重要性,有效緩解了項目評分老化的問題.Koren等人[11]提出了基于時序的因式分解算法和基于時間變化的基線預測,解析了項目歷史評分信息對當前時刻的瞬時影響和長期影響.An等人[12]提出了基于用戶訪問時間的數據權重和基于加速度的數據權重,并將兩種權重引入協同過濾算法的推薦過程中,動態反映了用戶興趣的變化過程.Hu等人[13]建立了以最新信息為依據的時間序列反饋模型,結合協同過濾實現用戶偏好的動態推薦.為了解析項目歷史評分信息對當前時刻的影響,Zhao等人[14]提出了一種時間分布的協同過濾算法,通過引用時間因子將用戶評分信息劃分不同的時間段,有效緩解了用戶興趣的動態變化問題.Jin等人[15]結合了權重隨時間和項目相似系數,解析了用戶興趣偏好的變化過程.

上述文獻認為用戶的興趣并不是靜態的,而是符合一種遞增規律的,在對數據的處理過程中,雖然考慮到了時間權重的變化,但是都認為數據是嚴格遞增的,即越接近當前的數據對預測的影響越大,忽略了用戶訪問資源的具體時間段以及特殊非正常情況下的數據對預測的影響,這顯然也是不合理的.本文在現有研究的基礎上做出了改進,創新點主要體現在以下方面:1)在計算項目相似度階段引入時間屬性,提出一種基于時間窗口的相似度算法;2)在預測階段,結合權重的模糊遞增提出一種新穎的評分預測算法.3)對于符合模糊遞增的參數,提出一種新穎的多參數優化策略.

3 基于時間窗口的相似性度量

在協同過濾推薦中[16,17],相似性度量用于發現相似的用戶或項目,能否準確發現近鄰用戶或項目,影響推薦結果的準確性.相似性主要是通過基于對象的特征或屬性,利用特征向量間的相似系數、相關系數及距離等來計算.為了反映項目各歷史時期評分的變化規律,本文利用項目評分[18]和項目訪問時間對項目的評分時間劃分時間窗口,并根據時間窗口相似度和鏈式結構度量項目的相似性.

3.1 傳統ItemCF算法

協同過濾算法根據項目特征產生目標用戶的推薦列表,它基于這樣的假設:根據用戶對不同項目的評分存在相似性,需要預測目標項目的評分時,可通過用戶對目標項目的若干近鄰項目進行估計.因此,傳統ItemCF算法[19,20]主要分為兩大階段.

Phase1. Top-K近鄰查找:對于目標項目,需搜尋其近鄰集合,最近鄰數量K可直接給定,即擇取相似性Top-K的項目.近鄰項目主要通過項目相似性進行度量,例如,Pearson相關系數如式(1)所示:

(1)

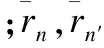
Phase2. 評分預測:近鄰集合產生后,對于目標用戶u尚未評分的項目n,按公式(2)加權計算得到u對n的預測評分Pun,并選擇預測評分最高的若干個項目作為推薦結果反饋給目標用戶.

(2)

3.2 時間窗口相似性

若給定用戶集U=u1,u2,…,uM,則項目n的評分和訪問時間可表示為二元組={,,…,},其中,m≤M,(1≤i≤m)表示ti時刻用戶i對項目n的評分,且t1,尋找與之匹配程度較高的項目.

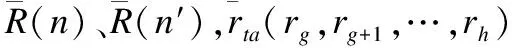
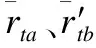
(3)

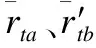
(4)

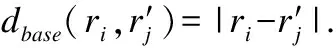
3.3 基于鏈式結構的項目相似性

項目相似度可通過項目之間對應的時間窗口進行衡量.時間窗口的對應關系應滿足兩個條件:一是由于每個時間窗口的評分對項目相似性的度量都起到了一定作用,項目的每個時間窗口皆要有對應關系;二是由于越接近當前時刻的評分對預測所起的作用越大,且項目評分符合遞增規律,項目之間時間窗口的對應關系應按時間順序進行匹配.因此,本文提出基于鏈式結構的項目相似性度量算法.

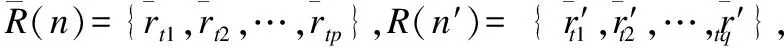
1)若p=q;則項目n、n′的相似度為:

(5)

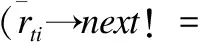
(6)

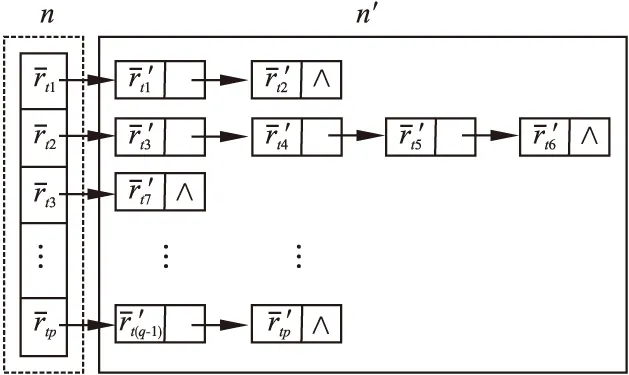
圖2 鏈式法示例Fig.2 Item-based chain structure

Note 1.相似性具有對稱性,D(n,n′)=D(n′,n).

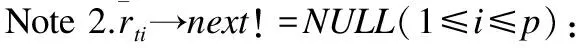
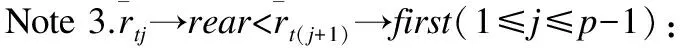
為了使項目相似性得到更好的體現,本文將計算的項目相似度結果規約到(0,1]之間,如式(7)所示.

(7)

4 基于模糊遞增的評分預測

4.1 目標函數構造

隨著時間的推移,項目各歷史時期的評分所起到的作用存在一定的變化規律.因此,我們提出結合時間權重的預測評分公式:

(8)

其中,h(t)的計算方式如式(9)所示.

h(t)=(α1r1+α2r2+…+αmrm)

(9)

s.t.α1+α2+…+αm=1

其中,αi(1≤i≤m,0≤αi≤1)表示歷史時刻ti的用戶評分對當前預測評分起到的作用,即權重大小.

同一用戶對于關聯度較強的項目具有相同的興趣變化趨勢,以單個用戶和單個項目相似集作為計算單位,進行各時期權重的求解.針對每一相似集,采用交叉驗證的方式進行各時期權重序列的求解,每次從相似集中取出一個項目作為測試,并采用平均絕對誤差(mean absolute error,MAE)作為推薦精度的度量標準,如式(10)所示:

(10)

其中,pn表示預測評分,qn表示實際評分,N為測試集大小.顯然,MAE值越小,預測評分效果越佳.因此,各時期權重的求解可用最優化的形式表示,如下式所示:

arg minMAE(α1,α2,…,αm)

(11)

對于目標函數的求解,由于參數之間的關系不明確,較為模糊,難以用普通的參數優化算法進行優化.本文提出一種新穎的多參數最優化的求解策略.由第1節可知,評分與評分的權重的變化存在一定的相似程度.因此,根據評分劃分時間窗口的方式,同樣地對評分權重劃分時間窗口.評分權重(α1,α2,…,αm)可劃分成(βt1,βt2,…,βtz),其中,|βti|稱之為βti的窗口權重,|βti-1|<|βti|(i=1,2,…,tz).因此,對于評分權重的求解可以從全局到局部,即先計算窗口權重,使得窗口權重參數的解達到全局最優,再根據窗口權重與評分權重的關系計算窗口內的評分權重,使得各評分權重達到最優.具體可以分為以下兩個階段,第一個階段是求解符合嚴格遞增關系的窗口權重參數|βti|(i=1,2,…,tz);第二個階段是求解時間窗口內具有隨機波動特性的評分權重參數αi(i=1,2,…,m).

4.2 嚴格遞增參數求解

由于權重序列的時間窗口參數符合嚴格遞增關系,則第一階段中本文通過平均年限法表示各時間窗口的參數關系,如式(12)所示.

(12)

因此,目標函數可表示為:

arg minMAE(βt1,βt2,…,βtz)

(13)

構造拉格朗日函數

(14)

其中β(t)=(βt1,βt2,…,βtz)T,μ1和μ2是拉格朗日參數.

分別對變量βtk、μ1和μ2求偏導:

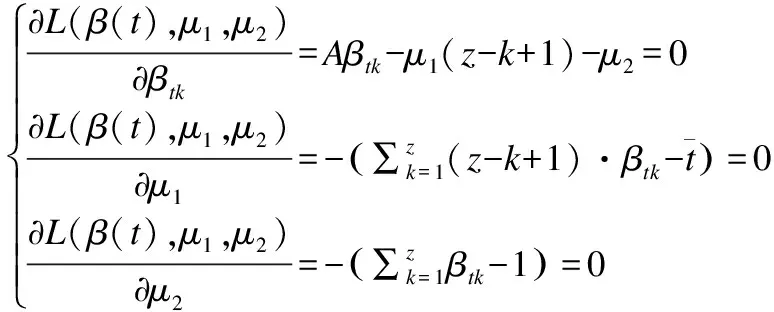
(15)

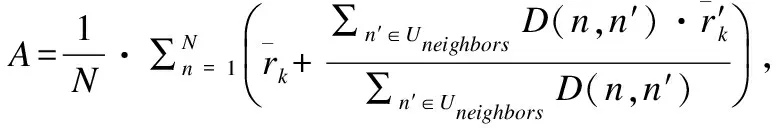
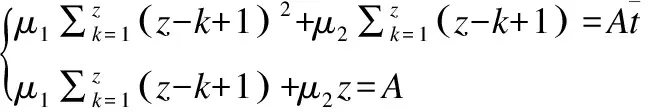
(16)

因此

(17)

tk=t1,t2,…,tz

由于βtk>0,有

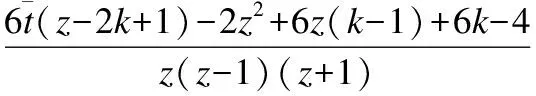
(18)

tk=t1,t2,…,tz

因此

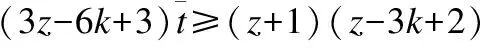
(19)

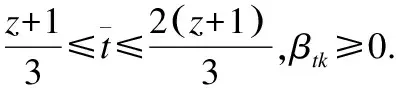
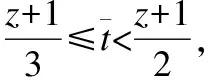
(20)

因此

(21)

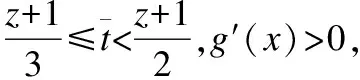
4.3 隨機波動參數求解

針對預測過程的第二階段,本文逐一考慮具有隨機波動性的各個時間窗口內的參數,假設某一時間窗口參數(βtk(αa,αa+1,…,αa+b)),目標函數如式(22)所示.

arg minMAE(βt1,…,βtk-1,αa,αa+1,…,αa+b,βtk+1,…,βtz)

s.tαa+αa+1+…+αa+b=(b+1)βtk

(22)

其中,αi≥0,(a≤i≤a+b).

考慮到粒子群優化算法(Particle Swarm Optimization,PSO)對于多參數的優化具有穩定、高效的性能,本文采用PSO算法[21]來優化窗口內的隨機參數.因此,可以得到單一時間窗口的最優解空間(αa,αa+1,…,αa+b).以此類推,逐一對所有權重求解,可得到權重序列的最優解空間(α1,α2,…,αm).

4.4 算法過程

對于符合模糊遞增規律的參數求解,本文提出了一種新穎的多參數優化策略.以某項目評分時間權重為(α1,α2,…,α10)為例,闡述參數求解的步驟:

1)對時間權重(α1,α2,…,α10)劃分時間窗口,假設劃分結果如下:窗口1包含參數(α1,α2,α3),其中窗口權重與評分權重的關系為βt1=(α1+α2+α3)/3,窗口2包含參數(α4,α5,α6),其中βt2=(α4+α5+α6)/3,窗口3包含參數(α7,α8,α9,α10),其中βt3=(α7+α8+α9+α10)/4,窗口權重βt1<βt2<βt3;

2)利用公式(12)將窗口權重不等式轉化成等式,作為目標函數argminMAE(βt1,βt2,βt3)的約束條件;

3)將公式(13)轉化成標準的拉格朗日函數,分別以βtk(k=1,2,3)、μ1和μ2作為變量進行求偏導;

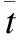
5)利用窗口權重與評分權重的關系,逐一分解窗口權重,通過PSO算法求解目標函數公式(22).

5 實驗結果及分析

為了驗證本文提出的算法有效性,進行了一系列的仿真實驗,主要有以下三個方面:

1)相似度過程中,討論時間窗口的劃分方式以及時間窗口的個數對平均準確率(Mean Average Precision,MAP)的影響,以及比較基于時間窗口的相似性算法(Time Window-based Item Similarity,TWIS)與傳統ItemCF算法的相似性度量算法的推薦精度.

5.1 實驗設計

實驗采用Netflix數據集,含480,189個用戶對17,770部電影的100百萬條評分,時間1999年11月11日至2005年12月31日.隨機抽取5,000部電影作為實驗數據(簡稱NF5M),其中80%作為訓練集,20%作為測試集,Top-K設為30,并采用MAP值作為推薦質量的度量標準(MAP=1-MAE).

表1 NF5M數據集的特點
Table 1 Characteristics of data set NF5M

NameofdatabaseNF5MNumberofusers472542Numberofitems5000Numberofratings5Timespent2001．01．08-2005．12．31

5.2 不同時間窗口劃分方式的MAP對比

本小節分析了不同時間窗口劃分方式對推薦精度MAP值的影響,并與傳統ItemCF進行比較.

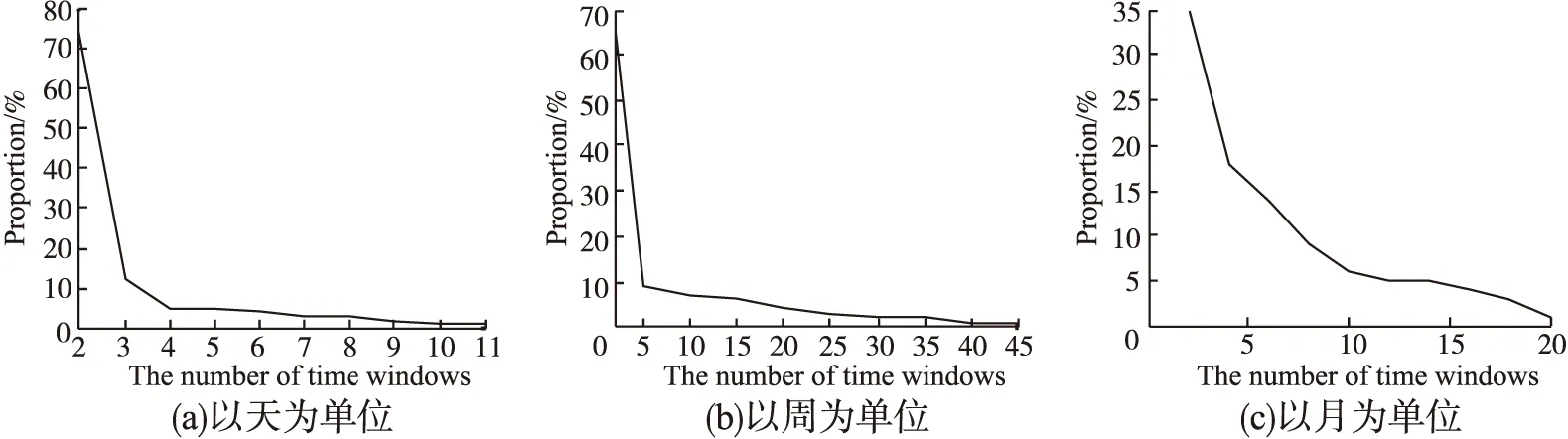
圖3 不同單位的時間窗口劃分Fig.3 Partition time windows in different units

實驗統計,以天為單位,每部電影平均有503天存在評分;以周為單位,每部電影平均有126周存在評分;以月為單位,每部電影平均有36個月存在評分.單位不同,導致評分序列時間窗口劃分的數量也不同.圖3(a)中,由于評分個數較多,較難滿足劃分條件.圖3(b)中時間窗口數達到45,能較好滿足時間窗口劃分的條件.圖3(c)中時間窗口數雖占評分個數的1/2,但時間窗口數量較少.時間窗口數越少,劃分方式就越多,因此,以不同單位劃分時間窗口對窗口數有很大的影響.為了使相似度更加準確,選擇同一時間窗口數中項目之間對應時間窗口的最小距離作為衡量項目相似的基礎.

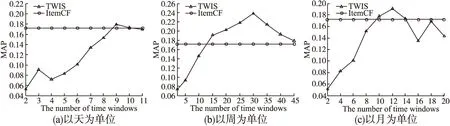
圖4 不同單位的MAP值Fig.4 MAP in different units

圖4中,本文TWDS算法以不同單位劃分時間窗口,并與傳統ItemCF算法對比MAP值.圖4(a)中,隨時間窗口數的增加,MAP值也隨之提高.當窗口數為9時,MAP值達到最高值0.179,比傳統ItemCF算法高0.007.圖4(b)中,當窗口數多于15時,MAP值均高于傳統ItemCF算法,當窗口數為30時,MAP值達到0.238.圖4(c)中,當窗口數多于8時,MAP值在0.172上下波動,與ItemCF算法相差不大.因為,時間窗口數占評分個數的比例較低時,MAP值會較低,所以,時間窗口數較少時,無法描述歷史不同階段評分的變化規律.例如,時間窗口數為2時,MAP均低于0.08.因此,劃分時間窗口的個數對MAP的值有很大的影響,當選擇合適的窗口數時,本文算法的推薦精度均會高于傳統的協同過濾算法.

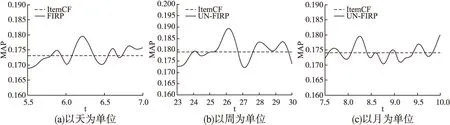
圖5 非模糊遞增值的MAP值Fig.5 MAP of un-FIRP in different units

5.3 不同參數的MAP對比

圖5給出隨機權重與傳統ItemCF預測算法推薦精度MAP值的比較.圖5(a)中隨機權重推薦算法的精度最高為0.179,最低為0.169,與傳統ItemCF預測算法的MAP值相差不大.圖5(b)隨機權重的MAP值最高為0.189,最低為0.172,傳統ItemCF預測算法的MAP值0.179相差0.007.圖5(c)中隨機選取的權重MAP值在0.174上下波動,與傳統預測算法推薦精度差別較小.可以看出,隨機分配的權重與各時期評分權重相等的推薦效果相似.因此,本文算法與傳統ItemCF中預測算法在推薦效果上差別較小.

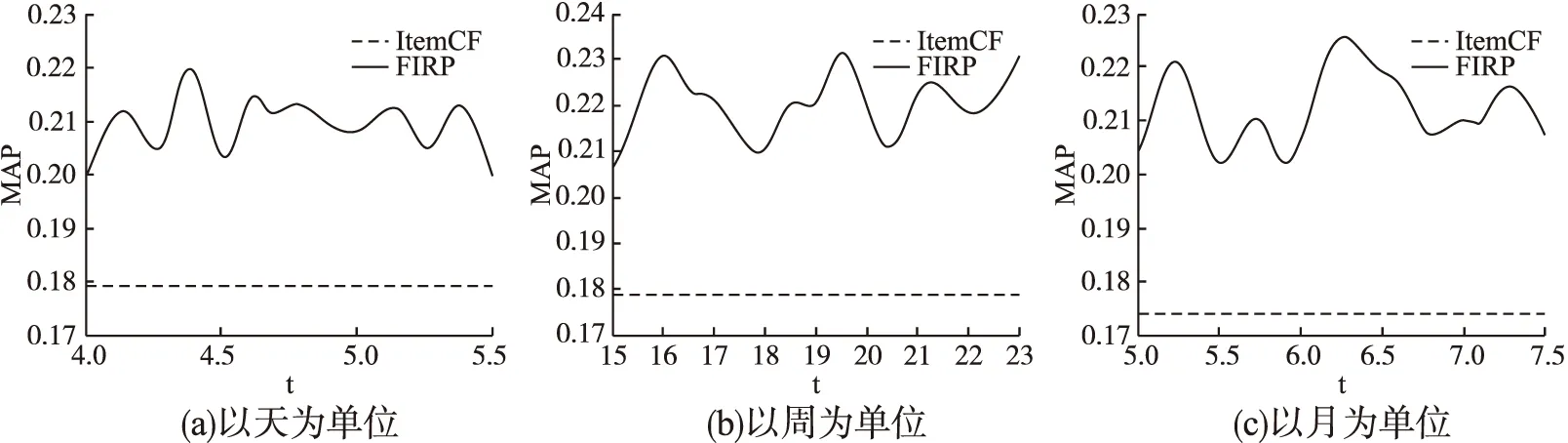
圖6 模糊遞增值的MAP值Fig.6 MAP of FIRP in different units

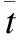
5.4 參數z和的關系及文獻對比

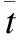
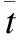
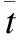
ztMAP15[16/3，8)0．221±0．02220[7，21/2)0．228±0．02325[26/3，13)0．239±0．03230[31/3，31/2)0．251±0．03335[12，18)0．233±0．03140[41/3，41/2)0．225±0．023

圖7對本文FICF算法與文獻[10]TWCF算法、文獻[13]TSFCF算法和文獻[15]TCICF算法進行了對比.文獻[10] TWCF算法認為項目的評分規律符合嚴格遞增的規律,忽略了特殊事件的發生,其MAP的平均值和最大值分別為0.229和0.235;文獻[13] TSFCF算法主要使用時間序列模型,通過最后的事件反饋修正預測值,忽略了歷史各時期的評分規律,其MAP的平均值和最大值分別為0.239和0.271;文獻[15] TCICF算法通過利用了艾賓浩斯的遺忘曲線規律,判斷用戶興趣的遺忘趨勢,但忽略特殊時期的波動性,其MAP的平均值和最大值分別為0.242和0.267;而本文中FICF算法的平均和最高MAP值分別為0.251和0.284,均高于其它三種算法.顯然,本文FICF算法能更好的把握項目評分隨時間推薦的變化趨勢,及為用戶提供更精確的推薦列表.

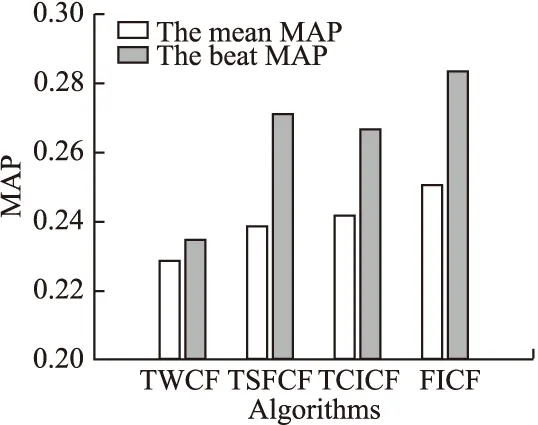
圖7 不同推薦算法的MAP值Fig.7 MAP in different recommended algorithms

6 結 論

本文針對傳統協同過濾數據的靜態性,提出了一種權重遞增的協同過濾算法.在Top-K近鄰的查找階段,利用項目評分的時間屬性提出了一種時間窗口的相似性分析算法;在預測階段,假設權重序列符合模糊遞增的規律,并通過兩階段進行求解.與以往文獻相比,本文更加注重項目評分的時序性以及項目評分隨時間推移的變化趨勢.多組實驗表明,本文算法能更有效的捕捉項目評分的變化規律,為用戶提供更精準的產品參考.

[1] Jiang S,Qian X,Shen J,et al.Author topic model-based collaborative filtering for personalized POI recommendations[J].IEEE Transactions on Multimedia,2015,17(6):907-918.

[2] Zou J,Fekri F.A belief propagation approach to privacy-preserving item-based collaborative filtering[J].IEEE Journal of Selected Topics in Signal Processing,2015,9(7):1306-1318.

[3] Yang H,Ling G,Su Y,et al.Boosting response aware model-based collaborative filtering[J].Knowledge & Data Engineering IEEE Transactions on,2015,27(8):2064-2077.

[4] Liu Y,Xu Z,Shi B,et al.Time-based k-nearest neighbor collaborative filtering[C].IEEE,International Conference on Computer and Information Technology,2012:1061-1065.

[5] Liang X,Quan Y,Shiwan Z.Temporal recommendation on graphs via long- and short-term preference fusion[C].ACM SIGKDD International Conference on Knowledge Discovery & Data Mining,New York,USA,2010:723-732.

[6] Yan Y,Long Y.Notice of retraction collaborative filtering based on time division[C].IEEE International Conference on Computer Science and Information Technology.IEEE,2010:312-316.

[7] Gu Yi-ran,Chen Min.One Tag Time-weighted recommend approach on tripartite graphs networks[J].Computer Science,2012,

39(8):96-98.

[8] Gultekin S,Paisley J.A collaborative kalman filter for time-evolving dyadic processes[C].IEEE International Conference on Data Mining,Shenzhen,China,2014:140-149.

[9] Adibi P,Ladani B T.A collaborative filtering recommender system based on user′s time pattern activity[C].Information and Knowledge Technology,2013:252-257.

[10] Ding Y,Li X.Time weight collaborative filtering[C].ACM CIKM International Conference on Information and Knowledge Management,Bremen,Germany,October 31 - November,2005:485-492.

[11] KOREN Y.Collaborative filtering with temporal dynamics[C].ACM SIGKDD International Conference on Knowledge Discovery & Data Mining,New York,USA,2009:89-97.

[12] An X,Su N.A dynamic filtering recommendation algorithm based on topic[C].International Conference on Electronic and Mechanical Engineering and Information Technology.IEEE,2011:3959-3962.

[13] Hu Y,Peng Q,Hu X,et al.Web service recommendation based on time series forecasting and collaborative filtering[C].IEEE International Conference on Web Services.IEEE,2015:233-240.

[14] Zhao J,Yu X,Sun J.TDCF:time distribution collaborative filtering algorithm[C].International Symposium on Information Science and Engineering.IEEE,2008:98-101.

[15] Jin X,Zheng Q,Sun L.An optimization of collaborative filtering personalized recommendation algorithm based on time context information[J].Advances in Information & Communication Technology,2015,449:146-155.

[16] Li B,Zhu X,Li R,et al.Rating knowledge sharing in cross-domain collaborative filtering[J].IEEE Transactions on Cybernetics,2014,45(5):1054-1068.

[17] Xiao Y,Peng Q A I,Hsu C H,et al.Time-ordered collaborative filtering for news recommendation[J].Communications China,2015,12(12):53-62.

[18] Hu Y,Peng Q,Hu X,et al.Time aware and data sparsity tolerant web service recommendation based on improved collaborative filtering[J].IEEE Transactions on Services Computing,2015,8(5)782-794.

[19] Rafailidis D,Nanopoulos A.Modeling users preference dynamics and side information in recommender systems[J].IEEE Transactions on Systems Man & Cybernetics Systems,2016,46(6)782-792.

[20] Sun Guang-fu,Wu Le,Liu Qi,et al.Recommendations based on collaborative filtering by exploiting sequential behaviors[J].Journal of software,2013,24(11):2721-2733.

[21] Li YL,Shao W,You L,et al.An improved PSO algorithm and its application to UWB antenna design[J].IEEE Antennas and Wireless Propagation Letters,2013,12(3):1236-1239.

附中文參考文獻：

[7] 顧亦然,陳 敏.一種三部圖網絡中標簽時間加權的推薦方法[J].計算機科學,2012,39(8):96-98.

[20] 孫光福,吳 樂,劉 淇,等.基于時序行為的協同過濾推薦算法[J].軟件學報,2013,24(11):2721-2733.