基于Ansys的某型艦炮托架拓撲優化設計

黃觀明，楊宏亮，張建波，劉圣強

(鄭州機電工程研究所，河南 鄭州 450015)

0 引 言

旋回架是某型艦炮的主要支撐結構，其主要由炮床和2個托架組成。2個托架構成U型大耳軸形式，托架耳環對稱安裝左、右高低滾珠座圈的外環，兩者共同作用在垂直面上轉動，保證艦炮裝置進行高低瞄準。托架的主要作用是支撐艦炮搖架、自動機和供彈系統的重力，以及承受艦炮射擊過程中產生的作用力。艦炮總體對各部件的質量都有嚴格的要求，因此在方案設計的過程中需要對托架結構進行優化設計，使得在滿足結構剛度和強度的條件下，托架質量達到最小，進而減輕旋回架的質量，實現輕量化設計的目的。旋回架的結構如圖1所示。

拓撲優化是結構優化設計領域最常用的方法[1]。均勻化法是連續體拓撲優化中應用非常廣泛的一種方法，如果結構的模型、材料特性和載荷工況都不是很復雜的情況下，該方法計算時間短，迭代次數小，且其算法對于所有連續體結構都適用，是一個極為有效的方法[2]。

Ansys提供了以有限元為基礎的結構優化設計功能，可以進行全面的尺寸優化、形狀優化和拓撲優化，為產品設計提供了一個很好的平臺，并在實際工程應用中取得了很好的效果。在產品設計階段，靈活運用各種拓撲優化技術，可以確定材料的最佳分配方案，以便對結構進行改進設計，節約生產成本，實現產品經濟、高效的設計。

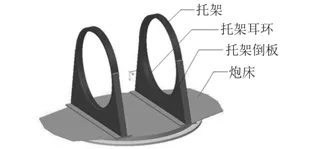
圖1 旋回架結構Fig.1 The structure of cycle frame

1 均勻化法拓撲優化

1.1 均勻化法原理

均勻化方法（Homogenization Method）是一種具有十分嚴密的力學和數學基礎的材料描述方法。它在連續體結構拓撲優化設計的工程運用十分廣泛，并取得了很好的效果。1988年Bendsoe和Kickuchi將結構拓撲優化歸結為材料在一定區域內的優化分布問題，建立了基于微結構概念和均勻化理論的拓撲優化理論，把復雜的拓撲優化問題轉化成廣義上的尺寸變量問題，為拓撲優化的求解提供了一個新思路[3]。它的基本思想是：由微結構的形式和尺寸參數決定宏觀材料的密度和彈性性質出發，在進行優化求解的過程中，把微結構單胞引入組成拓撲結構的材料中，用尺寸固定的孔洞微結構的單胞構造設計區域，并以微結構的單胞尺寸為優化設計變量，把材料密度、彈性模量等參量表示成微結構單胞尺寸變量的函數，通過單胞尺寸的消長來實現微結構的增刪，若孔洞變大到整個微結構，則該微結構消失，即材料被去除，形成偽密度為0的區域。若孔洞變小以致消失，則該微結構被填充，也即材料得以保留，形成偽密度為1的區域。若優化結束時，還存在微結構，則該區域由某種復合材料組成，也即是偽密度在0-1的中間區域。通過此種方法使得結構拓撲優化模型與尺寸優化模型的統一和連續化。

1.2 均勻化法拓撲優化數學模型

根據Bendsoe和Kickuchi提出的均勻化理論和微結構概念，以微結構單胞密度為設計變量，柔順度最小為目標函數，約束條件為體積限定的情祝下，建立均勻化方法的拓撲優化數學模型。其

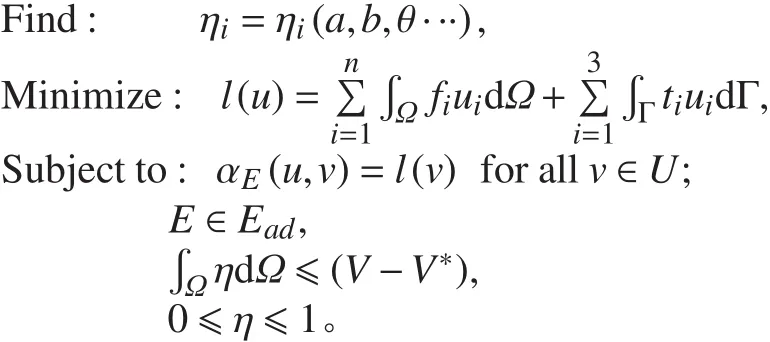
高校擴招政策對城鄉不同收入群體的影響也存在差異。其中，擴招政策對城鄉低收入群體產生的影響表現為對農村50%以下低收入群體收入影響并不顯著，但對城鎮居民50%以下低收入群體產生顯著的正向影響，同時高校擴招政策對城鄉低收入群體教育產生了擴大的“馬太效應”。進一步地，可以發現農村居民高收入組的教育回報率為6.9%，高于城鎮居民的4.1%，結合擴招政策對城鄉居民教育回報和收入回報的影響可以發現，高校擴招政策導致城鄉居民高收入群體組的教育差距擴大，但在一定程度上縮小了高收入群體城鄉間的收入差距。

采用均勻化方法求解撲拓撲優化問題，一般分為3 個步驟[4]：

①復合材料力學為基礎，由最小勢能原理出發并結合均勻化理論的微元體假設，并由公式

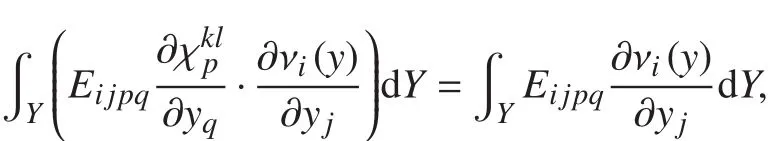
得到材料特征參數χkl。然后利用公式

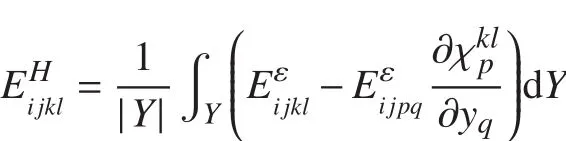
②用有限元方法求解結構位移場和其他性能指標。

③采取一定的優化算法更新設計變量，并保證計算過程的穩定性和收斂性。

2 基于Ansys的托架拓撲優化分析

2.1 基于Ansys的拓撲優化

Ansys軟件的拓撲優化技術采用的是均勻化方法。主要過程為：首先在每個有限元單元內構造微結構單胞，微結構的形式和尺寸決定了單元的彈性性質和密度；優化過程中，以微結構的單胞尺寸作為拓撲優化設計變量，以單胞尺寸的消長實現微結構的增刪；經過多次迭代計算，結構中產生不同尺寸的孔洞，從而達到拓撲優化之目的[6]。

Ansys的拓撲優化不需要人為去定義優化參數，而是自動將材料分布當作優化參數。在進行拓撲優化分析時，同其他有限元分析一樣定義幾何結構、有限元模型、施加載荷和邊界條件等，然后定義優化分析的目標函數，從而定義約束參數。拓撲優化的目標即目標函數是在滿足給定的實際約束條件下（如體積減小等）需要極大或極小的參數，通常采用的目標函數是結構柔順度極小化或基頻最大等[7]。

Ansys進行拓撲優化的一般過程為：

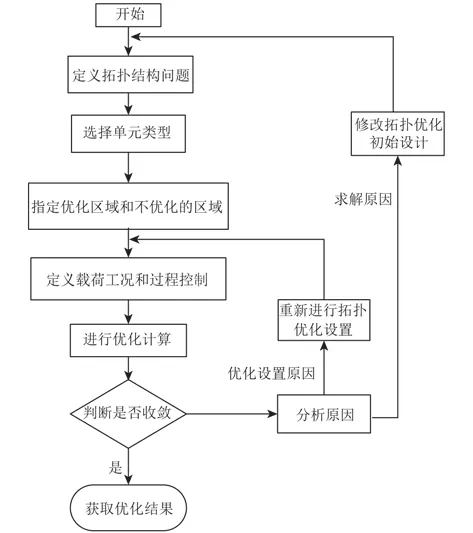
圖2 Ansys拓撲優化流程圖Fig.2 Topology optimization flow chart of Ansys

2.2 拓撲優化前處理

托架的設計優化區域為托架的側板部分。如圖3所示，區域1（耳軸、底板）為不優化的區域，區域2（側板）為優化區域。從PROE中導入托架的三維模型，設定單元尺寸為20 mm，對托架用六面體劃分網格。托架所用材料為鋁合金材料7A52，其相關參數如表1所示。

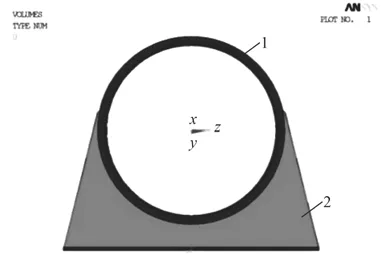
圖3 托架優化區域與不優化區域Fig.3 Optimized area and not optimized area

表1 7A52材料特性Tab.1 The material characteristics of 7A52

優化計算時考慮水平射擊和垂直射擊2種工況，2種工況基本涵蓋了托架的正常使用受力情形。計算中的載荷為火炮射擊最大后座力160 kN，載荷以軸承載荷的方式平均加到兩側托架的耳軸內環面上，因此每個托架承受載荷為80 kN，計算中約束加在底板的底面。

2.3 拓撲優化求解

利用Ansys的參數化語言對托架進行拓撲優化求解控制，其命令流如下：

TOCOMP，MOCOMP，MULTIPLE，2

！將多柔度MOCOMP（考慮2個載荷工況）定義為拓撲優化函數

TOVAR，MOCOMP，OBJ

！將MOCOMP定義為目標函數。

TOVAR，VOLUME，CON，80

！定義約束函數VOLUME，約束條件為體積縮小80%。

TOTYPE，OC

！選用OC方法進行拓撲優化求解

TODEF，0.00001！定義優化收斂精度為0.0001

TOLOOP，50，1！自動進行50次優化迭代計算

2.4 拓撲優化后處理

1）托架結構的節點和單元偽密度云圖如圖4和圖5所示（2色顯示）。圖中區域1的偽密度值為1，表示該區域的材料應該保留。區域2的偽密度值為0，表示該區域的材料應該被去除。通過偽密度云圖，可以得到托架結構材料的最佳分配和托架結構改進的大致方案。

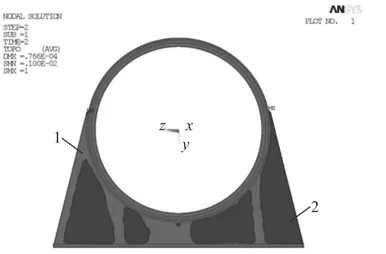
圖4 托架的節點偽密度云圖Fig.4 Node false density plot of bracket

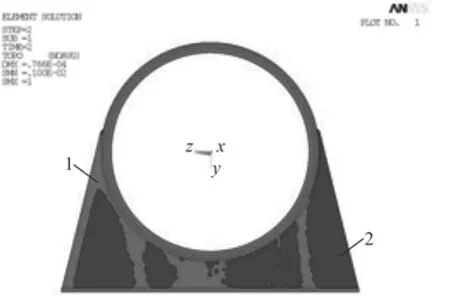
圖5 托架的單元偽密度云圖片Fig.5 Element false density plot of bracket

2）托架的目標函數和約束函數迭代曲線如圖6和圖7所示。目標函數迭代曲線表明，在迭代計算的過程中托架結構柔順度的變化趨勢情況，托架經過27次迭代收斂，結構柔順度由最初的13.481 N·m逐漸減為6.012 N·m。約束函數的迭代曲線表明，在迭代計算過程中體積的變化趨勢情況，迭代過程中體積始終在8.96×10–3m3附近波動，最后趨于穩定，與最初托架的體積4.39×10–2m3相比，體積減小了80%。

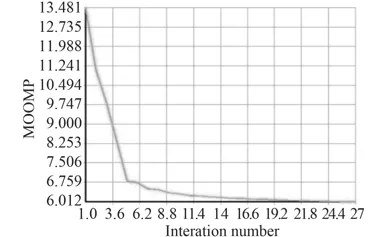
圖6 目標函數迭代曲線Fig.6 Iterated curve of objective function

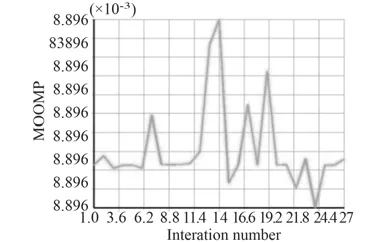
圖7 約束函數迭代曲線Fig.7 Iterated curve of constraint function

3 托架結構可制造化改進

因拓撲優化設計只是一種概念設計，其優化結果極不規則，不便于加工和制造，所以必須對優化結果進行可制造化處理。根據圖4和圖5中的拓撲優化結果，左邊深色部分為密度值為0的區域，對其進行挖孔處理，淺色部分為材料堆積的位置，對其進行適當延寬并加肋。結合制造工藝，建立托架的新結構如圖8所示。對改進后的托架結構進行有限元靜力分析，其改進前后結構的相關參數對比如表2所示。

從表2的比較結果可以看出改進后的結構在質量減少16%的情況下，托架結構最大應力基本沒有變化，最大變形減少了15%。且托架用所用鋁合金材料為7A52，其屈服極限在255 MPa以上，優化后的結果滿足了強度、剛度性能的要求，達到了結構輕量化設計的目的。

圖8 改進后的托架結構Fig.8 The improved bracket structure

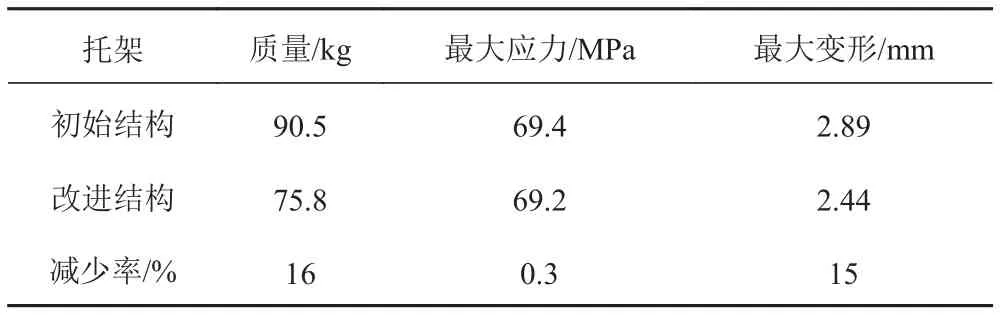
表2 改進前后托架相關參數對比Tab.2 Comparison of the relevant parameters before and after improvement

4 結 語

本文運用拓撲優化中的均勻化理論，通過Ansys軟件提供的拓撲優化功能，對某型艦炮托架進行了拓撲優化研究，解決了以往按經驗設計的局限。經過拓撲優化設計改進后的托架與初始結構相比，托架結構質量減少了16%，最大應力基本沒有變化，最大變形減少了15%，實現了托架輕量化設計的目的，證明拓撲優化設計的可行性。這對于艦炮結構改進設計具有工程應用價值，對其他一般機械結構問題也提供了一種設計思路。

[1]曹德樂.基于拓撲優化的發罩內板筋條結構正向設計[J].裝備制造技術, 2015, (5): 111–114.

[2]孫蓓, 蘇超.拓撲優化均勻化方法的改進迭代算法[J].河海大學學報, 2010, 38(1): 47–51.

[3]王明強, 徐健.基于均勻化法的風雨載荷下折疊式艙口蓋拓撲優化設計研究[J].船舶工程, 2014, 36(1): 10–13.

[4]左孔天, 陳立平, 鐘毅芳, 等.基于人工材料密度的新型拓撲優化理論和算法研究[J].機械工程學報, 2004, 40(12): 31–37.

[5]左孔天.連續體結構拓撲優化理論與應用研究[D].武漢: 華中科技大學, 2004: 17–20.

[6]胡松, 黃勇, 陳波, 等.基于石膏空腔模的無梁樓蓋拓撲優化及拓撲結構靜力特性研究[J].空間結構, 2015, 21(1): 54–63.

[7]博弈創作室.ANSYS9.0經典產品高級分析技術與實例詳解[M].北京: 中國水利水電出版社.