幾種堆石料雙曲線模型參數整理方法的比較

侯偉亞，張兆省，張幸幸，皇甫澤華，鄧 剛，溫彥鋒

(1.中國水利水電科學研究院流域水循環(huán)模擬與調控國家重點實驗室，北京 100048；2.河南省前坪水庫建設管理局，河南 鄭州 450003)

0 引 言

雙曲線模型是土石壩應力變形分析中應用較廣的一類本構模型。1963年，康德等[1]提出用雙曲線擬合土體常規(guī)三軸試驗中偏差應力和軸向應變的關系，即

(1)

式中，a、b為試驗常數；(σ1-σ3)為偏差應力；εa為軸向應變。

鄧肯等[2-3]在此雙曲線關系的基礎上提出了目前廣泛應用的鄧肯-張E-v及鄧肯E-B增量彈性模型。沈珠江等[4]建議的雙屈服面模型中，仍建議用雙曲線來擬合常規(guī)三軸試驗條件下的(σ1-σ3)～εa關系。高蓮士等[5]建議在非線性解耦K-G模型中，假定常規(guī)三軸剪切試驗中應力比與剪應變之間存在雙曲線關系。以上幾種本構模型可統(tǒng)稱為雙曲線模型。雙曲線模型的顯著優(yōu)點是參數可以通過常規(guī)三軸試驗測定，物理意義明確，易于接受，因而在國內外土石壩的靜力變形分析中得到廣泛采用[6]。

合理確定本構模型參數對土石壩應力變形分析結果的合理性有著至關重要的影響[7]，許多研究[8-11]都圍繞合理確定土石壩筑壩材料的本構模型參數展開。在土石壩工程實踐中，常用的雙曲線模型參數a、b的整理方法主要有兩種：一種是直線擬合法，將縱坐標軸變換為εa/(σ1-σ3)，對εa/(σ1-σ3)～εa的試驗點據進行直線擬合，可得b為直線的斜率，a為直線的截距；另一種是鄧肯等[2]提出的兩點法，在εa/(σ1-σ3)～εa坐標系中，過偏差應力為70%和95%抗剪強度的數據點做直線，該直線的截距、斜率分別為a、b。SL237—1999《土工試驗規(guī)程》[12]中建議用后一種方法來推求鄧肯E-B模型的參數；DLT 5355—2006《水電水利工程土工試驗規(guī)程》[13]則未對上述兩種方法做傾向性規(guī)定。在實踐中，對于同一種土石壩筑壩材料，這兩種方法求得的雙曲線模型參數通常是不同的；國內一些研究者對兩種方法進行了比較，對于不同類型的土往往得出不同的結論[14-15]。還有一些研究者提出了新的參數整理方法，如朱俊高等[8]、陳力宏等[16]建議對一組三軸試驗結果進行反演，這一方法實際應用難度較高，由于反演策略的不同有時難以求得唯一解，同時，反演得到的參數只代表數值上的最優(yōu)解，并不一定符合其物理意義[17-18]；劉大康等[19]認為，堆石壩工程中堆石體的實際應變是比較小的，在整理參數時應該更加注重對小應變數據點的擬合，提出將鄧肯的兩點法中，過偏差應力為70%和95%抗剪強度對應的數據點，改為過偏差應力為50%和70%抗剪強度對應的數據點來做直線。

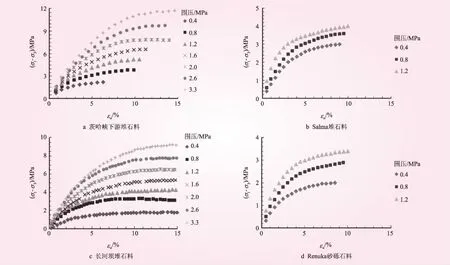
圖1 典型堆石料的三軸試驗結果

筆者認為，直線擬合法或兩點法是限于過去的計算條件、從簡便的角度出發(fā)提出的，在計算機技術已經非常發(fā)達的今天，完全可以采用曲線擬合法，借助有關軟件直接對試驗點據進行曲線擬合來獲取雙曲線模型參數的最優(yōu)解，該方法更為便捷。

本文以鄧肯模型為例，采用4種方法(直線擬合法，鄧肯等建議的兩點法，劉大康等建議的兩點法，曲線擬合法)分別整理幾種典型堆石料的鄧肯-張模型參數K、n、Rf，并比較采用不同參數整理方法時模型預測結果與試驗結果的誤差。在此基礎上，探討不同雙曲線模型參數整理方法優(yōu)缺點和適應性。

1 分析過程簡述

1.1 典型堆石料的試驗曲線和強度參數

本文對文獻[19-21]中4座典型土石壩工程中壩殼料的典型試驗結果(如圖1所示)進行分析，其中茨哈峽、Salma和長河壩均為爆破堆石料的試驗結果，Renuka壩為砂礫石料的試驗結果。

堆石料和砂礫石料的抗剪強度均可用Leps等[22]建議的公式進行描述，即

φ=φ0-Δφ(σ3/pa)

(2)

式中，φ為圍壓為σ3時的內摩擦角；pa為標準大氣壓；σ3為圍壓；φ0和Δφ為非線性強度指標。

4種堆石料的強度指標列于表1。已知強度指標，則可以求得任意圍壓下σ3的抗剪強度。即

(3)

式中,(σ1-σ3)f、σ3為圍壓；φ為圍壓為σ3時的內摩擦角。

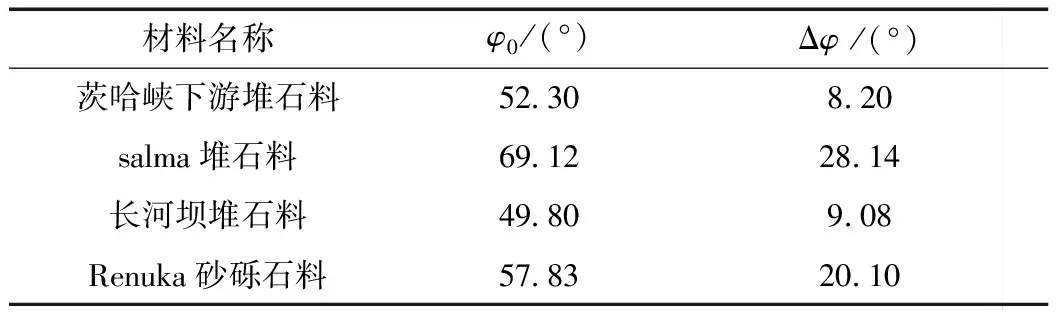
表1 4種堆石料的強度指標

1.2 模型參數的確定

對圖1所示的4組試驗數據分別通過下述4種方法來整理試驗常數a、b。

(1)直線擬合法。將所有試驗數據點繪在εa/(σ1-σ3)～εa坐標系中，通過Excel軟件進行直線擬合，通過Slope函數求取斜率b，通過Intercept函數求取截距a。

(2)鄧肯的兩點法。在試驗數據系列中，選取偏差應力最接近70%(σ1-σ3)f和95%(σ1-σ3)f的兩個試驗點據，過這兩點做直線，直線的截距為a，斜率為b。

(3)劉大康的兩點法。在試驗數據系列中，選取偏差應力最接近50%(σ1-σ3)f和70%(σ1-σ3)f的兩個試驗點據，過這兩點做直線，直線的截距為a，斜率為b。

(4)曲線擬合法。在(σ1-σ3)～εa坐標系中，通過Origin軟件進行雙曲線的曲線擬合，直接確定參數a、b。

求得不同圍壓下的試驗常數a、b后，根據鄧肯等建議，通過式(4)、(5)求取不同圍壓下的初始剪切模量Ei和應力比Rf。即

Ei=1/a

(4)

Rf=b(σ1-σ3)f

(5)

取各個圍壓下平均的Rf作為該土料的Rf；將不同圍壓下的Ei/pa和σ3/pa繪制在雙對數坐標中進行直線擬合，可以得到直線的斜率對應參數n，截距對應參數K。至此，可以求得鄧肯模型的3個重要參數K、n和Rf。

對于本文提到的4種典型堆石料的試驗結果，通過4種不同的方法整理參數a、b，進一步求得鄧肯模型的參數K、n和Rf，結果列于表2，可知不同的參數整理方法對求得的參數值有顯著影響，對于茨哈峽下游堆石料，不同參數整理方法得到的參數K可相差60%以上，n可相差超過100%，Rf的差異稍小，但也接近20%。

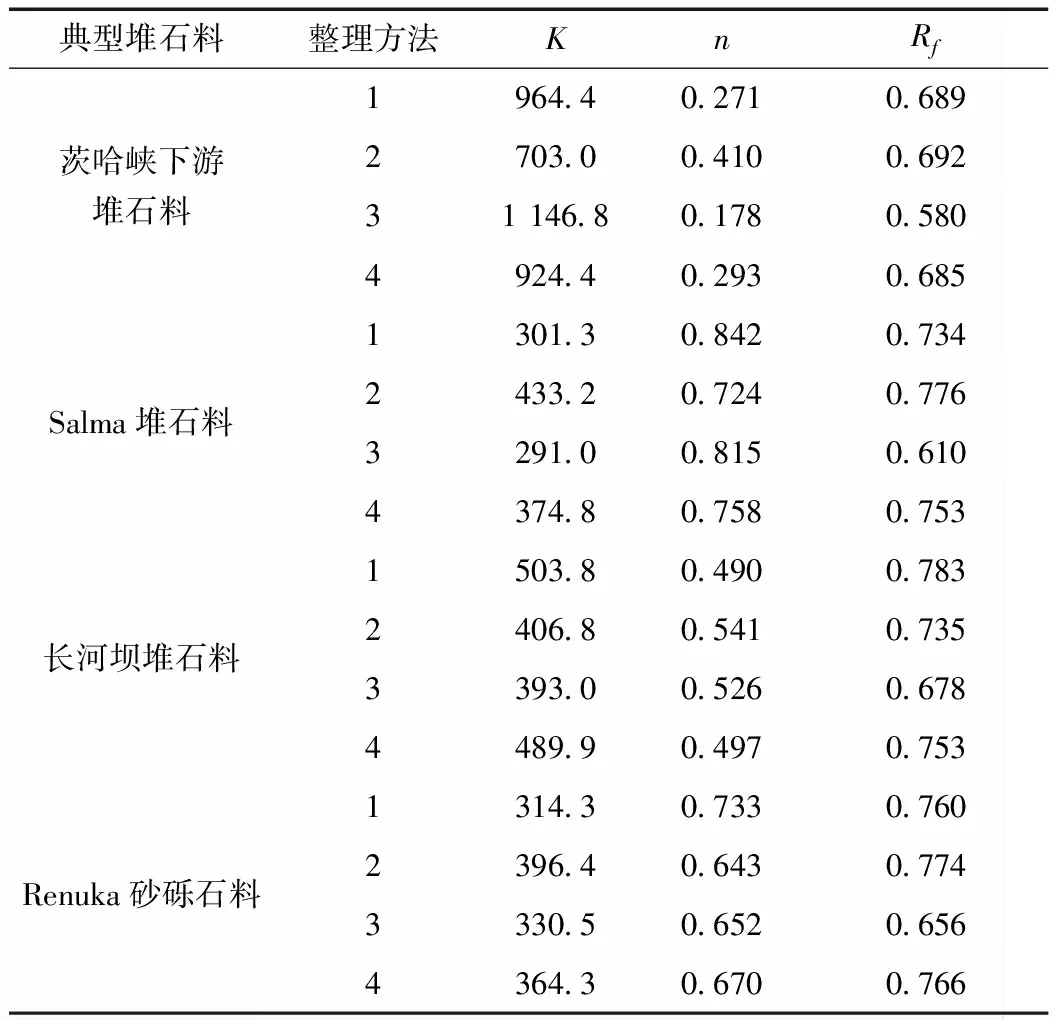
表2 不同方法整理得到的K、n和Rf

1.3 誤差分析

求得鄧肯模型參數K、n和Rf，可以推算任意圍壓σ3下堆石料的偏差應力-軸向應變關系曲線，即

(6)

一般情況下，模型表現與試驗不可能完全一致，式(6)推算的曲線與試驗曲線不可避免的存在一定的偏差。圖2給出了采用不同參數整理方法時，茨哈峽下游堆石料試驗點據與計算應力應變曲線的對比情況。

為了評價模型推求結果與試驗結果之間偏差，定義如下的誤差函數

(7)

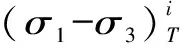
為了便于分析，將表2所列幾種堆石料不同方法求取參數對應的誤差函數F以折線圖的形式繪制在圖3和圖4中。由于Renuka砂礫石料的誤差函數整體上比堆石料要小一個數量級左右，為了便于觀察，將Renuka砂礫石料和其他3種堆石料分開繪制。圖3是考慮所有試驗點據的條件下，模型推求結果與試驗結果之間的誤差函數值。大量的計算分析結果表明，堆石壩壩殼的壓縮應變很少超過5%，因此圖4繪制了只考慮軸向應變小于5%的試驗點據時的誤差函數F。

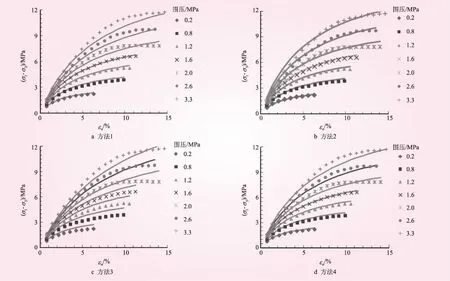
圖2 茨哈峽下游堆石料試驗和計算應力-應變關系對比

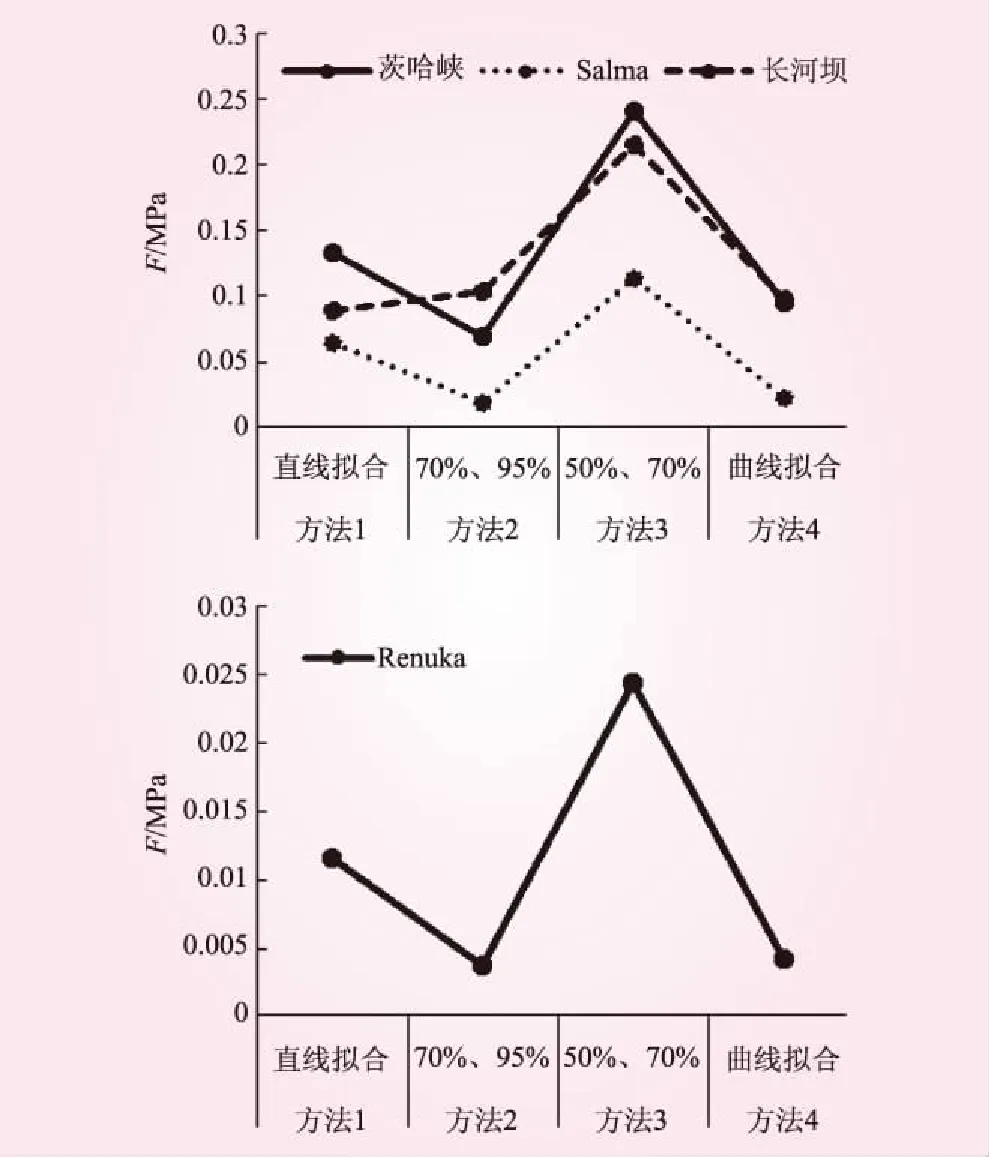
圖3 誤差函數F與參數整理方法的關系(所有試驗點據)

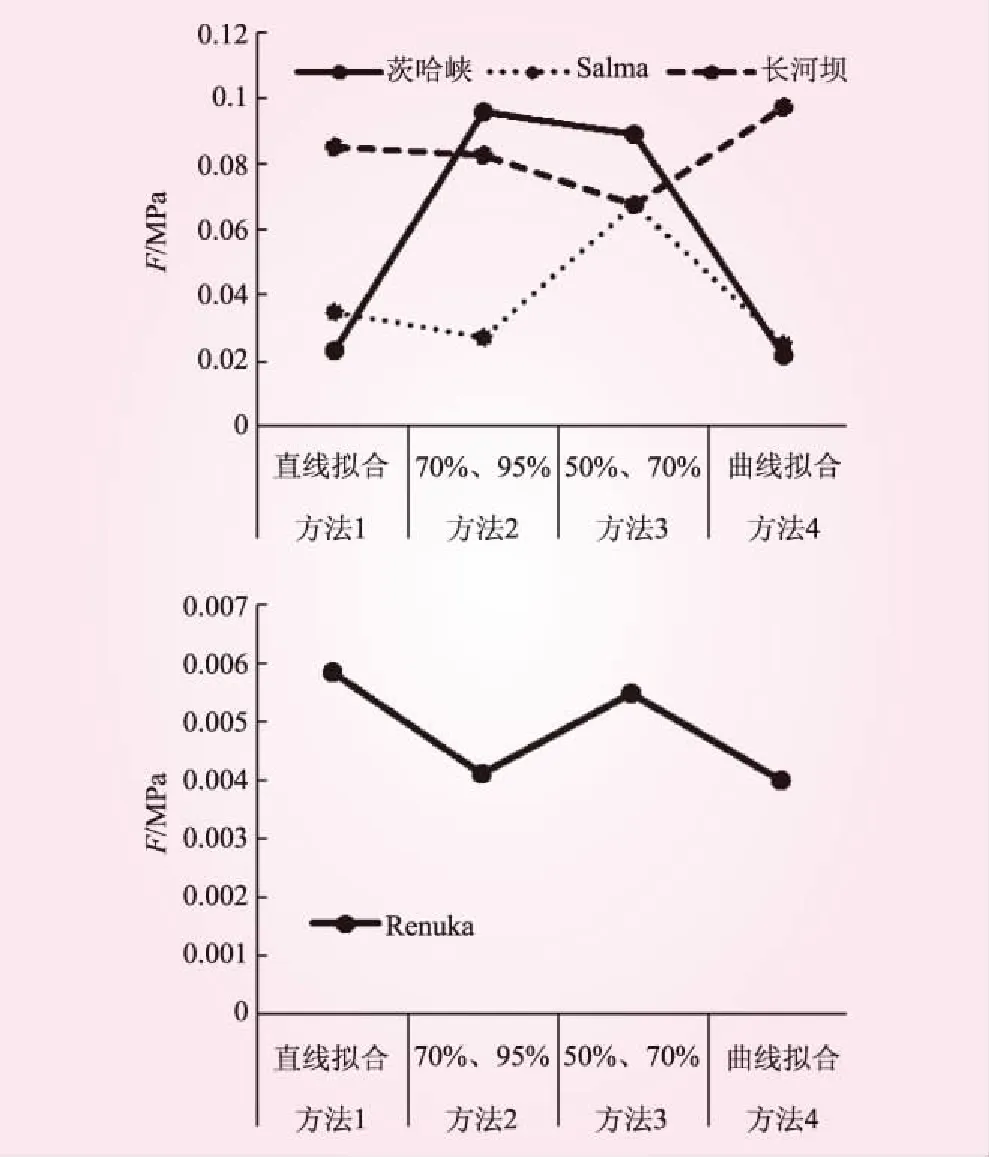
圖4 誤差函數F與參數整理方法的關系(應變小于5%時)

從圖3可以看到，4種材料采用曲線擬合法及鄧肯的兩點法推求參數的誤差函數值F最小；采用劉大康的兩點法推求參數的誤差函數值F最大。從圖4可知，僅考慮軸向應變小于5%的試驗點數據時，對不同材料，參數整理方法對誤差的影響規(guī)律不甚一致。對茨哈峽，鄧肯的兩點法和劉大康的兩點法求得參數的誤差函數值F明顯大于直線擬合法和曲線擬合法，對Renuka砂礫石料，采用直線擬合法和劉大康的兩點法整理參數的誤差稍大。綜合來看，采用曲線擬合法整理參數的誤差較小。

2 討 論

2.1 模型預測與試驗數據之間誤差的來源

本文中誤差函數F表征了模型預測曲線與試驗點據之間的偏差，這與一般曲線擬合誤差的含義不同，實際上包含了兩個層面的誤差。一是整理試驗常數a、b的過程產生的誤差，由于曲線擬合本身就是求使得單條曲線誤差函數F最小的參數，從理論上即可直接推斷“曲線擬合法”的誤差最小；二是通過a、b求鄧肯模型參數K、n和Rf的過程產生的誤差。一般而言，不同圍壓下求得的Rf并不一致，只能取平均值作為材料的Rf，lg(Ei/pa)和lg(σ3/pa)通常也并不嚴格地符合直線關系，只能通過直線擬合求得K和n，這一過程會產生新的誤差。圖5以茨哈峽下游堆石料為例，反映了這一現象。理論上，第二個層面的誤差與參數整理方法沒有直接聯(lián)系。在整理本文所述幾種堆石料的參數時發(fā)現，對于茨哈峽下游堆石料，采用兩點法整理參數時，不同圍壓下確定的Rf差異較大，lg(Ei/pa)和lg(σ3/pa)的關系偏離直線關系也較明顯(如圖5和圖6所示)；對于其他3種堆石料，4種整理方法在第二個層面的誤差上沒有顯著差別。

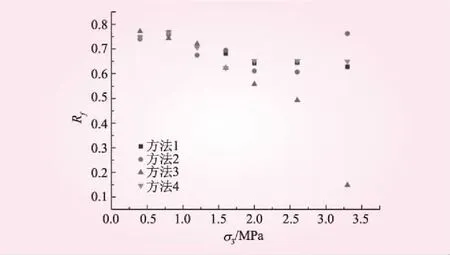
圖5 茨哈峽下游堆石料Rf與 σ3和參數整理方法的關系

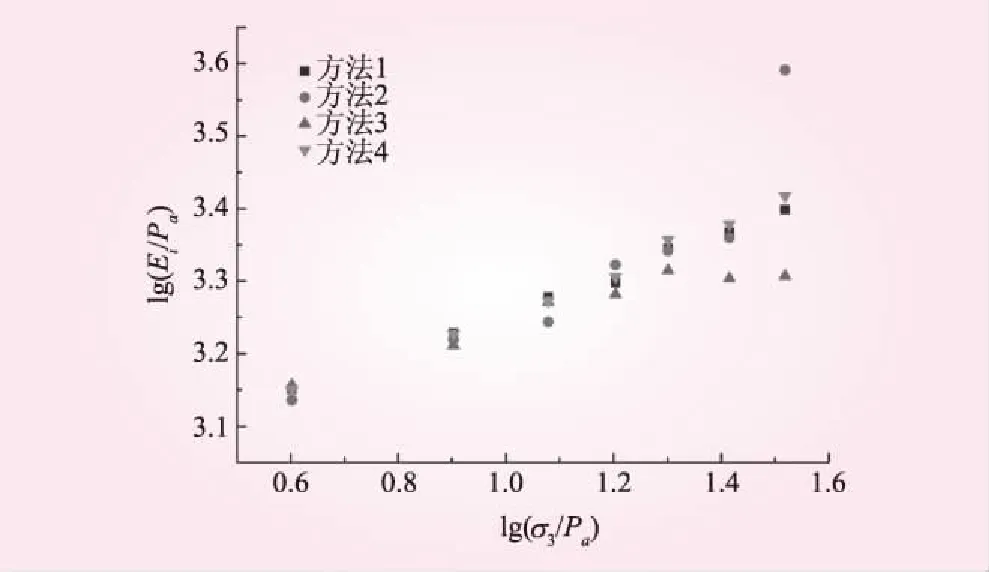
圖6 茨哈峽下游堆石料lg(Ei/pa)與lg(σ3/pa)和參數整理方法的關系

2.2 直線擬合法和兩點法的對比

在求取堆石料雙曲線模型參數的實踐中，小應變條件下εa/(σ1-σ3)～εa點據偏離直線段，是一種比較常見的現象，此時，如果對所有的數據點進行直線擬合，則擬合直線受起始段數據點的影響較大，偏離試驗曲線的直線段。因此，鄧肯等建議采用偏差應力為70%(σ1-σ3)f和95%(σ1-σ3)f的兩個試驗點據的連線來代替擬合直線，該方法能較好的回避試驗曲線起始段偏離直線段的問題。一些研究者提出改變這兩個點的位置，取偏差應力更小的數據點(如偏差應力為抗剪強度的50%和70%)來做直線，以期提高對小應變條件下應力應變關系的擬合精度。從本文的誤差分析結果來看，這種方法收效不佳。圖7以Salma堆石料為例做出說明。對于0.4 MPa圍壓下的試驗點據，由于起始段偏差較明顯，擬合直線偏離試驗曲線的直線段；偏差應力為70%(σ1-σ3)f和95%(σ1-σ3)f的兩個試驗點據的連線與試驗曲線的直線段符合較好；偏差應力為50%(σ1-σ3)f和70%(σ1-σ3)f的兩個試驗點據恰好跨越試驗曲線的拐點，過這兩點的直線與試驗曲線有較大程度的偏離。

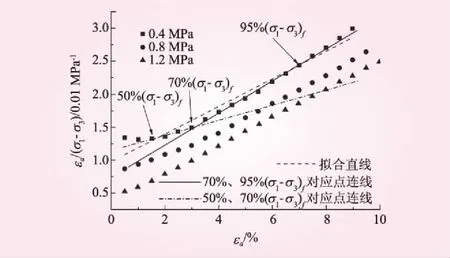
圖7 Salma堆石料的參數整理方法對比

2.3 曲線擬合法的優(yōu)勢

對本文討論的4種堆石料而言，采用鄧肯等建議的兩點法或者曲線擬合法整理雙曲線模型參數，均可使鄧肯模型的預測值與試驗值的誤差較小。但對一些特殊問題，曲線擬合的靈活性更強。

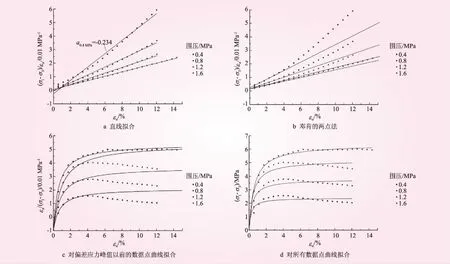
圖8 九甸峽墊層料的三軸試驗結果和參數整理方法對比

圖8給出了一種細堆石料(九甸峽面板堆石壩墊層料)的一組三軸試驗結果，在εa/(σ1-σ3)～εa坐標系中部分試驗右端上翹的趨勢。對于這種情況，如果對所有數據點進行直線擬合，則可能會出現截距(初始模量的倒數)為負的情況；如果僅對偏差應力峰值以前的數據點進行直線擬合或采用兩點法，則會出現不同圍壓下擬合直線截距非常接近(此時n≈0，即材料幾乎沒有壓硬性)、擬合直線偏離大部分試驗數據點的情況。無論哪種情況，均與鄧肯模型參數的物理意義不甚相符。曲線擬合可以根據需要，僅對峰值以前的數據點擬合(圖8c)或者對整條試驗曲線進行擬合(圖8d)。結合一些研究者的建議，模型參數確定應更注重對小應變下堆石料的應力應變數據的擬合，也可采用曲線擬合法來處理，自定義擬合數據點的范圍。

3 結 論

本文對雙曲線模型參數整理方法進行了探討。結合4種典型堆石料的三軸試驗結果，比較了采用4種不同的參數整理方法時，模型預測結果與試驗結果之間的誤差。在此基礎上，對不同參數整理方法的優(yōu)缺點進行了分析，得到主要結論如下：

(1)對于對應力-應變規(guī)律與雙曲線符合較好的堆石料而言，采用鄧肯的兩點法或曲線擬合法都可使鄧肯模型預測結果與試驗結果之間的誤差較小；采用直線擬合法或劉大康的兩點法時，參數整理結果易受到試驗曲線起始段偏離直線關系的影響，導致模型預測結果與試驗結果之間的誤差較大。

(2)僅從堆石料模型預測和試驗結果的誤差而言，鄧肯的兩點法和曲線擬合法都可以較好的控制誤差，但曲線擬合方法具有更好的適應性和靈活性，對于一些特殊情況，傳統(tǒng)方法受到較大限制時，曲線擬合也可較好地解決問題。