自適應與附加動量BP神經網絡的ECT流型辨識

王莉莉　劉洪波　陳德運　馮其帥

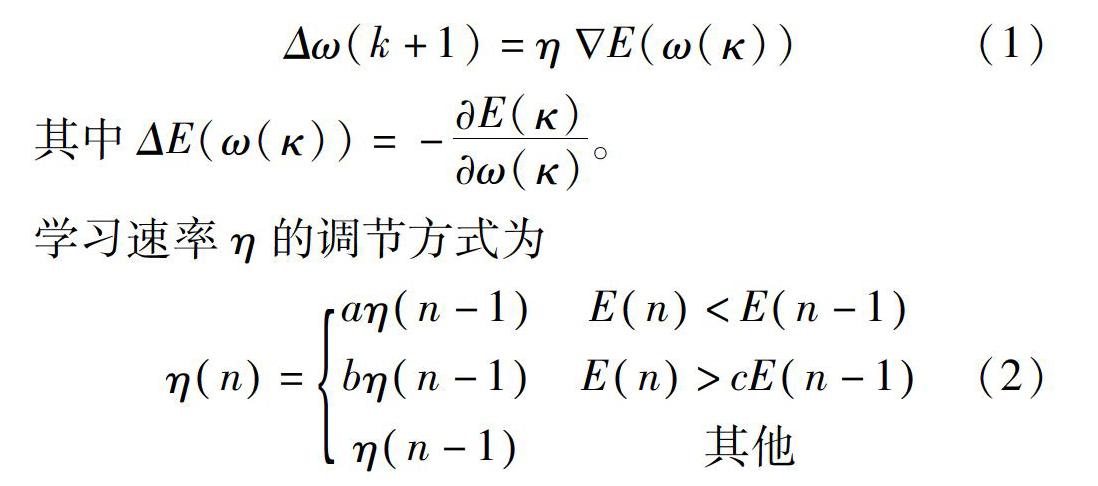
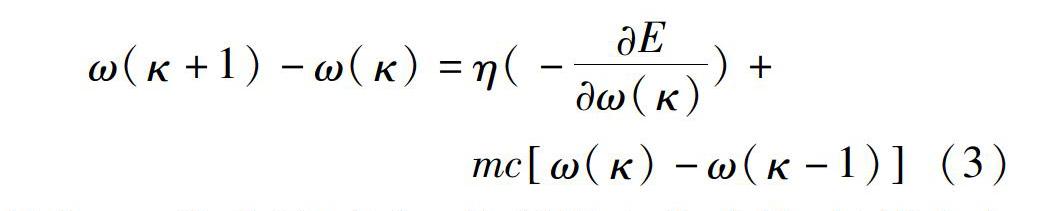
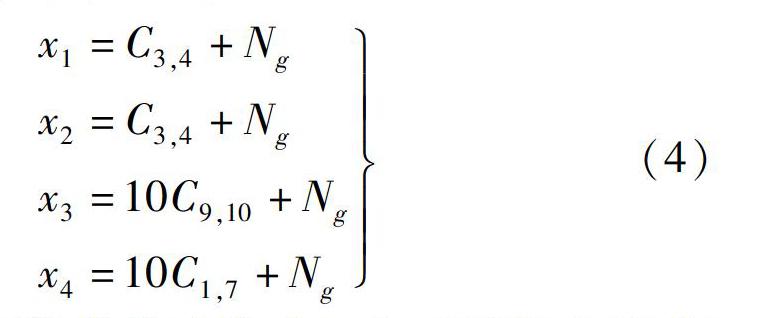
摘要：傳統BP神經網絡是解決電容層析成像系統流型辨識經典的算法，雖然在一些簡單問題上達到了工業實際應用的要求，但如果解決復雜工業問題時就會暴露出很多缺陷。針對傳統BP神經網絡算法的不足，為降低誤差震蕩現象，引入了自適應調節學習速率和附加動量因子。通過輸入電容值進行訓練，得到適合流型識別神經網絡。仿真實驗結果表明，該算法不僅繼承傳統BP神經網絡的優點，而且還提高了ECT系統流型辨識中的收斂速度慢，解決了容易陷入局部極小值的問題。

關鍵詞：電容層析成像；流型辨識；BP神經網絡；局部極小值；收斂速度

DOI：10.15938/j.jhust.2018.01.019

中圖分類號： TP391.9

文獻標志碼： A

文章編號： 1007-2683（2018）01-0105-06

Abstract：Traditional BP neural network is a typical mehtod to solve ECT system of flow pattern identification. It is applied to the simple problems in industrial applications， but there are many defects in solving complex industrial problems. In this paper based on the analysis of deficiency of BP neural network， for reducing the error oscillation， the adaptive learning rate adjustment factor and the additional momentum is introduced. In this method， the electrical capacitance values are input to train a network to identify the flow patterns. The simulation results show the algorithm not only inherits the advantages of traditional BP neural network， but also improve slow convergence and solve being prone to fall into local minimum problems in flow pattern identification of ECT system.

Keywords：electrical capacitance tomography；flow regime identification；BP neural network；local minimum；convergence speed

0引言

流型[1-2]的概念是兩相流過程中的兩相分布狀態，即流體[3]流動的形成。流型辨識的研究對工業發展起到了至關重要的作用。流型辨識方法經過多年研究，雖然取得了一定的成果，但是，在關于流型的技術上還存在同一名稱的流型定義不一致的問題。早期對流型的劃分比較簡單，研究也停留在表面，后期隨著對流型的認識加深以及研究工作的不斷深入，人們開始對流型進行更加細致的劃分。

流型辨識被當今學者主要分為兩種，一是對各級流型圖判定[4]，二是利用儀器儀表所測得的數據直接進行分析。

1ECT原理

電容層析成像[5-6]（electrical capacitance tomography，ECT）技術的測量原理是：多相流體的各相介質具有不同的介電常數，多相流混合體等價介電常數和電容值的測量變化是由各相組分濃度分布和變化引起的，電容值變化[7-8]會引起多相流介質相濃度大小和分布情況的改變。

電壓測量、電流激勵是ECT系統通常工作方式。場內的電導率發生變化不但改變場內電勢分布與電流場的分布，還會改變場域邊界上測量的電容值，邊界測量電容也包含了場域內電導率信息。先對水為滿管狀態下對應位置電壓進行測量，在對實際對象邊界電壓進行測量，利用相應計算機成像算法對兩組測量電壓值對比，便可重建出導電率分布情況，進行可視化測量。如圖1所示，電容層析成像系統主要由計算機圖像重建、電容傳感器陣列、數據采集系統三部分組成。

近年來對電容傳感器結構設計的研究成為了傳感器的研究熱點。對于傳感器陣列的分布信息可以從被測物場獲取。如果使用交流電壓電流刺激一下被測物，從被測物場的任意的角度我們都可以觀察出空間的敏感場。敏感陣列之所以能夠輸出相對應的信號是由于物場的內部不同電導率和敏感場的變化引起的。

電容極板之間的電容值可以看作為管道截面內所有點對該電容不同貢獻的疊加，因此，電極電容值就是來自管道截面內多相流體掃描，從管內多相流體任何一個方向或者角度投影所得到的數據就是實驗的電容值。電容層析成像的投影數據也就是電容值在多相流參數和圖像重建的各個階段中使用的數據。

通道的數據采集控制，A/D變換及通訊接口，電壓/電容（V/C）變換等組成電容數據采集系統，設計的重點和難點是電壓/電容（V/C）變換電路，電容層析成像越精確，系統的識別也就更加的精確。

對數據進行加工處理后，被測物場會有一個時間過程來形成二維或三維圖像，形成二維或三維圖像的時間過程就是計算機的圖像重建，過程設備或者裝置內部某個界面上的不同電導率分布可以直觀的顯示出來，可以使用相應知識的軟件庫，提取被測物場的內部信息：如流型、相含率、相速度、相尺寸等。成像系統控制外圍接口電路指令的發出，數據采集系統采集數據并接收數據，采用相應圖像重建算法對采集到的數據進行處理，以達到圖像重建效果。

2BP神經網絡

神經網絡是跨學科性非常強的一門學科，神經網絡[9-10]的應用與研究不但是計算機領域研究的熱點，其他學科領域的研究員如：醫用科學、人工智能研究、機械制造、生物研發等也開始研究神經網絡[11-12]。近二十幾年，神經網絡學術的研究也成為了學多學者研究的熱點，神經網絡在其他領域也得到了廣泛的應用。如模式識別、信號處理、聯想記憶、組合優化、自動控制、計算機視覺以及故障診斷等領域，這些領域的研究也都取得了比較高的成果。

多層前饋和多層的拓撲是BP神經網絡的結構特點，神經網絡的層數與復雜度成正比，包括輸入層、隱含層和輸出層，該層的神經元直接連接到下一層所有神經元，同層神經元不會出現連接的情況[13]。BP神經網絡結構如圖2所示。

BP神經網絡算法的實質可以簡單解釋，把樣本數據輸出與輸入問題變成一個非線性優化問題是，算法核心是基于極小化的二次函數，其原理是利用Delta學習的原理，當使用最速梯度下降方法時，權值開始沿著誤差函數負梯度方向變化，其流程如圖3所示。

BP神經網絡算法[14-15]的學習方法是典型的有導師訓練學習方法，許多學者雖然對BP神經網絡算法進行各種改進[16-17]，仍然不能達到理想的效果。雖然傳統BP神經網絡算法存在諸多缺點，本文只介紹3個經典的缺點：一是學習速度較慢，影響了整體的輸出結果。另外，BP神經網絡中的神經元、每一層閾值和權值不是一成不變的，而是隨著學習速度不斷進行改進和適應，全局逼近預測耗時過長，也能導致神經網絡整體收斂速度減慢；二是BP神經網絡算法易產生局部極小值，導致訓練失敗；三是BP神經網絡權值的初始化和層數的選取是隨機的，目前尚沒有正式理論的指導與參考。

以上3個缺陷嚴重影響BP神經網絡解決工業上復雜問題，為了使BP神經網絡解決復雜問題效率得到提高，本文針對前兩個缺陷做出一些適當改進。

3自適應學習與附加動量的BP神經網絡

傳統BP神經網絡算法是利用誤差對權值梯度下降進行不斷調節[18]，只要誤差不斷下降，我們就繼續調節，直到誤差不再改變為止。雖然提高網絡的收斂速度的方法有很多，但通過閱讀大量參考文獻，發現自適應學習方法明顯優于其它方法，故本文采用自適應學習方法來提高收斂速度，調節公式如下：

其中：c為本文最大誤差變化率，a、b、c的取值要憑著經驗獲得，取值為a=1.05，b=0.7，c=1.04。使用以上學習速率調節學習方法，學習速率得到了很大提高，但由于收斂速度過快而產生了一些振蕩，如圖4所示。

振蕩產生的原因為：傳統BP算法是一種簡單靜態尋優方法，如果需要改正 ω（k）時，可以在第κ步負梯度方向進行改正，考慮本次的測量值就夠了，因此會產生震蕩現象導致網絡收斂速度下降。為了提高收斂速度，本實驗是增加記錄上一次權值：實際權值的調整量是本次權值拿出一定的比例與上一次權值拿出一定的比例進行疊加，比例系數由經驗獲得。新算法的權值調節公式如下：

ω（κ+1）-ω（κ）=η（-Eω（κ））+mcω（κ）-ω（κ-1）（3）

其中：mc為動量因子。按照以上公式做，權值會在最小值收斂的方向減少振動，訓練時間必然減少。

圖5增加記錄上一次權值后產生的振蕩圖，與圖4相比，振蕩現象有了明顯減少。

此方法使用動量因子實際上增加了一個阻礙運動的一項因子，起到了減緩過度平滑的作用，在自適應學習速率的前提下附加動量，能夠減少了學習過程的振蕩趨勢，但不影響收斂速度的提高；對比如上兩圖不難發現，改進后不但可以減少誤差曲面局部細節的敏感性，而且還減少陷入局部極小值的可能性。

常量mc作為附加動量因子，當學習速率η發生變化，收斂速度和精度也會改變，動量項對減少誤差振蕩并沒有起到理想的效果。雖然傳統BP神經網絡算法存在很多缺陷，但是對于解決簡單工業問題，該方法也能夠達到理想效果；然而，我們實際工業問題大多數復雜多變的，由于問題的復雜性，誤差曲面是也極為復雜，會出現很多局部最小點，如果把調節的重點只關注動量因子調節，很難做到網絡誤差沿訓練的方向降低，振蕩現象也會因此產生。實驗在選取動量因子大小時應該憑借實驗經驗選取，因為動量因子是影響收斂效果的一個重要因素。當mc取值超過了一定值，學習速率η與網絡權值的調節量Δω也會因為mc得取值過大超出一定限度，網絡的訓練震蕩現象會很嚴重，誘發無法收斂的情況；如mc取值過于低，上次權重變化的方向也不會被完全記住，因此對本實驗沒有意義。

4仿真和驗證

120組樣本（每種20組樣本）中6種典型流型（滿管，層流，空管，環狀流，核心流，滴流）是典型的12電極ECT系統，我們使用Matlab7的環境進行訓練。每組電容的電容值都是確定的，240組試驗樣本（兩種算法對比共240組樣本）采取高斯噪聲法來確定，如下公式4作為具體確定輸入的節點，設Ng表示5dBm的高斯噪聲，神經網絡的四種不同輸入用

兩種神經網絡的輸出分成6個不同的流型，每一位6種不同流型用1×6的矩陣來代表，并設當矩陣元素其中一位為1時，其他元素為0時代表一種典型流型，如1，0，0，0，0，0T代表滿管，0，1，0，0，0，0T代表層流。1和0代表本實驗的輸出結果，兩種算法的六種流型中，輸出為1的為在其對應位置上，輸出為0的為在其他位置，由于條件有限我們所用實驗中噪聲的是不穩定，導致網絡輸出的1和0是也不能完全保證是正確的，為盡可能提高實驗輸出的準確性，對網絡訓練后的結果可以適當的增加一層競爭網絡函數處理，以達到增強神經網絡的抗干擾能力。由于去除噪聲干擾問題比較復雜，本文不做過多介紹。這樣做能避免輸出1和0的不確定性，這就是流型辨識[19-20]的效果。

經過大量實驗證明，隱含層節點的數量是9時，整體識別率曲線網絡的比例是最穩定的，隱含層節點數目太多或者太少都會影響實驗效果。多次試驗和歷史經驗可將0.01設置為學習率。本實驗采用梯度下降的自適應學習效率方法訓練函數（traingdx），采用非線性激活函數雙極S型激活函數（tansig）確定激活函數，函數的值域可用于區別雙極S形函數與S形函數（logsig），S形函數值域設為（0，1），雙極S形函數的值域設置為（-1，1），以上數據的設置是憑借實驗經驗設置的，能夠提高實驗效率。

由于神經網絡權值的初始值是任意的，從而導致網絡不穩定[21]。為了驗證自適應學習方法能夠提高流型辨識的識別率，為了簡化實驗的復雜度，迭代次數不超過500，對傳統BP神經網絡和具有自適應學習的BP神經網絡（ABP）進行ECT流型辨識，表1為實驗后的結果。

對表1進行分析與總結，實驗結果證明了具有ABP算法在對幾種典型的流型的識別率得到了提高，但是對于一些工業的發展這樣的流型識別率還是不夠的。因此本文提出了傳統BP神經網絡算法不但具有自適應學習能力還有附加動量功能。

由于神經網絡的實驗訓練存在誤差，本實驗將0.01設置為本次實驗訓練的目標誤差，在試驗過程中神經網絡的迭代次數是不可預知的，憑借實驗經驗，在簡化實驗復雜度但不影響實驗效果的情況下，5000次迭代次數作為上限，圖6就是我們經過實驗驗證后的兩種神經網絡訓練曲線。

圖6可以得出結論，改進后BP神經網絡算法不但訓練曲線比傳統BP神經網絡平滑，而且訓練次數也明顯減少，改進BP神經網絡只要93次就可以達到目標，而傳統BP神經網絡訓練的迭代次數要124次，才能達到目標。另一方面，BP神經網絡的初始值選取對訓練結果有較大的影響，初值選取不一樣導致每次訓練結果不可能相同，初始值選取不同對改進BP神經網絡實驗結果影響不大，可以忽略不計。表2是兩種算法進行實驗后得到的識別率。

表2對工業上ECT中幾種常見的流型都做了實驗，根據ECT流型辨識后結果進行分析與比較，顯而易見的是改進后BP神經網絡的識別率提高了很多，值得一提的是中位流和滿管使用改進后BP神經網絡算法進行流型辨識實驗，結果發現辨識率達到了100%，無論在科研還是在實際工業的發展都有積極的作用。

5結論

在解決ECT流型辨識的問題上，本文根據傳統BP神經網絡存在的缺陷，進行了改進，首先使傳統BP神經網絡算法具有自適應學習能力，進行對比實驗，發現識別率提高了，但沒有達到預期效果，又在自適應學習基礎上提出了附加動量，即本文所說的改進BP神經網絡算法，并把改進后的BP神經網絡與傳統BP神經網絡的分別進行ECT系統流型辨識實驗，并對實驗結果進行分析與對比，發現本文改進后的算法不但能使ECT系統流型辨識的準確率得到提高，還較少了ECT流型辨識的迭代次數，收斂速度和性能也有了明顯的提高；此方法不但為在ECT系統流型辨識方法研究提供一個很好思路和方法，又對工業的發展起到了積極作用。

參 考 文 獻：

[1]楊道業，施源，徐鋅鋒.基于雙截面ECT的氣/固兩相流參數檢測系統[J].儀器儀表學報，2013，34（9）：1968-1969.

[2]陳德運，高明，宋蕾，等.一種新型的三維ECT傳感器及三維圖像重建方法[J].儀器儀表學報，2014（5）：961-968.

[3]CHEN Deyun，WANG Lili，CHEN Yu.Analyses and Simulation of Sensor Structure Parameters for Electrical Capacitance Tomography System [J].Proceedings of SPIE（The International Society for Optical Engineering），2008，66（21）：575-578.

[4]陳德運，張華，朱波，等.油水兩相流電阻層析成像系統流型的辨識[J].電機與控制學報，2007（6）：639-643.

[5]田海軍，周云龍.電容層析成像技術研究進展[J]. 化工自動化及儀表，2012（11）：1387-1392.

[6]高彥麗，章勇高，聶水果，等.高速電容層析成像系統的硬件關鍵技術研究[J]. 電測與儀表，2010（2）：13-16.

[7]吳新杰，黃國興，王靜文.壓縮感知在電容層析成像流型辨識中的應用[J].光學精密工程，2013（4）：1062-1068.

[8]宋蕾，陳德運，姚玉梅，等.Elman神經網絡在ECT系統流型辨識中的應用[J].哈爾濱理工大學學報，2014，19（5）：103-108.

[9]宋志杰，王健.模糊聚類和LM算法改進BP神經網絡的變壓器故障診斷[J].高壓電器，2013（5）：54-59.

[10]林虹江，周步祥，冉伊，等.基于遺傳優化BP神經網絡算法的光伏系統最大功率點跟蹤研究[J].電測與儀表，2015（5）：35-40.

[11]師洪濤，楊靜玲，丁茂生，等.基于小波-BP神經網絡的短期風電功率預測方法[J].電力系統自動化，2011（16）：44-48.

[12]李松，劉力軍，解永樂.遺傳算法優化BP神經網絡的短時交通流混沌預測[J].控制與決策，2011（10）：1581-1585.

[13]夏玫.BP神經網絡泛化能力改進研究[D].太原：太原科技大學，2009：24-26.

[14]徐黎明，王清，陳劍平，等.基于BP神經網絡的泥石流平均流速預測[J].吉林大學學報（地球科學版），2013（1）：186-191.

[15]李波，柳華橋，戴鑫，等.標準BP神經網絡算法和附加動量法在沉降監測中的應用研究[J].城市勘測，2016（1）：145-148.

[16]王樹森，趙冬玲.一種基于附加動量法的改進BP算法[J].濟源職業技術學院學報，2012（3）：9-13.

[17]王燕妮，樊養余.改進BP神經網絡的自適應預測算法[J].計算機工程與應用，2010（17）：23-26.

[18]尹光志，李銘輝，李文璞，等.基于改進BP神經網絡的煤體瓦斯滲透率預測模型[J].煤炭學報，2013（7）：1179-1184.

[19]陳德運，朱波，張華.基于小波包分析和RBF神經網絡的ERT系統流型辨識[J].計算機工程與應用，2008（6）：231-233.

[20]劉延東，李惠強，何在剛，等.基于粗神經網絡和特征提取的ECT流型辨識[J].遼寧大學學報：自然科學版，2014（4）：330-337.

[21]冀海峰，黃志堯，王保良，等.基于信息融合技術的氣固流化床流型辨識[J].儀器儀表學報，2002（S2）：897-899.

（編輯：溫澤宇）