確定延時爆破間隔時間的新方法

張小軍 汪旭光 于亞倫 楊德強(qiáng)

(1.北京科技大學(xué)土木與資源工程學(xué)院，北京 100083；2.北京礦冶研究總院，北京 100160)

隨著城市的發(fā)展，現(xiàn)有的城市空間尤為不足，人們開始進(jìn)行城市改造和向地下空間探索。但是城市拆除工程環(huán)境復(fù)雜、城市隧道埋深比較淺，并且毗鄰建筑物和各類地下管線，所以對爆破振動控制的要求非常苛刻。目前工程中常用的減振技術(shù)有分散裝藥、延時爆破、預(yù)裂爆破、減小斷面或進(jìn)尺等，甚至采用靜態(tài)破碎的方法等，以保證爆破施工的順利進(jìn)行[1-2]。

延時爆破是目前應(yīng)用最廣泛的減振手段之一。

廖先葵等在礦山大規(guī)模爆破中，采用對稱分區(qū)，延時爆破等方法，實現(xiàn)了爆破地震波干擾減振的目的[3]；田振農(nóng)等通過時頻分析方法對隧道爆破振動的一般特征進(jìn)行了分析，結(jié)果表明爆破地震波是多列爆炸波疊加的結(jié)果[11]；傅洪賢等結(jié)合蘭渝鐵路的建設(shè)，在人和場隧道進(jìn)行電子雷管降振試驗、電子雷管與非電雷管聯(lián)合降振試驗，得出隧道電子雷管單孔連續(xù)起爆降振技術(shù)，與隧道非電雷管爆破相比，爆破振動降低80%以上[8]；根據(jù)Basebi等的工程試驗研究[10]，采用單孔單響的電子雷管起爆，爆破振動可以降低約三分之一；高文學(xué)等結(jié)合基礎(chǔ)開挖工程，探討了電子雷管起爆技術(shù)及其在復(fù)雜環(huán)境下深孔爆破工程的應(yīng)用，研究表明電子雷管可以精確且合理地延時時間，可以達(dá)到良好的降振效果，結(jié)合預(yù)裂控制爆破，降振效果更加顯著[12]。上述研究基本都證明了延時爆破可以達(dá)到減振的目的，并且效果顯著，但是都沒有明確提出確定延時爆破間隔時間的方法。

本研究主要依據(jù)波的疊加原理和波的干涉，對爆破地震波的疊加效應(yīng)進(jìn)行了理論分析，得出延時爆破的最佳間隔時間。同時以理論分析為基礎(chǔ)，利用波形峰值包絡(luò)線的思想與爆破地震波疊加的波動方程，推導(dǎo)出了爆破地震波疊加的簡析式。最后通過案例，利用單炮次爆破振動波形圖，摘取其峰值數(shù)據(jù)，擬合出了測點處質(zhì)點振動速度的表達(dá)式，根據(jù)不同延時間隔時間爆破振動的理論波形圖，確定出最佳的延時爆破間隔時間。

1 爆破地震波的疊加規(guī)律

爆破地震波的傳播是極為復(fù)雜的，質(zhì)點振動強(qiáng)度的衰減規(guī)律受到諸多因素的影響。在延時爆破中，某質(zhì)點的振動受到若干炮孔炸藥爆炸的影響。為了實現(xiàn)減振的目的，需要對雷管的延時間隔時間進(jìn)行確定。以下是通過建立模型，理論計算雷管的精確延時間隔時間。

設(shè)相鄰的2個炮孔A和炮孔B距測點C的距離近似相等，爆破引起的振動近似為簡諧振動。炮孔和測點示意圖如圖1所示。

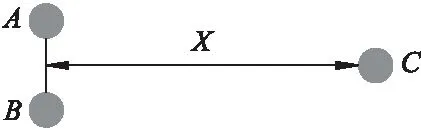
圖1 炮孔與測點

圖1中，A、B為相鄰的2個炮孔，C為振動測點；A、B到C點的距離近似相等，為X。

由炮孔A爆炸產(chǎn)生的振動波形圖如圖2。其波動方程為

y=asinwt,

(1)

式中，a為振幅；W為圓頻率；t為時間；y為A點處質(zhì)點在時刻t離開其平衡位置的位移。

圖2 炮孔A爆炸產(chǎn)生的振動波形

由于振動是從A點到C點傳播的，所以C點處質(zhì)點的振動落后于A點，其落后時間為X/c，c指波的傳播速度，所以C點在時刻t的位移等于A點處質(zhì)點在時刻(t-X/c)的位移。所以C點處質(zhì)點振動的波動方程為

(2)

因為

(3)

cy=λ,

(4)

式中，f為頻率；λ為波長；T為周期。

即

(5)

為了實現(xiàn)炮孔A和炮孔B是延時爆破，設(shè)炮孔B延時Δt爆炸，其波動方程為

y=asinw(t-Δt).

(6)

由于振動是從炮孔B到測點C傳播的，所以C點處質(zhì)點的振動落后于B點,其落后時間為X/c，所以C點在時刻t的位移等于B點質(zhì)點在時刻(t-X/c)的位移，所以C點處質(zhì)點振動的波動方程為

(7)

根據(jù)式(3)、式(4)，式(7)變換為

(8)

爆破地震波是由不同頻率、不同幅值的波在一個有限時間范圍內(nèi)組合的隨機(jī)過程。地震波的最大幅值、頻率和持續(xù)時間被稱為地震波的3要素。而最大振幅又與速度、加速度密切相關(guān)，故地震波的速度、頻率和持續(xù)時間是表征地震波強(qiáng)度的3個必不可少的參量，其中振速是最常用的，那么式(5)對時間t進(jìn)行求導(dǎo),即為A炮孔爆炸C處質(zhì)點振動速度：

(9)

式(8)對時間t進(jìn)行求導(dǎo),即為B炮孔爆炸C處質(zhì)點振動速度：

(10)

炮孔A和炮孔B的振動傳播到測點C時，C點的振動就是2列振動波的疊加，那么測點C處質(zhì)點振動的合速度為

vc=vac+vbc=

(11)

根據(jù)振動的合成公式，式(11)合成為

(12)

其中，

(13)

(14)

從式(11)、式(13)中可以發(fā)現(xiàn)，這2列波在空間任一點的位相差為

Δφ=2πcΔt/λ,

(15)

而Δφ的取值影響測點C振動合成式(13)中振速峰值b的大小。所以當(dāng)：

(16)

根據(jù)式(13)，測點C處質(zhì)點的振動速度峰值最大。

當(dāng)：

(17)

根據(jù)式(13)，測點C處質(zhì)點的振動速度峰值最小，那么延時爆破的最佳間隔時間為

k=0,1,2,…

(18)

式中，T為質(zhì)點振動周期。

所以延時爆破的最佳間隔時間，即半個周期或半個周期的奇數(shù)倍。

2 振速包絡(luò)線以及合成振速近似簡析式

事實上，爆破振動并不是簡單的簡諧振動，質(zhì)點在振動過程中總會受到一些阻力，振動的能量要不斷轉(zhuǎn)化為其他形式的能量。根據(jù)振動物體的動能公式式(19)，振動物體的動能跟振速的平方成正比，動能隨時間減少，振速也隨時間減小，如果不給予能量補(bǔ)充，那么經(jīng)過一段時間后，振動就要停止，如圖3所示。

(19)

式中，Ek為振動物體動能；m為質(zhì)量；v為物體振動速度。

為了更好地描述爆破振動的特性，引入爆破振動速度波形峰值包絡(luò)線的概念，通過爆破振動速度波形峰值包絡(luò)線的簡析式與第1節(jié)中依據(jù)爆破地震波疊加理論推導(dǎo)的公式相結(jié)合，得出測點處質(zhì)點振動速度的近似解析式。

2.1 振速包絡(luò)線

不管在爆破振動的監(jiān)測過程中還是對爆破振動效應(yīng)的預(yù)防中，往往比較關(guān)心的是爆破振動的峰值速度。那么通過對爆破振動速度波形峰值摘取，然后對這些摘取的數(shù)據(jù)進(jìn)行擬合，即可得到光滑的爆炸地震波波形峰值包絡(luò)線，如圖3所示。

圖3 爆破振動速度

從圖3中以及其他的爆破振動速度波形圖中，可以得到爆破振動波形峰值包絡(luò)線的近似解析式，其形式如下：

V=k′e-βt,

(20)

式中，V為介質(zhì)質(zhì)點振動速度峰值，cm/s；k′為與炮孔炸藥量、爆心距等有關(guān)的系數(shù)；β為與爆破場地環(huán)境有關(guān)的指數(shù)；t為時間，s。

其中k′跟炮孔的裝藥量、測點距爆源的距離、爆破場地環(huán)境等有關(guān)系，可以近似看作：

(21)

則式(20)變換為

(22)

2.2 合成振速近似解析式

為了研究爆破振動的質(zhì)點振動速度，需要知道質(zhì)點振動速度的簡析式，根據(jù)第1節(jié)的理論推導(dǎo)，將式(9)作變量代換，令：

(23)

則式(9)變換為

(24)

同理將式(10)作變量代換，令：

(25)

則式(10)變換為

(26)

所以式(25)、式(26)合成為

(27)

即：

(28)

式中，

(29)

根據(jù)式(22)則：

(30)

(31)

(32)

根據(jù)實際情況，測點處的質(zhì)點振動要歷經(jīng)3個階段，第1個階段是傳播階段，即從炮孔爆炸到爆破振動傳遞到測點處，需要一定的時間，在這個階段測點處的質(zhì)點振動速度為零；第2個階段是單振動階段，即最先傳遞到測點處的爆破振動引起測點處質(zhì)點振動；第3個階段是雙振動階段，即2炮孔爆炸引起的振動都傳遞到測點處引起測點處質(zhì)點振動,并且各個階段之間的振動波形曲線會不連續(xù)，會發(fā)生跳躍。所以測點處質(zhì)點振動速度的表達(dá)式為

(33)

3 案 例

3.1 工程概況

某居住小區(qū)Ⅱ標(biāo)土石方爆破工程東面緊鄰公路，西面160 m為一些土窯洞，這些土窯洞將要作為歷史文物，需要保護(hù)。北面為已開挖完成的施工場地，南面為山體。周邊環(huán)境如圖4所示。為了防止爆破對土窯洞造成影響，爆破工程采取延時爆破減振措施。

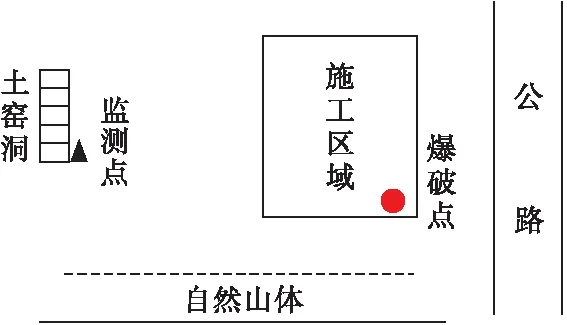
圖4 周邊環(huán)境

3.2 數(shù)據(jù)擬合

為了確定延時爆破間隔時間，首先進(jìn)行單炮次試爆，根據(jù)單炮次的爆破振動速度波形圖，進(jìn)行數(shù)據(jù)擬合。單炮次藥量15 kg，試爆地點選在施工區(qū)域爆破點附近，監(jiān)測點距離160 m。其測點處質(zhì)點振動速度波形見圖5。

根據(jù)單炮次爆破振動速度波形圖，選取圖中峰值的8個點，見圖5中的標(biāo)記，將其整理到表1。

根據(jù)表1中的8組數(shù)據(jù)，按照式(22)進(jìn)行非線性曲線擬合，得到單炮次爆破振動速度峰值包絡(luò)線，見圖6。

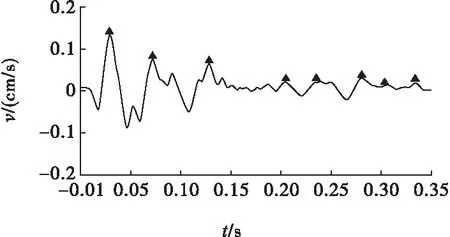
圖5 單炮次爆破振動波形

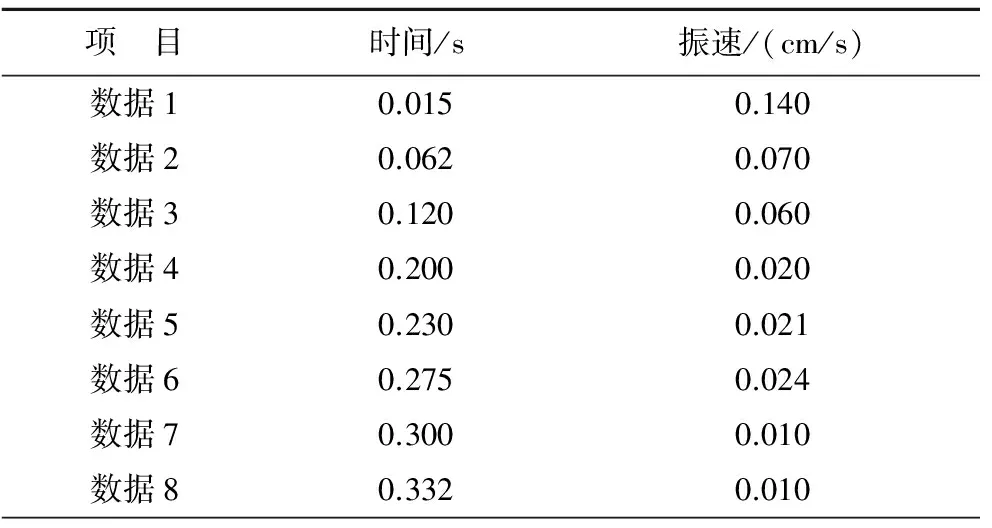
項 目時間/s振速/(cm/s)數(shù)據(jù)10．0150．140數(shù)據(jù)20．0620．070數(shù)據(jù)30．1200．060數(shù)據(jù)40．2000．020數(shù)據(jù)50．2300．021數(shù)據(jù)60．2750．024數(shù)據(jù)70．3000．010數(shù)據(jù)80．3320．010

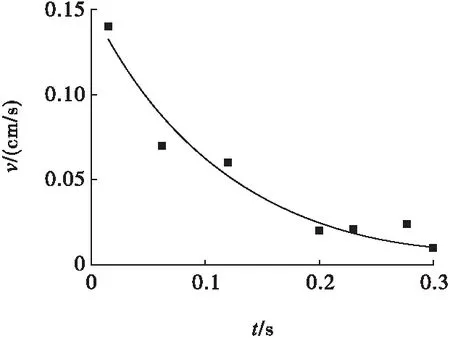
圖6 單炮次爆破振動速度峰值包絡(luò)線

其擬合公式為

(34)

3.3 不同延時間隔時間測點處質(zhì)點的振動速度

根據(jù)段如泰在《用地震定位方法研究礦山爆破中的地震波傳播速度》一文中的敘述，爆破地震波的傳播速度為v=4 498.85 m/s(或王進(jìn)強(qiáng)在《地震波傳播速度原位試驗及計算》一文中敘述爆破地震波的平均傳播速度為4 810 m/s)，其地質(zhì)條件與該爆破工程類似，所以在該工程中爆破地震波的傳播速度取 4 498.85 m/s[14]；爆破地震頻率在10～100 Hz，這里取頻率25 Hz，周期為0.04 s，波長為179.95 m。不同炮孔距測點的距離看作近似相等。現(xiàn)對不同延時間隔時間的2炮孔爆炸引起測點處質(zhì)點振動速度進(jìn)行討論，每個炮孔取藥量為15 kg。

(1)Δt=0 s。根據(jù)式(29)、式(32)得：

A=2×0.135 8e-7.932(t-0.035 5),

(35)

tanφ=0.842 6,φ=0.699,

(36)

則測點處質(zhì)點振動速度方程為

(37)

測點處質(zhì)點振動速度波形圖見圖7所示。

圖7 Δt=0 s測點處質(zhì)點振動速度波形

(2)Δt=0.02 s。根據(jù)式(29)、式(32)得：

A=0.030 9e-7.932t

(38)

tanφ=0.859 0,φ=0.709 7

(39)

則測點處質(zhì)點振動速度方程為

(40)

測點處質(zhì)點振動速度波形圖見圖8所示。

圖8 Δt=0.02 s質(zhì)點振動速度波形

(3)Δt=0.025 s。根據(jù)式(29)、式(32)得

A=0.156 8e-7.932t，

(41)

tanφ=-1.658 5,φ=-1.028 2，

(42)

則測點處質(zhì)點振動速度方程為

(43)

測點處質(zhì)點振動速度波形圖見圖9所示。

圖9 Δt=0.025 s質(zhì)點振動速度波形

(4)Δt=0.05 s。根據(jù)式(29)、式(32)得：

A=0.323 0e-7.932t，

(44)

tanφ=-0.283 849,φ=-0.276 6，

(45)

則測點處質(zhì)點振動速度方程為

(46)

測點處質(zhì)點振動速度波形圖見圖10所示。

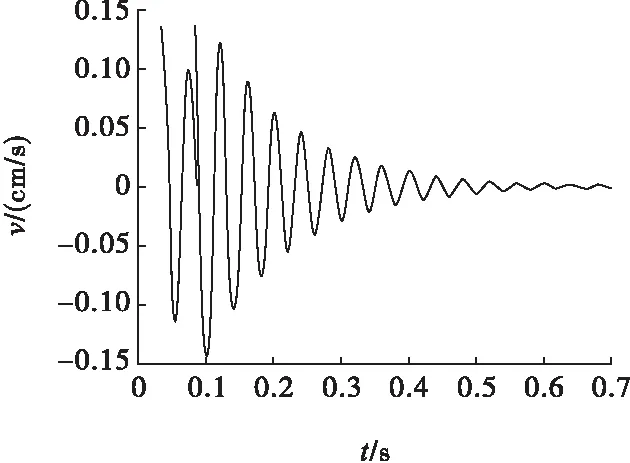
圖10 Δt=0.05 s 質(zhì)點振動速度波形

從圖7、圖8、圖9、圖10中可以看出炮孔爆炸的瞬間，測點處的質(zhì)點振動速度為零，也就是地震波還沒有傳播到測點處，其傳播需要一定的時間；圖7中測點處質(zhì)點振動速度峰值最大。圖8中測點處質(zhì)點振動速度峰值最小，但是剛開始的時候還是比較大的，不可忽視。

根據(jù)圖8，測點處質(zhì)點振動速度峰值最小，那么該爆破工程選擇延時間隔時間為0.02 s的雷管是最佳的，但是現(xiàn)場選用的是奧瑞凱高精度導(dǎo)爆管雷管，其段別有限，只有延時25 ms、50 ms等的雷管供選用，那么通過比較圖9和圖10，間隔0.025 s的振速峰值要比間隔0.05 s的振速峰值小，同時圖10中可以看出會出現(xiàn)反復(fù)的情況，即振速將低后有驟升的現(xiàn)象，所以該爆破工程建議選用延時間隔時間為25 ms的高精度導(dǎo)爆管雷管來實施爆破。

3.4 現(xiàn)場爆破

根據(jù)上述的理論分析，實際單孔裝藥量15 kg，最大段藥量15 kg，總裝藥量420 kg，孔內(nèi)500 ms高精度導(dǎo)爆管雷管，孔間25 ms的高精度導(dǎo)爆管雷管實施爆破，在測點處監(jiān)測到的波形圖如圖11所示。

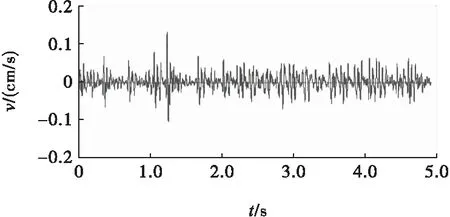
圖11 測點處爆破振動速度波形

從圖11可以看出選用延時間隔25 ms的高精度雷管，測點處質(zhì)點的振速大部分都在0.1 cm/s之內(nèi)，只有個別超出0.1 cm/s，但小于0.15 cm/s，與圖9的波形圖相吻合，基本沒有對窯洞以及其他設(shè)施造成破壞，爆破取得了成功。

4 結(jié) 論

(1)通過建立數(shù)學(xué)模型、理論分析，得出了延時爆破的最佳間隔時間，即半個周期或半個周期的奇數(shù)倍。

(2)利用單炮次的爆破試驗，推導(dǎo)出了2孔延時爆破振動速度的理論簡析式，從而可以畫出測點處質(zhì)點振動的速度波形圖，使研究問題更加形象化。

(3)2孔延時爆破測點處的質(zhì)點振動要歷經(jīng)3個階段，分別是傳播階段、單振動階段、雙振動階段。

(4)根據(jù)測點處質(zhì)點振動速度表達(dá)式畫出的理論波形圖，可以確定最佳的延時爆破間隔時間。如果現(xiàn)有爆破器材實現(xiàn)不了最佳間隔時間，可以根據(jù)理論波形圖，選擇較優(yōu)的延時爆破間隔時間。

(5)本研究對延時爆破間隔時間的確定提供了新的思路與方法。

[1] 孫冰峰,傅洪賢,管曉明，等.基于建筑物模態(tài)分析的隧道爆破減振技術(shù)[J].中國公路學(xué)報,2016,29(10):86-94.

Sun Bingfeng,Fu Hongxian,Guan Xiaoming,et al.Decreasing vibration technology for tunnel blasting based on building modal analysis[J].China Journal of Highway and Transport,2016,29(10):86-94.

[2] 李鎮(zhèn)明,張 瑀,周廣春.單自由度體系有阻尼自由振動振幅包絡(luò)線的性質(zhì)研究與數(shù)學(xué)證明[J].數(shù)學(xué)的實踐與認(rèn)識，2015,45(21):227-232.

Li Zhenming,Zhang Yu,Zhou Guangchun.Characteristics of the envelope of damped free vibrations of SDOF systems and its proof[J].Mathematics in Practice and Theory,2015,45(21):227-232.

[3] 廖先葵.深孔爆破大規(guī)模干擾減震機(jī)理及其應(yīng)用[J].爆 破,1993(4):1-6.

Liao Xiankui.Large scale interference shock absorption mechanism and its application in deep hole blasting[J].Blasting,1993(4):1-6.

[4] 劉清泉,李玉民.城市地下工程的減震爆破技術(shù)[J].煤炭科學(xué)技術(shù),1991(10):13-15.

Liu Qingquan,Li Yumin.Cushion blasting technique for city underground project[J].Coal Science and Technology,1991(10):13-15.

[5] 薛孔寬,唐光榮,曹恒安，等.分段微差爆破地震效應(yīng)的疊加分析[J].爆破,1991(3):67-71.

Xue Likuan,Tang Guangrong,Cao Heng′an,et al.Overlapping analysis of seismic effects of particle borehole blasting[J].Blasting,1991(3):67-71.

[6] 魏曉林,劉 翼.爆破拆除樓房時塌落振動的預(yù)測[J].工程爆破,2016,22(2):13-18.

Wei Xiaolin,Liu Yi.Prediction of collapse vibration of building demolished by blasting[J].Engineering Blasting,2016,22(2):13-18.

[7] 張 迪.地鐵隧道精確延時爆破振動傳播規(guī)律與控制試驗研究[D].北京:中國礦業(yè)大學(xué)(北京),2016.

Zhang Di.Vibration Propagation Regularity and Control Experiment Research of Metro Tunnel with Precise Delay[D].Beijing:China University of Mining and Technology (Beijing),2016.

[8] 陳繼強(qiáng),劉為洲.多孔爆破振動強(qiáng)度的單孔波形疊加計算[J].金屬礦山,2000(8):23-25.

Chen Jiqiang,Liu Weizhou.Single hole waveform superimposed calculation of the vibration strength of multihole blasting[J].Metal Mine,2000(8):23-25.

[9] 陳士海,燕永峰,戚桂峰，等.微差爆破將震效果影響因素分析[J].巖土力學(xué),2011,32(10):303-308.

Chen Shihai,Yan Yongfeng,Qi Guifeng,et al.Analysis of influence factors of interence vibration reduction of millisecond blasting[J].Rock and Soil Mechanics,2011,32(10):303-308.

[10] Basebi T,Thomas R M.A study of moving mesh methods applied to a thin flame propagating in a detonator delay element[J].Computers and Mathematics with Applications,2003,45(1):131-163.

[11] 田振農(nóng),孟祥棟,王國欣.城區(qū)隧道電子雷管起爆錯相減震機(jī)理分析[J].振動與沖擊,2012,31(21):108-111.

Tian Zhennong,Meng Xiangdong,Wang Guoxin.Mechanism analysis of fault-phase vibration reduction for tunnel blasting initiated by electronic detonators in city area[J].Journal of Vibration and Shock,2012,31(21):108-111.

[12] 胡建華,尚俊龍,羅先偉,等.單孔爆破振動監(jiān)測與衰減規(guī)律多元線性化回歸[J].振動與沖擊,2013,32(16):49-53.

Hu Jianhua,Shang Junlong,Luo Xianwei,et al.Monitoring of single-hole blasting vibration and detection of its attenuation law by using multiple linear regression[J].Journal of Vibration and Shock,2013,32(16):49-53.

[13] 喻 軍,劉松玉,童立元.淺埋隧道爆破振動空洞效應(yīng)[J].東南大學(xué)學(xué)報:自然科學(xué)版,2010,40(1):176-179.

Yu Jun,Liu Songyu,Tong Liyuan.Hollow effect induced by blasting vibration in shallow tunnels[J].Journal of Southeast University:Natural Science Edition,2010,40(1):176-179.

[14] 段如泰,金振奎,索重輝,等.用地震定位方法研究礦山爆破中的地震波傳播速度[J].科學(xué)技術(shù)與工程，2011,11(36):8967-8977.

Duan Rutai,Jin Zhenkui,Suo Chonghui,et al.Earthquake location method used in velocity study of mine explosion stimulating seismic wave[J].Science Technology and Engineering,2011,11(36):8967-8977.

[15] 胡鶴飛.MATLAB及應(yīng)用[M].北京:北京郵電大學(xué)出版社,2012.

Hu Hefei.MATLAB and Its Application[M]:Beijing University of Posts and Telecommunications Press,2012.

[16] 李洪濤,盧文波,舒大強(qiáng),等.爆破地震波的能量衰減規(guī)律研究[J].巖石力學(xué)與工程學(xué)報,2010,29(1):3364- 3369.

Li Hongtao,Lu Wenbo,Shu Daqiang,et al.Study of energy attenuation law of blast-induced seismic wave[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(1):3364-3369.

[17] 龔 敏,趙振振,吳昊駿,等.針對建構(gòu)筑物不同振速要求的隧道爆破藥量計算方法[J].煤炭學(xué)報,2016,41(7):1747-1753.

Gong Min,Zhao Zhenzhen,Wu Haojun,et al.Computational method of blasting charges under different vibration velocity limits of buildings and structures around tunnel[J].Journal of China Coal Society,2016,41(7):1747-1753.