RBF神經網絡補償的并聯機器人控制研究

彭志文，高宏力，梁 超，文 剛

（西南交通大學 機械工程學院，四川 成都 610031）

1 引言

三自由度Delta機器人是食品、藥品分揀包裝等生產線上的關鍵組成部分[1]，由于機構三個運動支鏈對稱安裝使其有著剛度大、無累積誤差等優勢。在系統的控制方面，機構的并聯特性使其成為一個高度耦合的非線性系統。針對系統的解耦控制，基于動力學模型的控制算法跟蹤效果優于傳統的運動學控制。目前，被廣泛應用的是計算力矩控制策略[2]。在系統動力學模型可以準確推導的前提下，計算力矩法可以實現對理想軌跡準確的跟蹤[3]。在實際運用中，由于存在很多干擾和不確定性，只能推導出理想情況下的系統動力學模型，而不能獲得被控對象的真實模型[4]。針對并聯機器人的模型強耦合性和不確定性，文獻[5]提出了一種模糊PD控制策略，詳細的分析了系統噪聲來源。針對Delta機器人，提出一種計算力矩法基礎上的RBF神經網絡在線補償控制策略。RBF神經網絡結構簡單，運算量小，泛化能力較強，可以很好的應用于要求實時性的機器人運動控制。在RBF神經網絡中，無需進行離線訓練，實時運行中以關節角度誤差及其變化率作為網絡輸入，得到力矩補償值和計算力矩的輸出共同控制系統實現對目標軌跡準確跟蹤。

2 計算力矩控制策略

針對三自由度Delta機器人，基于虛功原理法建立機構動力學方程。與其他工業機器人相似，Delta機器人動力學方程也能夠表示為如下形式

式中：M（α）—質量慣性矩陣；C（α，α˙）—柯氏力和向心力矩陣；

N（α）—重力矩陣；α—驅動臂轉動角度向量；τ—驅動臂驅

動力矩；τ—外部擾動。

由式（1）可以看出系統具有很強的非線性和耦合性。一般的基于動力學設計的計算力矩控制策略如下：

式中：M^（α）—質量矩陣分項的估計；C^（α，α˙）α˙—科氏力、向心力分項的估計；N^（α）—重力分項的估計；e—關節位置誤差；e˙—關節速度誤差；Kp，Kd—控制參數矩陣。

在理想情況下，即假設動力學建模準確，系統名義模型與實際模型一致且無外部擾動。有M^（α）=M（α），C^（α，α˙）=C（α，α˙），N^（α）=N（α）。將式（2）代入式（1）可得系統閉環誤差方程為e¨+Kpe+Kde˙=0 。在實際應用中，幾乎不可能得到完整真實的模型，存在各種確定和不確定的外部擾動。那么名義模型與系統真實模型之間存在偏差ΔM=M-M^，ΔC=C-C^，ΔN=N-N^。因此在實際情況下，系統閉環誤差方程為

由式（3）可知，用普通的計算力矩控策略無法使誤差收斂到0。

3 RBF神經網絡補償控制策略

3.1 RBF神經網絡結構

RBF網絡結構簡單，是一個單隱層前饋網絡，具有很強的泛化能力。RBF網絡已經被證明能夠以任何精度逼近任何非線性函數[6-7]。不妨設 X=［x］T為網絡輸入，隱層是徑向基函數 H=［h］T，

ij為高斯基函數，表示隱層第j個神經元的輸出。Cj=［cj1，cj2，…cjm］為RBF網絡節點j的高斯基函數中心。b=［b1，b2，…bm］，bj為節點 j高斯基函數寬度。θ=［θ1，θ2，…θm］為網絡權值向量，網絡的輸出為 y（t）=θTh=θ1h1+θ2h2+…+θmhm。

3.2 系統RBF神經網絡補償

針對普通的計算力矩控制策略無法實現準確跟蹤問題，作出對系統建模誤差進行補償的研究，提出基于在線學習的RBF神經網絡補償的控制策略。計算力矩策略作為主體，保證系統的穩定性，同時RBF網絡在線學習優化權值，不斷逼近模型不確定性。控制系統的框圖，如圖1所示。

圖1 控制系統框圖Fig．1 The Control System Diagram

設計的網絡輸入層為三個驅動關節的角度誤差及其導數，包含6個神經元；隱層包含5個節點；輸出層為三個驅動臂的轉矩補償值。根據式（3），不確定性會影響控制精度，需要RBF網絡在線自適應逼近系統的不確定性 f=M^-1（ΔMα¨+ΔCα˙+ΔN-τ），從

d而實現對系統不確定性的在線補償。在線補償過程中，RBF網絡在機器人末端軌跡實時跟蹤過程中被訓練，根據軌跡位置和速度誤差在線修正網絡權值，不斷逼近最佳輸出，避免了RBF網絡的離線訓練過程。令fi表示RBF網絡的最佳輸出，θi表示對f最佳辨識的網絡權值，則fi=θTih。令fe表示網絡的實際輸出，θe表示實際網絡權值，則f=θTh。由文獻[8]可知，網絡的建模誤差有界，其上

ee加入RBF網絡在線補償的控制律為：

不妨令 τ1＝M^（α）（α¨d+Kpe+Kde˙）+C^（α，α˙）α˙+N^（α），τ2=M（α）fe，則 τ＝τ1+τ2。τ1表示計算力矩控制部分，τ2表示 RBF 網絡不確定性補償部分。將RBF網絡在線補償控制律代入式（1）整理得：

3.3 系統穩定性分析及權值自適應律推導

令 x=［e，e˙］T，那么可以將式（5）轉化為

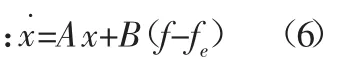
4 聯合仿真與結果分析

驗證RBF網絡在線補償控制策略的準確性，對比不同策略下的控制效果。對Delta并聯機器人進行Simulink/Simmechanics聯合仿真分析。在Simulink中設計系統控制器，在Simmechanics中建立機構虛擬物理模型，把Simmechanics虛擬樣機作為控制對象，通過接收驅動力矩和反饋旋轉速度、加速度，進行數據交互，完成系統聯合仿真。

4.1 聯合仿真模型建立

Simmechanics是Matlab中根據物理結構進行建模的插件[10]，在Simmechanics中進行機器人模型的建立。模塊化和圖形化的建模方式使得模型結構簡潔，同時在Matlab主界面可以直接觀察機構的運動畫面，實時了解軌跡跟蹤效果，有利于控制器的改進，是一種快捷且高效的輔助動力學分析方法。Delta機器人的物理模型，如圖2所示。

圖2 Delta機器人Simmechanics模型Fig．2 The Simmechanics Model of Delta Robot

Simmechanics中的Delta并聯機器人虛擬樣機是一個四面體結構，有三條相同的對稱布置支鏈。由于其支鏈的平行四邊形結構，Delta機器人只能在一定空間范圍內平動。定義機器人各鉸鏈之間的約束關系，使其真實的模擬機構的運動狀態。根據控制策略，在Simulink中建立系統控制器，輸出驅動力矩信號，驅動機器人末端動平臺跟蹤期望軌跡，Simmechanics實時檢測并反饋機器人的速度和加速度信息到系統控制器，實現聯合仿真。

4.2 結果與分析

選擇末端動平臺的跟蹤軌跡為半徑50mm的圓，Z方向保持高度恒定。選取平臺初始位置為（0.01，0.04，0.82），三個驅動臂初始角速度為0。Delta機器人系統動力學模型如式（2），具體表述如下：

式中：E—單位矩陣；J—速度雅克比矩陣。M（α），C（α，α˙），N（α）—質量矩陣分項、向心力分項和重力分項。

在仿真模型中，選取機器人的結構參數，如表1所示。

表1 Delta并聯機器人結構參數Tab.1 Parameters of the Delta Parallel Manipulator

運用Matlab/Simulink中S-Function實現對RBF補償控制律的描述，用Matlab/Simmechanics描述被控對象。選取系統外部擾動為 τd=0.05+0.03*norm（e）+0.06*norm（e˙）。RBF 網絡的輸入為關節角度誤差狀態變量（x=［eT，e˙T］T）；隱層節點數為 5；節點中心［-0.04-0.02 0-0.02-0.04］；節點基寬度d=3；各節點初始權重取值0。分別在無外部擾動和有擾動兩種情況下進行計算力矩控制和RBF神經網絡在線補償控制算法對比，仿真結果，如圖5、圖6所示。仿真結果如圖，從圖3可以看出，在外部擾動為零時，計算力矩控制策略和RBF神經網絡在線補償控制策略都能較好的跟蹤期望軌跡，保障系統的穩定性。在加入外部擾動后，運動平臺軌跡跟蹤，如圖 4（a）、圖 4（b）所示。根據式（5），計算力矩控制策略穩態誤差不能收斂到0，因此不能很好的跟蹤末端平臺期望軌跡。對于RBF網絡在線補償控制，在系統仿真開始階段由于網絡在線學習自適應調整網絡權值，系統存在一定的波動。在權值逐漸逼近最優值時，跟蹤效果明顯好于一般的計算力矩控制策略，響應快速且穩定，具有較強的魯棒性。為更加直觀的對比仿真結果，分別給出在外部有界不確定擾動環境下X和Y方向的跟蹤誤差，如圖5、圖6所示。可以看出，計算力矩算法在系統穩定后誤差不能收斂為0且誤差波動幅度較大，而采用RBF在線補償控制律的控制效果明顯優于計算力矩控制，在線學習得到最佳網絡權值后，系統穩定且末端動平臺軌跡誤差的絕對值小于0.5mm，能夠很好的根據期望軌跡運動。

圖3 無擾動環境下軌跡跟蹤Fig.3 Trajectory Tracking without Disturbance

圖4 有擾動環境下Y方向軌跡跟蹤Fig.4 Trajectory Tracking with Disturbance

圖6 Y方向跟蹤誤差曲線Fig.6 Y Direction Tracking Error

5 結論

針對Delta并聯機器人控制過程中外部有界擾動、建模不準確等不可避免的不確定因素，結合計算力矩控制策略和RBF神經網絡在線補償控制策略，提出了一種基于計算力矩法的RBF神經網絡在線補償控制策略。采用RBF神經網絡在線調整隱層網絡權值，不斷逼近系統不確定項，并用Lyapunov理論證明系統穩定性及推導權值自適應律。根據給定的期望軌跡和機構參數，基于Simulink、Simmechanics建立Delta機器人控制系統聯合仿真模型。由仿真結果可以看出的控制策略可以很好的實現對目標軌跡的實時跟蹤，控制效果優于計算力矩控制，能夠有效保證Delta機器人系統穩定運行且穩態誤差小，較好的提升了系統的性能。

［1］宮赤坤，藍黎恩．Delta并聯機器人的動力學研究［J］．機械科學與技術，2013（12）：1780-1784．（Gong Chi-kun，Lan Li-en．Study on the dynamics analysis of delta parallel robot［J］．Mechanical ScienceandTechnology，2013（12）：1780-1784．）

［2］申鐵龍．機器人魯棒控制基礎［M］．北京：清華大學出版社，2000．（Shen Tie-long．Robust Control of Robot［M］．Beijing：Tsinghua University Press，2000．）

［3］楊曉鈞，龍億．計算力矩法的CMAC同步軌跡跟蹤控制與仿真［J］．哈爾濱工業大學學報，2013（7）：85-89．（Yang Xiao-jun，Long Yi．Synchronous trajectory tracking control and simulation of CMAC neural network based on computed torque control［J］．Journal of Harbin Institute of Technology，2013（7）：85-89．）

［4］賀紅林，何文叢，劉文光．神經網絡與計算力矩復合的機器人運動軌跡跟蹤控制［J］．農業機械學報，2013（5）：270-275．（He Hong-lin，He Wen-cong，Liu Wen-guang．Tracking control of robot using hybrid controller based on neural network and computed torque［J］．Transactions of the Chinese Society for Agricultural Machinery，2013（5）：270-275．）

［5］Linda O，Manic M．Evaluating uncertainty resiliency of type2 fuzzy logic controllers for parallel Delta robot［C］．IEEE 4thInternational Conference on Human System Interactions．Piscataway，USA：IEEE，201（5）：91-97．

［6］江道根，高國琴，胡紅玉．六自由度并聯機器人線性化反饋RBF神經滑模控制研究［J］．機械設計與制造，2010（2）：159-161．（Jiang Dao-gen，Gao Guo-qin，Hu Hong-yu．The study on parallel robot of RBF netrual sliding controller［J］．Machinery Design&Manufacture，2010（2）：159-161．）

［7］ParkJ，SandbergLW．Universalapproximationusingradial-basis-function networks［J］．Neutral Comput，1991，3（2）：246-257．

［8］劉金琨．機器人控制系統的設計與MATLAB仿真［M］．北京：清華大學出版社，2008．（Liu Jin-kun．Design and MATLAB Simulation of Roboticsystems［M］．Beijing：Tsinghua University Press，2008．）

［9］KatsuhikoOgata．ModernControlEngineering［M］．USA：PrenticeHall，2007．

［10］王英波，黃其濤，鄭書濤．Simulink和SimMechanics環境下并聯機器人動力學建模與分析［J］．哈爾濱工程大學學報，2012（1）：100-105．（Wang Ying-bo，Huang Qi-tao，Zheng Shu-tao．Dynamic modeling and analysis of a parallel manipulator using Simulink and SimMechanics［J］．Journal of Harbin Enginering University，2012（1）：100-105．）