微型快換拋投式偵查機器人跌落碰撞分析

李佳龍，劉滿祿，張俊俊，張 華

（西南科技大學 特殊環境機器人技術四川省重點實驗室，四川 綿陽 621010）

1 引言

隨著美國第一款用于軍工、反恐的Scout偵查機器人問世，國內外對微型偵查機器人的研究、應用逐漸重視。偵查機器人的任務主要在需要人參與的應急、反恐、災害等危險環境情況下進行偵查工作。隨著技術的進步和任務的多元化，具備較強功能的微型拋投式偵察機器人系統研究也開始成為新的研究熱點[1-3]。但是傳統微型偵查機器人的車輪不能根據場所時時迅速更換，機器人適應性不強。所以，文章特色在于研究一種車輪可以快速更換車輪的微型拋投偵查機器人，不僅可以在應急環境中通過手拋、槍射、炮射、空投或小型機器人攜帶等多種方式將機器人拋至預定場所，而且可以根據不同場所快速更換車輪已適應復雜環境。防碰撞能力的優劣直接決定了機器人的壽命，所以必須考慮機器人在拋投后落地碰撞時承受沖擊的能力。文獻[4-5]中都提到在沖擊物與受沖擊構件的接觸區域內應力狀態相當復雜，且沖擊持續時間非常短促使得接觸力隨時間的變化難以準確分析，這些都讓沖擊問題的精確求解十分困難。文獻[6]中總結了目前多體系統碰撞動力學分析方法中，建立數學模型的三種方法：沖量動量法，連續碰撞力模型，基于連續介質力學的有限單元法。其中使用沖量動量法雖然很簡單的就能估算出結果，但是前提是假設所有部件為剛體，不能滿足橡膠輪胎的柔性情況。使用連續介質力學的有限元方法計算出的結果最精準但是需要計算的工作量相對復雜而且繁重，所以文章采用簡單快捷的計算柔性連續多體碰撞動力學模型中的求解沖擊問題的能量方法，解決零件設計優化和估算拋投機器人跌落高度這個工程問題[7]。文章理論是基于能量守恒定理，即在不考慮摩擦等損耗外，動能和勢能轉化為系統內能。利用ANSYS/LS-DYNA模塊的顯示求解器求解碰撞沖擊這類瞬態多體動力學情況，從仿真實驗中對設計的拋投偵查機器人進行研究，分析各部件的防碰撞性能，進行實物設計的優化并且考察其使用的允許安全高度[8-11]。

2 快換結構及碰撞分析

微型車輪可快換拋投式機器人整體，如圖1所示。車輪外緣和車輪端面都采用HNBR橡膠減震且車輪上開有一定數量的減震孔，車軸處為45鋼，其余部分采用6061-T6鋁合金，尾巴由鋼絲制成。鋁合金6061抗拉強度σb≥240MPa，屈服強度σ0..2≥145 MPa，45 鋼抗拉強度 σb≥600MPa；屈服強度 σ0..2≥355MPa。根據實物測量可以知道：車總質量m≈1kg、車輪半徑R=40mm、輪轂半徑r=20mm、車輪橡膠寬度b=20mm、總長L=160mm。快換車輪結構爆炸圖和裝配圖，如圖2所示。其中1擋板；2卡子；3彈簧；4輪轂；5軸承端蓋；6車軸。快換結構主要利用了輪轂和輪軸部分。通過兩個卡子使得軸能在軸向上能夠限位或活動，彈簧讓卡子能夠處于閉合狀態。當需要更換不同類型車輪時，只需撥動兩個卡子，然后將輪轂（車輪與輪轂始終連接）拔出，裝輪子則只需直接將新的輪轂插入軸即可。這個快換結構能夠在不使用任何工具情況下快速方便地拆裝新的輪子，實現機器人在不同地域行動所需。在分析圖3可知，機器人碰撞受力都是在車輪的外側和上下側，幾乎不受內側向外側方向力的情況。當其在外側和上下側受力時分局部剖視圖，如圖3所示。輪胎受到的力傳遞到輪轂，輪轂受力直接傳到的是軸，卡子和軸的前端沒有受力，受力部位始終是圖3中右側小圓標示的軸與輪轂的接觸面。所以，當機器人著地時卡子和軸不會相互作用，機器人碰撞的受力分析只需考慮軸與輪轂，快換結構對其沖擊沒有影響。外部沖擊對快換結構只是輪轂內部卡子與軸之間存在較小的相互作用，這個相互作用是多體系統之間剛體與剛體或者剛體與柔性體之間產生的。作用力的大小只取決于快換結構之間的裝配關系和間隙的大小。在分析碰撞時，可以直接將快換結構簡化。

圖1 拋投偵查機器人Fig.1 Miniature Throwing Scout Robot

圖2 快換結構Fig.2 The Quickly ChangedStructure

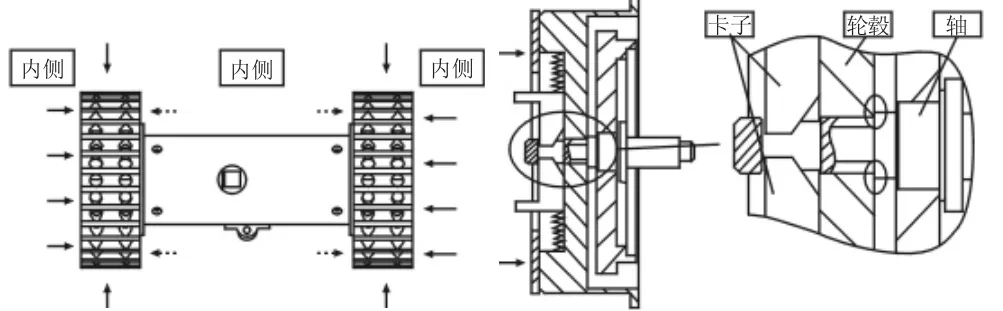
圖3 快換結構力學分析Fig.3 The Stress Analysis of Quickly Changed Structure

設橡膠車輪碰撞時候受全部六個應力分量 σx、σy、σz、τyz、τzx、τxz，根據能量守恒定理，形變勢能的多少與彈性體受力的次序無關，而完全取決于應力及形變的最終大小。認為所有應力分量和形變分量全部同時按同樣的比例增加到最后的大小，則得出全部應變能密度：v

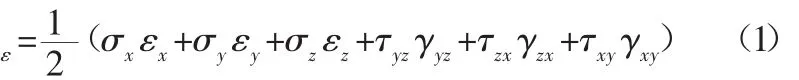
為了得到整個橡膠輪的形變勢能Vε，需將應變能密度vε在整個橡膠車輪的體積內進行積分，也就是：

以上分析是基于經典動力學理論的，而對于像這種機器人系統，由連接副連接起來的多個剛體組成的復雜多體系統，通過使用以上理論分析找到解析解或者近似解非常困難。但是，隨著計算機技術的不斷發展，很多軟件將各種算法集成到一起，所以應用計算進行輔助分析，已經成為一種針對多體系統分析的主要方式。在ANSYS中分析時碰撞前多體系統的動力學方程為：

式中：M—碰撞前系統的廣義質量矩陣；Φq—碰撞前系統約束的雅克比矩陣；λ—約束力矢量；Q*—由于動能相對時間求導得到的速度二次項；Qe—外力矢量；γ—加速度約束方程右端項；q—系統的廣義坐標列陣。碰撞階段動力學方程：

式中：M—總體質量矩陣；x（t）—總體節點加速度向量；P—由節點處載荷、內力、外力等形成的載荷向量，F—單元等效節點力向量（或稱應力散度）的組集；N—形函數矩陣；B—應變矩陣；σ—應力向量；H—控制由單點高斯積分引起的零能模態；C—結構黏性阻尼矩陣。

設小車質量為m，下落高度為h，車輪的最大變形為Δd，在材料滿足胡克定律的情況下，變形為Δd時彈力為Fd，橡膠彈性模量為E，以靜載mg作用在小車上的靜變形為Δst。忽略產生的熱能等，根據能量守恒定律，系統的變形前的能量總和等于彈性體變形后產生的應變能。所以通過能量方法有：

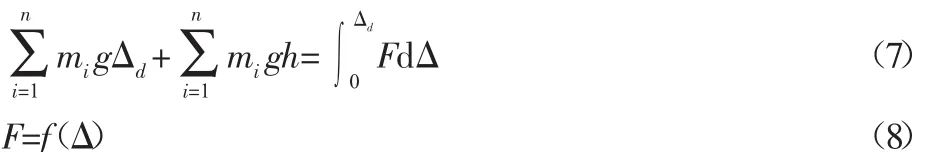
其中碰撞過程中各零件之間的連接狀態不變，在不損壞車體情況下，鋁合金相對與橡膠而言變形較小可忽略不計，車輪上橡膠的尺寸足夠大使得在碰撞過程中橡膠始終為彈性變形。

3 碰撞姿態仿真

設θ為機器人下落時軸線與水平面之間的夾角，如圖4所示。圖中：R—橡膠輪外徑；r—橡膠輪內徑；b—橡膠輪厚度；r1—輪軸與輪轂配合處半徑。當在相同高度跌落，在不同角度傾斜姿態時碰撞過程中機器人的質心C以變速向下運動，同時機器人還會以一定的角速度繞質心旋轉。所以機器人在墜地碰撞時可能狀態可分為三種情況：（1）水平狀態；（2）傾斜角 θ為銳角狀態；（3）垂直狀態。在PROE中簡化實體模型，將不重要的部件舍去以便減少仿真計算量。在ANSYS中三種姿態著地時候所有的內部接觸和邊界條件等均相同。ANSYS／LS-DYNA顯示動力學求解要求積分時間步長Δt必須很小（如1e-6s），如果超過結構最小周期的確定百分數，計算位移和速度將無限增加[20]。所以設定模型初速度為5 m/s、8 m/s、10 m/s、12m/s、15 m/s（相當于從高度 h≈1.25m、3.2m、5m、7.2m、11.25m處自由落體），從模型與地面接觸處開始仿真，減少仿真計算時間。

圖4 姿態傾斜角Fig.4 The Slope Angleof Robot When Impact

3.1 軸線水平和垂直落地姿態

θ為小銳角時橡膠輪的主要受力狀態為徑向受壓，考慮到θ為小銳角此時車輪軸線趨近于水平，將模型做適當的放大處理，認為在碰撞過程中橡膠始終承受徑向方向上的力F，所以等同于水平落地狀態。當θ為90°時機器人垂直下落，車輪端部橡膠受到壓縮。碰撞前的動能完全轉化為機器人系統內能，10 m/s速度下仿真實驗，如圖5所示。

圖5水平和垂直姿態仿真圖Fig.5 Horizontal and Normal Posture Simulation

圖5 中看到，橡膠輪很好的起到了緩沖減震的效果，模型在水平姿態仿真過程中，橡膠輪壓縮直至最大，然后輪轂內側、車軸、車軸和輪轂接觸處開始受力；垂直著地姿態仿真過程中，機器人車輪端面橡膠首先著地，壓縮厚度e后，地面與車輪轂接觸，產生剛性碰撞。從局部剖視圖可以看到，機器人壓縮階段結束瞬間，輪軸處的應力最大，分別為142.2MPa和81.67MPa都處于材料許用應力范圍內。

3.2 傾斜角為大銳角

同前面情況不同同，機器人著地受力更為復雜，存在軸向受壓和徑向剪切應力。θ為大銳角此時車輪軸線趨近于垂直。10m/s速度下仿真實驗，如圖6所示。模型分析知道由于橡膠輪胎寬度為20mm，傾斜著地時橡膠輪的減震有效體積相對較小，所以轉化為應變能的少，碰撞沖擊力作用在剛體系統部分大，相比前面兩種姿態時連接軸和輪轂之間的存在較大擠壓應力，因為機器人還存在一個顛覆力矩M的作用。此種姿態下最大應力為353.2MPa會對機器人產生了少許的損害。所以，針對這個情況，即可分析得出優化結論。在圖5、圖6所示的三種姿態的等效應力圖中，模型仿真運動過程某些時刻，特別是在恢復階段應力都發生了一些應力紊亂，顯然這與實際經驗得出的情況不相符。在結合實際、分析仿真和查閱資料后，發現這種情況與動力剛化現象相關，而且又由于拋投機器人是由多個剛體以及柔性體通過相應的裝配關系形成的復雜機械系統，在機器人碰撞過程中各部件之間存在非常復雜的相互作用。同時，機器人設計的軸和輪轂等的配合存在間隙，所以增大了應力紊亂現象。

圖6 傾斜姿態仿真圖Fig.6 Tilting Posture Simulation

3.3 對比試驗

仿真在 5m/s、8m/s、12m/s、15m/s初速度下實驗對比數據，如表1所示。用優化軸和橡膠車輪之后，在5m高度進行實物的跌落碰撞測試實驗，如圖7所示。表1的對比實驗數據得出，5m高度是這款機器人可能允許的最大安全高度。優化軸等部件后，實物跌落實驗，對比跌落前和跌落后快換結構的卡子、軸、輪轂等零部件的受損情況，實驗結果發現，卡子與軸裝配處沒有前后沒有任何變化，軸與輪轂結合處在優化了結構之后，也沒有損害。

表1 對比仿真實驗數據Tab.1 The Contrast Simulation Data

圖7 實物測試圖Fig.7 Physical Test

4 結論

通過仿真實驗得到，優化輪軸、輪軸和輪轂的接觸面可以降低機器人在碰撞過程中的應力集中；改變橡膠車輪的結構、尺寸，同樣可以增加抗沖擊能力。仿真實驗和實物實驗結果驗證了機器人在5m高度跌落后各個零部件沒有損害，也說明了創新設計的快換結構的在此款機器人上應用非常方便、可靠。優化之后，估算出這款機器人許用安全高度是5m左右（此處通過查閱相關資料后，考慮到機器人內部電子零部件在太大沖擊力下會損壞[10]）。如果只通過增加端部橡膠或者零部件的尺寸來增加機器人抗沖擊能力，這種方法會附帶的會增加機器人的質量且效果甚微，所以提出以下方案：

（1）增加車輪端部在軸向方向上的柔性。彈性變形問題中，增大靜變形，可降低K和Fd。這是因為靜變形的增大表示構件剛度較小，因而能更多地吸收沖擊的能量。通過改變橡膠結構形狀，通常情況下都會使得呈數量級的變化，不失為減小最大碰撞力的一種有效的方案。

（2）控制機器人的墜地位姿。通過改善機器人發射裝置，調整機器人的質量分布或者優化機器人的結構組成及其外部形狀，避免機器人以危險姿態墜地。

［1］Sascha A，Stoeter，Nikolaos Papanikolopoulos.Kinematic motion model for jumping scout robots［J］IEEE Transaction on Robotics，2006，4（2）：14-19.

［2］Andrew Drenner，Ian Burt，Tom Dahlin.Mobility enhancements to the scout robot platform［J］.IEEEInternational Conference on Robotics&Automation，2000，15（2）：293-308.

［3］楊怡蓓，孫濤，王萌.拋投式機器人碰撞參數分析及優化［J］.機電一體化，2008（6）：29-31.（Yang Yi-pei，Sun Tao，Wang Meng，Wei Yan-xia.Dumped robot collision parameters analysis and optimization［J］.Mechatronics，2008（6）：29-31.）

［4］徐芝綸.彈性力學（第四版）［M］.北京：高等教育出版社，2006.（Xu Zhi-lun.Elasticity（Fourth edition）［M］.Beijing：Higher Education Press，2006.）

［5］Tong Yan Tee，Jing-en Luan，Hun Shen Ng.A normal force-displacement model for contacting spheres accounting for plastic deformation：forcedriven formulation［J］.Journal of Applied Mechanics，2000，6（67）：363-371.

［6］董富祥，洪嘉振.平面柔性多體系統正碰撞動力學建模理論研究［J］.計算力學學報，2010，27（6）：1042-1048.（Dong Fu-xiang，Hong Jia-zhen.Dynamic modeling collisions theory on planarflexiblemultibodysystems［J］.JournalofComputationalMechanics，2010，27（6）：1042-1048.）

［7］郭安萍，洪嘉振，楊輝.柔性多體系統接觸碰撞子結構動力學模型［J］.中國科學，2002，32（6）：765-770.（Guo An-ping，Hong Jia-zhen，Yang Hui.Flexible multibody system dynamics model of contact-impact substructure［J］.Science in China，2002，32（6）：765-770.）

［8］蘇小平，朱健，王強.輕型客車車架正面碰撞仿真分析［J］.機械設計與制造，2010（11）：85-86.（Su Xiao-ping，Zhu Jian，Wang Qiang.Minibus frame frontal crash simulation analysis［J］.Mechanical Design and Manufacturing，2010（11）：85-86.）

［9］魏丕勇，閆清東，李宏才.履帶式移動機器人車體跌落碰撞仿真分析［J］.機械強度，2005，27（1）：12-16.（Wei Pei-yong，Yan Qing-dong，Li Hong-cai.Tracked mobile robot body fellcrashsimulationanalysis［J］.MechanicalStrength，2005，27（1）：12-16.）［10］Yiyi Ma，Kim-Yong Goh，Xueren Zhang.Board level drop test simulation using explicit and implicit solvers［J］.2014 IEEE 16th Electronics Packaging Technology Conference（EPTC），2014：671-677.