車輪踏面檢測自定心裝置的設計與研究

劉樂平，曾昭韋，鄒 歡，藺聰聰

（1.華東交通大學 機電與車輛工程學院，江西 南昌 330013；2.天津濱海快速交通發展有限公司，天津 300457）

1 引言

車輪在列車高速運行時與鐵軌直接接觸，其踏面質量直接關系到列車運行的安全性和平穩性[1-3]。如今車輪的生產已步入大批量自動化生產模式，單點、抽檢用的卡尺和卡規等人工測量方法[4-7]，已無法滿足秒計的生產節拍和復雜踏面檢測精度的要求，快而準、踏面自動檢測的方法需求迫切。

自動檢測時，傳感器均須分散布置在車輪踏面的外側，可采用傳感器旋轉或車輪旋轉。因傳感器旋轉時機構龐大，一般采用車輪旋轉，這就需要設計相應的車輪自定心裝置。輪對生產工藝中，車輪軸孔及其端面在與輪軸壓裝前才精加工，即車輪出廠前的軸孔及其端面等用作定位表面的部位誤差均較大，即使自定心裝置定心精度高，最終定位誤差也會較大。因此，設計快速高效的自定心裝置，在一定的定位誤差范圍內測出踏面參數真值，是車輪自動化生產中踏面自動檢測的技術關鍵。下面將介紹自定心裝置的設計，并以踏面半徑測量為例，通過模擬車輪軸線傾斜和偏心，建立測量的誤差模型，通過測得的踏面關鍵點數據，求得踏面的真值。

2 車輪踏面檢測自定心裝置的設計

2.1 踏面參數檢測原理

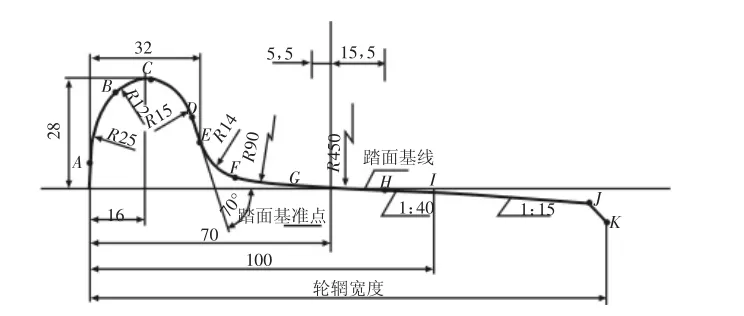
圖1 LMA型貨車車輪踏面形狀Fig.1 The Tread Profile Shape of LMA Wagon Wheel

車輪踏面外形輪廓，是由圓弧與圓弧或圓弧與直線相切的多段曲線組成的復雜集合體[6]，LMA型貨車車輪的踏面形狀，如圖1所示。在檢測時，通過對其關鍵點（圖中 A、B、C、D、E、F、G、H等）進行測量，然后對測量數據進行處理，得到車輪踏面參數值。

根據車輪旋轉式踏面檢測方案，檢測系統的組成和原理，如圖2所示。車輪落在自動定心裝置上，液壓系統控制液壓缸顫振使輪對完成定位，然后定心裝置帶動車輪旋轉，分散布置在車輪踏面外側的傳感器采集踏面關鍵點數據，通過數據測量采集系統送入計算機進行處理。

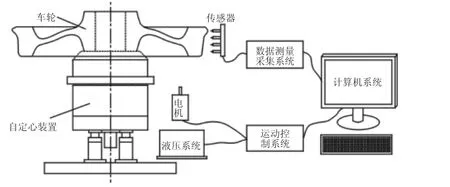
圖2 車輪踏面檢測系統示意圖Fig．2 The Schematic Diagram of Wheel Tread Detection System

2.2 車輪自定心裝置的設計

車輪踏面檢測自定心裝置關系到踏面參數檢測能否準確。為使車輪在檢測時快速準確定位，設計了的自動定心裝置，如圖3所示。在檢測工位時，同步液壓缸7推動托盤14升或降，使車輪脫離或送回車輪自動輸送輥道；車輪進入定心裝置后，由T形錐銷9粗定心，然后預振液壓缸6推動T形錐銷9顫振，使車輪精定心且輪轂端面與摩擦盤2接觸；定心裝置通過車輪自重產生的摩擦力矩帶動車輪旋轉，分散布置在車輪踏面外側的傳感器對踏面關鍵點進行檢測。

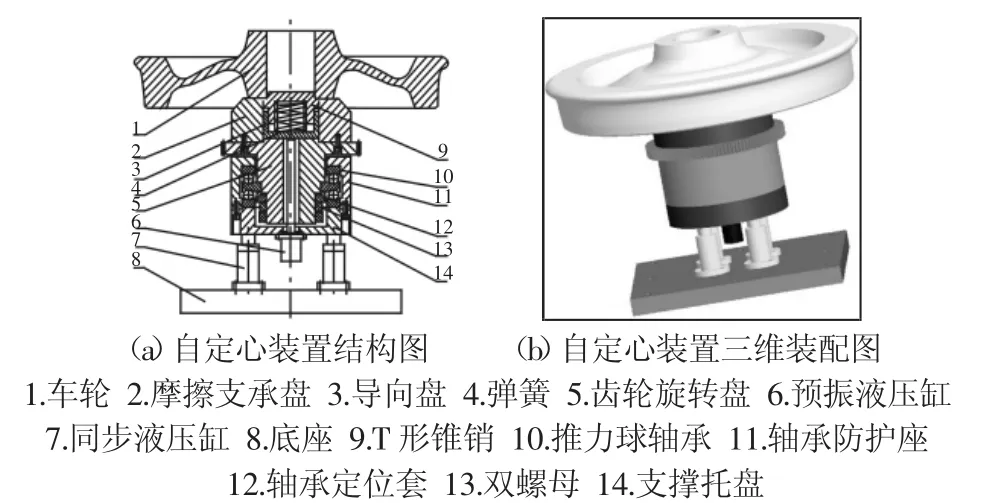
圖3 車輪踏面檢測自定心裝置Fig．3 The Self-Centering Device of Wheel Tread Detection System

2.3 啟動角加速度的計算分析

車輪的旋轉是靠其自身重力與摩擦支承盤產生的摩擦力矩帶動的，為保證車輪在啟動瞬間與摩擦支承盤不發生相對滑動，需對裝置旋轉啟動時的相關受力進行計算分析驗證。

2.3.1 車輪的摩擦力矩和轉動慣量的計算

以LMA型貨車車輪為例。設車輪總質量為m，輪轂半徑為R，輪轂孔半徑為r，材料為CL65。則車輪自重FN：

可得車輪對摩擦盤壓強為p=FN/（πR-πr），輪轂端面與摩擦盤的摩擦系數與材料有關，還與表面粗糙度有關。摩擦盤選材為NM360耐磨抗沖擊型鋼，粗糙度為Ra25μm，輪轂端面粗糙度為 Ra12．5μm，則二者間無潤滑的靜摩擦系數 f=（0．15～0．2）。摩擦力矩

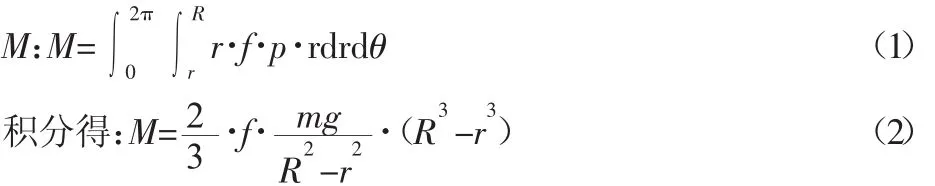
由于車輪結構復雜，轉動慣量計算較難，故運用統計學原理對其剖面進行分割，取相對值計算。如可將LMA型車輪剖面劃分成5700個單元，其中輪轂部分2010個單元，輪輞部分1420個單元，輻板部分2270個單元。以車輪幾何中心作為轉動慣量的質心，則轉動慣量Ji：

式中：i=1、2、3，分別對應于輪轂、輪輞、輻板；ri1、ri2—它們的內、外

計算半徑；ki—第i部分的質量比。分別求得三部分轉動慣

量 J1、J2和 J3，則總轉動慣量 J：

綜上所述，根據旋轉力矩、轉動慣量和啟動角加速度的關系：M=J·α，計算得出自定心裝置的啟動角加速度α。

2.3.2 啟動角加速度的仿真分析

以LMA型貨車車輪為例，建立車輪和自定心裝置的三維模型，并導入到ADAMS軟件中，通過設置相關參數，得出車輪啟動摩擦力與啟動角加速度關系的分析結果。

由于車輪是與摩擦支承盤接觸產生的摩擦力矩，為簡化結構，便于參數的設置，在此只導入車輪與摩擦支承盤的裝配體，在摩擦支承盤的旋轉軸上施加旋轉副，并在車輪上設置摩擦副，如圖4所示。

圖4 車輪與摩擦盤裝配體參數設置Fig．4 Parameter Setting of the Assembly Body Between the Wheel and Friction Disk

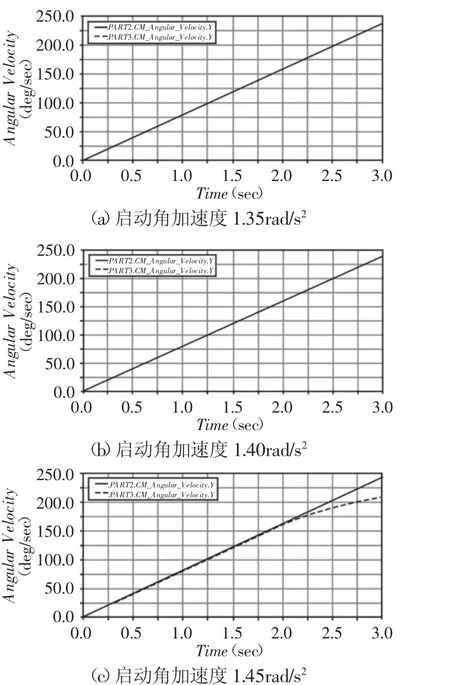
圖5 不同啟動角加速度的仿真結果Fig．5 The Simulation Results of Different Starting Angular Acceleration

通過設置摩擦盤的不同啟動角加速度、車輪與摩擦盤間的摩擦系數等，得出車輪與摩擦盤之間的角速度-時間關系曲線，如圖5所示。

由圖5可知，當車輪與摩擦支承盤同步旋轉時，摩擦支承盤的啟動角加速度應小于其臨界值（即1.40rad/s2）；反之，車輪與摩擦支承盤產生相對滑動，車輪定位將不準確，測量結果將受影響。因此，應使自定心裝置的啟動角加速度不大于其臨界值，同時，為適應生產節拍要求及提高檢測效率，應選擇合適的啟動角加速度值。

3 踏面半徑測量的誤差建模

踏面半徑檢測時，車輪軸線的傾斜和偏心會影響其測量結果，采用合適的處理模型和算法對所測數據進行處理，得出車輪踏面參數值是至關重要的。

3.1 擬圓偏心模型

由于車輪本身因素及測量時定位精度等影響，踏面檢測時，旋轉中心與車輪軸線可能存在傾斜或偏心等情況，導致傳感器所采集的數據存在偏差，從而對測量結果產生影響。為分析因車輪軸線傾斜或偏心引起的測量誤差，建立踏面擬圓偏心模型，采用最小二乘擬圓偏心法對其數據進行處理[8-10]，根據所測數據求得踏面的半徑值。車輪踏面檢測偏心示意圖，如圖6所示。通過設定傳感器的采樣頻率，對踏面進行等角度采樣及數據處理，從而得到車輪踏面參數值。

圖6 車輪偏心示意圖Fig.6 Schematic Diagram of the Wheel Eccentricity

3.2 最小二乘擬圓法

設定偏心圓方程[8]：

式中：a0、b0—最小二乘擬圓圓心坐標；R—最小二乘擬圓半徑。

由于誤差的存在，各測量點（xi，yi）不能完全滿足式（5），記半徑差為Si，則：

令 Si的平方和為 S1，由于 a0，b0，R 不是關于（xi，yi）的顯函數，不能直接求出a0，b0，R的值，引出平方差之平方和S2的方程：

令數學模型為：Σ［R2-（xi-a0）2-（yi-b0）2］2=min

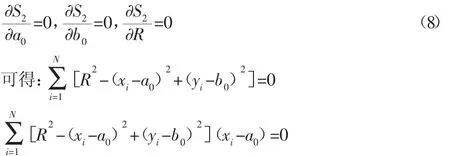
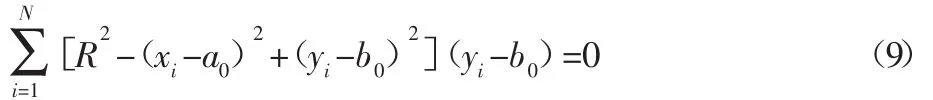
解上述方程即可得到車輪踏面的半徑值。

3.3 踏面參數模擬檢測分析

以LMA型貨車車輪為例，建立車輪的三維實體模型，對其踏面關鍵點橫截面進行分割，分別設置車輪軸線與測量平面傾斜1°（記為軸線傾斜1），車輪軸線與測量平面傾斜2°（記為軸線傾斜2），車輪軸線傾斜1°與車輪整體偏心5mm（記為軸線傾斜偏心），以及車輪整體偏心5mm（記為整體偏心）等情況，利用CAD軟件提取車輪踏面關鍵點的采樣數據，并對其采樣數據進行分析，得到表1的踏面測量點模擬測量結果和表2的踏面測量點誤差結果；繪制如圖7的車輪踏面關鍵點模擬測量結果圖和圖8的踏面測量點誤差圖。

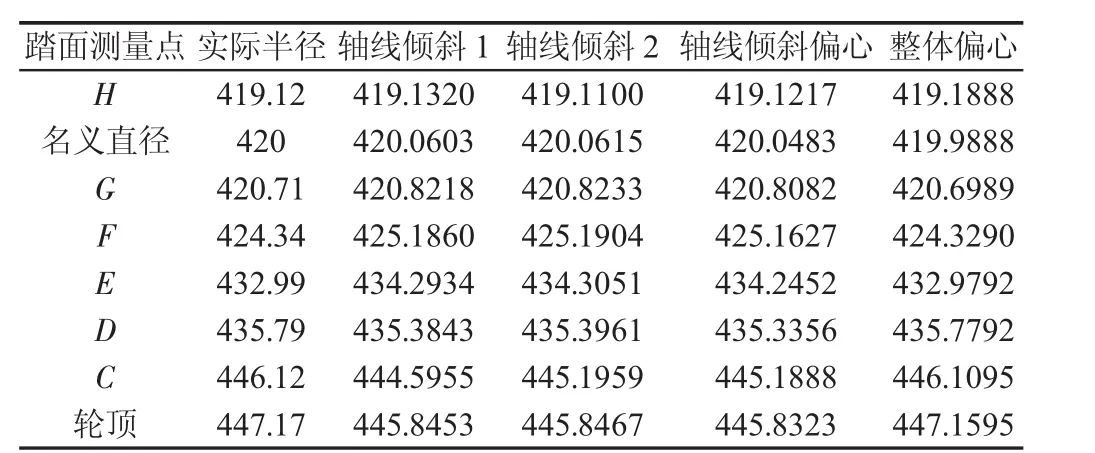
表1 車輪踏面測量點模擬測量結果（mm）Tab.1 Simulation Measuring Results of the Points of Wheel Tread

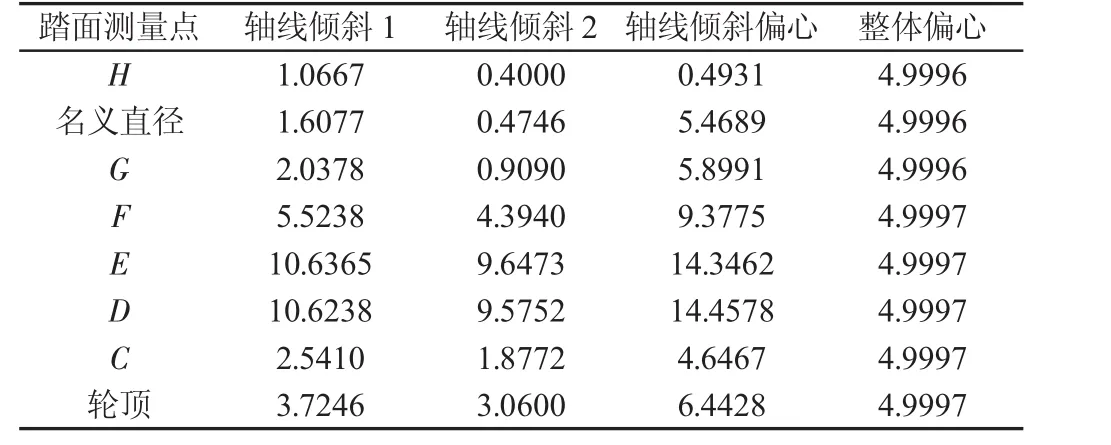
表2 車輪踏面測量點模擬測量誤差（mm）Tab.2 Simulation Measuring Errors of the Points of Wheel Tread

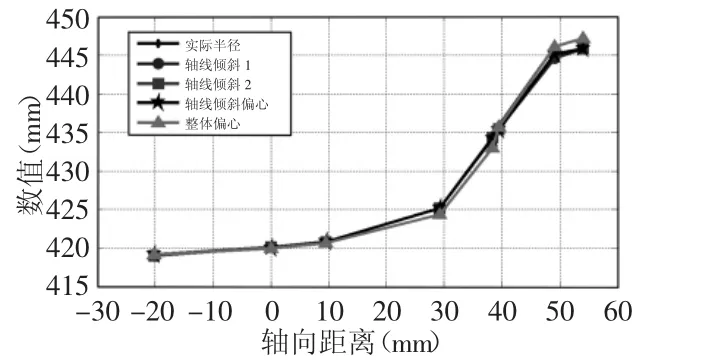
圖7 車輪踏面測量點模擬測量結果圖Fig.7 Diagrammatic Sketch of the Profile Point Measuring Results

圖8 車輪踏面測量點模擬測量誤差圖Fig.8 Error Diagrammatic Sketch of the Profile Point Measurement

通過仿真可知，假設車輪軸線傾斜和偏心，則車輪的實際值和測量值存在一定的偏差。由圖8踏面測量點誤差圖可得，在車輪軸線傾斜時，車輪踏面關鍵點測量誤差系數較大，尤其是在車輪輪緣部分，因其型面的自身特點，且車輪徑向尺寸較大，導致其在軸線較小傾斜的情況下產生較大的數值變化，從而導致測量誤差系數變大。在有車輪偏心時，誤差系數也會相應變大，但由于車輪偏心是其在測量平面內的偏心，其測量誤差值基本不變，數據處理時可用最小二乘擬合算法在一定程度上進行相應的補償。自定心裝置的使用主要是減小車輪軸線傾斜和偏心程度，使車輪在測量時精確定位，使測量的數值更接近車輪本身的實際尺寸。

4 結論

針對車輪踏面參數檢測系統，設計了一種車輪踏面參數檢測用自定心裝置，結合該自定心裝置，給出了踏面半徑測量的數據處理模型和計算方法，利用ADAMS軟件仿真分析了該自定心裝置啟動角加速度選擇的允許值，并對車輪踏面測量點進行了模擬測量分析。從仿真和模擬測量結果可得，自定心裝置的啟動角加速度應不大于1.40rad/s2；被測車輪踏面測量值的準確度在很大程度上受車輪軸線傾斜與偏心的影響，在自定心裝置的啟動角加速度及測量允許范圍內，采用車輪踏面參數檢測用自定心裝置，使車輪在檢測前進行精確定位，以減小車輪軸線的傾斜及偏心，從而減小車輪踏面檢測系統的測量誤差，可提高檢測的準確性。

［1］趙菊靜，范忠勝，方鳴.多功能車輪輪緣踏面自動化動態檢測系統［J］.現代城市軌道交通，2007（3）：5-7.（Zhao Ju-jing，Fan Zhong-sheng，Fang Ming.Multi-function automatic dynamic detection system of wheel-flange tread［J］.Modern Urban Transit，2007（3）：5-7.）

［2］洪明虎，黃志輝，鄭澤曄.火車車輪全模鍛數值模擬［J］.機械設計與制造，2011（7）：257-259.（Hong Ming-hu，Huang Zhi-hui，Zheng Ze-ye.Numerical simulation of whole die forging for railway wheel［J］.Machinery Design&Manufacture，2011（7）：257-259.）

［3］高向東，吳乃優，敖銀輝.鐵路車輛輪對自動檢測系統的研制［J］.機車電傳動，2003（2）：36-39.（Gao Xiang-dong，Wu Nai-you，Ao Yin-hui.Development of automatic wheelset detection system of wagon［J］.Electric Drive for Locomotives，2003（2）：36-39.）

［4］馬龍深，姜濤，張桂林.列車車輪直徑在軌動態檢測的研究［J］.長春理工大學學報：自然科學版，2014（2）：42-45.（Ma Lone-shen，Jiang Tao，Zhang Gui-lin.Research on dynamic testing of train wheel diameter in-orbit［J］.Journal of Changchun University of Science and Technology：Natural Science Edition，2014（2）：42-45.）

［5］向華，周力，梁志鋒.火車車輪踏面快速檢測系統的研究［J］.機床與液壓，2005（6）：121-122.（Xiang Hua，Zhou Li，Liang Zhi-feng.Research on rapid inspection system for the profile surface of the train wheel［J］.Machine Tool&Hydraulics，2005（6）：121-122.）

［6］敖銀輝，徐曉東，吳乃優.用激光位移傳感器檢測輪對踏面缺陷［J］.西南交通大學學報，2004，39（3）：345-348.（Ao Yin-hui，Xu Xiao-dong，Wu Nai-you.Defect detecting of train wheelset tread surface with laser displacement sensor［J］.Journal of Southwest Jiao Tong University，2004，39（3）：345-348.）

［7］馬林.車輪踏面外形幾何參數的檢測技術［J］.國外鐵道車輛，1998（6）：40-42.（Ma Lin.Detection technology in geographic parameters of the wheel tread profile［J］.Foreign Rolling Stock，1998（6）：40-42.）

［8］葛磊，鄒鯤.基于 MATLAB 的圓度誤差分析［J］.機床與液壓，2011（22）：99-101.（Ge Lei，Zou Kun.Roundness error analysis based on MATLAB［J］.Machine Tool&Hydraulics，2011（22）：99-101.）

［9］陳國鋒，王捷，鐘曉波.車輪踏面外形測量的數值處理［J］.城市軌道交通研究，2014，17（1）：78-82.（Chen Guo-feng，Wang Jie，Zhong Xiao-bo.Data processing for wheel/rail profile measurement［J］.Urban Mass Transit，2014，17（1）：78-82.）

［10］雷賢卿.基于誤差分離的圓柱度精密測量技術研究［D］.西安：西安理工大學，2007.（Lei Xian-qing.Study of the cylindricity precision measurement technique based on the error separation method［D］.Xi’an：Xi’an University of Technology，2007.）