動力學特性的礦井提升機載荷辨識研究

時安琪 ，任 芳 ，楊兆建 ，馬金山

（1.太原理工大學 機械工程學院，山西 太原 030024；2.煤礦綜采裝備山西省重點實驗室，山西 太原 030024）

1 引言

伴隨著礦山機械的發展和技術的進步，礦井提升機也正朝著大型、高速、重載與智能化的方向發展，對礦井提升機的工作性能也提出了越來越高的要求[1]。在多數情況下，由于受技術條件和工作環境的限制，作用在礦井提升機上的動載荷難以直接測量，但是相對而言，提升機在動載荷作用下的動態響應是比較容易測得的。探索用動力學的方法研究提升機載荷辨識問題，即根據結構在動載荷作用下的動態響應來確定動載荷的過程[2]。探索通過動力學特性辨識提升機系統動載荷的方法，為提升機系統動力學設計和故障診斷等提供依據。

2 模型的簡化與建立

2.1 物理模型的簡化

礦井提升機的傳動系統是由電機、減速器與主軸裝置組成，由聯軸器連接的傳動系統，其系統的本質是一個多支撐多圓盤的轉子系統。目前，傳遞矩陣法是計算多支撐多圓盤轉子系統轉子動力學問題的一種有效方法。根據轉子系統動力學傳遞矩陣法的假設：圓盤是有質量和轉動慣量而無厚度無變形的剛性薄圓盤，軸段是有剛度和長度而無質量的彈性軸[3]。把電機、減速器、以及主軸裝置進行質量集中，等效為剛性薄圓盤，得到三自由度轉子系統。由于減速器為齒輪傳動，所以傳動系統為齒輪傳動軸系，傳動系統可簡化為等效直列軸系[4]。把齒輪系等效到電機上，得到兩自由度轉子系統示意圖，如圖1所示。

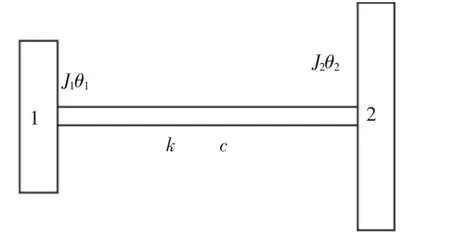
圖1 兩自由度模型Fig.1 2-Degree Model

圖中：1、2—電機、主軸裝置等效圓盤；J1、J2—1、2 等效轉動慣量；

θ1、θ2—1、2 角位移；k—等效剛度；c—等效阻尼。

2.2 數學模型的建立

運用拉格朗日方程是求解復雜剛體動力學問題的一種有效方法，特別的適于物理理論的研究。把轉子系統看做一個整體，結合系統的動能和勢能，由拉格朗日方程針對三自由度物理模型建立系統的三自由度運動微分方程數學模型[5]為：

兩自由度物理模型建立兩自由度運動微分方程數學模型為：

式中：M1—電機施加的驅動扭矩載荷；M2—制動器施加在主軸裝置上的干擾力矩載荷。

3 Matlab/Simulink仿真

根據數學模型，利用Matlab/SimilinkLibrary的模塊建立仿真模型，為避免復雜的連線，增強模型的可讀性，對仿真模型進行封裝，用Goto模塊進行數據傳輸[6]，仿真模型，如圖2所示。圖中黃色部分為電機模型，灰色部分為轉子系統機械傳動模型，Subsystema為兩自由度的機械模型，Subsystemb為三自由度機械模型。仿真時間設置為10s，系統運行穩定以后開始加載干擾力矩，加載信號為頻率10Hz，幅值10N．m，偏移量10N．m的正弦載荷，加載時間為（5～10）s。電機及主軸裝置等效角速度在兩自由度和三自由度模型的仿真后對比圖像和加載后驅動力矩變化情況，如圖3所示。由圖3可看出加載后兩種模型在運行穩定以后運動狀態基本保持一致（ω1、ω3分別為兩自由度、三自由度模型電機角速度，ω2、ω4分別為兩自由度、三自由度模型主軸裝置等效角速度），表明可以用兩自由度的模型來代替三自由度模型簡化分析。

圖2 轉子系統機電仿真模型Fig．2 Mechanical and Electrical Simulation Model

圖3 加載后曲線變化Fig．3 Curves Variation after Loading

4 支持向量機回歸分析與載荷識別

4.1 支持向量機模型的構建

支持向量機在回歸分析中，參數的選取，尤其是懲罰參數c與核函數參數g的選取，對模型回歸的精度影響很大。僅采用經驗法，能得到精度較大的回歸結果，但是很難得到最優的結果，這里采用遺傳算法尋優來選取c、g值，以得到最佳輸出[7-9]。支持向量機的輸入為電機與主軸裝置角速度構成的二維數據，輸出為載荷構成的一維數據；采用最大最小法把數據歸一到［-1，1］區間內，避免各維數間數據過大的數量級；采用pca降維的方法把數據全降為一維數據，便于分析；采用交叉驗證的方法對SVM中懲罰參數c與核函數參數g進行評估，遺傳算法的適應度函數值則選取交叉驗證中計算得到的每組懲罰參數c與核函數參數g，從而在一定的區間內全局尋優，得到最佳c、g值[10]。采用5折交叉驗證，設置種群數量10，進化代數100[10]，得到制動力矩-適應度曲線，如圖 4（a）所示。最佳 c=54．773，g=99．3569，交叉驗證的均方誤差為0．013909，得到的參數值較好；采用同樣的模型以及參數設置得到驅動力矩-適應度曲線，如圖4（b）所示。最佳c=11．1771，g=50．1154，交叉驗證的均方誤差為0，得到的了最佳值。

圖4 適應度曲線Fig．4 Fitness Curves

4.2 支持向量機的識別結果

對于制動力矩，輸入選取（6～7）s的前兩個周期的 ω1與 ω2，輸出為相應的制動力矩載荷值，用訓練制動力矩時的最佳的c、g值，結合支持向量機模型，計算得到載荷的原始曲線與回歸曲線對比圖，如圖 5（a）所示。均方誤差為 0．0094396，相關系數 r2=0．99339，表明回歸模型性能較好。（6～7）s的第三個周期的載荷真實值與識別值的對比圖，如圖5（b）所示。均方誤差為0．008904，相關系數r2=0．99445，角速度與制動力矩的真實值、識別值的對比，如表1所示。最大誤差為1．005N．m，識別效果較好，表明該模型對礦井提升機制動力矩載荷具有良好的學習能力和識別能力。對于電機的驅動力矩，輸入選取（6～7）s的前兩個周期的ω1與ω2，輸出為相應的驅動力矩載荷值，利用訓練驅動力矩時的最佳的c、g值，結合上述相同的支持向量機模型，計算得到載荷的原始曲線與回歸曲線對比圖，如圖6（a）所示。均方誤差為 0．0096683，相關系數 r2=0．98756，表明回歸模型性能較好。（6～7）s的第三個周期的載荷真實值與識別值的對比圖，均方誤差為 0．0097938，相關系數 r2=0．98916，如圖 6（b）所示。

圖5 制動力矩的回歸與識別Fig．5 Regression and Recognition of Braking Torque

表1 角速度、制動力矩真實值與識別值Tab.1 The Angular Velocity，the Real Value and Recognition of Braking Load

圖6 驅動力矩的回歸于識別Fig．6 Regression and Recognition of Driving Torque

角速度與驅動力矩的真實值、識別值的對比，如表2所示。最大誤差為0．070N．m，識別效果良好，表明該模型對礦井提升機驅動力矩載荷具有良好的學習能力和識別能力

表2 角速度、驅動力矩真實值與識別值Tab.2 The Angular Velocity，the Real Value and Recognition of Driving Load

5 結論

（1）根據傳遞矩陣法原理合理簡化了礦井提升機傳動系統，并建立了兩自由度和三自由度的運動微分方程。（2）通過仿真分析結果，兩自由度模型與三自由度模型在運行穩定以后運行狀態基本一致，可以用兩自由度的模型代替三自由度模型以簡化分析。（3）用遺傳算法優化的支持向量機對制動力矩與驅動力矩進行了載荷辨識，相關系數分別為0．99445與0．98916，識別結果良好。表明支持向量機可以對礦井提升機載荷作定量識別。

［1］嚴世榕，聞邦椿．礦井提升系統的動力學研究［J］．金屬礦山，1998（5）：31-33．（Yan Shi-rong，Wen Bang-chun．Investigation on the dynamics of the winding system in mine shaft［J］．Metal Mine，1998（5）：31-33．）

［2］楊智春，賈有．動載荷識別方法的研究進展［J］．力學與實踐，2015（1）：164．（Yang Zhi-chun，Jia You．The research progress of dynamic load identification method［J］．Mechanics in Engineering，2015（1）：164．）

［3］袁慧群．轉子動力學基礎［M］．北京：冶金工業出版社，2013．（Yuan Hui-qun．Rotor Dynamic Foundation［M］．Beijing：Metallurgical Industry Press，2013．）

［4］方同．振動理論及應用［M］．西安：西北工業大學出版社，2002．（Fang Tong．Vibration Theory and Application［M］．Xi’an：Northwestern Polytechnical University Press，2002．）

［5］恒放．礦井提升機的動載響應研究［D］．重慶：重慶大學，2010．（Heng Fang．Research on dynamic response of mine hoist［D］．Chongqing：Chongqing University，2010．）

［6］翟亞寧，楊兆建．基于小波包能量譜和BP神經網絡的轉子系統扭矩激勵識別［J］．中國農機化學，2015（3）：194-198．（Zhai Ya-ning，Yang Zhao-jian．Torque incenrive identification of the rotor system based on wavelet packet energy spectrum and BP neutral network［J］．Journal of Chinese Agricultural Mechanization，2015（3）：194-198）

［7］Xu Chun-bi，Liu Jing-cheng，Li Jun．Forecast model for gas well productivity based on GA and SVM［J］．Applied Mechanics and Materials，2011（8）：4958-4962．

［8］Jiang Xue-peng，Dai Yu-jin，Hong Bei．SVM model based on GA optimization for inertial prediction［J］．Journal of Nanjing University of Science and Technology，2011（7）：34-39．

［9］曹善成，宋筆鋒，殷之平．基于支持向量機回歸的飛行載荷參數識別研究［J］．西北工業大學學報，2013（4）：535-539．（Cao Shan-cheng，Song Bi-feng，Yin Zhi-ping．Study on flight load parameter identification based on SVM［J］．Journal of Northwestern Poytechnical University，2013（4）：535-539．）

［10］史峰，王小川，郁磊．MATLAB 神經網絡30個案例分析［M］．北京：北京航空航天大學出版社，2010．（ShiFeng，WangXiao-chuan，YuLei．ThirtyNetworkCasesAnalysisBased on MATLAB［M］．Beijing：Beijing University of Aeronautics and Astronautics University Press，2010．）