桿式超聲電機頻率一致性設計關鍵問題研究

胡 斌，董亞東，陶 征

（鄭州大學 機械工程學院，河南 鄭州 450001）

1 引言

超聲電機具有低速大力矩、響應快、分辨率高和抗電磁干擾等優點[1]。作為一種全新概念的直接驅動裝置，超聲電機在航空航天、機器人以及微型機械等領域得到了成功應用。作為超聲電機中的重要一類，桿式多自由度超聲電機除具有上述一般超聲電機的特點之外，由于能夠提供兩個或兩個以上自由度的運動，以及靈活的結構形式和驅動方式，從而成為當前壓電超聲電機領域里的一個研究熱點。桿式多自由度超聲電機利用壓電陶瓷逆壓電效應激發出的縱、彎兩種異形模態實現電機動力輸出[2-4]。然而，根據振動理論，兩種異形模態在同一等截面直桿中頻率一般是不相等的。為使縱、彎兩個振動模式能在同一激勵信號作用下達到共振狀態，實現電能對機械能的最大轉換，確保縱、彎兩個工作模態頻率具有較高的一致性，詳細闡述了桿式超聲電機頻率一致性設計中遇到的三項關鍵技術：電機振子設計要求及其結構形式的確定；壓電陶瓷片在桿式超聲電機振子中的最佳安放位置；基于螺栓聯接非線性系統的桿式超聲電機精確有限元模型。實驗驗證得到了較好的整機性能。

2 電機振子設計要求及結構形式確定

桿式多自由度超聲電機其工作原理，如圖1所示。三組壓電陶瓷片（PZT）A、B、C用于激發定子的三個工作模態：一個一階縱振模態和兩個二階彎振模態。通過模態運動的合成，定子端面任一質點形成橢圓軌跡運動，轉子在自重或負載力矩作用下通過與定子的摩擦接觸實現繞相應軸的轉動。

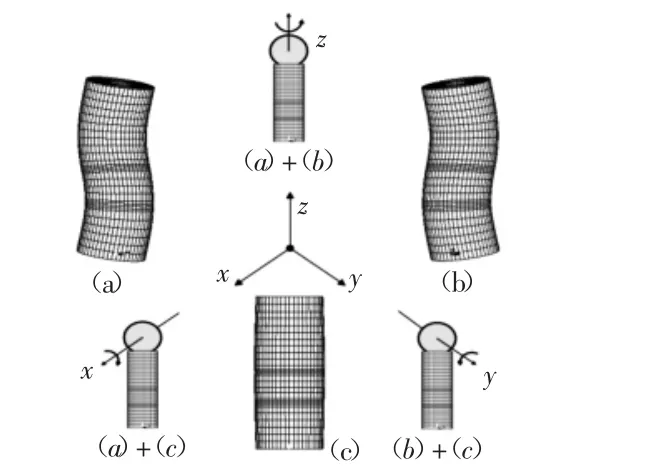
圖1 電機工作原理Fig.1 The Operating Principle Diagram of the Motor

根據上述電機驅動原理，電機振子設計應滿足要求：

（1）縱振、彎振頻率要保持良好的一致性；

（2）盡可能使振子頭部有更大的振幅[5-7]。

然而，在等截面圓柱定子中縱、彎兩種振動模態是很難保持頻率一致性的。等截面梁彎曲自由振動的微分方程和自由振動固有頻率分別為：

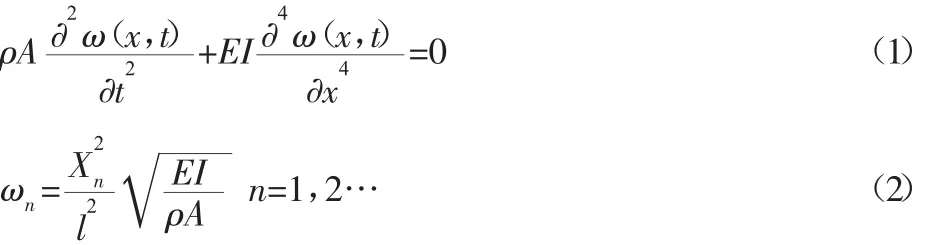
又由振動理論，等截面圓柱體直桿縱向自由振動微分方程和自由振動固有頻率為：

由此我們可以看出，為確保電機工作在兩種工作模態的諧振下，必須對電機振子進行合理的設計。研究表明，在桿式超聲電機定子體開環形槽，能夠改變定子質量以及剛度分布，進而保證縱、彎模態頻率一致性，增大定子頭部振幅。根據電機振子邊界條件，設計電機振子動力學有限元模型，該動力學模型材料屬性，如表1所示。電機定子、壓電陶瓷片分別選用八節點SOLID45單元和SOLID5三維耦合場體單元。

表1 材料參數Tab.1 The Material Parameters

在電機振子結構設計中，利用ANSYS有限元軟件進行設計建模與模態頻率一致性分析，找到了電機振子體上合理的開槽位置，反復計算分析凹槽結構參數對縱、彎振模態頻率的影響程度，發現：（1）環形槽Ⅰ、Ⅱ、Ⅲ（參見圖2）均使定子的二階彎頻和一階縱頻降低；（2）振子的內徑對二階彎振、一階縱振的影響均不大，槽Ⅰ對二階彎振影響大，槽Ⅱ、Ⅲ對一階縱振影響大；（3）環形槽的寬度對以上頻率均有一定影響，但三者變化的靈敏度基本相當，故不能通過改變環形槽寬度縮小縱、彎頻率差，而應改變環形槽深度及開設位置。據此，經多次試算最終確定了滿足要求的電機動力學有限元模型，其結構尺寸，如圖2所示。

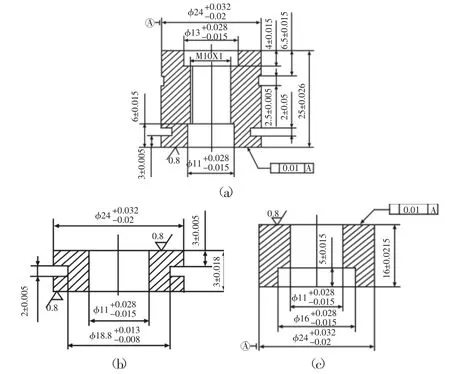
圖2 電機振子結構尺寸Fig.2 The Structural Parameters of the Motor Vibrator

3 壓電陶瓷片在振子中最佳安放位置

壓電材料作為桿式超聲電機中的關鍵元件之一，是將壓電陶瓷的電能轉換為機械能的核心部分，其安放位置的選擇直接決定整個超聲電機的動力輸出性能。桿式多自由度超聲電機的激勵二階彎振和一階縱振的三組壓電陶瓷片安裝布局，如圖3所示。其中每組三片，兩片工作片，一片檢測片（或電極片）；二階彎振陶瓷片組A、B每一片壓電陶瓷分為二個極性相反的區，通以高頻交流電后，一區伸長，另一區收縮，同理當施加高頻交流電正負號改變，其變形正好相反；一階縱振陶瓷片組C每一片壓電陶瓷極性相同。壓電元件的最佳安放位置是各自所激發出振型的節平面處[8-9]。這樣可以使壓電元件的振動能量最有效地傳遞給振子。對于桿式多自由度超聲電機來說，其采用一階縱振、二階彎振模態的工作模態頻率，在有限元分析中，筆者發現，基于上述結構設計的振子有限元模型，對于其一階縱振模態，應變最大位于其節點位置；對于其二階彎振模態，應變最大處于其波峰（或波谷）位置。由此，在振子動力學設計時，得到了基于上述結構形式（圖2）的振子壓電陶瓷片安放位置，即在縱振模態的節點和彎振模態的波峰（或波谷）處應分別安放縱振、彎振壓電陶瓷片。有限元模型各階振型，如圖4所示。基于上述振子設計結構尺寸加工、制造的樣機振子工作模態頻率，如表2、圖5所示。

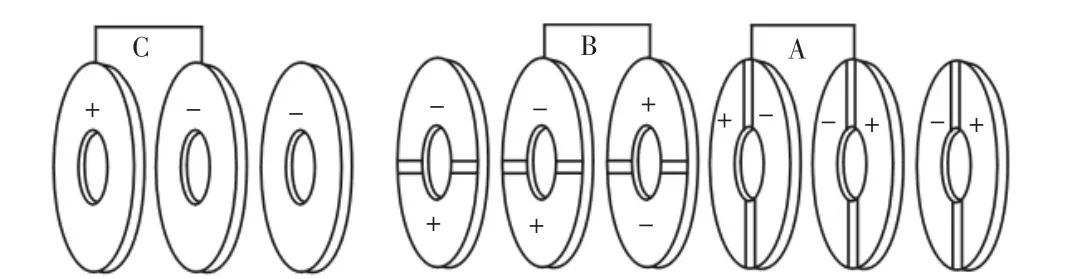
圖3 壓電陶瓷片安裝布局圖Fig.3 The Installation Layout Diagram of Piezoelectric Ceramics

圖4 有限元模型各階振型圖Fig.4 The Vibration Modes Diagram of the Contact Model

表2 樣機振子工作模態頻率（Hz）Tab.2 The Working Mode Frequency of the Prototype Motor Vibrator（Hz）

圖5 樣機振子掃頻及定頻測試結果Fig．5 Frequency Reponses From Laser Vibrometer

4 螺栓聯接非線性有限元模型

桿式多自由度超聲電機振子采用蘭杰文振子結構形式，由螺栓將金屬彈性體頭部、下部、尾部、三組壓電陶瓷片緊固為一體。有螺栓聯接必然存在聯接面的接觸[10]。螺栓聯接結構非線性問題主要源于聯接面接觸、摩擦等。接觸是螺栓聯接的基本特征，而接觸剛度作為結構整體剛度重要組成部分對其動力學特性影響很大，故在有限元動態建模過程中需考慮這一非線性本質問題；其次，螺栓聯接結構往往需要施加預緊力/力矩，其值大小直接決定聯接面接觸狀態。在預緊力/力矩載荷作用下，電機振子各元件之間通過聯接面接觸和摩擦傳遞力/力矩，因此，預緊力和摩擦系數的影響必須考慮在內。有上述分析，建立的基于螺栓聯接非線性系統的電機振子有限元模型，共有35727個單元，50380個節點。其中，采用預緊力單元PRETS179施加預應力3000N；采用目標單元TARGE170模擬剛性目標面，接觸單元CONTA174模擬柔性接觸面，依次建立金屬彈性體與壓電陶瓷片、螺栓之間的接觸行為；法向接觸剛度設置 8．56（介于 0．01～10），摩擦系數設置為0．14；螺栓單元類型SOLID45，材質為45#；邊界條件兩端自由。首先在考慮接觸特性及預緊力的情況下，完成靜態非線性分析進而把獲得的應力以附加剛度的形式疊加到電機振子整體結構之上，然后對帶有附加剛度的電機振子進行模態分析，得到各階工作模態頻率，如表3所示。由表3可知，考慮接觸和螺栓預緊力的電機振子有限元模型計算結果與試驗結果基本一致，ANSYS計算的二階彎振頻率（I、II）、一階縱振頻率與試驗結果誤差分別為3．8%、4．4%、4．9%。理想的結果也驗證了我們的接觸問題分析和建立的接觸模型是正確合理的。

表3 基于螺栓聯接有限元模型的工作模態頻率（Hz）Tab.3 The Working Mode Frequency of the Finite Element Model Based on Bolt-Joint（Hz）

5 結論

從實現該種電機的運動和提高其輸出性能的角度出發，首先根據電機結構和工作原理對振子進行動力學設計及確定其結構形式以及壓電陶瓷片在桿式超聲電機振子中的最佳安放位置；其次，在基于螺栓聯接非線性系統的桿式超聲電機精確有限元建模中考慮了接觸和螺栓預緊力，建立了準確反映電機實際結構特性的精確有限元模型。實驗驗證表明，電機輸出性能得到很大改善，對桿式超聲電機設計及動力學分析具有一定的參考價值。

［1］趙淳生．超聲電機技術與應用［M］．北京：科學出版社，2007．（Zhao Chun-sheng．Ultrasonic Motors Technologies and Applications［M］．Beijing：Science Press，2007．）

［2］郭吉豐，白洋，王劍．多自由度超聲波電機的研究進展和展望［J］．振動與沖擊，2013，32（15）：1-7．（Guo Ji-feng，Bai Yang，Wang Jian．Recent development and prospect of multi-degree-of-freedom ultrasonic motors［J］．Journal of Vibration and Shock，2013，32（15）：1-7．）

［3］吳文才．多自由度超聲電機設計與應用研究［D］．南京：南京航空航天大學，2014．（Wu Wen-cai．Research on muliti-degree-of-freedom ultrasonic motor and its application［D］．Nanjing：Nanjing University of Aeronautics and Astronautics，2014．）

［4］徐志科，金龍，胡敏強．一種新型雙定子三自由度超聲波電機特性研究［J］．微電機，2009（4）：27-29．（Xu Zhi-ke，Jin Long，Hu Min-qiang．Research on a novel 3-DOF ultrasonic motor with two cylinder stators［J］．Micromotors，2009（4）：27-29．）

［5］趙淳生，李志榮，劉俊標．圓柱-球體多自由度超聲電機定子的優化設計［J］．壓電與聲光，2004，26（1）：13-16．（Zhao Chun-sheng，Li Zhi-rong，Liu Jun-biao．Optimal design of the stator of the cylinder-sphere ultrasonic motor with multi-degree-of-freedom［J］．Piezoelectrics&Acoustooptics，2004，26（1）：13-16．）

［6］李志榮，趙淳生，黃衛清．圓柱形三自由度超聲電機定子的結構動力學優化設計［J］．振動工程學報，2005，18（4）：471-474．（Li Zhi-rong，Zhao Chun-sheng，Huang Wei-qing．Structural dynamics optimal design of a 3-DOF cylinder type stator of ultrasonic motor［J］．Journal of Vibration Engineering，2005，18（4）：471-474．）

［7］Takemura K，Kojima N，Maeno T．Development of a bar-shaped ultrasonic motor for three degrees-freedom motion［A］．Proceedings of the 4th International Conference on Motion and Vibration Control，1998：195-200．

［8］孫合明．縱扭復合型超聲電機的研究［D］．南京：南京航空航天大學，2000．（Sun He-ming．Research on hybrid ultrasonic motors using longitudinal and torsional vibration modes［D］．Nanjing：Nanjing University of Aeronautics and Astronautics，2000．）

［9］劉俊標．單定子三自由度超聲電機及其控制技術的研究［D］．南京：南京航空航天大學，2001．（Liu Jun-biao．Research on three degree of freedom ultrasonic motor with single stator and its control technology［D］．Nanjing：Nanjing University of Aeronautics and Astronautics，2001．）

［10］鄭宗勇．復雜聯接結構非線性有限元精確建模和模型確認方法研究［D］．南京：南京航空航天大學，2010．（Zheng Zong-yong．Study on nonlinear finite element precise modeling and model validation methods of complex joint structures［D］．Nanjing：Nanjing University of Aeronautics and Astronautics，2010．）