在振動篩上實現振動同步傳動及試驗研究

顧大衛，聞邦椿

（東北大學 機械工程與自動化學院，遼寧 沈陽 110819）

1 引言

在工程技術領域，多激振器的同步理論已經得到廣泛應用，極大促進了社會生產力的發展。1984年，我國學者聞邦椿首次提出了振動同步傳動的概念，他從能量傳遞的角度分析了振動同步傳動的物理過程[1]，文獻[2-5]也對振動同步傳動問題進行了相關的研究。雙激振電機驅動的自同步振動機械通常在兩臺激振電機同時供電的情況下運轉，振動同步傳動理論指出，只要滿足一定的條件，在兩臺電機獲得同步運轉之后，切斷一臺電機的電源，系統仍然可以保持其同步運轉狀態。試驗可以證明，這種單電機供電所需的電力耗能較雙電機供電時節約（15～30）%，而其工藝效果保持不變。

直線振動篩體積小、質量輕、篩孔不易堵塞、容易維護，在礦山及冶金等工業部門得到廣泛應用[6]。根據振動同步傳動原理，只要該類型機械的系統參數滿足一定的條件，在兩臺激振電機獲得同步運轉之后，切斷其中一臺激振電機的電源，兩激振電機仍然可以維持其同步運轉狀態，從而達到節能的目的并且延長了電機的使用壽命。因此，對該類型振動機械的振動同步傳動原理進行研究具有普遍而重要的意義。

2 系統動力學模型的建立

直線振動篩的動力學模型，如圖1所示。包括剛性機體，激振器及彈簧。系統展現x，y和擺動ψ三自由度的振動，激振器1，2分別繞各自旋轉軸反向轉動，以φ1和φ2表示。設oxy為固定坐標，原點o為機體質心平衡點。以x，y，ψ，φ1和φ2為廣義坐標，使用朗格朗日能量方程，同時忽略來自于系統不對稱引起的微量慣性耦合項，可得系統運動微分方程如下：

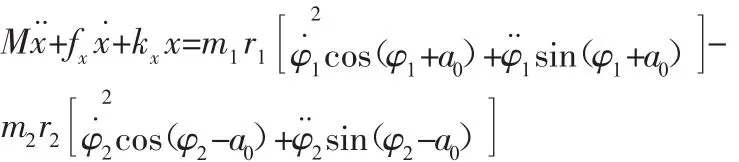
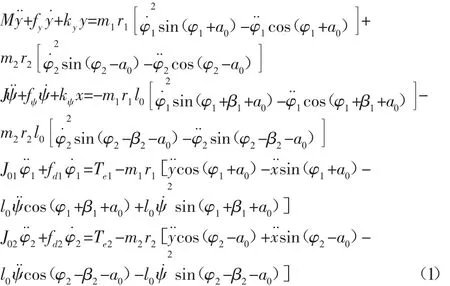
設兩激振器穩態時平均相位及相位差分別為φ和2α，以及m1=m2=m0，r1=r2=r，求得穩態時系統的響應如下：

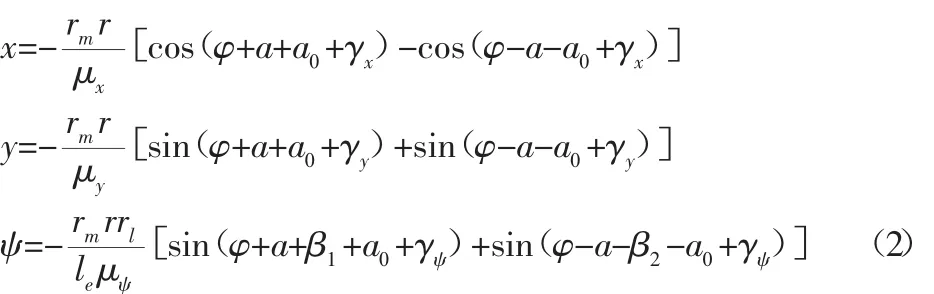
引入 φ1和 φ2瞬時變化系數[7]v1，v2，對式（2）中的 x，y，ψ 在時間 t上求導，將之代入式（1）最后兩個等式中，在 φ=（0～2π）上求積分并且取平均值，得到頻率俘獲方程如下：Av˙=Bv+u （3）

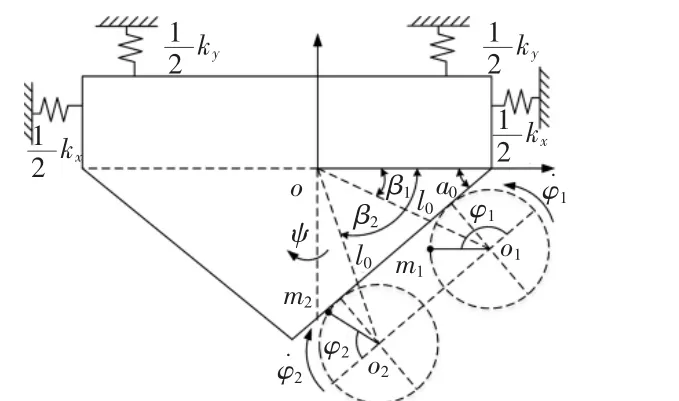
圖1 直線振動篩動力學模型Fig．1 Dynamic Model of the Linear Vibrating Screen

2.1 實現振動同步傳動的同步性判據

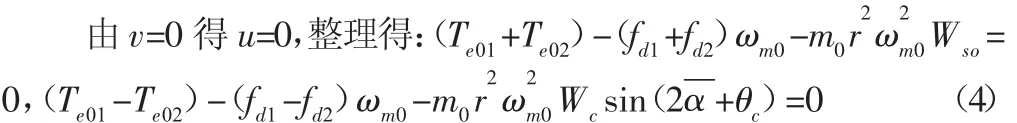
式中：Te01+Te02—兩電機的電磁輸出轉矩之和；（fd1+fd2）ωm0—兩

電機阻力矩之和；m0r2ω2m0Wso—作用在兩電機上的負載力矩之和，因此式（4）第一項稱為振動系統運轉在穩態時總的力矩平衡方程。重新整理式（4）的第二項，得到：

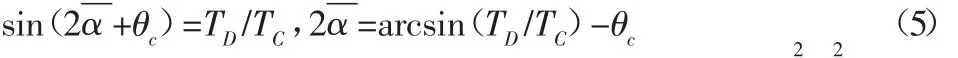
當兩電機處于同步并且系統處于穩態時，切斷電機2的電源，即Te02=0。如果此時兩激振器仍能夠實現同步運轉，則兩激振器將以振動同步傳動的方式運轉。實現系統振動同步傳動的判據為：

2.2 振動同步傳動狀態的穩定性判據

3 試驗驗證

在小型直線振動篩上進行試驗。兩臺一樣反向回轉的感應電機被變頻器控制在供電頻率50Hz下運轉，電機型號VB-326-WB（380V，50Hz，6-pole，Y-連接，額定電流 0．82A，額定轉速950r/min，0．2kW，激振力（0～3）kN），如圖 2 所示。

圖2 型直線振動篩Fig．2 Linear Vibrating Screen

3.1 試驗分析

在開始通電一段時間內，兩電機均以電源供電，由于兩個激振器轉動慣量幾乎相同，因此其角加速度也接近相同。在約10s處時，兩電機的角速度與相位差達到穩定狀態，此時同步轉速n1≈996．1r/min，|2α|≈12．8°，如圖 3 所示。50s時，切斷電機 2 的電源，此時兩激振器原有的同步平衡狀態被打破。在斷電瞬時，電機2的轉速迅速下降，相位差迅速增大，經歷短暫的波動，兩激振器穩定在另一平衡狀態下，即振動同步傳動狀態。此時，振動同步傳動狀態下的同步轉速n2≈988．2r/min°，在振動同步傳動過程中，頻率俘獲力矩TC把來自于電機1的驅動力矩傳遞給斷電的電機2以克服電機2的負載力矩。在開始供電的一段時間內，當系統通過共振區時激起x，y，ψ方向的共振響應。在約10s處，響應達到穩定狀態，系統主要運動形式為x方向和y方向振幅近似的直線運動。在50s處，電機2斷電，響應發生細微波動，隨后迅速恢復穩定狀態。系統的主要運動形式仍為x方向和y方向振幅近似的直線運動，這種運動形式為工程所需要，如圖4所示。

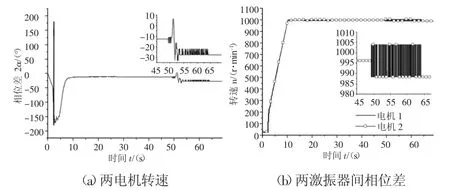
圖3 兩電機轉速及激振器間相位差Fig．3 The Rotate Speed and Phase Difference of Two Exciters

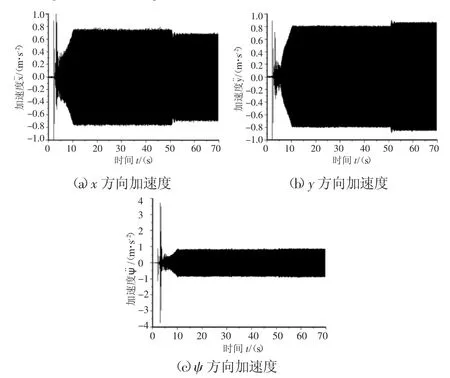
圖4 系統各方向的運動加速度Fig．4 The Acceleration Curves of the Vibrating System

3.2 高速攝影儀記錄

供電頻率50Hz下高速攝影機記錄的電機2斷電前后穩態時的回轉相位，以回轉中心連線為基準線，相位誤差在（0～1）°，如圖5、圖6所示。在圖5中，電機2斷電前穩態時相位差為（11．0～13．1）°。在圖 6 中，電機 2 斷電后穩態時相位差為（27．1～28．3）°。此結果與圖3（b）基本一致。

圖5 電機2斷電前穩態時的兩激振器相位Fig．5 Phase of Two Exciters in the Steady State Before Motor 2 is Cut off

圖6 電機2斷電后穩態時的兩激振器相位Fig．6 Phase of Two Exciters in the Steady State After Motor 2 is Cut off

3.3 系統參數代入理論結果的驗證

試驗中的直線振動篩結構參數為：M=160kg，m1=m2=m0=4kg，J=18．12kg·m2，le=0．34m，kx=96kN/m，ky=77kN/m，kψ=15kN/rad，fx=fy=0．3kN·s/m，fψ=0．2kN·s/rad，fd1=fd2=0．003kN·s/rad，ξnx=ξny=ξnψ=0．07，a0=40°，l0=0．29m，β1+β2=π/2，r=0．05m。將試驗系統結構參數代入穩定性判據式（13）中，如表1所示。可知振動同步狀態下的穩定性指數都大于零，說明系統穩定，這也驗證了所用理論方法的有效性。

表1 電機二斷電后系統振動同步傳動狀態下的穩定性Tab.1 Stability on Vibratory Synchronization Transmission After Motor 2 is Cut off

4 結論

（1）對于直線振動篩動力學模型，要想實現振動同步傳動，首先必須實現雙機同時供電下的同步運轉，產生頻率俘獲力矩，以保證系統在振動同步傳動過程中進行扭矩傳遞。（2）電機2斷電前穩態時的同步轉速為 n1≈996．1r/min，相位差|2α|≈12．8°。電機2斷電后穩態時（振動同步傳動狀態）的同步轉速為n2≈988．2r/min，相位差|2α|≈27．7°，與斷電前相比，同步轉速下降，相位差增加。（3）由于同步轉速和相位差變化不大，電機2斷電前后穩態時系統的主要運動形式保持不變，即直線振動篩在振動同步傳動狀態下也能維持正常工作。

［1］聞邦椿，林向陽．振動同步傳動及工業應用［J］．機械工程學報，1984，20（3）：26-43．（Wen Bang-chun，Lin Xiang-yang．Vibratory synchronization transmission and its industry applications［J］．Journal of Mechanical Engineering，1984，20（3）：26-43．）

［2］聞邦椿，趙春雨．機械系統的振動同步與控制同步［M］．北京：科學出版社，2003．（Wen Bang-chun，Zhao Chun-yu．Vibratory Synchronization and Controlled Synchronization in Mechanical System［M］．Beijing：Science Press，2003．）

［3］Wen Bang-chun，Fan Jian，Zhao Chun-yu．Vibratory Synchronization and Controlled Synchronization in Engineering［M］．Beijing：Science Press，2009．

［4］Zhao Chun-yu，Zhu Hong-tao，Wang Rui-zi．Synchronization of two nonidentical coupled exciters in a non-resonant vibrating system of linear motion，part I：Theoretical analysis［J］．Shock and Vibration，2009（16）：505-515．

［5］Zhang Xue-liang，Zhao Chun-yu．Theoretical and experimental study on synchronization of the two homodromy exciters in a non-resonant vibrating system［J］．Shock and Vibration，2013（20）：327-340．

［6］彭利平，劉初升，趙躍民．混聯彈簧減振系統下自同步直線振動篩的動力學特性［J］．煤炭學報，2014（10）：2114-2120．（Peng Li-ping，Liu Chu-sheng，Zhao Yue-min．Dynamic characteristics of a self-synchronous linear vibrating screen with hybrid-spring isolators［J］．Journal of China Coal Society，2014（10）：2114-2120．）

［7］梁迪，趙春雨．振動系統機電耦合研究的現狀與展望［J］．機械設計與制造，2005（2）：99-103．（Liang Di，Zhao Chun-yu．State and prospect in studies on electromechanical coupling of vibration system［J］．Machinery Design&Manufacture，2005（2）：99-103）．