基于DEPSO-NIW算法的電源規劃算法

張文哲

（重慶市電力公司交易中心，重慶404100）

0 引言

電源規劃的目的是以某一時期的負荷預測為根據，在滿足一定可靠性的前提下找到一種最經濟的電源開發方案，用以確定何時、何地投入和建設何種規模、何種類型的發電機組[1]。電源規劃問題是一種非凸的、高維數、非線性的、離散的優化問題,理論上很難找到最優解。因此，本文結合電源規劃問題的復雜性和特殊性，提出了一種基于差分進化算法的非線性動態慣性權重的粒子群算法（DEPSO-NIW）。

1 國內外研究現狀

目前，國內外的電源規劃算法，主要有三大類，分別是啟發式算法、數學規劃算法和智能優化算法。其中，啟發式算法依靠實際經驗或者直觀判斷進行尋優,不具備晚上的理論依據，其主要包括優先順序法、局部尋優法等；數學規劃算法具有嚴格的理論依據,可以保證理論上的全局最優解,但求解條件苛刻,計算量大,實際中難以操作，主要包含線性規劃法（LP）[2]、混合整數規劃法（MIP）[3]、動態規劃法[4]等；智能優化算法屬于隨機算法,模仿自然界中各種現象,具有高度的靈活性,對問題無嚴格要求,但部分算法的理論基礎相對薄弱,不易獲取全局最優解，主要包括專家系統[5]、模糊理論[6]、遺傳算法（GE）[7]、粒子群算法（PSO）[8]、模擬退火算法、混沌算法等。

2 基于差分進化算法的非線性動態慣性權重的粒子群算法（DEPSO-NIW）

2.1 標準粒子群算法

假定一個粒子數為M的群體以某一速度在一個D維搜索空間內飛行。粒子i在t時刻的狀態屬性設置如下式（其中，1≤d≤D，1≤i≤M）：

（1）位置

（2）速度

（3）個體最優位置

（4）全局最優位置

（5）t+1時刻PSO粒子的速度更新公式

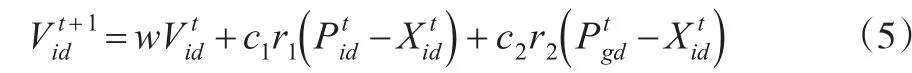
（6）t+1時刻PSO的位置更新公式

式（5）主要由三部分組成：第一部分代表粒子對之前的速度的繼承，表示粒子對當前本身運動狀態的信任程度，根據粒子自身的速度來進行慣性運動；第二部分為“認知”部分，它象征了粒子對自身的思考，即通過對自身之前的經歷進行綜合分析從而確定下一步的行為決策。這種行為決策即為“認知”，它反映了一個增強學習的過程；第三部分為“社會”部分，代表粒子個體之間的的信息共享和相互協作。在搜索過程中，粒子一方面記住它們自己本身的經驗，與此同時還考慮其他粒子的經驗。當單個粒子發覺其他同伴有較好的經驗時，它會改變適應性以尋求統一的認知過程。

PSO算法在優化前期具有較快的收斂速度，在優化后期易陷入局部最優的狀態。這是由于在初期的優化過程中，整個種群的保持著較高多樣性，這時的適應度值變化較大，表現為快速收斂的局部最優。隨著群體中的粒子逐步向最優粒子靠近，整個群體的多樣性會維持在較小的范圍內，其表現為適應度值變化緩慢或保持不變，此時，PSO算法出現了停止現象，即早熟現象。

2.2 非線性動態慣性權重

在PSO算法中，慣性權重w決定了粒子當前飛行速度受先前飛行素的的影響程度。當w較大時，局部搜索能力弱，全局搜索能力強，盡管收斂速度較快，但不容易找到精確解；當w較小時，局部搜索能力強，全局搜索能力弱，較容易找到精確解，但收斂速度較慢，且可能陷入局部最優的狀態。

慣性權重的取值策略主要包含線性和非線性策略。線性策略由于具有線性遞減的特征，算法在迭代過程中一旦進入局部極值點附近，就會很難跳出，為克服這一缺陷，解決PSO算法使用過程中慣性權重選擇的費時且低效的問題，本文擬采用非線性動態慣性權重的粒子群算法（PSO-NIW）。

在全局優化算法中，最好的情況就是在前期具有較高的全局搜索能力，然而在后期具有較高的開發能力，以便前期可以更好地找到合適的種子。后期可以提高收斂速度，因此慣性權重w的值應該是呈遞減趨勢的。PSO-NIW算法的慣性權重表達式為：

式（7）中，w(t)為在第t次迭代過程中的慣性權重值；wstart為慣性權重初始值，也是最大值;wend為迭代過程結束時的慣性權重值,也是最小值；tmax為最大迭代次數;k為控制因子，用于控制w隨t變化曲線的平滑度（實驗數據顯示：k=0.5時為遞減凸函數，k=1.5時近似線性遞減函數，k=5時為先凸后凹的遞減函數，k=10時近似遞減凹函數）。因此，PSO-NIW算法的位置方程式不變：

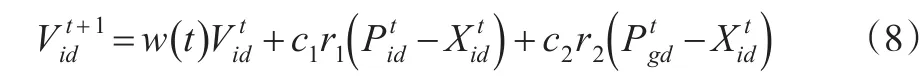
2.3 差分進化算法（DE）

假設對于一個最小化問題minf(x)，DE從包含M個候選解的初始種群開始，i=1,2,…,N，其中i為種群數，t為當前代。

（1）變異操作

DE算法最基本的變異成分為父代的差分矢量，對于父代（第t代）種群中的任意兩個不同的個體，其差分矢量定義為：

將差分矢量與另外一個隨機的個體相加，即為變異矢量。對于目標矢量x，其變異操作為：

其中，r1,r2,r3∈[1,2…,i-1,i+1,N]，F∈(0,2)。r1、r2、r3為隨機數;F為加權因子。

（2）交叉操作

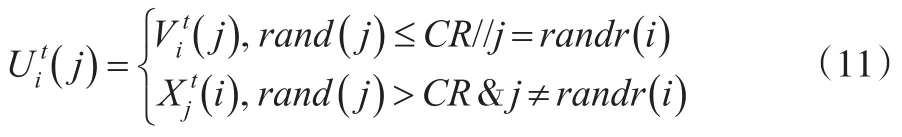
式（11）中，j為第j個變量（基因）；rand(j)為[0,1]內均勻分布的隨機數；CR為變異概率，CR∈[0,1];randr(i)為隨機選擇指數，randr(i∈[1,2,…,D])

（3）選擇操作

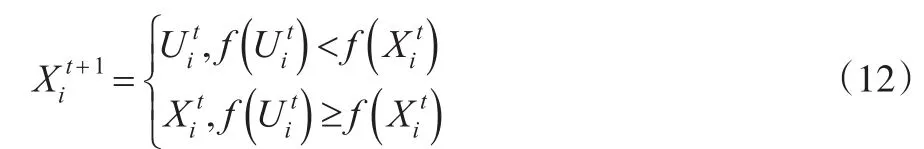
式（12）中，f(x)代表適應度函數。

DE算法在選擇操作的過程中采用了一種“貪婪”搜索的策略，即經歷了變異及交叉操作后的個體與父代個體競爭，若其適應度好于父代，才會被選作子代，若其適應度比父代差，則直接進入下一代。該算法可以增加算法的收斂速度，但也容易陷入局部最優點而使算法停滯。

2.4 基于差分進化算法的非線性動態慣性權重的粒子群算法（DEPSO-NIW）

針對單一的PSO和DE算法易陷入局部最優的缺陷，本文將PSO算法與DE算法相結合，即基于差分進化的粒子群算法（DEPSO）。

DEPSO算法的本質思想是通過引入了一種新的信息交流機制，使信息能夠在兩個種群中傳遞，有利于個體避免錯誤的信息判斷從而陷入局部最優。

為了進一步提高DEPSO算法的優化性能，本文采用上文中提出的非線性動態慣性權重策略，提出了一種基于差分進化算法的非線性動態慣性權重的粒子群算法（DEPSO-NIW），用以求解電源規劃模型。

DEPSO-NIW算法的基本流程圖如圖1所示。

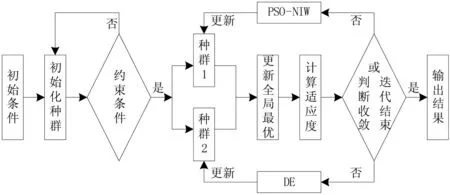
圖1 DEPSO-NIW算法流程圖

3 算例與結果

本文分別用傳統的粒子群算法（PSO）和本文所提出的基于差分進化的非線性動態慣性權重粒子群算法（DEPSO-NIW）對某地區2011—2020年的電源規劃模型進行最優求解，編程軟件為MATLAB。

DEPSO-NIW算法各個參數設置如表1所示。

表1 DDEPSO-NIW算法參數設置

兩種算法的全局最優點運動過程如圖2所示。

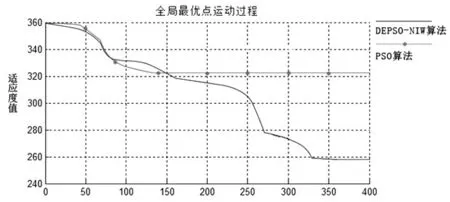
圖2 DEPSO-NIW與PSO算法全局最優點運動過程

由圖2可以看出，傳統的PSO算法很快就進入了局部最優，而DEPSO-NIW算法可以使粒子從局部最優中跳出來，擴大了搜索面積。結果顯示DEPSO-NIW算法能夠得到更好的適應度值。

4 結論

本文通過對國內外現有的電源規劃算法進行比較研究，并結合電源規劃的特性，將粒子群算法（PSO）與差分進化算法(DE)相接和，并引入非線性動態慣性權重（NIW）,提出了一種基于DEPSO-NIW算法的電源規劃研究。通過分析比較和實際算例，證明了此算法具有較好的全局搜索能力和優化性能。

[1]王錫凡.電力系統規劃基礎[M].北京:中國電力出版社,1994.

[2]梁宇希,黃國和,林千果等.基于不確定條件下的北京電源規劃優化模型[J].電力系統保護與控制，2010,38(15).

[3]孔祥玉,房大中.不確定多目標電源規劃模型[J].天津大學學報,2008,41(2).

[4]周景宏,胡兆光,田建偉,肖瀟.電力綜合資源戰略規劃模型與應用[J].電力系統自動化,2010,34(11).

[5]耿建,徐帆,姚建國等.求解安全約束機組組合問題的混合整數規劃算法性能分析[J].電力系統自動化，2009,33(21).

[6]王楠,張粒子,謝國輝.求解機組組合問題的改進混合整數二次規劃算法[J].電力系統自動化,2010,34(15).

[7]丁明,石雪梅.基于遺傳算法的電力市場環境下電源規劃的研究[J].中國電機工程學報,2006,26(21).

[8]Pang C K,Chen H C.Optimal Short-Term Thermal Unit Commitment[J].IEEE Trans on PAS,1976,95(4).