收益共享下的雙渠道庫存與運輸動態聯合優化研究

胡曉輝，胡安建，薛婉璐，李富昌

（云南師范大學經濟與管理學院，昆明650500）

0 引言

隨著電子商務的發展及網絡技術的應用，網絡直銷渠道得到迅速發展。越來越多制造商在保留傳統零售渠道的同時，紛紛開拓新型網絡直銷渠道，實現與消費者直接溝通和交互，這種將網絡直銷渠道與傳統零售渠道相結合的雙渠道模式已成為當今制造企業的一大特色。然而，網絡直銷渠道的發展勢必對傳統零售渠道商的產品定價、市場份額和利潤構成威脅，因此，能否有效化解這種雙渠道之間的利益沖突，成為制造商必須面對并妥善解決的現實問題。庫存與運輸作為參與方主要業務，是雙渠道協調的核心問題。因此，研究雙渠道庫存與運輸聯合優化問題對于制造商有效實施雙渠道策略具有重要的理論價值和現實意義。收益共享契約是指制造商以較低的價格向下游企業提供商品，下游企業為了彌補制造商因降價造成的損失而約定將銷售收入的一部分返還給制造商的一種契約。本文從雙渠道供應鏈視角出發，構造一種新的收益共享契約，設置參與方之間的利潤出讓參數，以尋求雙渠道供應鏈利益協調和庫存與運輸的聯合優化。

1 問題描述與模型假定

本文研究的雙渠道供應鏈庫存與運輸協調優化問題的假設如下：①雙渠道供應鏈由一個制造商、一個線下零售商（即傳統的零售商）和一個線上零售商（即網店銷售）組成，即制造商—線下零售商，制造商—線上零售商兩種渠道；②該制造商直接為線上線下零售商內部供貨，按照零售商的市場需求份額配送，故線上線下零售商庫存成本為零；③雙渠道供應鏈各參與方都是風險中立和完全理性的，即制造商、線下線上零售商都是理性“經濟人”，將依據各自的利潤最大化條件進行決策；④在制造商—線上零售商銷售渠道中，制造商占據主導地位，始終控制著價格水平，例如阿迪達斯正品在網店的價格與專賣店的價格幾乎一致，由廠家控制價格；而在制造商—線下零售商銷售渠道中，制造商和線下零售商的地位則由市場供求關系決定。

在雙渠道供應鏈中，制造商為線下和線上零售商配送成本為C的商品，C包含生產成本和運輸成本，在線下銷售渠道中，傳統零售商以p1的價格銷售產品給消費者，而在線上銷售渠道中，網店零售商以p2的價格進行銷售。市場需求D與價格p存在線性相關關系，且與零售商的努力程度有關，故本文設計線性函數來研究它們之間的相關關系。令Φ=D(p1,p2)，Ω=kiyi，其中i取1和2。在制造商—線下零售商供應鏈中，線下零售商所面臨的需求函數為F1(Φ,Ω)=γm+n2p2+k1y1-n1p1-k2y2，其中，m為市場需求總額，γ(0＜γ≤1)為雙渠道下制造商—線下零售商銷售渠道消費者需求的市場份額，n1（n1＞0）為雙渠道下，線下零售商的市場需求量對銷售價格的敏感度系數，k1為線下零售商的市場需求量對其努力水平y1的敏感度系數，n2（0＜n2＜n1）表示兩種渠道之間因價格的變化而引起的需求擴散程度，k2表示線下零售商的市場需求量對線上零售商努力程度y2的敏感度系數；在制造商—線上零售商供應鏈中，線上零售商所面臨的需求函數為F2(Φ,Ω)=(1-γ)m+n2p1+k2y2-n1p2-k1y1，k2為市場需求量對線上零售商促銷努力水平y2的敏感度系數，k1表示線上零售商的市場需求量對線下零售商努力程度y1的敏感度系數。制造商的單位產品庫存成本為c1，線下零售商的努力成本函數為G(y1)=μ1，線上零售商的努力成本函數為G(y2)=μ2，其中μ1、μ2表示相應的努力成本對其努力程度的敏感度系數，且都大于0。

2 收益共享下的雙渠道庫存與運輸動態聯合優化

在VMI模式下的雙渠道供應鏈中，制造商有線下零售商和線上零售商兩條銷售渠道，并且制造商是這兩條銷售渠道中庫存水平D和產品價格p的決策者。依據經濟人假設，本文研究目的是在利潤最大化水平下，尋求線下零售商和線上零售商的最佳努力水平Y，以此達到兩系統同時決策時整體效率水平最優。因此，本文只考慮以下三種博弈模式，即雙方同時決策的靜態Nash博弈，線下零售商優先決策的Stackelberg博弈和線上零售商優先決策的Stackelberg博弈，另外，為了有效的進行收益分配，設計了基于收益共享契約的雙渠道供應鏈庫存與運輸動態收益協調模型，并進行求解。

2.1 雙渠道供應系統中雙方同時決策的Nash靜態博弈

模式一：雙方同時決策的Nash靜態博弈。在此情形下，本文認為線下零售商和線上零售商具有水平一致的渠道能力，此時零售商之間表現出程度較高的競爭關系。線下零售商和線上零售商通過n階段討價還價來決定供應鏈的庫存水平和努力水平。此時，線下零售商系統和線上零售商系統的利潤函數分別為：

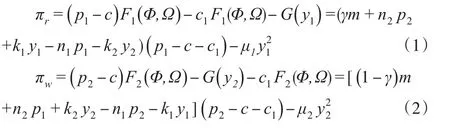
在以上兩個利潤函數中，價格既定的情況下，制造商要在兩條渠道中分別取得最大收益，需要求出兩個利潤函數的最大值。此時，式（1）和式（2）的決策變量yi需滿足二階導數因此可以求出努力程度yi。在求出的努力程度yi的基礎上，再尋求制造商在兩個銷售渠道中所能獲得的最大利潤，需求出兩個利潤函數的最大值，此時，式(1)和式(2)的決策變量pi需滿足二階導數因此可以求出最優價格水平pi。為求出兩個銷售渠道各自最優努力程度和最優價格水平，對式（1）和式（2）分別求關于yi和pi的一階導數并令其等于零，解得：

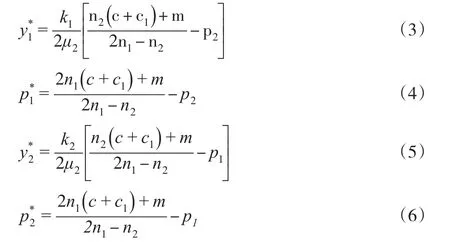
2.2 雙渠道供應系統中一方優先決策的Stackelberg博弈

模式二：線下零售商優先決策的Stackelberg博弈。在Stackelberg博弈情形下，本文認為制造商具有較強的渠道能力。在制造商—線下零售商銷售渠道中，第1階段，制造商督促線下零售商率先確定其努力水平；第2階段，在該努力水平被確定之前，線下零售商將會考慮網絡銷售系統中線上零售商可能做出的反應；第3階段，線下零售商依據上一階段作出判斷，確定其努力水平；第4階段，線上零售商依據線下零售商在第3階段作出的決定，確定其努力水平。至此結束，制造商可確定其在兩個渠道中的最優庫存量及最優定價。

由模式二可知，線上零售商依據線下零售商的決策來確定其最優努力水平和最佳定價，因此對式（2）求關于p2和y2的一階偏導并令其等于零求得。因此，網絡銷售系統的最優售價和最佳促銷水平由式（2）的關于函數πw對p2和y2的一階偏導等于零求得，即為：

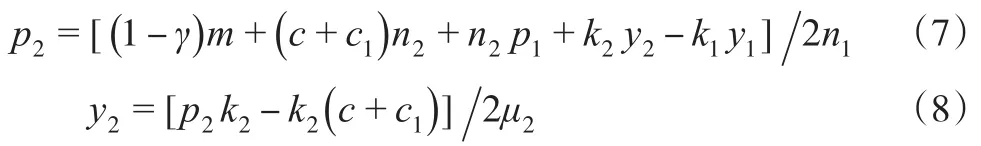
將式（8）和式（4）代入式（7）中可得：

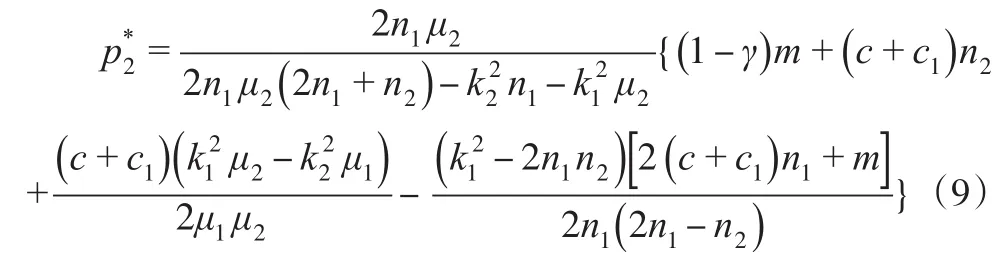
再將式（9）代入式（8）中可解得：

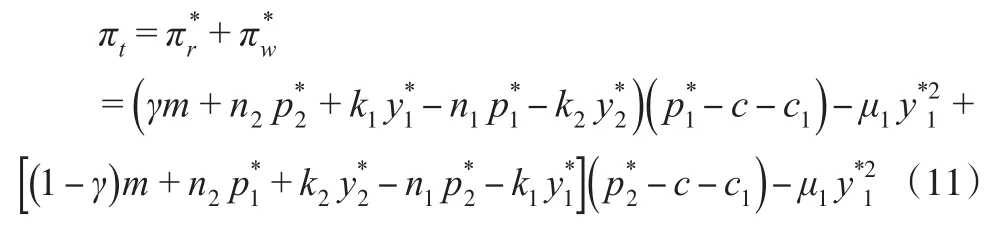
模式三：由模式二同理可得，線上零售商優先決策的Stackelberg博弈中，制造商會更多的傾向于網絡銷售，因此，線下零售商依據線上零售商的決策來制定決策。此時，求出制造商在線下銷售渠道的最優售價和最佳促銷水平，對式（1）關于pi和yi求一階偏導并令其等于零，可得：

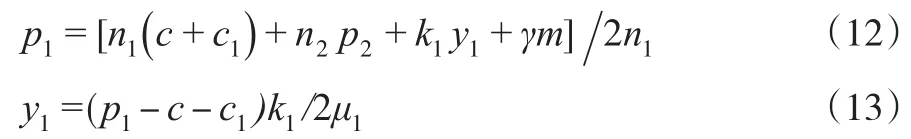
將式（6）和式（13）代入式（12）中，可得：

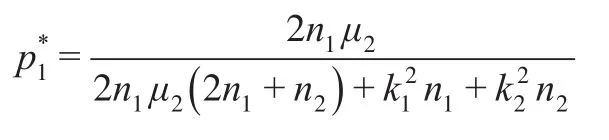
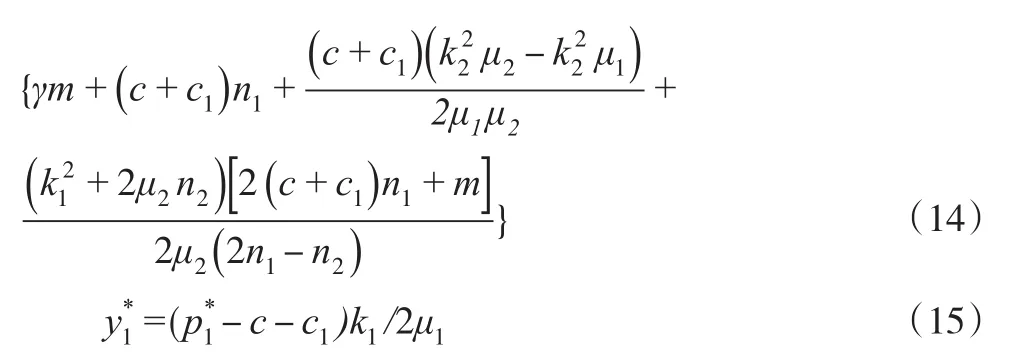
綜上所述，雙渠道供應鏈中共同決策下的最優定價和最佳努力水平均大于分別優先決策下的最優定價和最佳努力水平，即雙渠道供應鏈收益協調沒有實現。因此，下文引入收益共享契約進行收益協調。

2.3 基于收益共享契約的雙渠道供應鏈庫存與運輸動態收益協調模型

庫存與運輸成本占供應鏈成本的很大一部分，因此對于庫存與運輸進行聯合優化以節約成本非常必要。本文的庫存與運輸聯合優化是指線上零售商和線下零售商從雙渠道供應鏈整體出發，將庫存與運輸成本聯合考慮以實現整體收益最優。集中決策時，制造商的總利潤函數表示為：

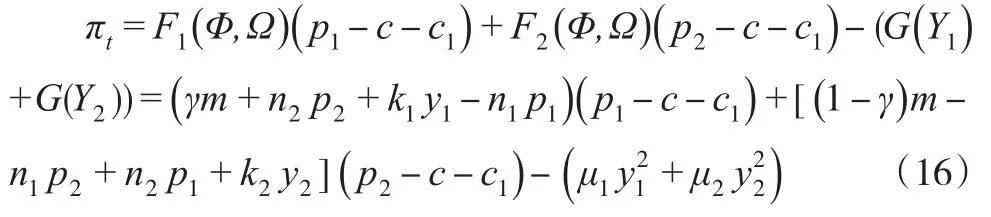
該利潤函數是關于線下零售商和線上零售商的二元凹函數，為使庫存與運輸聯合優化（ITIO）以后整體利潤最大，需對式（16）關于pi和yi分別求一階、二階及混合偏導，且滿足，其中對式（16）中的pi和yi分別求一階偏導并令其為等于零，解得：

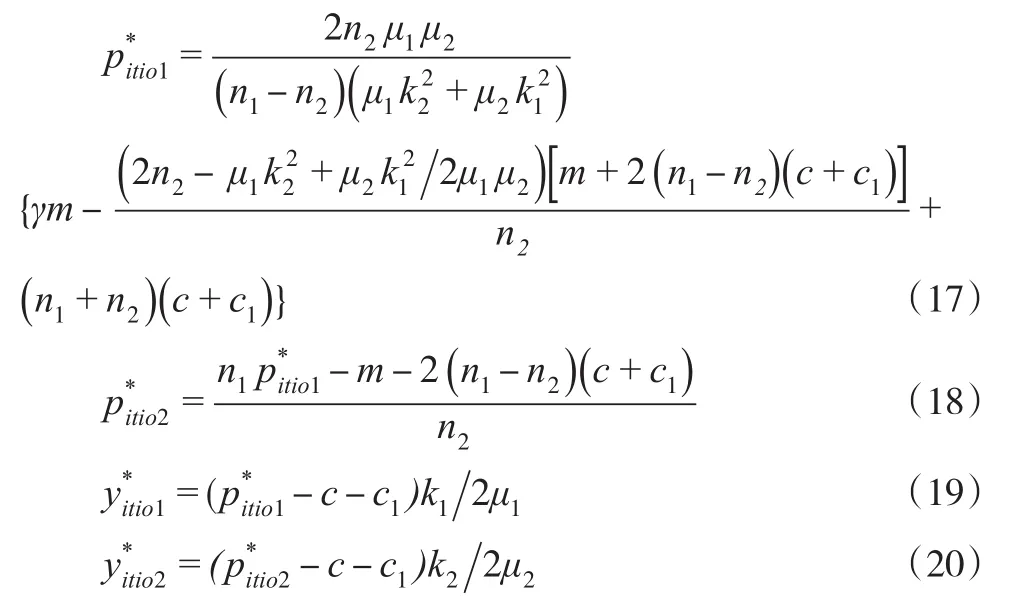
記πitio1、πitio2分別是和時，制造商在線下銷售渠道和線上銷售渠道所獲得的利潤，即：

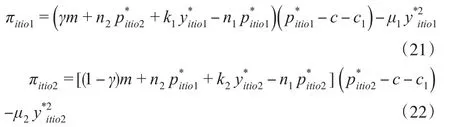
制造商在傳統銷售的基礎上開拓網絡市場，為了減輕兩種渠道之間的沖突，需要建立一種激勵機制，以激勵線下零售商與其合作。該激勵機制將制造商在兩種渠道中所得到的利潤進行協調，一般分為三種情形。情形一：線下零售商的收益會增加，線上零售商的收益會減少，即πitio1＞πr且πitio2＜πw，此時線下零售商為線上零售商提供這樣一個收益共享契約，該契約使制造商在線下銷售渠道中收益增加的一定份額轉移給線上零售商，使得線上零售商的收益在庫存與運輸聯合優化之后大于單獨決策時的收益，該契約保證了參與者之間合作的順利進行。依據假設②可知，在該情形下制造商將提高線下銷售渠道的庫存量，即St1＞St2＞0且St=St1+St2。情形二：與情形一情況相反，線上零售商的收益增加，線下零售商的收益減少，即πitio2＞πw且πitio1＜πr，此時制造商會增加網絡直銷渠道的產品庫存量，即St2＞St1＞0且St=St1+St2；情形三：雙方的利潤都會增加，因為一般兩方的利潤增加和減少是此消彼長的，該情形一般不會發生，并且由于情形一和情形二的情況分析類似，因此，本文只對情形一進行研究。

在情形一發生的情況下，線下零售商給線上零售商提供收益共享契約，將其在庫存與運輸聯合優化時所實現利潤πitio1的θ倍轉移給線上零售商，并記此時線下零售商和線上零售商的利潤分別為，由以上表述可知：

由式（24）至式（27）可知：

將式（1）、式（2）、式（21）和式（22）代入式（27）中可得：

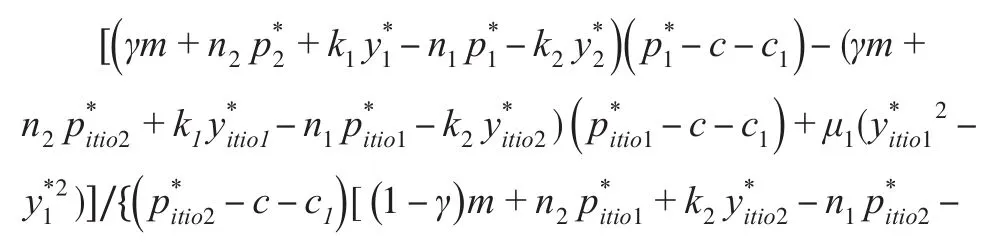
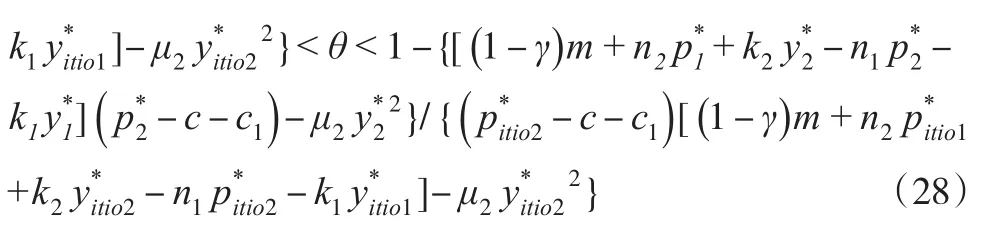
由式（28）可知，在收益共享契約中，各契約參數之間相互影響，相互制約。依據理性人假設，渠道中各參與者的目標是實現自身收益最大化，即滿足自身利益最大的前提下，配合實現整體利益最優。為了能使該契約順利進行，參與方之間相互協作，只要分享份額θ滿足式（28）的范圍，線下線上零售商的合作就能順利進行，即可保證在既調節了收益分配的條件下，雙渠道中各參與方也能達到帕累托改進，制造商在和時達到最佳庫存量，實現庫存與運輸的聯合優化。

通過對以上線下零售商和線上零售商的不同博弈情形分析，本文可以得出以下命題結論：

命題1：在雙方同時決策的Nash靜態博弈中

（a）線下零售商的最優策略：

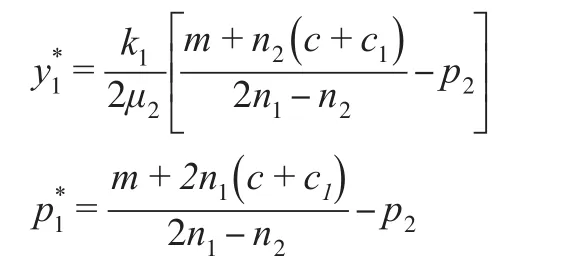
（a）部分表明，在Nash靜態博弈中，兩條渠道存在最優策略，制造商可得到最大利潤；（b）部分表明，隨著市場需求總額的增加，相應的銷售價格和努力水平也會增加，努力水平隨著市場需求量對于零售商努力水平敏感度的增大而增大，隨著零售商努力成本對其努力程度的敏感度的增加而減小。在線上銷售渠道中，線上零售商也會面臨同樣的策略選擇，從而實現自身利潤最大化。因此，在模式一中，雙方應充分考慮競爭對手可能的決策，遵從市場競爭機制，以避免造成資源的浪費，達到帕累托最優。

命題2：在一方優先決策的Stackelberg博弈中

（a）線下零售商優先決策時，線上零售商的最優策略：

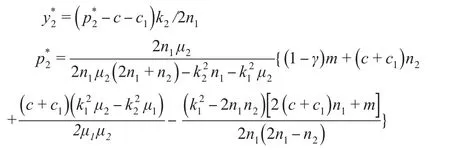
（a）部分表明，在Stackelberg博弈中，無論哪方優先決策，另外一方總能找到自己的最優策略，即最優策略是存在的；（b）部分表明，在線下零售商優先決策時，線上零售商可以根據市場的需求變化來制定自己的最優定價和努力水平。但從敏感度分析來看，線下銷售渠道中消費者需求的市場份額對線上零售商的市場定價具有反向的制約作用，使得線上零售商的定價低于各自決策時的價格策略水平，弱化了線上零售商的收益水平。并且，定價越高，市場需求量對線上零售商努力水平敏感度系數越大，線上零售商越努力。因此，須對兩條渠道的收益進行有效的分配協調，以此來實現制造商在雙渠道中的整體收益最大化。

命題3：在基于收益共享契約的雙渠道供應鏈庫存與運輸動態收益協調模型中

（a）在制造商集中決策時，兩系統的最優策略：

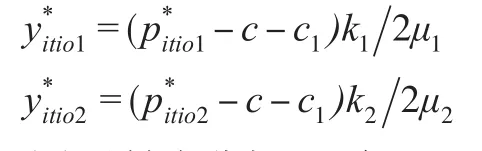
（b）靈敏度分析：πt與ni、ki呈現正向相關，與μi呈現負向相關。

（c）雙渠道供應鏈中，線上零售商和線下零售商之間存在可行的收益共享契約參數。

（a）部分表明，在雙渠道供應鏈制造商集中決策時，存在最優策略，使得雙方的利潤達到最大化，達到帕累托最優；（b）部分表明，在該決策模型中，總體利潤隨著市場的價格敏感系數和努力水平敏感系數的增大而增大，隨著努力成本對努力程度的敏感度系數的增大而降低；（c）部分表明，為了保證雙渠道中參與方合作順利進行且降低不必要的成本，線下零售商和線上零售商之間存在利益協作的可能性，即只要滿足契約參數的范圍，在契約參數不等式中，契約參數θ隨著線下銷售渠道份額γ的增大而增大，即線下銷售渠道所占的份額越大，其聯合優化之后的利潤所需轉移給線上零售商的份額也就越多。因此可調節市場需求份額γ來選擇合適的收益共享契約參數θ，使得供應鏈整體、線下零售商和線上零售商的收益相比分散決策時都有所增加，實現雙渠道整體優化目標。

3 結論

本文在需求價格彈性條件下，通過構建需求函數和收益函數，比較了線下零售商和線上零售商在Nash靜態博弈模型、Stackelberg博弈模型和集中決策模型中個體利潤、總利潤和最佳庫存量。研究結果表明：在集中決策模型中，線下零售商和線上零售商的聯合收益達到最大化，且各自的庫存量及運輸成本都得到了優化；必須指出的是雙渠道供應鏈總體利潤最大化和產品庫存量最優化這一目標的實現，是以收益共享契約的存在為前提的，即獲得較大收益的一方必須承諾將超出預期收益的θ倍返還給另一方；通過構建庫存與運輸聯合優化時各決策主體的收益分配模型，并結合雙渠道特點，設計的收益共享契約協調模型，能夠實現雙渠道供應鏈的協調，并給出了雙渠道供應鏈達到協調時，契約參數的取值范圍的表達式；按照契約參數的分配，最終使得線下零售商和線上零售商的利潤都會增加。本文的收益共享契約是在需求確定和信息對稱的條件下設立的，需求不確定和信息不對稱條件下基于收益共享契約的雙渠道供應鏈庫存與運輸聯合優化是未來值得研究的方向。

[1]Yao D Q,Liu J J.Competitive Pricing of Mixed Retail and Etaild Istrebutionchannels[J].Omega,2005,33(3).

[2]Kurata H,Yao D Q,Liu J J.Pricing Polices Under Directvs.Indirect Channel Competition and Nationalvs.Store Brand Competition[J].European Journal of Operational Reseach,2007,180(1).

[3]Cai G,Zhang Z G,Zhang M.Game Theoretical Perspectives on Dual-channel Supplycha-income Petition With Price Discount Sand Pricingschemes[J].International Journal of Production Economics,2009,117(1).

[4]DeCroix G A,Ha A Y.Optimal Shared-savings Contracts in Supply chaIns:Linear Contracts and Double Moral Hazard[J].European Journal of Operational Research,2005,163(3).

[5]Bertazzi L,Paletta G,Grazia S M.Deterministic Order up to Level Policies in an Inventory Routing Problem[J].Transportation Science,2002,36(11).

[6]Chen C T.A Coordinated Approach to Hedge the Risks in Stochastic Inventory-routing Problem[J].Computers＆Industrial Engineering,2009,56(3).

[7]晏妮娜,黃小原,劉兵.電子市場環境中供應鏈雙源渠道主從對策模型[J].中國管理學,2007,15(3).

[8]曲道鋼,郭亞軍.分銷商需求與其努力相關時混合渠道供應鏈協調研究[J].中國管理科學,2008,16(3).

[9]徐廣業,但斌,肖劍.基于改進收益共享契約的雙渠道供應鏈協調研究[J].中國管理科學,2010,12(6).

[10]孫彩虹,田真真,于輝.零售商退出風險的供應鏈沖擊與協調契約分析[J].中國管理科學,2016,24(6).

[11]但斌,吳慶,張旭梅,肖劍.第三方物流提供商與客戶企業的共享節約合同[J].系統管理理論與實踐,2007,(2).

[12]王勇,孫海雷,陳曉旭.基于數量折扣的改良品供應鏈協調策略[J].中國管理科學,2014,22(4).

[13]李富昌.庫存與運輸協調優化利潤分配研究[J].工業技術經濟,2012,(11).

[14]肖繼先,康玉茜,孔閃閃.最大最小運送周期下的庫存與運輸優化模型[J].遼寧工程技術大學學報：自然科學版,2013,32(3).

[15]葛顯龍,辜羽潔,王偉鑫.供應鏈環境下的庫存與運輸整合優化模型及算法[J].系統工程,2014,32(1).

[16]盧亞秀.VMI模式下天然氣供應鏈的庫存與運輸協調優化研究——以川渝地區為例[D].成都：成都理工大學碩士論文,2015(5).

[17]馬小勇,陳良華.考慮零售商庫存轉運的兩級供應鏈回購契約協調機制研究[J].統計與決策,2017,(2).