數控插床無沖擊讓刀機構的凸輪輪廓線設計與計算
李 欣 張靜雙 徐 慧
(天津機電職業技術學院,天津 300350)
機床振動是影響機床加工精度和機床穩定性的關鍵因素,考慮機床大型零件的動靜剛度、機床往復運動與回轉運動的頻率,進而確定機床的動、靜剛度指標,是機床設計的關鍵環節。數控插床的主軸往復運動和讓刀運動是其規則振動的主要驅動源,改善讓刀運動的運動狀態和減小由于讓刀運動帶來的沖擊,是讓刀機構設計的一個關鍵。目前為了適應更復雜的機床應用環境,通過優化凸輪曲線,設計不具有剛性沖擊甚至不具有柔性沖擊的雙共軛凸輪讓刀機構迫在眉睫。
數控插床由液壓缸對刀軸進行驅動提供往復插削運動,可以進行正常的等速上下往復運動。由于液壓缸活塞桿的影響使得油缸上下油腔面積不等,可以利用這一特性,改變刀軸下行切削運動和上行空程運動的時間比例,根據油腔截面積比例將其時間比例改變為1∶2,即滿足慢速切削快速空程返回,工作效率得到很大提高。則讓刀電動機需要頻繁地加減速,不利于數控系統的穩定。通過分析共軛雙凸輪讓刀機構的運行特性,通過設計凸輪曲線就可以解決上述問題。
本文以數控插床滿足等速往復運動的讓刀機構為例,對其雙共軛凸輪輪廓線進行設計;滿足下行與上行時間比2∶1的讓刀機構雙共軛凸輪輪廓線原理與其類似,不再贅述。
1 讓刀機構功能需求
圖1是伺服讓刀機構示意圖。
伺服電動機驅動的數控插床讓刀機構采用如下技術方案:伺服電動機可以根據主軸運動的位置進行數控調速,以滿足于讓刀機構與插削機構的運動周期同步。伺服電動機通過減速器和聯軸器將運動傳遞到凸輪軸上,共軛雙凸輪在任意時刻與撥叉上的兩個滾子均保持接觸,共軛雙凸輪曲線與各自所對應的滾子的接觸點嚙合,其凸輪形狀曲線滿足讓刀機構運動曲線特征,使撥叉進行往復擺動,撥叉帶動偏心軸往復擺動,偏心軸推動讓刀拉桿使得讓刀拉桿前端做往復移動,從而推動數控插床刀架形成讓刀運動。撥叉上的其中一個滾子的軸是小偏心軸,可以通過它的旋轉控制兩滾子與共軛凸輪的配合以彌補機加工的誤差。伺服電動機驅動的數控插床讓刀機構由于采用本技術方案,因而解決了讓刀機構和插削機構運動周期無法同步的問題。
具體實施方式:伺服電動機1帶動減速器2,通過聯軸器3帶動凸輪軸4轉動,凸輪軸4推動滾子,使撥叉7擺動,撥叉7通過鍵帶動偏心軸9擺動,偏心軸9帶動讓刀拉桿8往復運動。
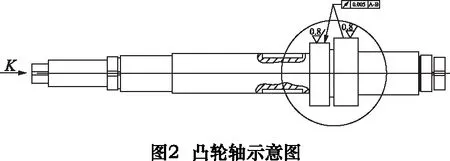
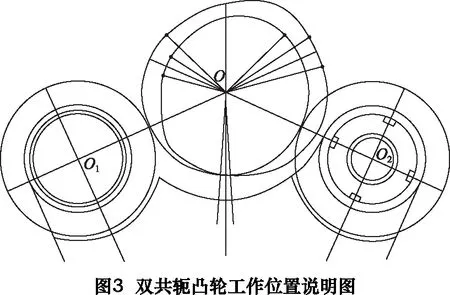
伺服讓刀機構的機械零件均可設計,其中設計難度最大的是凸輪軸的雙共軛凸輪輪廓線部分。圖2是凸輪軸的示意圖,圓圈中的部分即為其雙凸輪部分。圖3是其雙共軛凸輪部分工作位置說明圖。

讓刀機構需要滿足的讓刀運動的運動關系如圖4所示。左側陰影部分是被加工工件,右側封閉曲線是刀具運行軌跡的原理圖。刀具在一個往復沖程中需要向工件的反方向運動一次。
如何設計刀具的運動軌跡,亦即如何設計讓刀凸輪輪廓線,是本文的主要內容。要通過輪廓線的設計與計算,使得讓刀運動規律振動最小化,避免剛性沖擊和柔性沖擊。所謂無沖擊,即所受力連續、不突變且平滑過渡,數學表達為:運動曲線的一階導數連續且可導、運動曲線的二階導數連續。
2 共軛雙凸輪輪廓線設計
2.1 中心孔距及基本參數的確定
選擇“5-12-13”勾股序列作為本文的參照,該序列可以很方便地上下擴展。根據類比法和讓刀力量的需求計算,選擇“5-12-13”勾股序列的18倍作為本文的設計參數。
即凸輪軸與偏心軸的中心孔距Lcen為:
Lcen=13×18=234 mm
凸輪軸與兩個滾子的初始距離Lo為:
Lo=5×18=90 mm
偏心軸與兩個滾子的中心矩Larm為:
上述參數的空間位置關系,如圖5所示。
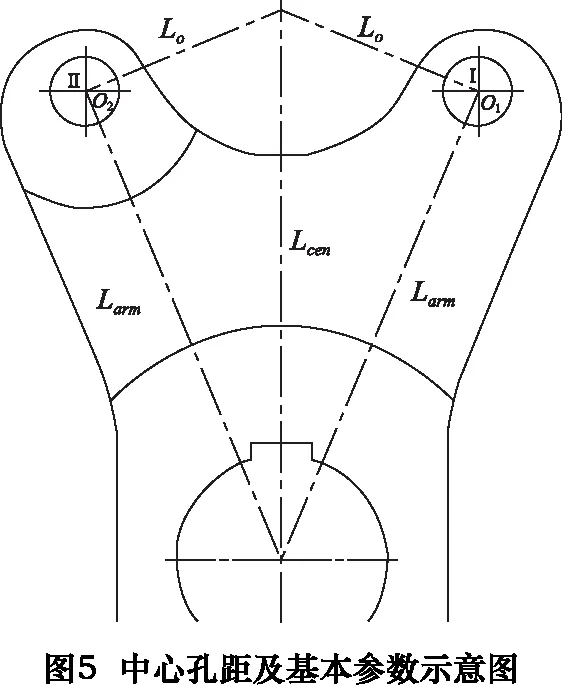
2.2 讓刀量及凸輪升程的確定
根據機床設計要求,數控插床的讓刀量需求為不小于0.80 mm。
根據供應商INA公司軸承的型號規格,將滾子的半徑R確定為:
RL=RR=40 mm
由此,凸輪的標定半徑Rmid為:
Rmid=Lo-RL=50 mm
根據讓刀量需求,將主動凸輪最小半徑Rsmall預設為:
Rsmall=38 mm
并將偏心軸偏心距Lwinck進行預設,
Lwinch=16 mm
凸輪參數預設結果如圖6所示。
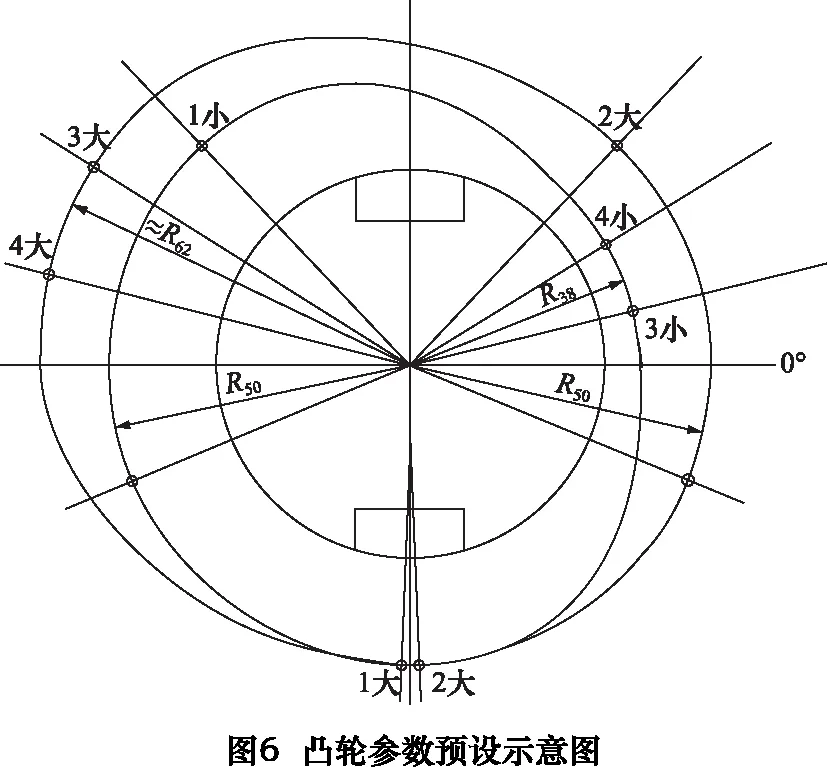
根據上述參數,對核算讓刀量得:
(arcsin[Lo/Lcen]-arccos[(Lcen2+Larm2-
(RL+Rsmall)2)/(2×Lcen×Larm)])×
Lwinch·π/180= 0.889 4 mm
扣除由于零件間隙及計算方法的誤差10%,0.889 4 mm>0.80×1.1 mm上述參數滿足要求。
2.3 圓弧轉角的確定
根據插床設計經驗,工件厚度/沖程長度>93%。
計算得圓弧轉角:2×arcsin[0.93]=137°
為了計算的簡便和工作的可靠性,將圓弧轉角取值138°。
2.4 升降函數的確定
由機械原理凸輪傳動知識可知,“等加速等減速”和“余弦加速度”等運動規律存在柔性沖擊,而“3-4-5多項式”運動規律,不存在柔性沖擊,適用于“高速中負荷”的場合。本文凸輪過渡曲線采用“3-4-5多項式”,為了避免沖擊,該多項式要滿足以下條件:
(1)首尾與圓弧曲線相接。
(2)一階導數連續,并且首尾點的一階導數為0。
(3)二階導數連續,并且首尾點的二階導數為0。
至于是否有必要將升降函數曲線的最高階次升至7次函數,并且要求“三階導數連續、首尾點的三階導數為0”呢?其比較結果,如圖7所示,7階函數的沖擊反應會更小,但其首尾段的直線延伸更明顯,不利于讓刀機構的快速讓刀運動。所以選擇5次函數,是正確可取的。

由此,設定5次函數為:
f[x]=Ak5×(x5)+Bk5×(x4)+Ck5×(x3)+Dk5×(x2)+Ek5×x+Fk5
2.5 凸函數校核及最小升降角度計算
為了該凸輪曲線具有大砂輪加工性和運動平穩性,該凸輪曲線須為凸曲線。可以利用以下公式對其凹凸性進行驗證。
gx=f[x]×cos[x]
gy=f[x]×sin[x]
gxd1=D[gx,x]
gyd1=D[gy,x]
gxd2=D[gx,{x,2}]
gyd2=D[gy,{x,2}]
注:本文中D[gx,x]是對gx關于參數x求一階導數,其他表示方法類同。
gd1=gyd1/gxd1
其凹凸性證明函數為:
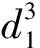
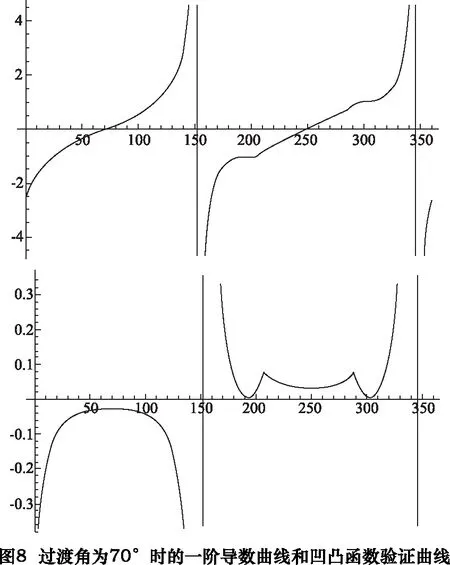
經過反復驗算,本凸輪輪廓線的最小過渡角度為70°。當過渡曲線的過渡角為70°時,其一階導數曲線和凹凸函數驗證曲線如圖8所示。由圖8可見,該曲線在過渡部分,二階導數大于0,該曲線為凸曲線。亦即:只要大于70°的過渡曲線都滿足凸曲線的特性。
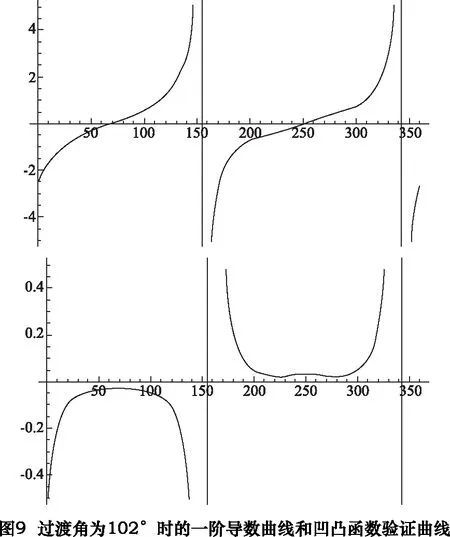
經過反復計算,當過渡角為102°時的曲線其一階導數曲線和凹凸函數驗證曲線最平滑,在滿足無沖擊的前提下,還能做到運動關系相對最平穩。當過渡曲線的過渡角為102°時,其一階導數曲線和凹凸函數驗證曲線如圖9所示。
2.6 升降函數的參數計算
按照2.4節設定的5次函數曲線方程和需要滿足的條件,求解下列方程組,
Solve[
{
f[x]|x=PointS2=Rmid
f[x]|x=PointS3=Rsmall
}
]
上述方程中所列PointS2,PointS3為過渡曲線的起點和終點。PointS1,PointS2,PointS3,PointS4為其過渡點,同于圖6中的“1小-2小-3小-4小”。求得方程的6個特征參數{Ak5,Bk5,Ck5,Dk5,Ek5,Fk5},即可求得過渡曲線,變換特征參數的正負,即可求得與其對稱的過渡曲線。
2.7 主動凸輪曲線設計
根據2.2節確定的凸輪遠休止與近休止半徑和由2.5節求得的過渡曲線方程,組合列出主動凸輪曲線如下:
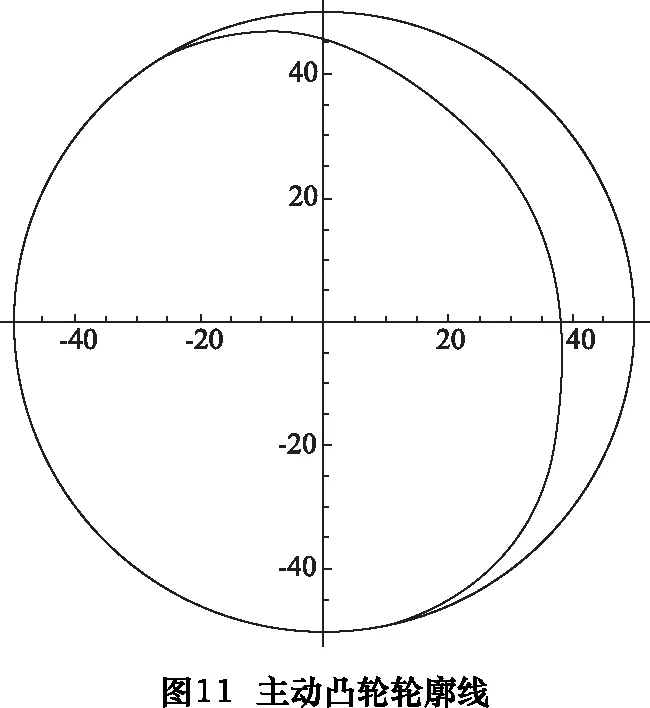
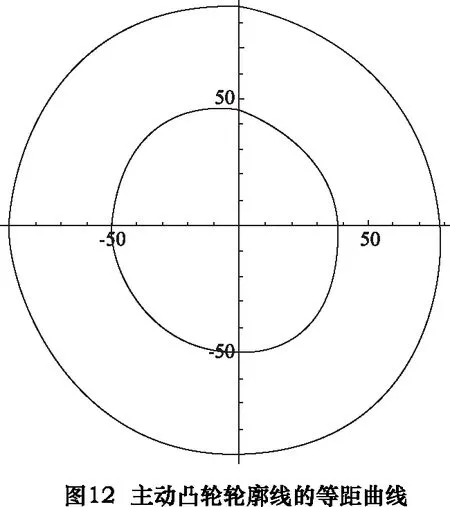
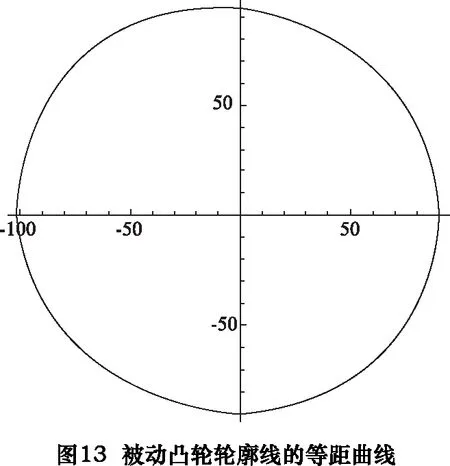
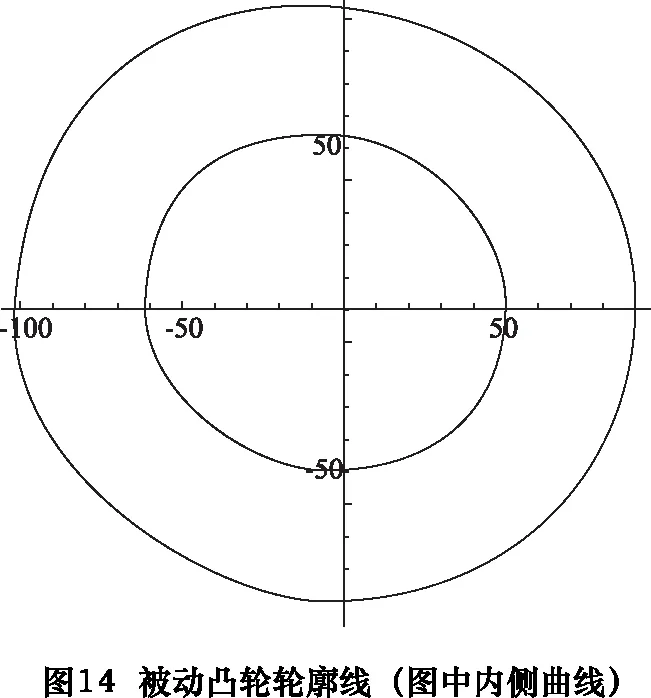
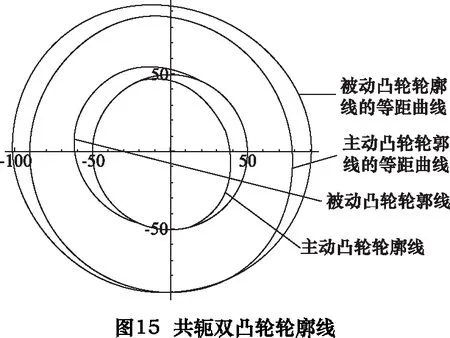
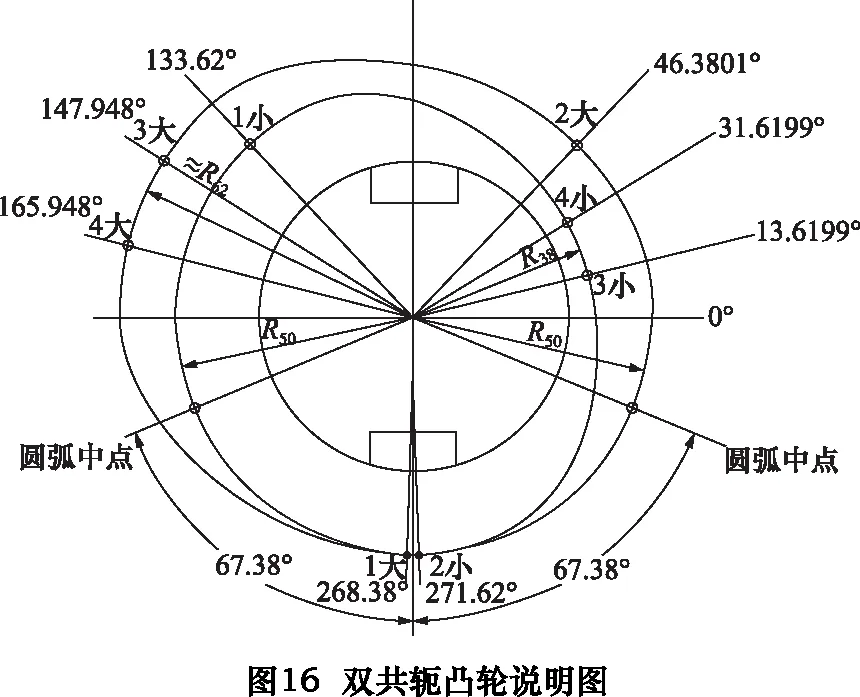
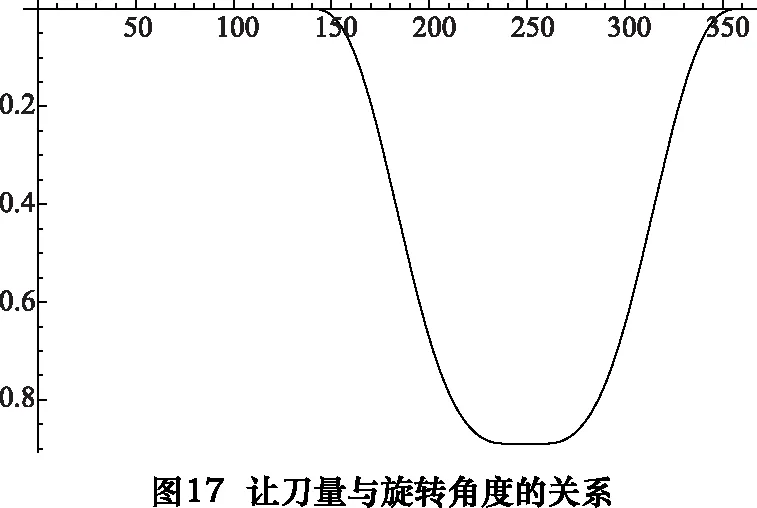
f[x_] :=Rmid/;PointS1≤x f[x_] :=Am5×x5+Bm5×x4+Cm5×x3+Dm5×x2+Em5×x+Fm5/;PointS2 ≤x f[x_] :=Rsmall/;PointS3 ≤x f[x_] :=Ar5×x5+Br5×x4+Cr5×x3+Dr5×x2+Er5×x+Fr5 /;PointS4 ≤x≤PointS5 求得主動凸輪展開曲線如圖10所示,主動凸輪輪廓線如圖11所示。 根據下列公式組合, fx=f[x]×cos[x] fy=f[x]×sin[x] dfx=D[fx,x] dfy=D[fy,x] xLeftO=fx+RL×dfy/Sqrt[dfx2+dfy2] yLeftO=fy-RL×dfx/Sqrt[dfx2+dfy2] 求取主動凸輪輪廓線的等距曲線,亦即與主動凸輪嚙合的滾子的中心與主動凸輪相比較的軌跡曲線。其等距曲線計算結果,如圖12所示。圖中,內側曲線為主動凸輪輪廓線,外側曲線為其等距曲線。 根據圖5所示的中心矩及撥叉基本參數,利用2.8節求解得的主動凸輪輪廓線的等距曲線,求解被動凸輪輪廓線的等距曲線,如圖13所示。 同樣利用2.7節所列公式,改變其法線方向,即可以求取被動凸輪輪廓線,如圖14所示。 至此,已經求取共軛雙凸輪的兩條輪廓線,其位置關系和曲線表示如圖15所示。將上述主動凸輪輪廓線和被動凸輪輪廓線的曲線以等距離點的方式輸出為數控凸輪磨床可以識別的數控程序,即可完成對凸輪軸的凸輪輪廓線磨削加工。 經過求解其過渡點的角度坐標,將其詳細輪廓線描述如下(如圖16所示)。圖16中由“1小—2小—3小—4小—1小”所連接的封閉曲線為其中的小凸輪的曲線,小凸輪即為主動凸輪,其曲線的變化決定了讓刀運動的變化規律。 其中,“1小—2小”區間為R=50 mm的圓弧,“3小—4小”區間為R=38 mm的圓弧,“2小—3小”和“4小—1小”區間為對稱的降程曲線和升程曲線。 圖16中由“1大—2大—3大—4大—1大”所連接的封閉曲線為其中的大凸輪的曲線,大凸輪即為被動凸輪,其曲線的變化決定了是否可以使得兩個凸輪曲線與其對應的兩個滾子在任意時刻接觸。其中,“1大—2大”區間為R=50 mm的圓弧,“3大-4大”區間為的圓弧,其半徑由計算得約等于62 mm,“2大—3大”和“4大—1大”區間為計算所得的對稱的降程曲線和升程曲線。 根據上述計算結果,求解驗算讓刀量與旋轉角度的關系(如圖17所示)和讓刀量與插削位置的關系(如圖18所示),并以圖19局部表達了其過渡區間的運動曲線。 由圖17~19可知,讓刀量和讓刀運動關系平滑過渡,滿足題設的條件。 利用上述計算結果加工的雙共軛凸輪應用現場照片如圖20所示。 實際應用表明,本文所述雙共軛凸輪無沖擊,上下擴展適應性強,可在插床中廣泛應用。 [1]張策.機械原理與機械設計[M].北京:機械工業出版社,2011. [2] 李瑰賢.空間幾何建模及工程應用[M].北京:高等教育出版社,2007. [3] 蔡自興,謝斌.機器人學[M].北京:清華大學出版社,2015. [4] 羅伯特·諾頓,機械設計[M].4版.北京:機械工業出版社,2016. [5]余洋, 石博強, 侯友山.結構剛度對液壓伺服系統穩定性影響分析[J].農業工程學報, 2011, 27(12):32-35. [6] 陳新元, 湛從昌, 付曙光.伺服液壓缸動摩擦力的高精度測試方法研究[J].機械設計與制造, 2011(3):116-118.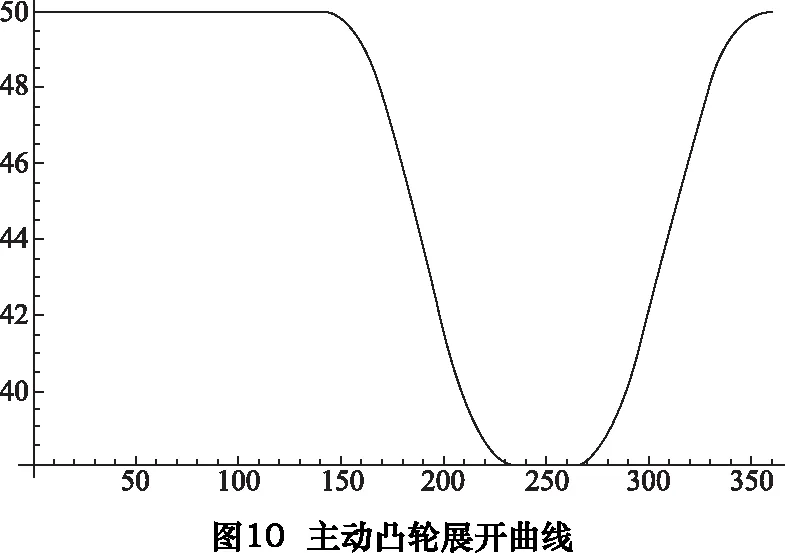
2.8 求解主動凸輪輪廓線的等距曲線
2.9 求解被動凸輪曲線
2.10 數據輸出
2.11 驗證讓刀量和運動關系
3 共軛雙凸輪設計結果及實際應用