空間3自由度并聯(lián)機構(gòu)運動螺旋運動分析

王麗，王益軒

（1.西安工程大學(xué)，陜西 西安 710048；2.陜西工業(yè)職業(yè)技術(shù)學(xué)院，陜西 咸陽 712000）

引言

由并聯(lián)機構(gòu)發(fā)展起來的各種并聯(lián)機器普遍具有剛度精度高、承載能力強而運動負(fù)荷小的優(yōu)點，但是并聯(lián)機構(gòu)復(fù)雜的結(jié)構(gòu)特征使得它的許多機構(gòu)學(xué)問題變得極其困難，為此諸多的數(shù)學(xué)方法被引用到機構(gòu)的理論研究中。盡管各種方法所表示的機構(gòu)學(xué)特征實質(zhì)是相同的，但卻有不同的特點。螺旋理論在機構(gòu)的許多問題的研究中都有應(yīng)用， Yang[1]提出一種利用有限螺旋合成3自由度并聯(lián)機構(gòu)的方法，得到機構(gòu)的空間拓?fù)浣Y(jié)構(gòu)。陳子明[2]通過分析機構(gòu)螺旋系線性相關(guān)的條件得出奇異位形的判別方程。柴馨雪[3]利用螺旋理論建立機構(gòu)運動學(xué)反解方程，得到機構(gòu)約束奇異和運動學(xué)奇異的判別條件。Jaime[4]利螺旋理論分析了3-CRS并聯(lián)機構(gòu)的運動學(xué)，得到機構(gòu)的輸入輸出速度、加速度關(guān)系方程。Guan[5]用螺旋表示每個關(guān)節(jié)的運動，利用反螺旋的性質(zhì)得到每個分支施加給動平臺的約束螺旋，分析了機構(gòu)發(fā)生奇異的三種條件。熊有倫[6]以矢量積和微分運動分析的方法建立機器人機構(gòu)的速度雅克比矩陣，黃真[7,8]以機構(gòu)的影響系數(shù)建立并聯(lián)機構(gòu)構(gòu)件之間的速度關(guān)系矩陣。本文將相鄰構(gòu)件的相對運動表示成運動螺旋，以它們的線性組合構(gòu)造運動鏈末端構(gòu)件的運動螺旋，導(dǎo)出機構(gòu)正向和逆向速度關(guān)系方程。

1 機構(gòu)的結(jié)構(gòu)約束

空間3自由度并聯(lián)機構(gòu)動平臺通過三條相同的運動鏈與基座相連，每條支鏈具有一個轉(zhuǎn)動副、一個移動副和一個球面副，如圖1所示。

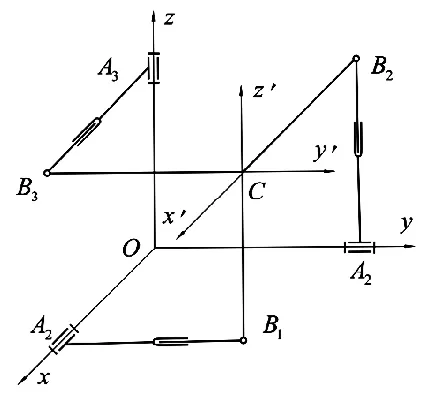
圖1 空間3自由度并聯(lián)機構(gòu)運動簡圖

選取參考坐標(biāo)系 O-xyz 和動坐標(biāo)系 C-x′y′z′，Br在坐標(biāo)系O-xyz的位置矢量

B′r——Br在坐標(biāo)系 C-x′y′z′的位置矢量

R——坐標(biāo)系 C-x′y′z′對 O-xyz 旋轉(zhuǎn)變換矩陣

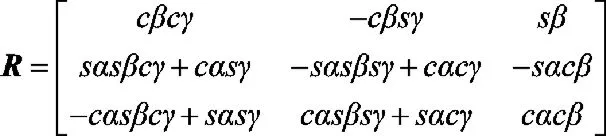
α、β、γ——動坐標(biāo)系 C-x′y′z′繞 x、y、z軸的轉(zhuǎn)角

受移動副和轉(zhuǎn)動副的結(jié)構(gòu)限制，Br始終位于與坐標(biāo)面平行的平面上，有一個坐標(biāo)保持不變。

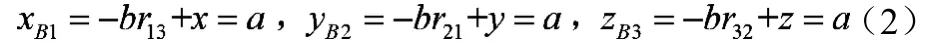
式中a,b——分別為OAr和BrC的長度。由式(2)可得，

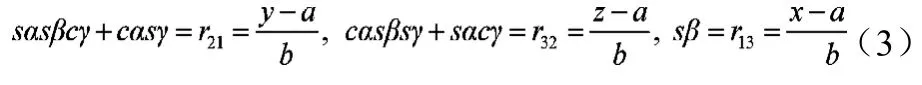
上式表明，動平臺的位置參數(shù)和姿態(tài)參數(shù)并非彼此獨立，將上式對時間t求導(dǎo)，可得到動平臺平動速度和轉(zhuǎn)動角速度之間的關(guān)系，即機構(gòu)運動約束。

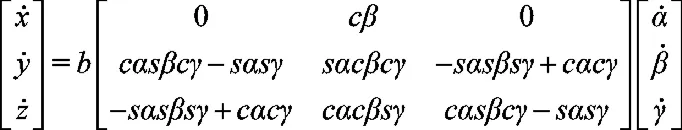
2 構(gòu)件的瞬時運動螺旋

為了分析動平臺的瞬時運動，將機構(gòu)的球面副用三個軸線垂直相交的轉(zhuǎn)動副表示，如圖2所示。每個分支有5個活動構(gòu)件，用0,1,…,5標(biāo)記，在分支r中，中間連桿i (i=1,2,3,4)都有兩個關(guān)節(jié)，與它固連的坐標(biāo)系記為，軸取在前一個關(guān)節(jié)軸線方向，軸取在連桿兩關(guān)節(jié)軸線的公法線方向。與機架固連的坐標(biāo)系記為，取成和重合，取成關(guān)節(jié)1轉(zhuǎn)角度量的起點方向。與構(gòu)件5（即動平臺）固連的坐標(biāo)系，軸取在關(guān)節(jié)軸線上，軸取成當(dāng)該關(guān)節(jié)轉(zhuǎn)角等于零時與軸重合。在選取坐標(biāo)系后，可以從中定義連桿運動學(xué)參數(shù)（D–H參數(shù)），如表1所示。

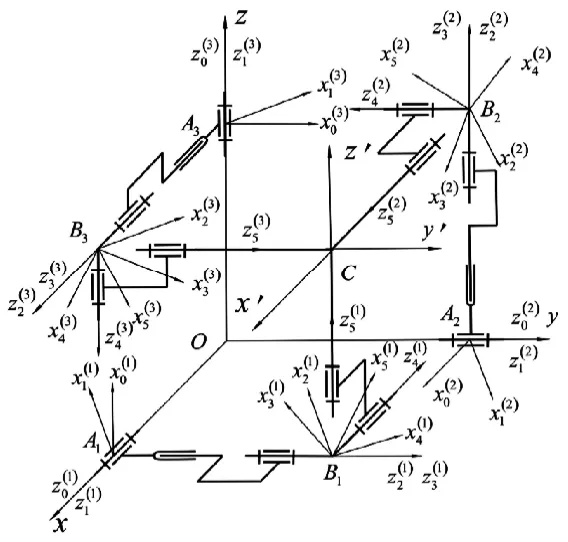
圖2 空間3-RPS并聯(lián)機構(gòu)等效運動簡圖

表1 連桿運動學(xué)參數(shù)（D–H參數(shù)）

在分支中，如果構(gòu)件i與i-1通過轉(zhuǎn)動關(guān)節(jié)相連，它們之間的相對運動是繞關(guān)節(jié)軸線的轉(zhuǎn)動，軸線的空間位置可以用一個單位螺旋表示：

如果構(gòu)件i與i-1通過移動關(guān)節(jié)相連，它對構(gòu)件i-1的相對運動是沿著關(guān)節(jié)軸線方向的平動，移動關(guān)節(jié)的運動螺旋。

3 動平臺的螺旋運動描述

在機構(gòu)路徑規(guī)劃中，一般是按作業(yè)性質(zhì)給出動平臺角速度矢量ωS和動平臺上最具特征的稱參考點P的線速度vp,將動平臺的運動用螺旋表示：

其中，角速度矢量ωS與坐標(biāo)原點的選取無關(guān)，ωS0代表動平臺上與坐標(biāo)原點重合的那一點的速度。螺旋的節(jié)距是原點不變量，如果將原點選在動平臺的P點，則動平臺的運動螺旋為：

這樣便能求出動平臺運動螺旋的節(jié)距：

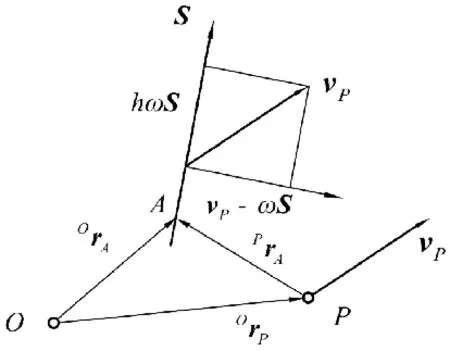
圖3 運動螺旋分解

將速度vp沿著角速度矢量及其垂直方向進行正交分解，如圖3所示，在角速度矢量方向的分量為，另一分量為，所以式(8)可以寫成以下兩個螺旋之和第一個螺旋中是一個線矢量，由它可以確定出螺旋ωS/轉(zhuǎn)動軸線在坐標(biāo)系{P}的位置方程：

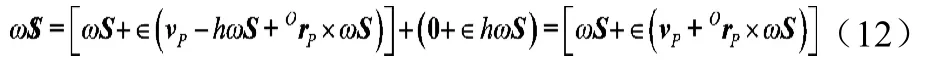
4 并聯(lián)機構(gòu)正向運動學(xué)

并聯(lián)機構(gòu)的正向運動學(xué)即是由主動關(guān)節(jié)速度求得動平臺速度，動平臺通過分支上的運動鏈連接到基座，它的運動螺旋應(yīng)該是分支所有運動螺旋的線性組合。

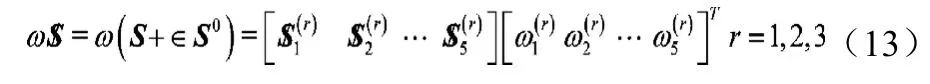
對于任意兩個分支：

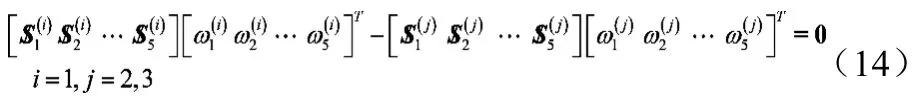
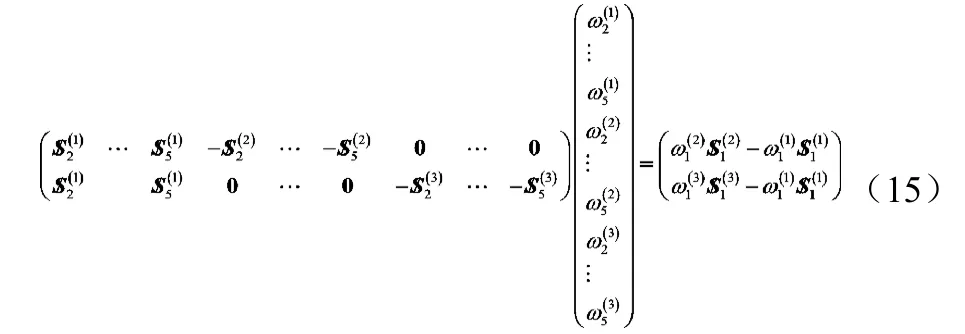
上式是以全部從動關(guān)節(jié)速度為未知數(shù)的線性代數(shù)方程組，可以從中解得所有關(guān)節(jié)速度，動平臺的瞬時運動螺旋可以由式(13)從任意一個分支中得到。

5 并聯(lián)機構(gòu)逆向運動學(xué)

設(shè)剛體的瞬時運動螺旋和為受到的力螺旋分別為：

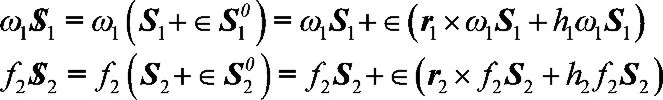
剛體以角速度ω1繞軸線S1轉(zhuǎn)動又以速度h1ω1沿軸線移動，同時又受到沿S2方向的作用力f2S2和力偶矩h2f2S2，兩螺旋的互易積，即一個螺旋的原部矢量與另一個螺旋的對偶部矢量的數(shù)量積之和，它代表了剛體的瞬時功率。如果兩螺旋互易積等于零，則它們互為反螺旋，如果螺旋用坐標(biāo)表示，互逆性條件可以表示成：

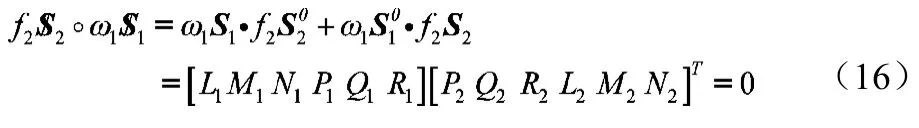
機構(gòu)的逆向運動學(xué)即是由動平臺速度求得所有關(guān)節(jié)速度，式(13)包含了每個分支未知的關(guān)節(jié)速度變量，而給出的等式卻有6個，在求解時必須考慮動平臺受到的約束。現(xiàn)在從每個分支后面關(guān)節(jié)開始向前遞推，并僅以第一個分支為例說明求解過程，其余分支的求解也類似。機構(gòu)每個分支5個關(guān)節(jié)運動螺旋構(gòu)成Ⅴ系螺旋，因而有唯一的反螺旋，記作，由反螺旋的性質(zhì)式(16)，得：

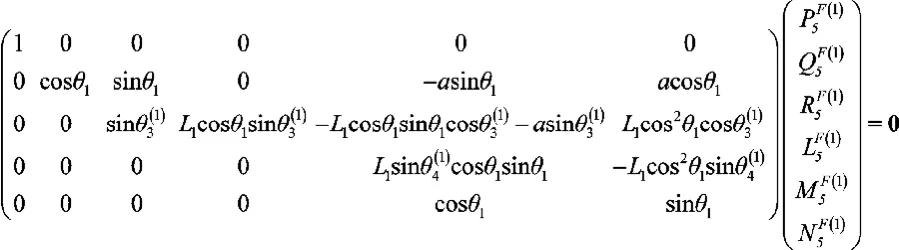
系數(shù)矩陣右下角的R2×2分塊矩陣的行列式等于零，所以方程解向量的最后兩個分量必須為零，剩下的前3個方程含有4個未知數(shù)，需要指定其中的一個，解得反螺旋。

反螺旋的表示式中有一個獨立的未知參數(shù)x4可以任意取值，但不能取為0。為了求第5個關(guān)節(jié)速度，取前四個關(guān)節(jié)的運動螺旋，它們構(gòu)成了一個Ⅳ系螺旋，有兩個線性無關(guān)的反螺旋，滿足為其中的一個，從中解得反螺旋系：

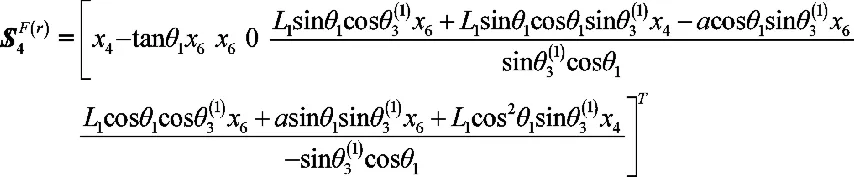
它有兩個獨立的參數(shù)x6和x4，可以任意取值，對比和選取其中與線性無關(guān)的哪一個對式(13)的兩邊作互易積：

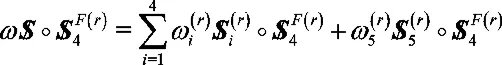
相逆的兩螺旋互易積等于零，上式右邊第一項等于零，從而求得：

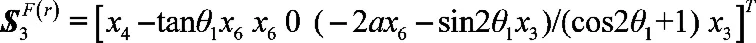
它有3個獨立的未知參數(shù)x6、x4和x3，可以任意取值，選取其中與和線性無關(guān)而的哪一個對式(13)的兩邊作互易積：

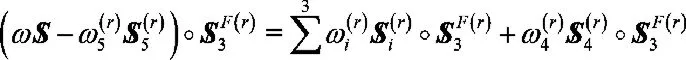
相逆的兩螺旋互易積等于零，上式右邊第一項等于零，從而求得：

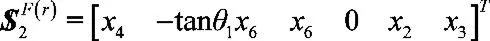
它有4個獨立的未知參數(shù)x6、x4、x3和x2，可任意取值，選取其中與和線性無關(guān)的哪一個對式(13)的兩邊作互易積：

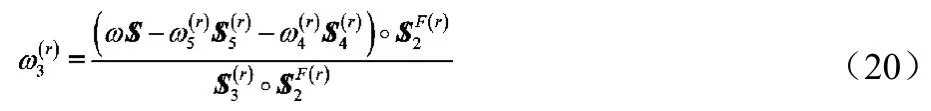
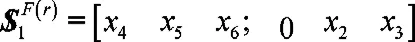
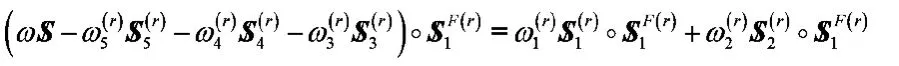
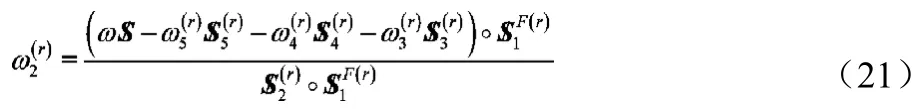
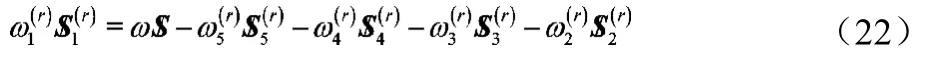
6 應(yīng)用實例

給定機構(gòu)結(jié)構(gòu)參數(shù)和動平臺的運動規(guī)律：a=980mm，b=600mm。

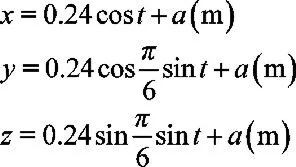
按式(22)和(21)可求得機構(gòu)所有主動關(guān)節(jié)和移動關(guān)節(jié)速度，如圖 4所示。主動關(guān)節(jié)轉(zhuǎn)動角速度的變化范圍為–0.2～0.2rad.s-1，移動關(guān)節(jié)速度的變化范圍為–0.3～0.3 m.s-1，將它們分別與動平臺的平動速度和轉(zhuǎn)動角速度比較，它們的比值在一定程度代表了機構(gòu)瞬時功率的傳遞關(guān)系。

7 結(jié)論

（1）將機構(gòu)的關(guān)節(jié)相對運動表示成運動螺旋，得到并聯(lián)機構(gòu)的正向運動學(xué)方程，動平臺及所有從動關(guān)節(jié)的運動速度都可以由主動關(guān)節(jié)速度線性地表示出來。

（2）螺旋理論對機構(gòu)每個分支采用從后向前遞推的方法，確定不同階螺旋系的反螺旋，得到所有關(guān)節(jié)速度與動平臺速度的關(guān)系方程。

[1] Shuo fei Yang, Tao Sun ,Tian Huang, etal. A finite screw approach to type synthesis of three-DOF translational parallel mechanisms [J].Mechanism and Machine Theory,2016, 104:405-419.

[2] 陳子明,黃坤, 劉曉檬.空間單環(huán)R/PSC機構(gòu)的運動和奇異分析[J].機械工程學(xué)報,2016,52 (13): 17-24.

[3] 柴馨雪,項濟南,李秦川.2-UPR-RPU 并聯(lián)機構(gòu)奇異分析[J].機械工程學(xué)報,2015,51(13):144-151.

[4] Gallardo-Alvarado Jaime. Kinematics of a Class of Three-Legged Parallel Manipulators by Means of Screw Theory [J]. Ingenieria Investigacion Y Tecnologia, 2016, 17(2):191-200.

[5] Li-Wen Guan, Jin-Song Wang, Li-Ping Wang. Mobility Analysis of the 3-UPU Parallel Mechanism Based on Screw Theory[C]. Procee-dings of the 2004 International Conference on Intelligent Mechatro-nics and Automation Chengdu, China, 2004, 309-314.

[6] 熊有倫,丁漢,劉恩倉編著.機器人學(xué)[M].機械工業(yè)出版社1993.

[7] 黃真,趙永生,趙鐵石.高等空間機構(gòu)學(xué)[M].北京:高等教育出版社, 2006.

[8] 黃真,孔令富,方躍法著.并聯(lián)機器人機構(gòu)學(xué)理論及控制[M].北京:機械工業(yè)出版社,1997.