面向車輛操縱穩定性的主動差速器模型預測控制?

冀 杰，黃巖軍，李云伍，張 春，高書娜

前言

隨著人們對汽車主動安全性能要求的不斷提高，如何有效改善車輛在惡劣行駛工況下的操縱穩定性已經成為車輛動力學控制的重要研究領域。目前，對車輛左右兩側車輪施加不同的制動力并產生必要的校正橫擺力矩，是有效提升車輛操縱穩定性的重要手段，例如電子穩定程序(ESP)、車輛穩定控制系統(VSC)等。然而，此方法在提高車輛操縱穩定性的同時，會損失一定的汽車動力性能，難以滿足賽車或高性能運動型轎車對動力性能和駕乘樂趣的要求[1]。

近年來，汽車主動差速器概念的提出與研究為改善車輛操縱穩定性提供了一條新的思路。主動差速器能夠根據車輛的行駛工況和路面狀態，將驅動力矩主動分配給驅動軸兩側的驅動輪，從而產生主動橫擺力矩并使車輛跟蹤期望的橫擺角速度和車身側偏角[2]。該機構的工作原理與差速制動相似，都是充分利用了輪胎縱向力線性范圍大于側向力線性范圍的特性，而差速驅動的方法能夠在產生主動橫擺力矩的同時，解決傳統差速制動方法造成的動力性能損失過大的問題[3]。目前，國內外學者對主動差速器的動力學特性和驅動力矩分配控制進行了大量前期研究。例如，文獻[4]中首先提出了主動差速器的基本結構并對其動力傳遞過程和控制進行了介紹和分析。文獻[5]中建立了主動差速器的動力學以及運動學模型，并分析了傳動軸以及輪胎非線性力對主動橫擺力矩產生的影響。文獻[6]中應用二階滑模控制算法對車輛的橫擺角速度進行控制，并考慮了車輛運動工況的不確定性和控制變量的飽和特性，從而有效跟蹤車輛的期望橫擺角速度。然而，上述操縱穩定性控制方法主要以當前的橫擺角速度跟蹤誤差作為控制依據，無法預測并利用車輛未來的運動狀態信息，這與人類的實際駕駛操作行為存在較大的差異。近年來，模型預測控制逐漸成為車輛操縱穩定性和驅動力矩控制的重要研究方向之一，該方法能夠利用車輛動力學預測模型獲得未來有限時域內的車輛動力學狀態參數，并通過求解有限時域內有約束條件的最優控制問題，獲得主動差速器的驅動力矩分配比例并提高車輛的操縱穩定性[7]，例如，文獻[8]和文獻[9]中將模型預測控制方法應用到電動汽車輪轂電機的驅動力矩主動分配中，仿真結果證明了該方法在主動驅動力矩分配控制中的有效性，也為傳統動力車輛的主動差速器模型預測控制提供了實踐基礎。

基于以上分析，本文中建立了基于主動差速器的車輛動力學預測模型，分析了影響車輛操縱穩定性控制的控制變量約束和輸出變量約束，同時，將模型預測控制問題轉換為標準的二次規劃問題并利用內點法進行了求解。最后，在低附著系數路面上對基于主動差速器的整車操縱穩定性控制進行了仿真分析。仿真結果證明了提出的模型預測控制算法在操縱穩定性控制中的有效性，為賽車及高性能運動型轎車的綜合運動控制提供一條新的途徑。

1 車輛/主動差速器綜合預測模型

1.1 雙軸車輛線性動力學模型

假設(x，o，y)為固定于車輛質心處的車輛坐標系，所有角度均取逆時針方向為正且車輛在縱向運動方向的速度恒定為Vx，同時，忽略懸架系統及側傾運動對車輛動力學特性的影響，并在動力傳動系統中添加主動差速器動力學模型。建立如圖1所示的雙軸線性動力學模型示意圖。

該模型直接以車輛的前輪轉向角δ和驅動橋系統的輸入軸轉矩Ti作為系統輸入，并假設前、后軸上左右兩側的輪胎橫向力在車輛坐標系下對稱相等，分別用Fyf和Fyr表示，而后軸左右兩側的輪胎縱向力分別用Fxl和Fxr表示。本研究將通過控制主動差速器左右兩側的驅動力矩分配比例，進而在后軸兩側產生不同的輪胎縱向力以及主動橫擺力矩MY，達到提高車輛操縱穩定性的目的。前、后軸上輪胎橫向力及主動橫擺力矩可表示為

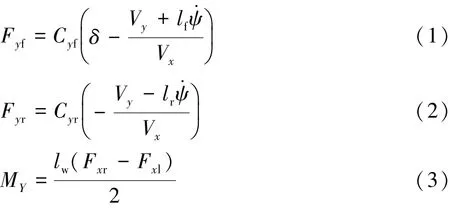
式中:Vy為車輛坐標系下的橫向運動速度；ψ為車輛的橫擺角度；Cyf和Cyr分別為前、后軸上兩個車輪合并后的側偏剛度系數；lf和lr分別為前軸和后軸到車輛質心的距離；lw為車輛后軸左右兩側車輪的輪距。

根據上述簡化原則，利用牛頓第二定律對車輛動力學模型進行分析，得到以前輪轉向角為輸入變量、以后軸左右兩側輪胎縱向力為控制變量的狀態空間模型為

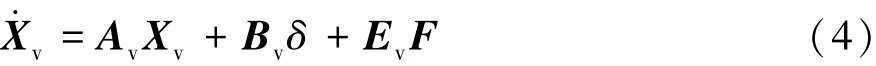
狀態變量Xv及各狀態矩陣可表示為

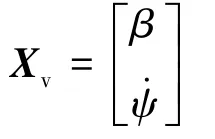
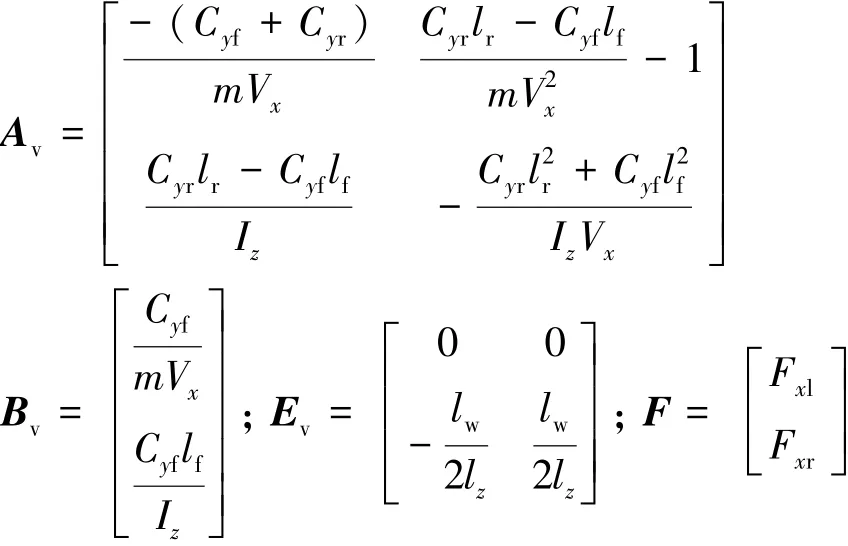
式中:β為車輛的車身側偏角；m為整車質量；Iz為整車繞z軸的轉動慣量。

1.2 主動差速器動力學模型

根據Kaoru Sawas提出的主動差速器結構，忽略傳動系統中各部件的彈性阻尼及其扭振、擺振等振動等因素，考慮輸入軸、輸出軸及驅動輪對主動差速器動力學的影響[10]，得出如圖2所示的主動差速器結構示意圖。

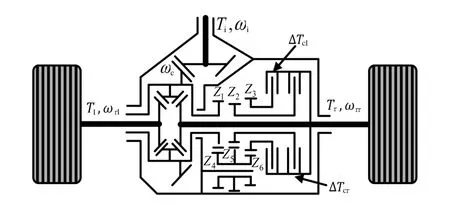
圖2 主動差速器的結構示意圖

對主動差速器中的齒輪組、主減速器齒輪、差速器行星齒輪以及制動器進行力矩平衡分析，并根據齒輪組中的齒輪齒數關系Z1＝Z2＝Z3＝42，Z4＝32，Z5＝36，Z6＝28，得到差速器輸入轉矩Td，驅動軸上左、右兩側制動器上的控制力矩ΔTcl和ΔTcr與兩側驅動力矩Tl和Tr之間的關系為

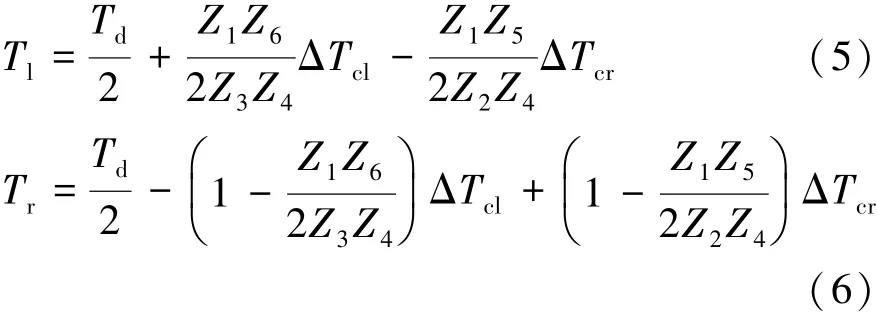
考慮主減速器的轉動慣量Iin、主動差速器的轉動慣量Id和主減速器的傳動比Nf，得到驅動橋系統的輸入軸轉矩Ti與差速器輸入轉矩Td之間的動力學關系為

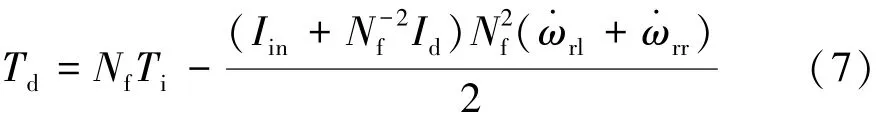
考慮左、右兩側輪胎的轉動慣量Iwl和Iwr以及左、右兩側驅動軸的轉動慣量Idl和Idr，并對主動差速器左、右兩側的驅動軸及車輪總成進行動力學分析，得

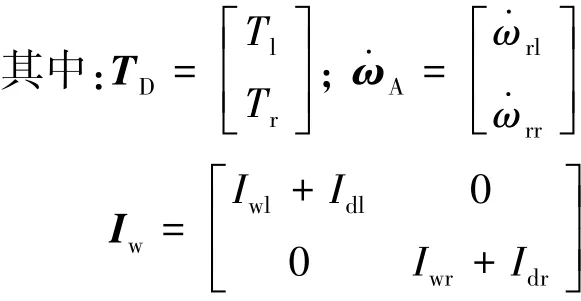
式中:Iw為車輪驅動軸總成的轉動慣量矩陣；Rw為車輪有效轉動半徑。

當輪胎的縱向力處于小滑移率區域時，輪胎力Fxl和Fxr與縱向滑移率σxl和σxr可近似看作線性關系:

式中:Cx和σA分別為驅動軸左、右兩側輪胎的縱向剛度矩陣和滑移率矩陣。

而車輪滑移率與車輪轉速之間的關系為

將式(7)、式(9)和式(10)代入到式(8)中，得到以后軸車輪縱向滑移率為狀態變量的主動差速器狀態空間模型為

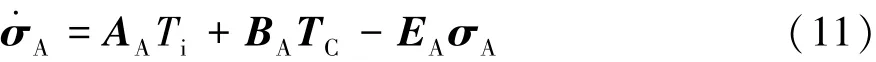
其中:

1.3 車輛/主動差速器綜合動力學預測模型

將輪胎縱向力計算公式(9)代入車輛動力學模型(4)中，并綜合主動差速器的動力學模型公式(11)，得到車輛/主動差速器綜合動力學狀態空間模型為

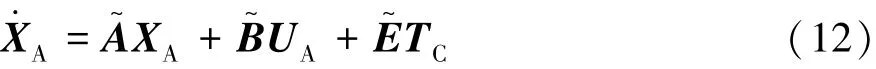
其中:

式中:XA為狀態變量；UA為輸入變量；TC為控制變量；Oi×j為具有 i行和 j列的零矩陣。

選擇狀態空間的輸出變量為 YA＝Xv＝[β]T， 得到輸出狀態方程為

利用歐拉方法對車輛動力學模型公式(12)和式(13)進行離散化處理(ΔT＝0.01s是系統的采樣時間)，得到線性定常離散時間的車輛動力學狀態空間模型:

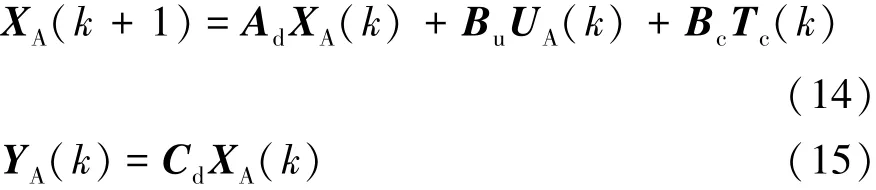
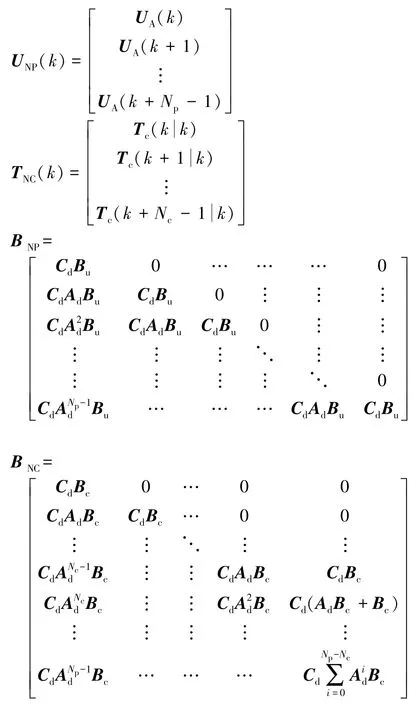
假設當前時刻k的所有狀態向量XA(k)是可測量或可估計的，利用迭代模型公式(14)得到未來某時刻的狀態變量XA(k+i)及輸出變量YA(k+i)預測值。設定預測時域為Np＝6，控制時域為Nc＝6。另外，(k+i k )表示當前k時刻對未來k+i時刻的車輛動力學狀態參數預測，最終得出車輛動力學輸出變量的模型預測狀態空間方程為

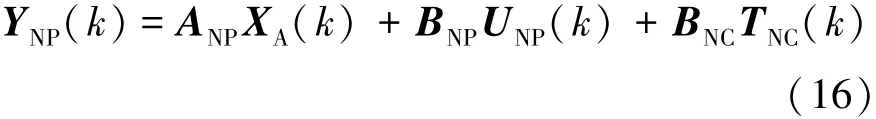
其中:

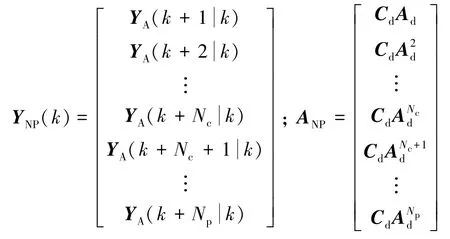
2 約束模型預測控制系統設計

車輛操縱穩定性模型預測控制的核心思想可描述為:在當前采樣時刻k，根據測量或估計的車輛動力學狀態變量XA(k)，獲得未來預測時域Np范圍內的輸出狀態信息YA(k+i k)，并基于期望信息在線求解約束最優化問題，最后將得到的控制變量作用于車輛動力學模型并不斷重復上述過程[11]。

2.1 目標函數

將車輛的操縱穩定性控制問題轉化為有限時域內的約束最優化問題[12]，定義能反映車輛操縱穩定性能指標的目標函數:

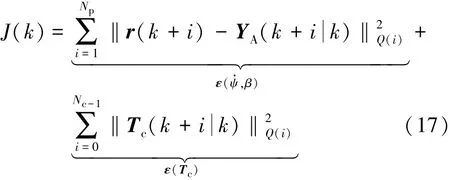
根據轉彎半徑R，前輪轉向角δ和車輛動力學模型參數，得到車輛在穩態轉向時的橫擺角速度δ和車身側偏角βδ參考值為

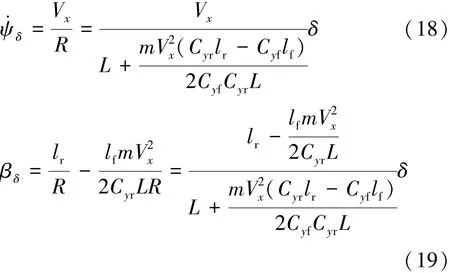
式中，L＝lf+lr，為車輛前、后車軸之間的軸距。

由于車輛的縱、橫向輪胎力具有非線性飽和特性，根據車輛行駛速度變化以及道路參數，可設定橫擺角速度ψ·max和車身側偏角βmax的范圍:

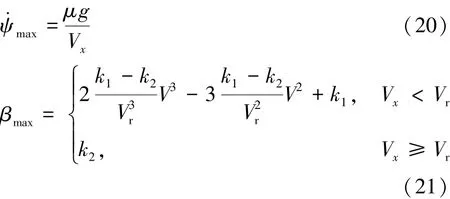
式中:μ為路面附著系數；g為重力加速度；Vr為車輛動力學的特征速度；參數k1和k2分別定為π/18和π/60[7]。

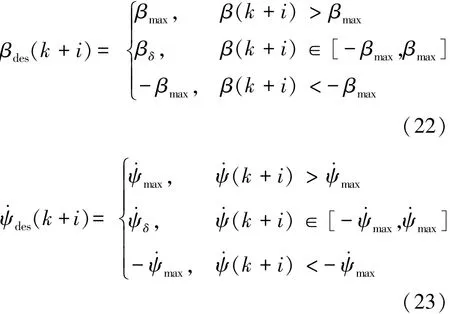
另外，根據差速器、傳動齒輪和制動器的運動學關系可知，對主動差速器左側和右側的制動器同時進行控制將會造成運動干涉。因此，設定左、右制動器的控制力矩范圍是ΔTc∈[-Tmax，Tmax]，當ΔTc>0時，表示右側制動器工作；而ΔTc＝0時，表示左右兩側制動器同時松開；當ΔTc＜0時，表示左側制動器工作，即:

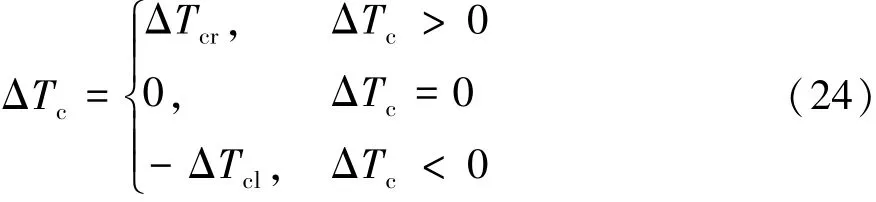
選擇目標函數控制輸入和跟蹤誤差的加權矩陣分別為R＝0.001·INc和Q＝I2Np，利用Um(k)表示控制時域Nc范圍內的控制力矩輸入向量:

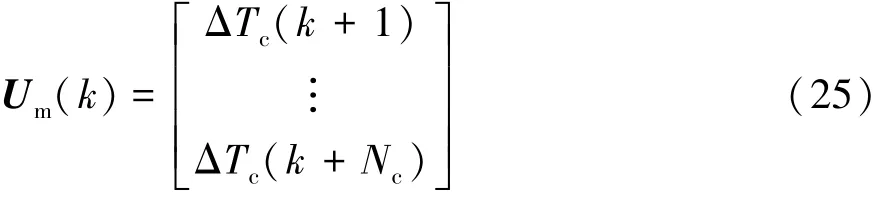
分別利用Rr(k)和Ym(k)表示預測時域Np范圍內的車輛運動參考信息和實際輸出狀態信息:

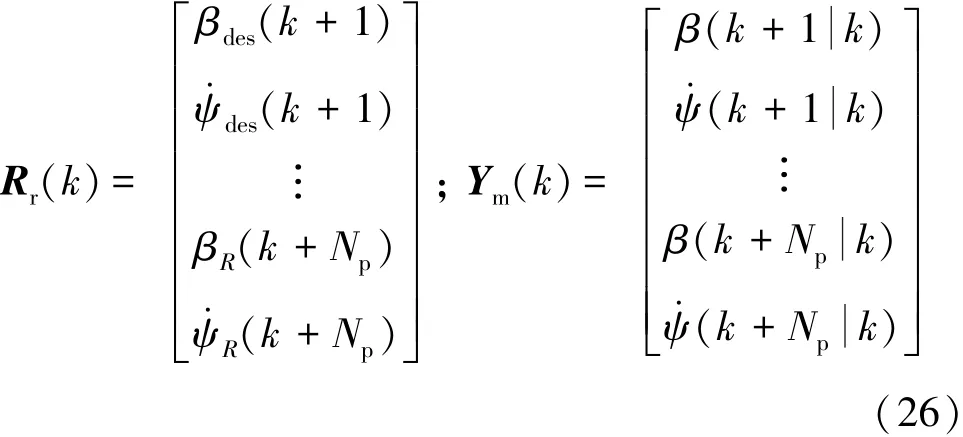
將式(25)和式(26)代入到目標函數式(17)中，得

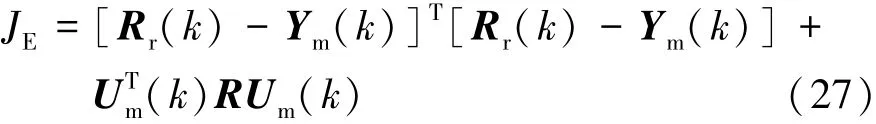
2.2 約束條件分析

由主動差速器的機械運動原理可知，根據驅動力矩的橫向傳遞方向及右側驅動軸與制動盤之間的速度差，能夠判斷對主動差速器的左側還是右側制動盤進行控制[13]，具體的控制規則如表1所示。

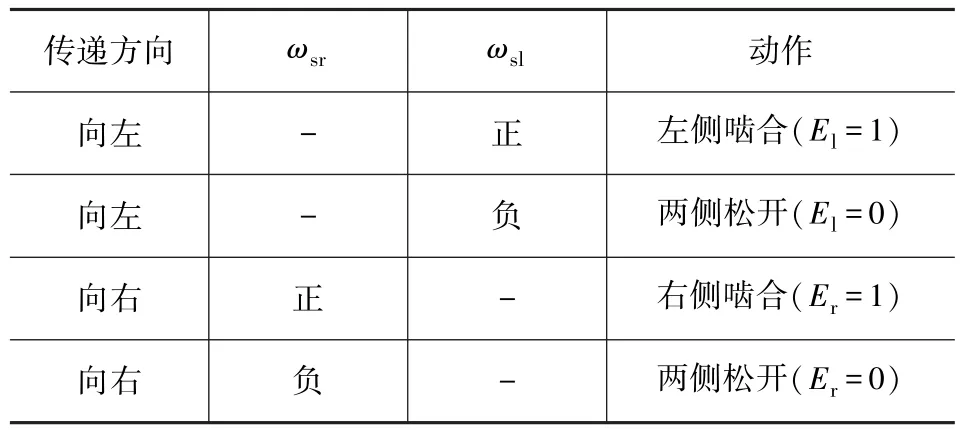
表1 主動差速器控制規則

其中，El和Er分別表示左、右兩側制動器的嚙合狀態，右側驅動軸與兩個制動器之間的速度差可表示為

式中:ωr為右側驅動軸的轉動速度；ωcl和ωcr分別為左側和右側制動器的轉動速度。

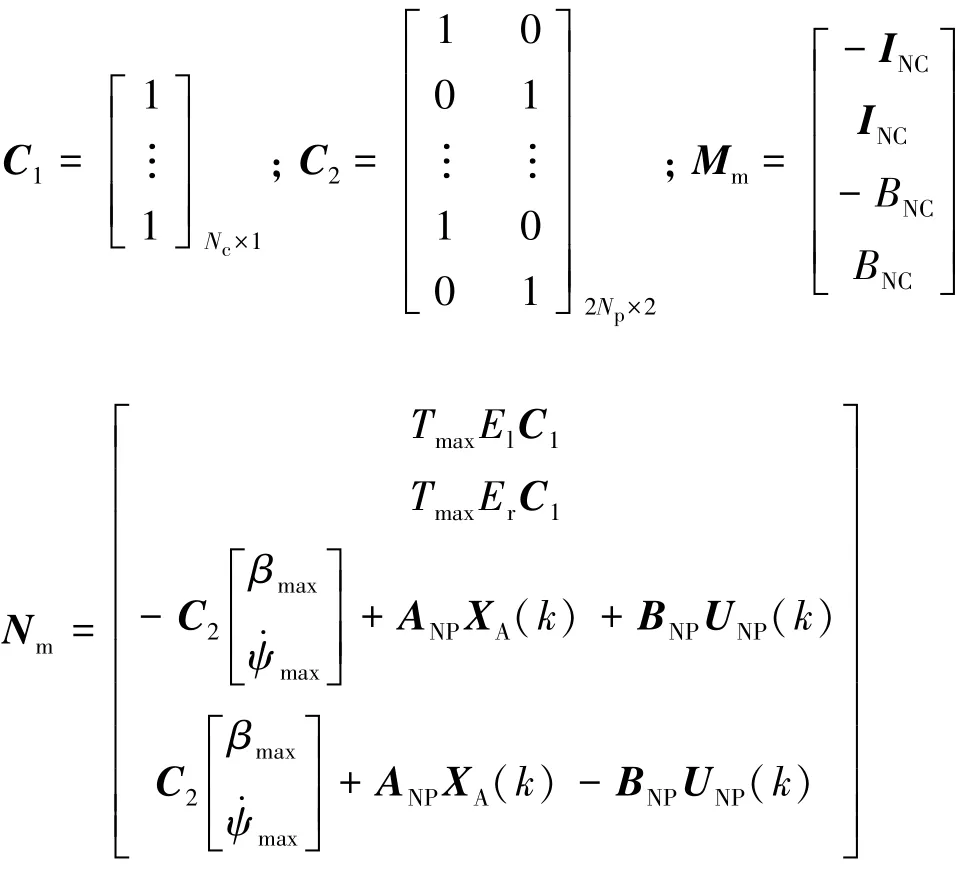
根據表1所示的主動差速器控制規則和控制力矩物理特性，可確定主動差速器控制力矩的Um(k)約束范圍；根據式(16)、式(20)和式(21)，可確定車輛動力學預測模型的橫擺角速度和車身側偏角的約束范圍。其不等式矩陣形式為

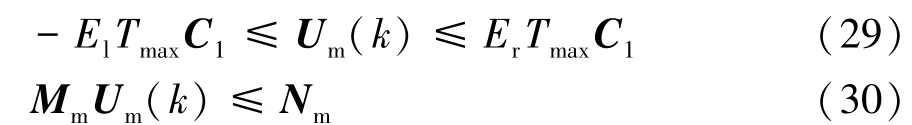
式中，Tmax為主動差速器左、右兩側制動盤的最大控制力矩極值。

其中:

2.3 模型預測控制求解

在模型預測控制問題的求解過程中，由于約束條件的存在，一般情況下難以直接得到式(17)的優化目標函數解析解，需要采用數值優化方法求解約束優化問題。由于目標函數是二次型的，動力學方程和時域約束條件是線性的，所以該約束優化問題可轉化為標準的二次規劃(quadratic programming，QP)問題描述。

將車輛動力學離散狀態空間預測模型的輸出變量(16)代入到模型預測控制的目標函數(27)中，并定義:

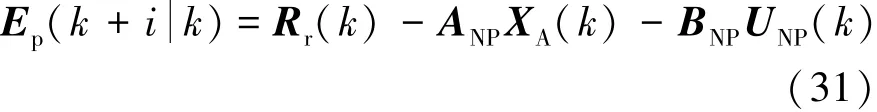
對目標函數進行整理，得

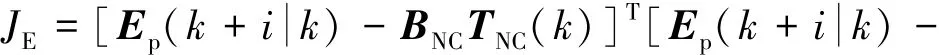
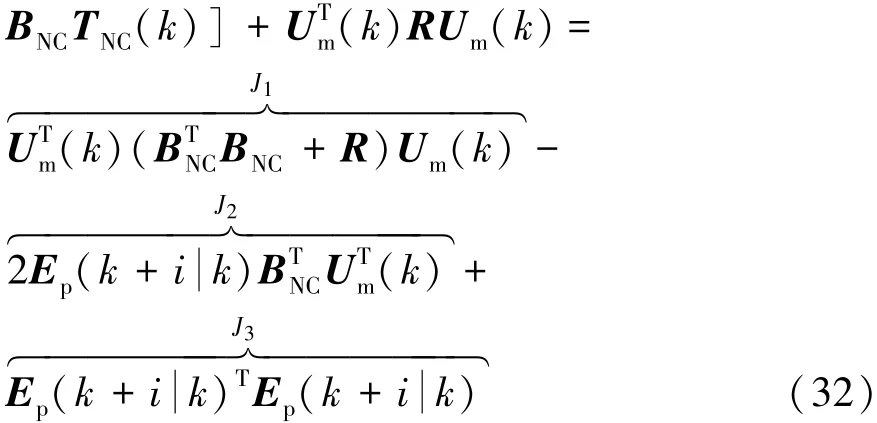
為獲得二次規劃問題的標準形式，設定二次規劃問題中的相容Hessian矩陣為Em，且梯度向量的獨立變量矩陣為Fm，分別表示為

由于式(32)中的常數項J3不影響主動差速器控制力矩序列Um的求解，因此，將以上兩個變量矩陣代入到目標函數(32)中，并與約束條件不等式(30)進行整理和轉換，得到如式(35)和式(36)所示的車輛操縱穩定性控制二次規劃問題標準形式。利用內點法求解該帶有線性約束的二次實函數，流程如圖3所示(更加詳細的求解過程請參考文獻[14])。

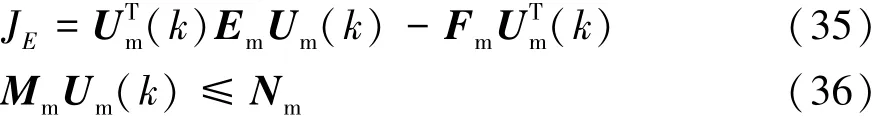
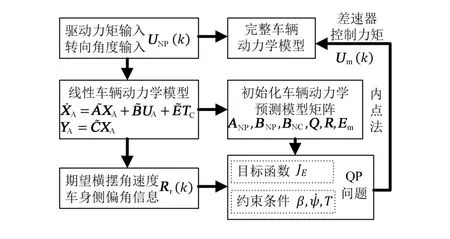
圖3 約束模型預測問題的內點法求解

3 仿真結果分析

為驗證模型預測算法在車輛操縱穩定性控制中的有效性，利用MATLAB/Carsim軟件進行聯合仿真分析。在轉向盤角度正弦輸入情況下，比較低附著系數路面上的模型預測控制車輛與無控制車輛之間的橫擺角速度以及車身側偏角參數變化，并分析主動差速器的工作過程及控制力矩變化。

本研究采用雙軸線性車輛動力學模型用于模型預測控制系統設計，其主要參數如表2所示，而仿真模型則是裝備了主動差速器的Carsim車輛動力學模型。

表2 車輛動力學預測模型參數

假設被控車輛以初始速度Vx＝20m/s在路面附著系數為0.5的濕滑瀝青道路上行駛，對車輛施加如圖4所示的正弦前輪轉向角度，同時，為保證車輛的初始行駛速度及車輛模型的線性特性，主動差速器的輸入轉矩設定為86N·m，分別比較有主動差速器(圖中AD曲線)和無主動差速器(圖中OD曲線)工況下的控制力矩及車輛動力學響應特性，如圖5～圖7所示。

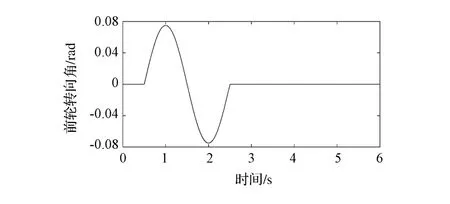
圖4 車輛前輪轉向角度

對于沒有裝備主動差速器的車輛而言，由于濕滑瀝青路面的附著系數相對較低，當施加如圖4所示的前輪轉向角度時，車輛的前、后車輪側偏角會快速增大，導致輪胎的非線性橫向力很快達到其極限值(如圖5所示)，難以為車輛轉向提供所需的橫擺力矩，其橫擺角速度和車身側偏角也會超過其極限值(如圖6所示)。雖然經過3s之后車輛能夠恢復穩定行駛狀態，但在車輛的非穩態行駛過程中容易發生側滑等問題，其安全性能難以得到保證。

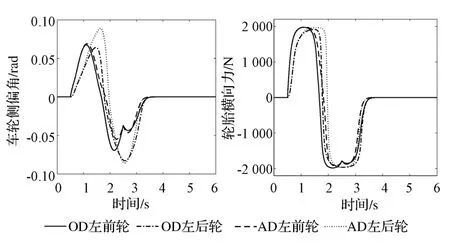
圖5 前、后車輪側偏角及橫向輪胎力

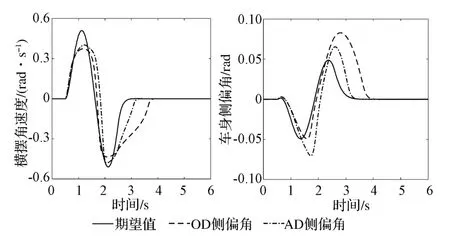
圖6 車輛的橫擺角速度及車身側偏角

另外，從圖7所示的車輛后軸驅動輪的滑移率及輪胎力變化情況可以看出，驅動輪在該工況下的最大滑移率為0.5%，遠未達到10%的非穩態飽和值，其最大驅動力為594N，始終小于輪胎的最大縱向力1 565N(該值由輪胎力的非線性特性分析得到)。因此，可利用主動差速器對左、右兩側輪胎的驅動力矩進行主動分配，并通過差速驅動的方式產生補償橫擺力矩，進而提高車輛的操縱穩定性。

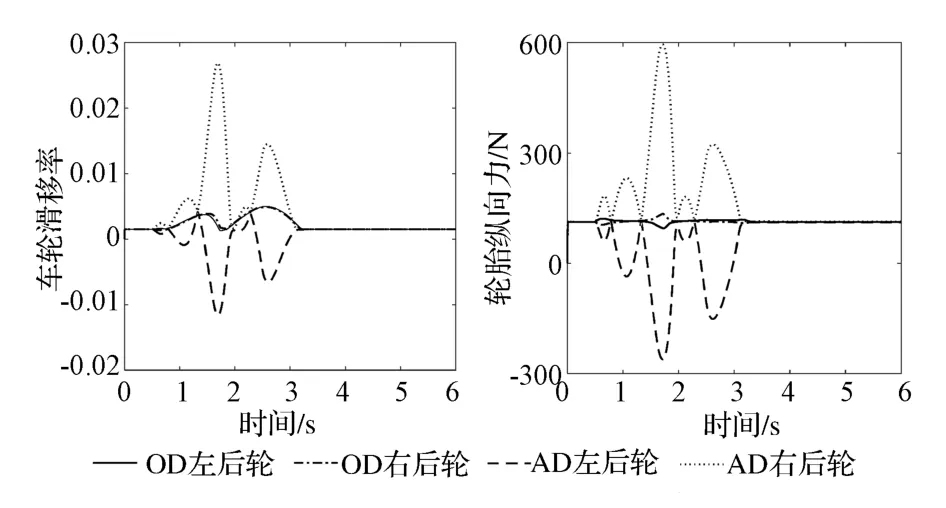
圖7 后軸驅動輪滑移率及縱向力

而對于裝備了主動差速器的車輛而言，當車輛的橫擺角速度和車身側偏角達到約束值時，文中設計的模型預測算法將會計算出期望的補償橫擺力矩，并根據主動差速器動力學特性，得到主動差速器左、右兩側制動器的控制力矩(如圖8所示)，實現后軸上驅動力矩的橫向轉移和主動分配，進而使車輛的橫擺角速度和車身側偏角限定在最大極限值范圍內，有效提高車輛的操縱穩定性。

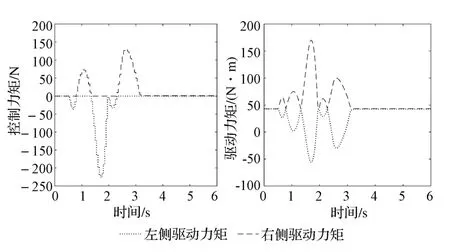
圖8 主動差速器控制力矩及后軸左右兩側驅動力矩

從仿真結果可以看出，利用車輛主動差速器產生補償橫擺力矩時，輪胎的最大縱向滑移率能夠達到0.025，有效增大了輪胎縱向力的利用區域，同時保證了輪胎的縱向力始終處于線性范圍內(滑移率小于0.1)。當車輛在濕滑瀝青路上行駛時，雖然作用于主動差速器上的控制力矩會造成驅動力矩的部分損失，但車輛的行駛速度僅降低至19.34m/s，即僅降低3.3%(如圖9所示)，表明主動差速器對車輛動力性的影響相對較小。

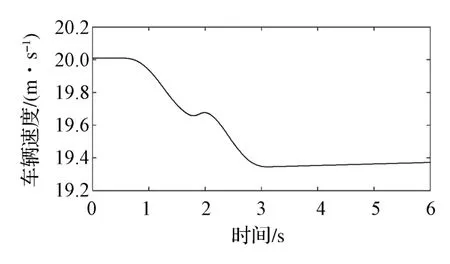
圖9 被控車輛的行駛速度

4 結論

(1)提出的操縱穩定性模型預測算法基于線性車輛動力學模型進行狀態預測，并對控制力矩、輸出狀態等多約束條件進行了分析，克服了單一線性預測模型匹配度差以及非線性預測模型計算量過大的問題。

(2)基于主動差速器的車輛操縱穩定性控制方法增大了驅動車輪在線性穩態區域內的縱向力利用范圍，同時解決了傳統差速制動穩定性控制造成的動力性能損失過大的問題。

(3)本研究僅對恒定速度的線性車輛動力學預測模型進行了研究，在進一步工作中，將充分考慮被控車輛的速度變化、輪胎力的非線性特性等影響因素，構建時變的模型預測控制系統并通過實車道路實驗進一步驗證其系統性能。

[1] ABE Masato.Vehicle handling dynamics:theory and application[M].Oxford:Butterworth-Heinemann，2015.

[2] HANCOCK M J， WILLIAMS R A， FINA E， et al.Yaw motion control via active differentials[J].Transactions of the Institute of Measurement and Control， 2007， 29(2):137-157.

[3] CANALE M，FAGIANO L.Comparing rear wheel steering and rear active differential approaches to vehicle yaw control[J].Vehicle System Dynamics， 2010， 48(5):529-546.

[4] HANCOCK M J， WILLIAMS R A， GORDON T J， et al.A comparison of braking and differential control of road vehicle yaw-sideslip dynamics[J].Proceedings of the Institution of Mechanical Engineers， Part D:Journal of Automobile Engineering， 2005， 219(3):309-327.

[5] 冀杰，李以農，陳翀.車輛主動差速器轉矩橫向傳遞及動力性能分析[J].機械科學與技術，2014，33(1):117-121.

[6] CANALE M，FAGIANOL，FERRARA A，et al.Vehicle yaw control via second-order sliding-mode technique[J].IEEE Transactions on Industrial Electronics， 2008， 55(11):3908-3916.

[7] DEL Re L， ALLGOWERll F， GLIELMO L， et al.Automotive model predictive control:models，methods and applications[M].London:Springer，2010.

[8] WONG A，KASINATHAN D，KHAJEPOUR A，et al.Integrated torque vectoring and power management framework for electric vehicles[J].Control Engineering Practice， 2016， 48:22-36.

[9] DE NOVELLISL，SORNIOTTIA，GRUBER P.Wheel torque distribution criteria for electric vehicles with torque-vectoring differentials[J].IEEE Transactions on Vehicular Technology， 2014， 63(4):1593-1602.

[10] SAWASE K，INOUNE K.Maximum acceptable differential speed ratio of lateral torque-vectoring differentials for vehicles[J].Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering， 2009， 223(8):967-978.

[11] 龔建偉，姜巖，徐威.無人駕駛車輛模型預測控制[M].北京:北京理工大學出版社，2014.

[12] WANG L P.Model predictive control system design and implementation using MATLAB[M].London:Springer，2009.

[13] RUBIN D，AROGETISA.Vehicle yaw stability control using active limited-slip differential via model predictive control methods[J].Vehicle System Dynamics， 2015， 53(9):1315-1330.

[14] ZHANG Y.Solving large-scale linear programs by interior-point methods under the Matlabenvironment[J].Optimization Methods and Software， 1998， 10(1):1-31.

[15] 冀杰.基于自動駕駛系統的車輛縱橫向運動綜合控制研究[D].重慶:重慶大學，2010.