FMCW雷達周期非線性相位估計與矯正

李公全, 賴 濤, 靳 科, 趙擁軍

(信息工程大學導航與空天目標工程學院, 河南 鄭州 450001)

0 引 言

調頻連續波(frequency modulated continuous wave,FMCW)雷達相對脈沖體制雷達具有體積小重量輕,結構簡單,成本低,低截獲概率等優點,因此FMCW雷達在近距離安全檢測、機場異物識別、形變測量等領域具有廣泛的應用[1-4]。而FMCW雷達發射信號的非線性失真嚴重制約其性能,尤其在解線頻調接收機制下,FMCW信號的非線性問題使目標回波能量大范圍擴散,嚴重惡化距離分辨率[5],并且信號回波的時延越大,非線性誤差對系統的影響越大。

由于硬件矯正電路穩定性差,調試周期長,因此信號處理矯正方法憑借其通用性、移植性強的特點以及矯正精度高的優勢,得到研究者的青睞。通常可以將非線性相位建模為多項式相位、周期相位、隨機相位三類,實際雷達系統中這3類相位均存在,只是比重各有差異。針對多項式相位誤差的矯正,文獻[6]采用高階模糊函數(high-order ambiguity function, HAF)估計多項式系數,然后利用重采樣方法對非線性誤差進行矯正,具有較強的工程應用性。文獻[7]綜合利用匹配信號變換及頻譜聚集度實現多項式系數的最大似然估計與非線性矯正,具有良好的抗噪性能,在實際雷達系統中得到了很好的應用。

相比多項式相位,周期相位在非線性相位中處于從屬地位。在多項式相位矯正后,距離壓縮圖像的旁瓣一般都能得到較大程度抑制,但是在漢明加窗距離壓縮的情況下(在實際雷達信號處理中非常有必要),由周期非線性引起的成對回波凸顯出來,嚴重影響距離壓縮質量。因此為獲得更高質量的距離壓縮效果,周期相位誤差的估計與矯正是非常有必要的。目前,針對周期相位誤差矯正的研究還較少,文獻[8]對產生周期相位誤差的因素進行了分析,比如直接數字式頻率合成器(direct digital synthesizer,DDS)本身的雜散、DDS時鐘雜散以及供電電壓雜散,但并沒有提出矯正方法。文獻[9]在直接采樣條件下對發射信號采用三階正弦擬合對周期相位進行了矯正,但是在寬帶條件下很難實現直接采樣,同時估計階數較低,對周期相位誤差補償效果有限,有較多的殘余成對回波無法消除。

隨著系統帶寬提高,FMCW雷達大多采用Dechirp接收以實現低采樣率回波采集,從而使得發射非線性與接收非線性耦合,產生了空變效應,增大了估計以及矯正的難度。本文在寬帶FMCW雷達Dechirp接收體制下,把多項式非線性矯正后的剩余非線性相位建模為多周期正弦分量之和,剖析了周期相位誤差對距離壓縮的影響,著重研究了多分量正弦調頻非線性的參數估計以及矯正問題,提出了匹配初值與非線性最小二乘相結合的參數估計方法,將信號相位變換到頻域后利用峰值搜索獲得調制頻率的估計,進而構造匹配函數,通過一維相位搜索同時估計出幅度以及初相,并以此為初值,利用非線性最小二乘進一步提高估計精度,最后利用匹配傅里葉變換(match Fourier transform,MFT)[10]進行空變非線性矯正。在參數初值估計時僅采用了傅里葉變換及一維相位搜索,能夠快速獲得參數初值的估計結果,克服了多分量正弦參數估計時由于初值選取偏離實際值較大而造成非線性最小二乘難以快速收斂的困難。仿真結果證明了算法的可行性,蒙特卡羅仿真表明隨著信噪比提高,參數估計性能逼近克拉美羅下界。對X波段寬帶FMCW雷達實測數據的處理結果表明,所提算法能夠有效抑制成對回波,顯著提高峰值旁瓣比,得到更好的一維距離像壓縮效果。

1 差頻信號相位誤差分析

1.1 差頻信號模型

存在非線性誤差的FMCW發射信號可以寫為

(1)

式中,fc為載波頻率;K為調頻率;ε(t)為調頻非線性誤差項。

經過一定時延之后,理想點目標的接收信號為

(2)

則Dechirp接收之后信號形式變為

(3)

式中,相位第2項包含了目標的距離信息,通過傅里葉變換可以在頻譜上進行精確估計；第3項為殘余時頻相位項(residual video phase, RVP)[11]。在近場成像時,時延很小,RVP項可以忽略,同時誤差可以近似為導數與時延的乘積,此時中頻信號可以寫為

sif(t)=exp{j2π[fcτ+Ktτ+ε′(t)τ]}

(4)

因此，差頻信號的相位誤差與目標和雷達之間的距離有關,即誤差存在空變性。

根據HAF矯正算法[6],可以將誤差信號建模為多項式集合:

(5)

式中,L為多項式階數,通常取5～7階。

則中頻信號可以進一步表示為

(6)

式中,α1=K。

經過HAF算法矯正之后的信號去除了多項式相位誤差,但是仍然可能存在周期誤差分量,造成主瓣兩邊對稱的成對回波,第3.2節的實測數據處理也驗證了這種觀點,對剩余誤差做FFT時可以看到存在若干尖峰。

下面將從匹配濾波脈沖壓縮的角度進行更深入地討論和研究周期相位誤差對一維距離像的影響。

1.2 周期相位誤差的特性及影響

為方便分析,假定周期相位誤差為單頻正弦信號,則中頻信號可以表示為

sif(t)=exp{j2π[fcτ+Ktτ+Aeτsin(2πfet+θe)]}

(7)

式中,Ae單頻正弦相位誤差的幅度;fe為單頻正弦相位誤差的頻率;θe為單頻正弦相位誤差的初相。

假設理想的FMCW信號通過匹配濾波器后的輸出信號為so(t),則存在單頻周期失真時,匹配濾波后的輸出信號[12]為

som(t)=J0(Aeτ)Env[so(t)]·cos(2πfct)+

cos[(2πfc+nπfe)t+nθe]+

(8)

式中,Jn(Aeτ)為n階第一類貝塞爾函數;Env(·) 為取信號包絡。

cos[(2πfc-πfe)t-θe]}

(9)

而實際場景中周期相位誤差為多個正弦信號之和,即

(10)

這時,成對回波不再僅僅是上述簡單情況的疊加,而且還應加上相互作用的交叉項。但是,由于高次項往往很小,故在很多場合可以忽略不計,此時前面的分析結果依然適用。匹配濾波輸出端的成對回波相當于壓縮波形的旁瓣,會降低峰值旁瓣比,對于合成孔徑雷達(synthetic aperture radar, SAR)來說將造成虛假目標,同時造成成像時的鬼影,因此非常有必要對周期相位誤差信號進行估計與矯正。

2 周期相位誤差的估計與矯正

在實際處理時,由于延遲線數據最為純凈,更能反映系統的非線性,在進行系統參數估計時也更加準確,因此首先使用延遲線數據對系統周期相位誤差各參數進行估計。

由以上分析可知,能夠將差頻信號的相位誤差進一步建模為多項式相位集合與正弦函數集合的和，即

sif(t)=exp{j2π[fcτref+Ktτref+

(11)

式中,M為正弦周期相位的階數;τref為延遲線時延。

去除多項式相位之后剩余信號

(12)

取此時信號的相位并解纏繞:

(13)

為了簡化,式(13)可以進一步寫為

(14)

式中,Bm=2πAmτref；ζ=2πfcτref。需要說明的是,由于延遲線時延τref不準確,ζ為一未知數,但可以將ζ看作常數,并不會影響后續正弦參數的估計。

非線性最小二乘參數估計是當前應用較廣泛的參數估計算法[13],可以有效解決本文模型中的參數估計問題,但是參數初值的選取將直接影響最小二乘的收斂速度以及陷入局部最優解的概率。在多階周期誤差信號的參數估計上,需要估計的參數數量很大,因此在參數初值的選取上不能夠隨意指定。

2.1 基于頻率相位匹配的參數初值估計

(15)

式中,θ∈(-π,π),為待估計相位。

將匹配函數與誤差信號相乘,即

χm(t)=φm(t)·γm(t)=

(16)

式中，φj(t)為誤差相位;初始為φ1(t)=φ(t)。

令m=m+1,更新誤差相位,即

(17)

重復以上步驟,直到估計出M個正弦分量的參數值。

基于頻率相位匹配的參數估計方法可以很快速的獲得各個正弦分量的幅度,頻率以及初相的初步估計值,雖然在估計的過程中存在誤差傳遞以及估計不夠準確的問題,但是用其作為非線性最小二乘估計的初值卻是十分方便以及快捷的。

2.2 基于非線性最小二乘的多分量正弦信號參數估計

針對粗略估計的參數初值,仍然需要進行更加精確的優化,使估計值更加接近真實值,通過構建優化目標函數,非線性最小二乘算法可以快速完成這一優化過程。

在本模型中,令

φdata(t)

(18)

式中,b=(B1,B2,…,BM);ω=(ω1,ω2,…,ωM);θ=(θ1,θ2,…,θM);φdata(t)為相位數據。

因此,非線性最小二乘目標函數可以表示為

(19)

將式(18)代入式(19)得

φdata(t)]·

(20)

函數ξ(b,ω,θ)的極值點(b*,ω*,θ*)就是最小二乘解,即

(21)

在非線性最小二乘求解時,可以采用經典的信賴域優化算法[14]。將ξ(b,ω,θ)在當前點(b,ω,θ)(k)處泰勒展開到二次項:

Qk(d)=ξ[(b,ω,θ)(k)]+[g(k)]Td+

(22)

式中,g(k)和Gk分別是ξ(b,ω,θ)在(b,ω,θ)(k)處的梯度向量以及Hesse矩陣;d(k)是Qk(d)的最小點。

信賴域算法的主要思想就是在(b,ω,θ)(k)的鄰域內用Qk(d)的極小解近似ξ(b,ω,θ)并令(b,ω,θ)(k+1)=(b,ω,θ)(k)+d(k)作為ξ(b,ω,θ)極小解新的近似不斷重復。其中d(k)的求解問題通常叫做信賴域子問題,即解下式:

minQk(d)

s.t. ‖d‖≤hk

(23)

記

(24)

它們的比值

(25)

當ξ(b,ω,θ)為二次函數時rk等于1,對于一般函數,rk越接近于1表示在(b,ω,θ)(k)的這個鄰域內Qk(d)近似ξ(b,ω,θ)程度越高,因此以rk作為衡量近似程度的指標。

則信賴域方法的計算步驟如下[15]。

步驟1給定初始值(b,ω,θ)(1),初始半徑h1,迭代終止誤差μ,令k=1。

步驟3求式(23)的解,計算ξ[(b,ω,θ)(k)+d(k)]及rk,轉步驟4。

步驟4若rk<β1,令hk+1=β2∥d(k)∥;若rk>β3及∥d(k)∥=hk,此時令hk+1=β4hk;否則令hk+1=hk。

步驟5若rk≤0,則令(b,ω,θ)(k+1)=(b,ω,θ)(k);否則令(b,ω,θ)(k+1)=(b,ω,θ)(k)+d(k),k=k+1,轉到步驟2。

根據經驗,可取信賴域法中參數β1=0.25,β2=0.25,β3=0.75,β4=2。

2.3 非線性矯正MFT算法

MFT[10,16]的一般形式為

(26)

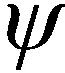
含正弦周期相位誤差的多目標差頻信號可表示為

(27)

式中,P為目標數;τp為第p個目標的回波時延。

其傅里葉變換為

(28)

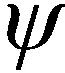
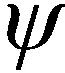
(29)

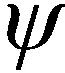
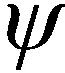
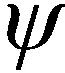
(30)

可見,雖然估計出的Bm含有延遲τref,但是由文獻[6]可知,在進行多項式系數估計時,Kτref作為一個整體被估計出來,因此在實際進行周期誤差矯正時τref被消除掉,即式(30)與τref值無關,并不需要知道系統延遲線τref的精確值。

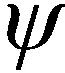
綜上,整個非線性矯正的流程如圖1所示。

圖1 非線性矯正流程Fig.1 Nonlinearity correction process

3 仿真實測驗證

為驗證算法的有效性,進行了仿真以及實測數據驗證。本節主要包含兩部分,第一部分進行含周期相位誤差信號的單目標以及多目標一維距離向成像,同時對不同信噪比下算法的估計性能進行了仿真分析;第二部分對實際系統的延遲線以及角反射器數據進行周期誤差的非線性矯正,顯示算法在實際系統中的應用效果,證明了算法的工程實用性。

3.1 仿真驗證

根據實際系統的參數,設置了仿真模擬的系統參數如表1所示。

首先,對10 m處的模擬點目標進行仿真矯正。系統采用三階周期相位誤差,矯正前后的一維距離像結果如圖2所示。從圖中可以看出,周期相位調制并不會影響系統的分辨率,但是在旁瓣結構上會出現嚴重的成對回波,降低了峰值旁瓣比,將會掩蓋對遠區弱目標的探測。經過對周期相位誤差的矯正,旁瓣電平由-20 dB降低到約-39 dB,接近理想情況。

表1 寬帶FMCW雷達系統參數

然后,將估計出的參數對位于15 m以及16 m的兩個點目標進行矯正,矯正前后結果如圖所示,可以看到與單個點目標的旁瓣抑制效果基本一致。

圖2 非線性矯正仿真結果Fig.2 Simulation results of nonlinearity correction

上述仿真是在理想環境下進行的,為了評估算法的普適性,我們對不同信噪比條件下的估計性能進行了蒙特卡羅數值仿真。

文獻[17]已經給出了正弦調頻幅度和頻率CRLB的詳細推導過程,在此基礎上進一步推導出初相的CRLB,鑒于推導過程基本類似且篇幅較長,在此只給出推導結果為

(31)

式中,N為信號長度。

由于多分量正弦調制相位的參數估計與單分量參數估計在估計性能上沒有本質區別,只是計算復雜度更高一些,因此為方便起見,我們對只單分量正弦調制相位的參數估計性能進行分析即可。信噪比從5 dB到20 dB變化,采用100次蒙特卡羅數值仿真實驗,分別計算調制相位的幅度,頻率以及初相的歸一化均方根誤差(normalized mean square error, NRMSE),圖3顯示出本算法的估計性能。

圖3 調頻參數估計性能分析Fig.3 Estimation performance analysis

由圖3可知,由于匹配初值估計是基于頻譜的估計,因此受限于頻率間隔以及相位搜索的步長,非線性最小二乘顯著提高了參數估計精度。由于本算法是基于取相位的參數估計,因此存在8 dB的信噪比門限,但是在信噪比大于8 dB時本算法估計參數的NRMSE逼近CRLB。

3.2 實測數據驗證

為了體現本算法的實際應用效果,我們利用實驗室研制的超寬帶FMCW雷達系統實測數據進行驗證,雷達參數如表1所示,系統結構框圖可參考文獻[18]。首先根據系統延遲線數據對系統的周期相位誤差參數進行估計,然后再對實際場景的回波進行矯正。因此在本算法應用時,只需在原系統上加裝一條延遲線即可,并不會過多增加系統的復雜性。系統實景測試如圖4所示。

圖4 實測場景圖Fig.4 Field survey scenario

根據算法的具體實現過程,通過約3 m的延遲線回波數據對相位誤差參數進行了估計,之后對位于約4.93 m的角反射器回波數據進行矯正。首先用高階模糊函數法矯正信號中多項式非線性相位的影響,在回波沒有加Hamming窗時,看似信號達到了我們所需求,如圖5(a)所示;但是加入Hamming窗后,主瓣兩旁的成對回波凸顯出來,且峰值旁瓣比僅有21 dB,如圖5(b)所示,這些成對回波對周圍目標有很強的掩蓋效應,遠遠不能滿足我們對信號檢測的要求,因此迫切需要矯正這些周期性相位誤差。對多項式相位矯正之后的殘余相位誤差做傅里葉變換以觀察其頻譜,如圖5(c)所示,從中可以看出殘余相位頻譜中具有明顯的周期性相位誤差,表現出多個尖峰,這種情況下僅如文獻[9]采用3階正弦函數擬合是不夠的。

應用本文算法對多項式相位矯正之后的數據繼續矯正,圖6分別為延遲線與角反射器回波矯正結果。從圖5(c)的殘差頻譜圖中粗略看到了7個頻率譜峰,在實際處理時,為顯示更多細節頻率成分以及降低因某個頻率估計不準造成非線性最小二乘優化過程收斂較慢,同時兼顧數據處理的運算效率,在本文中采用9階正弦對延遲線回波數據中的周期相位誤差進行估計。同時,由于系統穩定性良好,在實際參數估計時,只需根據一個延遲線脈沖數據對參數進行估計即可對其他脈沖或者其他場景回波數據進行矯正。

圖5 多項式誤差矯正結果Fig.5 Results of polynomial nonlinearity correction

從圖6中可以看出,算法在多項式矯正結果的基礎上仍然能夠將延遲線數據一維距離像旁瓣壓縮9 dB左右,顯著抑制了成對回波,同時矯正后距離分辨率為3.85 cm,接近3.82 cm的理想分辨率。由于實際場景的復雜性,對角反射器數據的矯正結果雖然不如延遲線數據的矯正結果優越,但仍能將旁瓣抑制7～8 dB,距離分辨率也得到了較大改善,能夠有效提升對目標的檢測與成像效果,顯示了本算法良好的工程應用性。延遲線和角反射器矯正前后詳細指標如表2所示。

圖6 實測數據周期相位誤差矯正結果對比Fig.6 Field survey results of nonlinearity correction

性能指標延遲線角反射器最高旁瓣電平/dB矯正前-20．67-17．46矯正后-29．44-25．023dB分辨率/cm矯正前3．874．42矯正后3．853．91

但是,從圖6(b)也可以看出,雖然近處旁瓣得到了較好的抑制,但是仍然存在沒有估計消除的遠區旁瓣。這一點解釋為地板下可能存在的強散射體,圖中黑色實線是無角反射器存在時對環境的成像結果,在約4.45 m以及5.40 m的位置同樣出現較強的反射,從側面驗證了上述結論。當然,在實際應用中,鑒于正弦估計的階數有限,也可能產生類似的遠區旁瓣。

4 結 論

本文主要研究了FMCW信號周期非線性誤差的參數估計與矯正問題。文章首先分析了距離壓縮中由周期非線性誤差引起的成對回波現象,然后針對周期相位誤差的參數估計問題,采用頻率相位匹配對參數的初值進行估計,之后為提高參數估計性能,采用了信賴域算法對估計出的初值進行優化,最后通過MFT對誤差進行矯正。仿真以及實測數據均表明本文算法能夠準確估計周期相位誤差參數,顯著抑制成對回波效應,提高對目標的檢測和成像效果,具有良好的工程應用性。

[1] POHL N, JAESCHKE T, VOGT M. Ultra high resolution SAR imaging using an 80 GHz FMCW-radar with 25 GHz bandwidth[C]∥Proc.of the European Conference on Synthetic Aperture Radar, 2012:189-192.

[2] IGLESIAS R, AGUASCA A, FABREGAS X, et al. Ground-based polarimetric SAR interferometry for the monitoring of terrain displacement phenomena-Part I: theoretical description[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(3):980-993.

[3] MOLCHANOV P, GUPTA S, KIM K, et al. Short-range FMCW monopulse radar for hand-gesture sensing[C]∥Proc.of the IEEE Radar Conference, 2015:1491-1496.

[4] YAN J B, ALVESTEGUI G G, MCDANIEL J W, et al. Ultrawideband FMCW radar for airborne measurements of snow over sea ice and land[J]. IEEE Trans.on Geoscience & Remote Sensing, 2016, PP(99):1-10.

[5] WANG Y, LI Q, GAN D, et al. Research on nonlinearity correction imaging algorithm of FMCW SAR[C]∥Proc.of the International Conference on Signal Processing Systems, 2010:V1-425-V1-429.

[6] ANGHEL A, VASILE G, CACOVEANU R, et al. Short-range wideband FMCW radar for millimetric displacement measurements[J].IEEE Trans.on Geoscience & Remote Sensing, 2014, 52(9):5633-5642.

[7] ANGHEL A, VASILE G, CACOVEANU R, et al. Range autofocusing for FMCW radars using time warping and a spectral concentration measure[C]∥Proc.of the IEEE Radar Conference, 2015:0581-0586.

[8] AYHAN S, SCHERR S, BHUTANI A, et al. Impact of frequency ramp nonlinearity, phase noise, and SNR on FMCW radar accuracy[J]. IEEE Trans.on Microwave Theory & Techniques, 2016, 64(10):1-12.

[9] 趙志勇, 常文革, 黎向陽,等. 去調頻處理中空變相位誤差補償方法[J]. 國防科技大學學報, 2014(3):169-176.

ZHAO Z Y, CHANG W G, LI X Y, et al. Range-dependent phase error compensation of dechirp[J].Journal of National University of Defense Technology, 2014(3):169-176.

[10] 王盛利, 李士國, 倪晉麟,等. 一種新的變換——匹配傅里葉變換[J]. 電子學報, 2001, 29(3):403-405.

WANG S L, LI S G, NI J L, et al. A new transform—match Fourier transform[J]. Acta Electronica Sinica, 2001, 29(3): 403-405.

[11] MITTERMAYER J, MOREIRA A, LOFFELD O. Spotlight SAR data processing using the frequency scaling algorithm[J]. IEEE Trans.on Geoscience & Remote Sensing, 1999, 37(5):2198-2214.

[12] HU S. Performance analysis of frequency sweep nonlinearities in LFM radars[C]∥Proc.of the IEEE International Conference on Electrical and Control Engineering,2010:3977-3980.

[13] ANGEBY J. Estimating signal parameters using the nonlinear instantaneous least squares approach[M]. IEEE Press, 2000.

[14] 賴炎連,賀國平.最優化方法[M].北京:清華大學出版社,2008.

LAI Y L, HE G P. Optimization methods[M]. Beijing:Tsinghua University Press, 2008.

[15] 謝政, 李建平, 陳摯. 非線性最優化理論與方法[M]. 北京:高等教育出版社, 2010: 194-199.

XIE Z, LI J P, CHEN Z.Nonlinear optimization theory and methods[M].Beijing:Higher Education Press,2010:194-199.

[16] CHEN J J, CHEN J, WANG S L. Detection of ultra-high speed moving target based on matched Fourier transform[C]∥Proc.of the IEEE International Conference on Radar, 2006:1-4.

[17] 霍凱, 游鵬, 姜衛東,等. 正弦調制相位信號參數估計的克拉美-羅下限[J]. 信號處理, 2009, 25(9):1342-1346.

HUO K,YOU P,JIANG W D, et al. The Cramer-Rao lower bound for parameters estimation of signals with sinusoid modulated phase[J]. Signal Processing, 2009, 25(9):1342-1346.

[18] 靳科, 賴濤, 李公全,等. 近距離超寬帶調頻連續波雷達非線性校正研究[J]. 信號處理, 2017,33(2):158-167.

JIN K, LAI T, LI G Q, et al. Nonlinearity correction of short range wideband FMCW radar[J]. Signal Processing,2017,33(2):158-167.