基于猶豫模糊集統計相關系數的多源異類數據融合識別
關 欣, 孫貴東, 衣 曉, 趙 靜
(海軍航空大學電子信息工程系, 山東 煙臺 264001)
0 引 言
多傳感器多源數據識別是根據各傳感器上報的帶有不確定性的身份信息需要進一步進行融合處理,給出量測目標身份判斷的過程。實際上是對量測信息進行分類與處理的過程,給出量測目標的類別與屬性。在融合識別問題中由于屬性的差異性,導致描述方法往往不一致,有的屬性傾向于用定量數據表示,而有的更適合用定性概念描述,產生了多源異類數據融合識別的問題。文獻[1]指出數據融合的數據往往是處理描述同一現象的多源異類信息。由于數據源的多源異類性,往往導致融合識別的不確定性。而模糊集作為不確定性處理的一種重要手段,自文獻[2]提出其概念來,經過半個多世紀的發展,相繼產生了區間模糊集、二型模糊集、模糊多重集、直覺模糊集、猶豫模糊集等多種樣式的模糊集,并且在多源異類數據融合領域得到了應用。文獻[3]研究了實數、區間數、三角模糊數、直覺模糊數和語義變量組成的混合多屬性決策問題,通過將混合數據統一到區間框架內進行多屬性決策。文獻[4]研究了實數、區間數、語義變量、直覺模糊數、猶豫模糊數和猶豫模糊標簽組成的多源異類多屬性群決策問題,并基于TOPSIS方法進行多屬性決策判定。文獻[5-7]則分別基于直覺模糊集、區間直覺模糊集數學規劃方法,研究了具有直覺模糊信度和區間直覺模糊信度的區間直覺模糊數、直覺模糊數、三角模糊數、語義變量、區間數和實數組成的混合多屬性決策問題,并采用逼近理想解的方法進行決策判定。盡管上述文獻較好地處理了多源異類數據的決策問題,但是其框架主要是基于區間數和直覺模糊數討論的,而猶豫模糊集作為新概念,2010年由文獻[8-9]提出,相比其他模糊集,在確定隸屬度函數時,不像2-型模糊集的隸屬度為概率分布,也不像區間模糊集和直覺模糊集由不確定誤差幅度確定隸屬度,是因為隸屬度的取值有一系列可能值。由于其隸屬度是在[0,1]內猶豫不定,更能符合多源異類數據融合時各傳感器上報的獨立決策不確定性,因此基于猶豫模糊集描述多源異類數據來對多源異類數據的融合識別進行研究。
相關分析是衡量兩個變量之間線性接近程度的重要方法,關于猶豫模糊集相關系數的研究目前也有許多進展。文獻[10]首先定義了5種猶豫模糊數(hesitant fuzzy element,HFE)的相關系數,將其應用到醫療診斷領域。在此基礎上,文獻[11]提出了猶豫模糊集(hesitant fuzzy sets,HFS)相關系數,并解決聚類問題。文獻[12]分析了現有相關系數的不足,提出了新的相關系數,在醫療診斷、聚類分析問題中得到了應用。文獻[13-19]又分別將相關系數拓展到區間猶豫模糊集、二重猶豫模糊集、區間二重猶豫模糊集和猶豫語義標簽集領域,并在特征提取、模式識別、多屬性決策、聚類分析、水質評估和醫療診斷等領域具體應用。盡管上述文獻提出了幾種HFS相關系數,也在多個領域得到了應用,但是都存在不足。文獻[10]中5種定義方法僅限于計算HFE的相關系數。文獻[11]的定義雖然可以計算HFS的相關系數,但是其定義不符合統計學直覺,并且需要各HFE中隸屬度個數相同。文獻[12]的定義雖然符合統計學直覺,但相關定義過程中的數學概念存在爭議。并且目前還沒有以猶豫模糊集為框架的基于其相關系數的多源異類數據融合方法。
本文試圖基于猶豫模糊集框架,解決多源異類數據的融合識別問題,主要討論猶豫模糊數HFE、直覺模糊數IFN、區間數和實數4類基本數據組成的多源異類數據。首先將多源異類數據猶豫模糊描述以統一進行相關分析,其次在現有HFS相關系數基礎上,提出HFS統計相關系數,使其既滿足統計學直覺,又不需要各HFE中隸屬度個數相同,并且修正了相關系數定義過程中數學概念不明確的問題,考慮實際問題中屬性權重的影響將其拓展為加權HFS相關系數,最后利用所提出的HFS統計相關系數解決多源異類數據的融合識別問題。
1 猶豫模糊集描述
記論域X={x1,x2,…,xn},則X上的猶豫模糊集(hesitant fuzzy sets, HFS)定義[8-9]為
M={[x,hM(x)]|x∈X}
(1)
式中,hM(x)為猶豫模糊數(hesitant fuzzy element,HFE),由一系列[0,1]內的不同數值組成,描述集合X中元素x對M的隸屬度,有時候也稱M為HFE,即HFES,HFES與HFS實際上是等價的,文中統一用HFS表示。
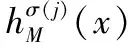
文獻[8-9]提出猶豫模糊數包絡的概念,用來表示直覺模糊數。對于X上的猶豫模糊數h(x),簡記為h,γ為h中隸屬度可能值,即γ∈h(x),表示為
μ=h-,h-=min{γ|γ∈h}
(2)
υ=1-h+,h+=max{γ|γ∈h}
(3)
猶豫模糊數的包絡可以用直覺模糊數(μ,υ)表示,記為Aenv(h)。
文獻[23-24]定義了猶豫模糊數的記分函數和方差來比較猶豫模糊數。對于猶豫模糊數h,其記分函數和方差為
(4)
(5)
式中,l(h)為h中元素的個數;γ∈h(x)。則對于兩個猶豫模糊數h1和h2有
(1) 如果s(h1)>s(h2),則h1>h2。
(2) 如果s(h1)=s(h2),那么
滿足v(h1)>v(h2),則h1 滿足v(h1)=v(h2),則h1=h2。 記X上猶豫模糊數h(x)、直覺模糊數A(x)、區間數I(x)和實數R(x)分別為 (6) 式中,γ為h(x)的隸屬度;u、v分別為A(x)的隸屬度和非隸屬度,且0≤u+v≤1;a-、a+分別為I(x)的下界和上界。 式(2)和式(3)將h(x)用A(x)表示,同理也可以將A(x)用h(x)表示[8-9],即對于給定的猶豫模糊數A(x)=〈u,v〉,可以將其用猶豫模糊數表示為 A(x)→h(x)={u,1-v} (7) 而直覺模糊數A(x)和區間數I(x)之間關系為 I(x)→A(x)={a-,1-a+} (8) 則可以用猶豫模糊數h(x)將區間數I(x)表示為 I(x)→h(x)={a-,a+} (9) 而實數R(x)的猶豫模糊數h(x)為 I(x)→h(x)={a} (10) 通過式(7)~式(10)實現將猶豫模糊數h(x)、直覺模糊數A(x)、區間數I(x)和實數R(x)組成的多源異類數據用猶豫模糊數h(x)統一表示,成功將多源異類數據問題轉化為猶豫模糊集問題。為此,只需討論猶豫模糊數的相關分析即可實現對多源異類數據的融合識別。 現有的猶豫模糊集相關分析方法主要為文獻[10]提出的5種HFE相關系數、文獻[11]提出的2種HFS相關系數以及文獻[12]改進的HFS相關系數。 文獻[10-11]定義的HFS相關系數,忽略了負相關,僅為一種相關的強度,理論上不符合傳統統計學相關系數落于[-1,1]的要求,計算過程需要HFE中隸屬度個數相同。而文獻[12]改進的相關系數實際上僅為一種均值相關。文獻[11]定義的HFS的相關和文獻[12]定義的HFS加權均值、方差和相關均有待商榷,一方面形式上不符合直覺,另一方面不符合數學邏輯定義,存在類似重復等權重系數的問題,方差的定義也不符合統計數學邏輯。 因此,在現有HFS相關系數的基礎上,首先定義HFS的數學概念,修正了現有HFS相關系數及其附屬概念的定義方法,提出HFS統計相關系數,既滿足取值落于[0,1]的統計學要求,又不需要HFE內隸屬度個數相同。 統計學相關系數的定義是歸一化隨機變量的協方差。基于文獻[12]首先定義HFS的均值、方差和協方差。 對于X={x1,x2,…,xn}上的猶豫模糊集M={〈x,hM(x)〉|x∈X},其均值定義為 (11) (12) 在HFS均值的基礎上定義HFS方差為 (13) 在方差的基礎上定義,HFSM和N之間的(互)協方差為 (14) 式中,lMj和lNj分別為HFEhM(xj)和hN(xj)中隸屬度個數,且當M=N時,Cov(M,N)=Var(M,N)。 對于X={x1,x2,…,xn}上的猶豫模糊集M、N,如果算子c(M,N)滿足下列條件: (1)c(M,N)=c(N,M); (2) 當M=N時,c(M,N)=1; (3) -1≤c(M,N)≤1。 則稱c(M,N)為M和N之間的相關系數。 在HFS方差和協方差的基礎上,基于現有HFS相關系數,定義HFS統計相關系數為 (15) 例1給出一個簡單例子進行統計相關系數的計算說明。 記X={x1,x2,…,xn}上的兩個猶豫模糊集M和N分別為 M={〈x1,{0.7,0.5}〉,〈x2,{0.7,0.5,0.4}〉, 〈x3,{0.6,0.4,0.3}〉} N={〈x1,{0.5,0.4,0.2}〉,〈x2,{0.8,0.5}〉, 〈x3,{0.7,0.6,0.3}〉} 首先,計算M、N中各HFE均值分別為 則M、N的均值分別為 利用式(14)計算M、N的協方差、方差分別為 (0.367-0.517)+(0.533-0.522)×(0.65-0.517)+ (0.433-0.522)×(0.533-0.517)]=-0.003 89 (0.533-0.522)2+(0.433-0.522)2]=0.004 71 (0.65-0.517)2+(0.533-0.517)2]=0.013 48 所以,相關系數為 例1表明HFS統計相關系數方法能夠很好處理HFS中和HFE中隸屬度個數不相同的問題,而文獻[10-11]相關系數不能直接處理此類數據,必須通過數值延拓后才能夠處理,不可避免地增加了度量誤差。 (16) (17) (18) 上述定義修正了文獻[12]定義的不足,基于修正后的HFS的數學概念定義加權HFS相關系數為 cw(M,N)= (19) 多源異類數據的識別問題是現實生活中面臨的基本問題,由于屬性的差異性,導致屬性描述的方式往往不一致,具體體現在屬性數據類型的多源異類性,在前文敘述多源異類數據的猶豫模糊統一的基礎上,基于統計HFS相關系數對多源異類數據進行融合識別判定。 記待識別的多屬性多源異類數據集為A={A1,A2,…,Ai,…,An1},每類數據集具有m種屬性P={p1,p2,…,pj,…,pm},其中屬性數據由猶豫模糊數h(x)、直覺模糊數A(x)、區間數I(x)和實數R(x) 4種數據形成多源異類數據屬性。由于多源異類數據之間無法直接融合處理,考慮將其統一到猶豫模糊域后再進行識別判定。為此,基于第2節所述的多源異類數據表述方法,用猶豫模糊數將多源異類數據表示為 (20) 則統一記待識別目標Ai在屬性pj上的多源異類數據的猶豫模糊表示為hAi(pj),則待識別目標Ai在屬性集P上的多源異類數據屬性的猶豫模糊表示為 Ai={〈pj,hAi(pj)〉|pj∈P} (21) 則所有待識別多源異類數據集A的猶豫模糊表示為 A= (22) 式中,1≤i≤n1;1≤j≤m。基于HFS統計相關系數進行進一步識別判定即可。 記現有的目標多屬性猶豫模糊數據庫為B={B1,B2,…,Bk,…,Bn2},同樣每類數據集具有m種屬性P={p1,p2,…,pj,…,pm},其中屬性數據僅由猶豫模糊數h(x)組成。記數據庫數據Bk在屬性pj上的猶豫模糊表示為hBk(pj),則Bk在屬性集P上的猶豫模糊屬性表示為 Bk={[pj,hBk(pj)]|pj∈P} (23) 則數據庫B的猶豫模糊表示為 B= (24) 式中,1≤k≤n2;1≤j≤m。 基于HFS統計相關系數可以計算猶豫模糊表示后的多源異類數據集A和數據庫B之間對應的猶豫模糊數據Ai和Bk之間的相關系數c(Ai,Bk),并在此基礎上得到多源異類數據集A和數據庫B之間的相關系數,兩者分別為 (25) c(A,B)= (26) 式中,i=1,2,…,n1;j=1,2,…,m;k=1,2,…,n2;lAij和lBkj分別為Ai和Bk在屬性pj上對應的HFE的隸屬度個數。 根據多源異類數據集A和數據庫B之間的相關系數c(A,B),即可實現對多源異類數據的識別判定。由于本文研究的重點在于猶豫模糊集統計相關系數,為此這里僅提供一種簡單易實現的識別判定方法,采用最大相關系數識別判定準則 (27) 式中,增加門限ε、η,0.5<ε≤1,η根據相關系數計算區分度而定,如果滿足 (28) 基于HFS統計相關系數的多源異類數據融合識別步驟為: 步驟1確定待識別多源異類數據集A和猶豫模糊數據庫B; 步驟2用猶豫模糊數統一描述多源異類數據集A; 步驟3基于HFS統計相關系數計算猶豫模糊表示后的多源異類數據集A和猶豫模糊數據庫B之間對應數據的相關系數c(Ai,Bk),并形成c(A,B); 步驟4以相關系數c(A,B)作為識別判定指標,采用最大相關系數識別判定準則,如果滿足識別條件,則判定相關系數大的為識別結果。 將所提出的猶豫模糊集數統計相關系數應用到多源異類數據的融合識別問題中。設計了3組算例:①驗證HFS統計相關系數的有效性并與文獻[10]和文獻[12]相關系數進行對比分析;②討論HFS統計相關系數以及權重對識別結果的影響;③用HFS統計相關系數解決多源異類數據的識別問題。 本算例采用經典的醫療診斷識別算例,文獻[10]和文獻[12]均有介紹,一方面驗證HFS統計相關系數識別的有效性,另一方面更好地與文獻[10]和文獻[12]的相關系數進行對比分析。假設診斷癥狀庫內有5類癥狀信息,分別記為R1、R2、R3、R4、R5;每類癥狀具有5種屬性,分別記為p1、p2、p3、p4、p5;屬性描述采用猶豫模糊數表示,現有4位待識別個體,分別記為A1、A2、A3、A4,需要診斷其癥狀。5類HFS癥狀數據庫及4位待識別個體的HFS數據分別如表1、表2所示。 表1 HFS癥狀數據庫 表2 猶豫模糊待識別數據 采用本文提出的HFS統計相關系數(15)計算每位待識別個體與癥狀數據庫之間的相關系數,將其作為識別指標,得到的計算結果如表3所示。 表3 癥狀識別相關系數表 通過表3得知,個體A1,A3,A4分別識別為癥狀R2,而A2識別為癥狀R4,識別結果與文獻[9]中的計算結果一致,驗證了HFS統計相關系數的有效性,并且HFS統計相關系數取值在[0,1]上,克服了文獻[10]、文獻[11]相關系數的不足。為了對比HFS統計相關系數與文獻[10]、文獻[11]相關文獻的識別效果,本文將3種方法計算的結果進行對比,其中HFS統計相關系數與文獻[12]相關系數的對比如圖1所示,與文獻[10]相關系數的對比如圖2所示。3種方法的計算時間對比如表4所示。 圖1 與文獻[12]相關系數計算的識別對比圖Fig.1 Correlation coefficient results compared with [12] 圖2 與文獻[10]相關系數計算的識別對比圖Fig.2 Correlation coefficient results compared with [10] 圖1中虛線表示文獻[12]相關系數的計算效果,實線表示HFS統計相關系數的計算效果,通過圖1的對比分析得知,兩種方法的計算結果相同,但是注意到圖1中各對應實線在0點上方總是位于虛線下方;而在0點下方總是位于虛線上方,表明其對應的相關系數取值的絕對值要小于文獻[12]相關系數的絕對值,并且實線對應最大值與次大值之間的差距要比虛線大,表明HFS統計相關系數變化率要比文獻[12]相關系數的識別變化率靈敏,即HFS統計相關系數在識別區分度上要比文獻[12]相關系數有優勢。 圖2中虛線表示文獻[12]相關系數的計算效果,而實線表示HFS統計相關系數的計算效果,通過圖2的對比分析得知,兩種方法的計算結果有所不同,但是主要問題在于文獻[10]相關系數的取值均為[0,1]內,并且在與HFS統計相關系數相同的圖像框架內,其識別效果近似一條直線,很難區分識別結果,文獻[10]相關系數的計算結果在區分度上比HFS統計相關系數要差。 表4僅給出在計算機處理器為Inter i7 3770K 3.5 GHz、內存8 GB、64位操作系統環境下,使用Matlab軟件對編寫的3種相關系數函數處理時的計算時間,其中不包括后續的作圖處理時間。 表4 相關系數計算時間對比 通過表4得知,3種方法在數據讀取和計算速度的差異不大,盡管本文方法的時間是最長的,但是橫向對比而言,3種方法計算時間都非常快,本文算法增加的計算時間在合理范圍。本文算法計算時間長的原因在于,本文方法在相關系數計算時,采用了最大值遍歷函數,相比其他兩種方法直接乘性和開方計算要多消耗一部分時間,但是消耗的時間與增加計算精度相比而言是可以接受的。 前一節的計算結果是在沒有考慮權重的條件下得到的,但在實際計算過程中,屬性權重對識別結果十分重要。為此采用與算例1相同的算例計算,利用加權HFS相關系數(19)重復上述算例的計算,其中各屬性權重分別設定為0.1、0.2、0.3、0.3、0.1,得到的計算結果如表5所示。 表5 癥狀識別相關系數表 通過表5得知,個體A1、A3分別識別為癥狀R2,A2識別為癥狀R4,但是個體A4的識別結果本例中判定為未識別,即未在癥狀庫中找到個體A4的癥狀。一方面在于其計算相關系數比較低,另一方面相關系數最大值與次大值之間比較接近,因此不能簡單判定識別結果為相關系數最大值對應的癥狀R2,而判為未找到識別結果更為合適。屬性權重的改變導致識別結果發生了變化,為了進一步驗證屬性權重的重要性,仿真設計屬性4的權重從0.1按步長0.2變化到0.9,其余屬性權重平均,利用加權HFS相關系數重新計算上例,并得到個體A4的識別效果隨權重的變化圖如圖3所示,其余個體的識別效果圖可類似給出,這里僅以A4為例分析。 圖3 個體A4的識別效果隨權重的變化圖Fig.3 Recognition effect of A4 with different attribute weights 由圖3得知,個體A4的識別效果隨權重的變化圖而改變,當屬性4權重較小時,可以判定A4的識別結果為癥狀R2,隨著權重的增加,其識別效果越來越不明顯,識別結果在R1和R2之間不易區分,此時記判定為未找到識別結果一類。通過對HFS相關系數屬性權重的分析得知,識別結果會隨著屬性權重的改變而變化,因此實際問題中,在進行加權HFS相關系數的計算時應充分考慮權重的分配,以得到更合理的識別結果。 上例分析了HFS統計相關系數在猶豫模糊集數據域的識別效果,本節將HFS統計相關系數應用到多源異類數據的識別問題中。采用的是猶豫模糊數據庫,如表6所示,具有5類已知目標特征,也分別記為R1、R2、R3、R4、R5;每類目標具有5種屬性,分別記為p1、p2、p3、p4、p5。 表6 猶豫模糊數據庫 而待識別多源異類數據如表7所示,主要由4類待識別目標組成,分別記為A1、A2、A3、A4。每類目標均具有5類屬性信息,并且5類屬性信息分別由實數、區間數、直覺模糊數、猶豫模糊數和這4種數據組成的多源異類數據描述,因此此問題就變成了多源異類數據的識別問題。基于HFS統計相關系數,采用第4節的識別方法對其進行識別判定。 表7 多源異類待識別數據 基于第2節所述的多源異類數據統一方法,將由實數、區間數、直覺模糊數、猶豫模糊數組成的多源異類數據用猶豫模糊數統一表示,并按照降序排列,得到多源異類數據轉化后的猶豫模糊屬性,如表8所示。 表8 多源異類轉化后猶豫模糊待識別數據 采用HFS統計相關系數計算多源異類數據轉化后的猶豫模糊屬性和表5猶豫模糊數據庫之間的相關系數,作為識別指標,得到的計算結果如表9所示。 表9 多源異類數據識別相關系數表 由表9得知,目標A2識別為數據庫中R5,A4識別為數據庫中R3,而目標A1和A3則由于相關系數不足及區分度不高,判定為未在數據庫中找到識別類一類,即需要在擴充的數據庫中進行再識別。本算例驗證了HFS統計相關系數在處理多源異類數據識別問題的有效性,并且HFS統計相關系數計算時不需要對應屬性的HFE隸屬度個數相同,解決了傳統方法需要補齊隸屬度再計算相關系數的問題,因而相比傳統方法具有更好的計算精度。 針對多源異類數據的融合識別問題,基于猶豫模糊集框架,由猶豫模糊數、直覺模糊數、區間數和實數4類基本數據組成的多源異類數據,由猶豫模糊數統一描述,提出了HFS統計相關系數進行融合識別判定。首先分析了現有HFS統計相關系數的局限性,主要表現為定義違背統計學直覺、數學概念不明確、計算需要HFE中隸屬度個數相同和取值局限于[0,1]內等。為解決上述問題,提出HFS統計相關系數,使其既滿足統計學直覺,又不需要各HFE中隸屬度個數相同,并具有更強的數學概念。考慮實際問題中屬性權重的影響,將其拓展為加權HFS相關系數。最后利用所提出的HFS統計相關系數解決多源異類數據的融合識別問題。仿真算例對比分析并驗證了HFS統計相關系數的有效性,具有精度高、區分度好的優點。 從猶豫模糊的角度,為多源異類數據的融合識別問題提供了可行方法,具有現實意義。所提出的HFS統計相關系數計算方法可以拓展到區間猶豫模糊集、二重模糊集和猶豫語義標簽領域相關系數的計算中,以進一步地研究及應用。 [1] BUCCI D J. Assessing the performance of data fusion algorithms using human response models[J].Dissertations & Theses-Gradworks,2015. [2] ZADEH L A.Fuzzy sets[J].Information & Control,1965,8(3): 338-353. [3] SUN G D, GUAN X. Research on hybrid multi-attribute decision-making[C]∥Proc.of the International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, 2016: 272-277. [4] ZHANG X, XU Z, WANG H. Heterogeneous multiple criteria group decision making with incomplete weight information: a deviation modeling approach[J]. Information Fusion, 2015, 25: 49-62. [5] WAN S P, DONG J Y. Interval-valued intuitionistic fuzzy mathematical programming method for hybrid multi-criteria group decision making with interval-valued intuitionistic fuzzy truth degrees[J]. Information Fusion, 2015, 26(C): 49-65. [6] XU J, WAN S P, DONG J Y. Aggregating decision information into Atanassov’s intuitionistic fuzzy numbers for heterogeneous multi-attribute group decision making[J]. Applied Soft Computing, 2016, 41: 331-351. [7] WAN S P, LI D F. Atanassov’s intuitionistic fuzzy programming method for heterogeneous multi-attribute group decision making with Atanassov’s intuitionistic fuzzy truth degrees[J]. IEEE Trans.on Fuzzy Systems, 2014, 22(2): 300-312. [8] TORRA V. Hesitant fuzzy sets[J].International Journal of Intelligent Systems, 2010, 25(6): 529-539. [9] TORRA V, NARUKAWA Y. On hesitant fuzzy sets and decision[C]∥Proc.of the 18th IEEE International Conference on Fuzzy Systems, 2009: 1378-1382. [10] XU Z S, XIA M M. On distance and correlation measures of hesitant fuzzy inforrnation[J]. International Journal of Intelligent Systems, 2011, 26: 410-425. [11] CHEN N, XU Z S, XIA M M. Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis[J]. Applied Mathematical Modeling, 2013, 37(4): 2197-2211. [12] LIAO H C, XU Z S, ZENG X J. Novel correlation coefficients between hesitant fuzzy sets and their application in decision making[J].Knowledge-Based Systems,2015,82(C):115-127. [13] EBRAHIMPOUR M K, EFTEKHARI M. Feature subset selection using information energy and correlation coefficients of hesitant fuzzy sets[C]∥Proc.of the 7th International Conference on Information and Knowledge Technology, 2015: 1-6. [14] MENG F Y, CHEN X H, ZHANG Q. Correlation coefficients of interval-valued hesitant fuzzy sets and their application based on the Shapley function[J]. International Journal of Intelligent Systems, 2016, 31(1): 17-43. [15] WANG L, NI M F, ZHU L. Correlation measures of dual hesitant fuzzy sets[J]. Journal of Applied Mathematics, Volume 2013, 2013(4):1-12 [16] YE J. Correlation coefficient of dual hesitant fuzzy sets and its application to multiple attribute decision making[J]. Applied Mathematical Modeling, 2014, 38(2): 659-666. [17] TYAGI S K. Correlation coefficient of dual hesitant fuzzy sets and its applications[J]. Applied Mathematical Modeling, 2015, 39(22): 7082-7092. [18] FARHADINIA B. Correlation for dual hesitant fuzzy sets and dual interval-valued hesitant fuzzy sets[J]. International Journal of Intelligent Systems, 2014, 29(2): 184-205. [19] LIAO H C, XU Z S, ZENG X J, et al. Qualitative decision making with correlation coefficients of hesitant fuzzy linguistic term sets[J].Knowledge-Based Systems, 2015,76(1):127-138. [20] XU Z S, XIA M M. Distance and similarity measures for hesitant fuzzy sets[J].Information Sciences,2011,181(11): 2128-2138. [21] LIAO H C, XU Z S. Hesitant fuzzy decision making methodologies and applications[M]. Singapore Springer, 2017: 1-34. [22] XU Z S, ZHANG X L. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information[J]. Knowledge-Based Systems, 2013, 52(6): 53-64. [23] XIA M M, XU Z S. Hesitant fuzzy information aggregation in decision making[J]. International Journal of Approximate Reasoning, 2011, 52(3): 395-407. [24] LIAO H C, XU Z S, XIA M M. Multiplicative consistency of hesitant fuzzy preference relation and its application in group decision making[J]. International Journal of Information Technology and Decision Making, 2014, 13(1): 47-76.2 多源異類數據分析
3 猶豫模糊集統計相關系數
3.1 HFS的數學概念
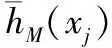
3.2 HFS統計相關系數

3.3 加權相關系數
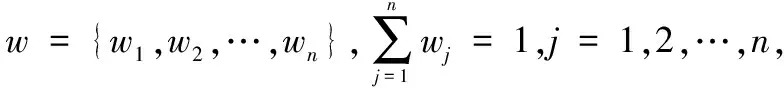
4 基于HFS統計相關系數的多源異類數據融合識別
4.1 多源異類數據的猶豫模糊表示
4.2 基于HFS統計相關系數的識別判定
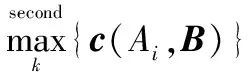

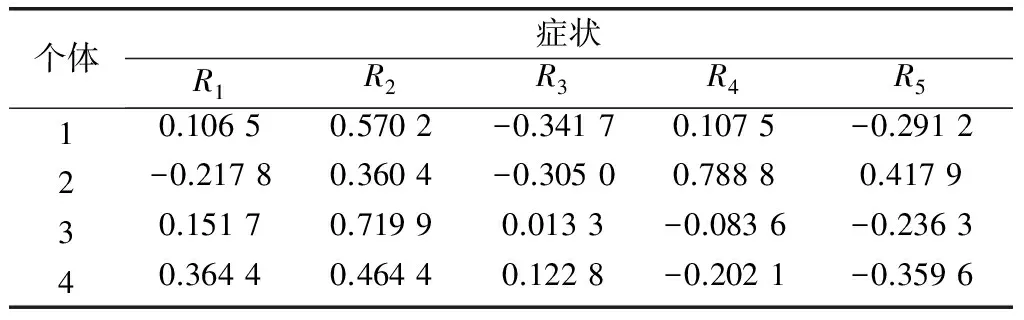
5 多源異類數據融合識別
5.1 算例1


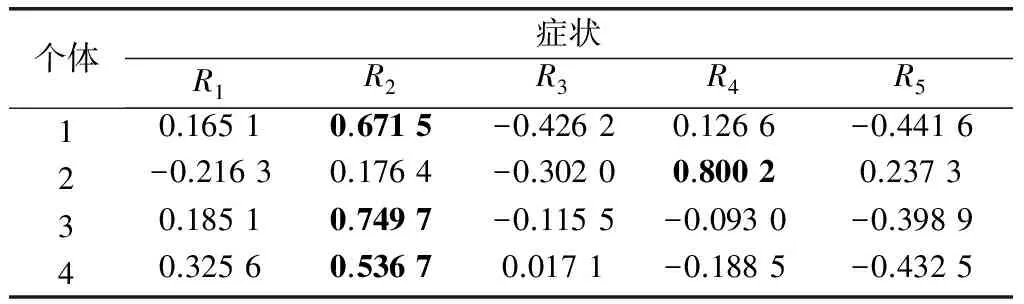
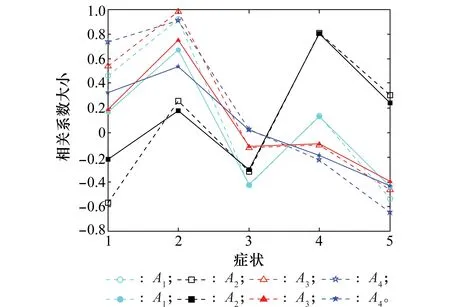
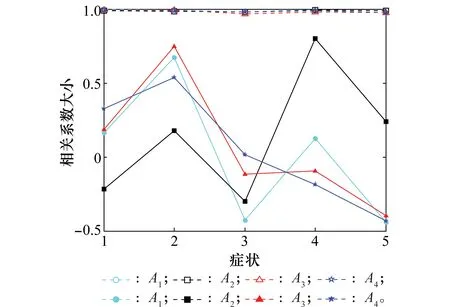

5.2 算例2
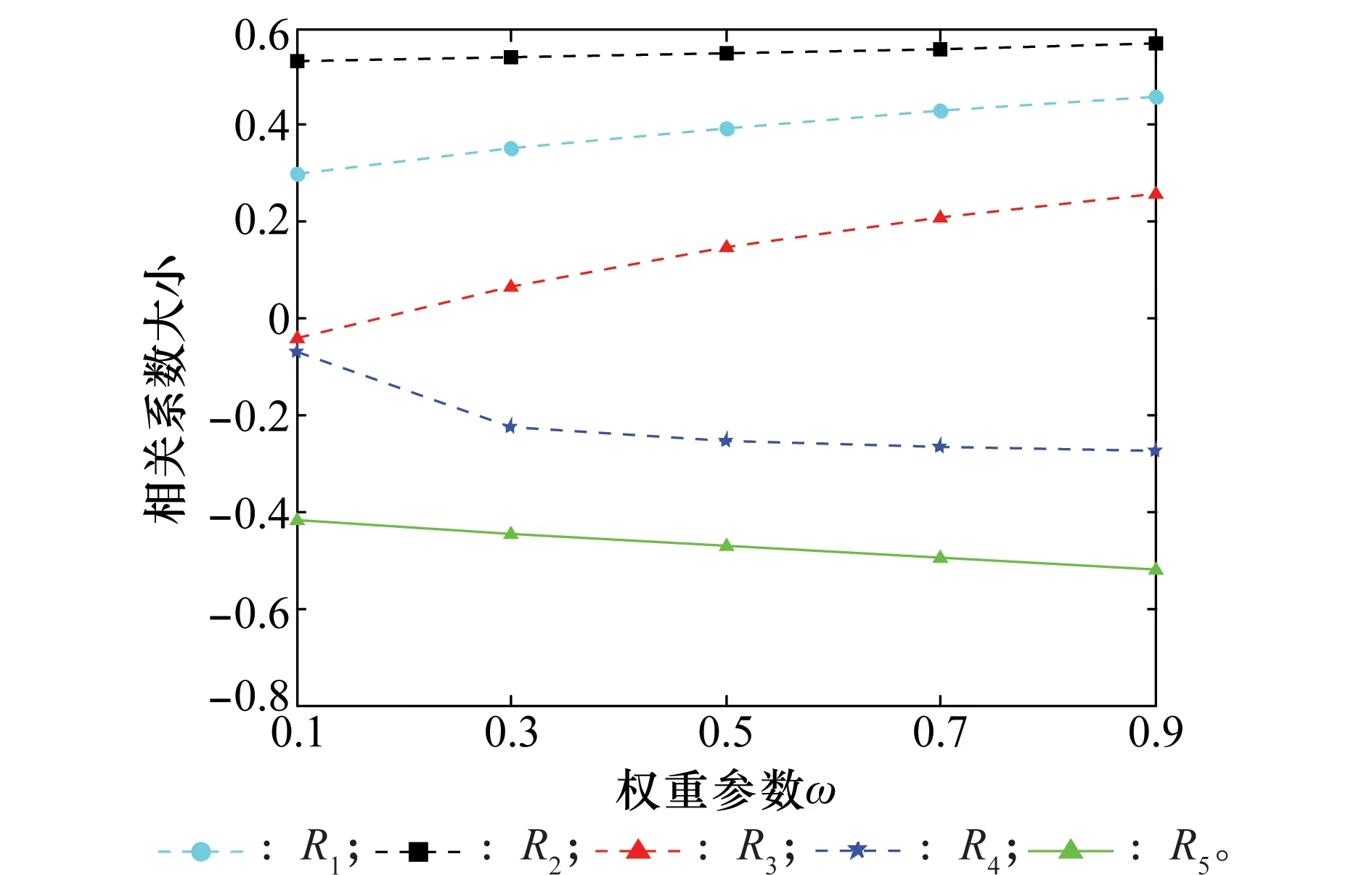
5.3 算例3
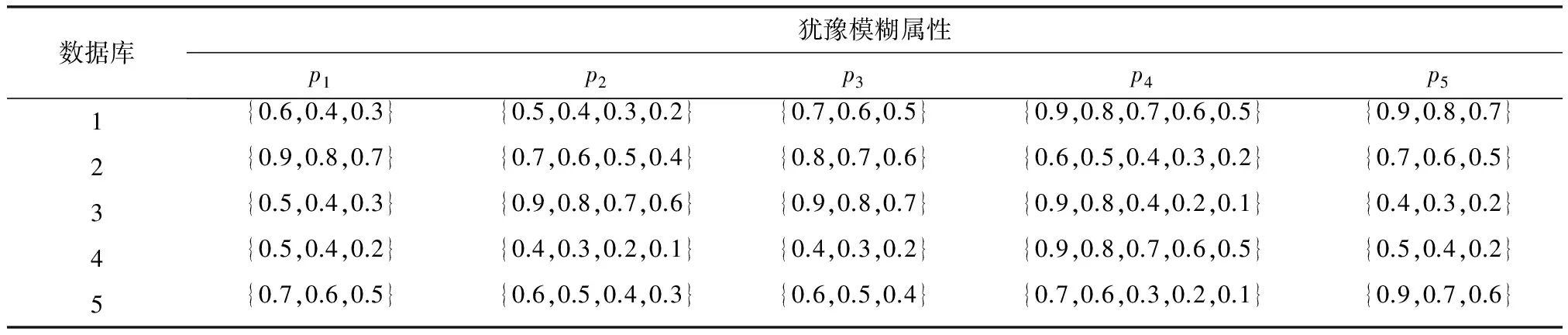


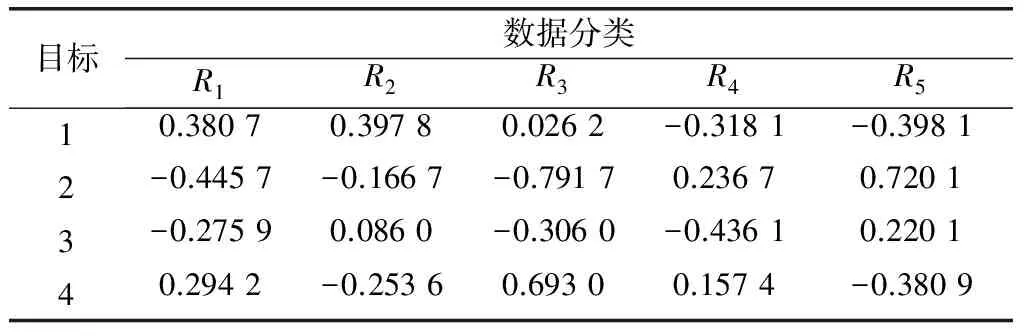
6 結 論

