面向不確定殘缺數據的大學生成績預測方法

曹歆雨+曹衛權+李崢+孫金德

摘 要： 大學生在課程規劃方面有很高的自由度，這使得成績數據較不規整，研究者很難對學生的前序課程成績進行有效分析、利用。已有的成績預測方法普遍未考慮學生前序課程成績殘缺的現象，從而導致預測準確性不佳。提出一種基于K近鄰局部最優重建的殘缺數據插補方法，該方法能夠有效抑制前序課程成績缺失對預測模型精度的影響。實驗表明，該方法的補全效果優于已有的均值插補、GMM插補等方法，結合隨機森林模型實現了有效的成績預測，為學生成績管理、就業能力預警提供了客觀的參考。

關鍵詞： 成績預測； 缺失數據； 數據插補； 數據挖掘； 機器學習； 隨機森林模型

中圖分類號： TN911?34； TP391 文獻標識碼： A 文章編號： 1004?373X（2018）06?0145?05

Abstract： College students have high freedom on their course planning， which makes the score data irregular and in disorder， and makes it difficult for researchers to effectively analyze and utilize students′ scores of foreword curriculums. The score missing phenomenon of students′ foreword curriculums is generally not considered in the existing score prediction methods， resulting in relatively low prediction accuracy. Therefore， a missing data imputation method based on local optimal reconstruction of k?nearest neighbors is proposed， which could effectively suppress the influence of foreword curriculum score missing on the accuracy of prediction model. The experimental results show that the completion effect of the proposed method outperforms that of the existing mean imputation method， GMM imputation method， and other methods. Effective score prediction is realized by combining with random forest model to provide an objective reference for students′ score management and early warning on students′ employability.

Keywords： score prediction； missing data； data imputation； data mining； machine learning； random forest model

0 引 言

高等教育問題是多年以來的社會熱點，從“精英教育”到“大眾教育”，高校擴大招生規模，面臨著學生質量參差不齊，就業形勢嚴峻等問題。如何準確評估大學生的學業完成質量，并進一步實現學業退步預警、就業質量預測等應用，逐漸受到數據分析研究者的關注[1?4]。學生成績不僅是評估高校教學質量的重要指標，還與學生管理及就業指導密切相關。有效預測學生成績并及時進行干預，可以為學生學習思想動態的引導和就業能力的評估提供重要的依據。

權小娟等基于985高校大學生的成績數據，分析了大學生成績的變化趨勢及城鄉差異[1]，分析結果具有一定的現實參考價值。但該文獻屬于描述性研究，僅分析了大學生群體成績發展規律，但并未給出有效的成績預測模型，故無法應用于大學生個體的成績預測、預警。

龍鈞宇等人提出基于頻繁模式發掘大學科目之間的強關聯關系，并預測學生未來若干課程的成績[2]。該方法有兩方面的局限性：首先，強模式關聯方法決定了一門課程的成績僅由當前的少數幾門成績甚至一門成績確定，限制了其預測準確率的提升空間；其次，該預測方法將成績分為4個等級，無法對成績進行精準、量化預測。

陳勇將遺傳神經網絡應用于大學生成績分析[3]，實現了精確的分值預測，并引入遺傳算法來解決BP神經網絡收斂速度慢、訓練時間長的問題。然而該方法的實驗并不完備，僅在16條成績數據上開展神經網絡訓練與預測，實驗結果不具統計可信性，也沒有足夠豐富的實證分析來佐證其模型方法的推廣能力。

已有的相關研究重點集中在學生群體成績預測、個體成績基本趨勢分析等方面，面向學生個體成績的精確預測研究相對較少。學生先后所學課程間存在潛在關聯性[2]，但隨著高校教育寬口徑、多樣化理念的深入，學生的學習課程種類繁多且存在較大自主選擇空間，專業課選修等進一步加大了學生所修課程的不確定性，很難保證同一專業所有學生均選修特定課程。此外，學生調整專業、缺考緩考等行為導致前序課程數據的缺失，給基于機器學習的成績預測方法帶來了極大的挑戰。已有研究工作中往往沒有考慮這一因素[3]。當學生并未取得預測系統所關心的強關聯性課程成績時，將這種情況稱為數據殘缺。如何在學生成績數據存在不確定性殘缺的情況下，仍能基于已有的部分科目成績，推測其未來學業走勢，是本文的主要研究內容。endprint

針對隨機殘缺數據，根據模型的精細程度，存在均值插補（Mean Imputation Method，MEI）[5]、GMM插補[6]、CMeans插補[7]等方法。本文提出一種基于KNN局部最優重建的插補方法，并對比了不同插補方法對成績預測問題的增益，實驗表明，該方法相比于已有插補方法更優，能夠有效解決大學生自由選課情況下的成績預測問題。

1 數據預處理與問題分析

1.1 學生專業與主修課程

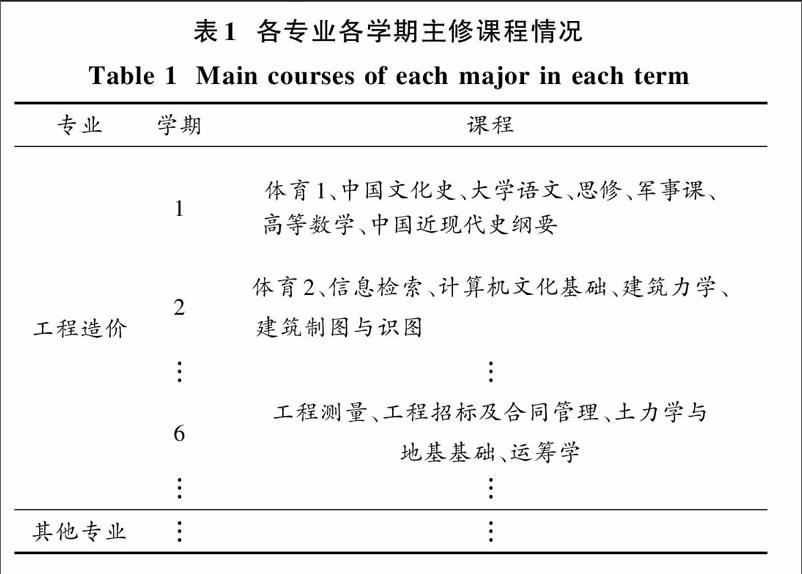
本文以四川師范大學2009—2012級共4屆本科生的全部成績數據為基礎，分析問題并驗證所提出方法的有效性。基于學生選課情況，按照選課人數比率，統計出各專業在每一學期的熱門課程，如表1所示。

在本文后續分析中，出于訓練效率和“過學習”問題的考慮，針對任一學生，將只考慮其所在專業、對應學期的熱門課程成績，而不考慮其他冷門課程的成績。

1.2 分學期成績預測及其可靠性

針對任一熱門課程[c]及其所在學期[pc]、專業[mc]，預測該課程成績的輸入特征變量包括如下課程集合對應的成績：

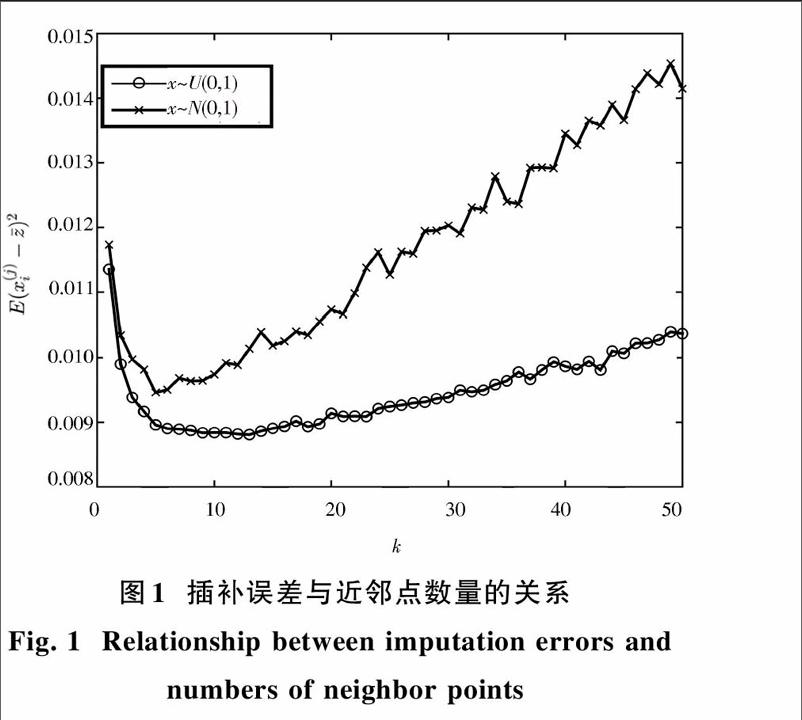
[Ic=c′pc′

根據已有成績數據和式（1）所示的預測規則，構建了大量的回歸型（以區別于分類型）機器學習任務[T] ，每項學習任務的目標變量[y] 即學生在各學期熱門課程[c] 的成績[sc]，輸入變量[xn×1]為該學生在課程集合[Ic]中取得的成績。對于某學生未選修課程[c′∈Ic]的情況，則設置對應的字段[sc′]為缺失項。

基于隨機森林算法[8]，對上述各學習任務進行訓練、預測，得出各機器學習任務的均方根誤差（Root Mean Squre Error，RMSE）。對所有RMSE估計一維概率密度[9]，得出RMSE的分布。

考慮到不同課程成績的分散程度不同，需采用式（2）計算各課程成績預測結果的相對均方根誤差，該數值越小表明預測效果越好。

[RRMSET=RMSETVarsc] （2）

定義1 根據[RRMSE] 指標對所有的課程成績預測任務進行排序，選出[RRMSE] 最小的部分課程集合[Cr]，稱為可預測課程。

基于學生已有的成績數據來預測[c∈Cr] 是有意義的；反之，預測[c′?Cr] 的誤差較大，不具參考價值。

1.3 數據殘缺問題

第1.2節測試得出的部分可預測課程及其數據缺失情況如表2所示。其中，對于可預測課程[c]，若其前序熱門課程[Ic]至少有一項無成績，則記錄該樣本為殘缺樣本。

由于其前序課程[Ic] 數量較多，因此對成績預測系統而言，數據缺失是普遍存在的現象，且數據集的殘缺情況相當嚴重，缺失率普遍高達40%～50%。

2 數據插補與成績預測

K近鄰法（KNN）是一種更有效數據插補方法[10]：該方法對于殘缺樣本[xi]，基于其已知的部分分量[Ac]尋找[xi]在完整樣本集[Xc]中的KNN，然后利用k個近鄰點的均值或眾數來填充[xi]的未知字段[Am]。

2.1 KNN插補誤差分析

首先考慮[xi]僅包含一維未知分量[xji]的情況。假定可以尋找到[xji]的K近鄰（實際上[xji]在未知的情況下是無法搜索K近鄰的），基于k個近鄰點的均值來插補[xji]。設[xj?U0，1]，考慮完整樣本集[Xc] 的元素獨立同分布，則其第[m]個近鄰點與[xji]差值[zm=xjm-xji]的概率密度函數為：

[gmz=1Bm，N-m+1?1-Fz+F-zm-1? Fz-F-zN-mfz] （3）

式中：[F?]，[f?] 分別為隨機變量[xj-xji] 的概率分布函數和概率密度函數；[B?] 為Beta函數，如下：

[Bα，β=ΓαΓβΓα+β=α-1！β-1！α+β-1！] （4）

根據[gmz]可以求得利用KNN估計[xji]的均值偏移[Ezxji；k]以及方差[Varzxji；k]，進而利用式（5）、式（6）得出KNN插補的總體均偏與方差。一般地，[k] 越小則[Varz；k]越小，插補效果越好。

[Ez；k=EEzxji；k] （5）

[Ez2；k=EEz2xji；k] （6）

通過蒙特卡洛法[11]仿真不同分布函數下KNN插補殘差，如圖1所示。

注意到，在[xj]服從不同概率分布時，KNN插補殘差隨著k值的增加總是呈現先降低后升高的趨勢。在k較小時，模型誤差[ε]主導插補殘差；在k較大時，則由較遠的[zk，zk-1，…] 主導殘差。KNN插補方法[10]簡單地指定恒定的參數k，而未討論如何選擇最優的k值使得插補殘差最小。

2.2 基于KNN局部線性重建的插補方法

針對待插補樣本[xi]，假設已經基于其已知分量[Ac] 獲取了k個近鄰點，并將這些近鄰點按列拼接為矩陣[Pd×k]，其中[d]為已知分量的維數。為了解決最優k值未知的問題，借鑒Kang等的最優重建思想[10]，通過求解式（7）所示的凸優化問題，賦予各近鄰點最優權重[wk×1]。

[minwfw=12Pw-xAci2s.t. w0， w=1] （7）

上述優化問題可以利用序列最小優化（Sequential Minimal Optimization，SMO）實現快速求解。設優化問題的對偶變量為[αk×1]和[β1×1]，分別對應不等式約束和等式約束，則該問題對應的Lagrange函數為：

[Lw，α，β=12Pw-xAci2-αTw-β1Tws.t. α0] （8）

對應的KKT條件為：

[?L?w=PTPw-PTx-α-1?β=0] （9）

[1Tw=0] （10）

[αiwi=0， i=1，2，…，k] （11）

采用數值解法，求得滿足式（9）～式（11）所定義KKT條件的解即為式（7）的最優解。

圖1 插補誤差與近鄰點數量的關系

Fig. 1 Relationship between imputation errors and

numbers of neighbor points

在本小節描述的算法中，對任意變量[v]，[vm]表示該變量第[m]輪迭代的取值，[vi]表示向量的第[i]個元素，[vi→]，[vi↓]分別表示矩陣的第[i]個行、列向量。

利用SMO算法的思想，一次迭代僅優化[w]的兩維分量，同時結合式（9）～式（11）的KKT條件，設計最優權重的快速求解算法，具體步驟如下。

1） 查詢任一破壞式（9）～式（11）KKT條件的分量[wi]，并隨機選取另一分量[wj]，若未找到[wi]則優化終止；

2） 限制[wm+1i+wm+1j=wmi+wmj=C]，限制其他[wm+1l≠i，j]保持不變；

3） 采用解析法優化函數[fwm+1i]；

4） 將最優解[wm+1i]限制在區間[0， C]；

5） 更新[w]，[β]，[α]等，進入下一輪迭代。

為了保證上述算法可復現，需要分別在步驟1）明確如何確定破壞KKT條件的[wi]，在步驟3）明確如何優化函數[fwm+1i]，在步驟5）明確如何更新[β]與[α]。

在定義的KKT條件中，式（9）通過步驟5）強制滿足，式（10）通過步驟2）強制滿足，因此在步驟1）中，可以通過僅檢查[αiwi>ε]來確定[wi]。其中[ε]為極小量，如[10-6]，使得算法穩定。

當按照步驟2）約束[wj]及其他分量時，目標函數簡化為式（12）定義的一維二次函數，式中的[?]為常向量，在每次迭代時更新。

[2fw=l=1kPl↓wl-xAci2=Pi↓-Pj↓wi+?2] （12）

無約束條件下，最小化上述一維函數，可得步驟3）的最優[wi]，如下：

[w*i=-Pi↓-Pj↓-2Pi↓-Pj↓T?] （13）

最后，按照式（9）～式（11）的KKT條件更新[α]和[β]。采用上述解法有兩項顯著優點：一是求解速度更快；二是當[P]非列滿秩，回避內點法的矩陣奇異問題。

2.3 成績預測流程

結合本文第2.2節的數據插補方法，提出圖2所示的成績預測流程。

3 實證分析

3.1 數據準備與評估準則

本節以四川師范大學2009—2012級共4屆本科生的成績數據，驗證所提出方法的有效性。參照第1.2節的做法，根據學生專業、選課情況、非插補條件下成績先驗預測結果，選出各專業學生對應的共17項可預測課程，其中部分可預測課程已在表2中列出。以待預測課程為因變量、以該課程對應的前序課程為自變量、以課程對應專業全體學生為樣本集合，最終構成多項成績預測任務。

針對每項預測任務，分別采用MEI插補[5]、GMM插補[6]、CMeans插補[7]、和本文方法對數據進行補全，并采用多種機器學習方法預測目標課程成績，取各種機器學習方法預測RMSE的平均值作為數據插補方法的性能評估準則。本節采用的機器學習方法包括IBK、決策表、線性回歸、M5P、隨機森林等預測模型，每種數據插補方法和預測模型分別重復試驗30次，并取均值作為性能度量，以保證實驗結果的統計可信性。

3.2 插補效果對比

對比不同插補方法對學生成績缺失狀況的插補效果，如圖3所示。其中，缺失率從0%～50%不等。

注意到，若直接舍棄含缺失項的樣本，隨著缺失率的增加，RMSE指標呈線性增長。對比不同的數據插補策略，本文提出的KNN插補方法能夠在多項成績預測任務中取得最佳的補全效果，較好地解決了學生成績數據中普遍存在的不確定殘缺問題。

3.3 機器學習算法對比

基于第3.1節的實驗設置，對比不同預測模型的預測精度，結果如圖4所示，其中所有預測模型默認采用本文KNN插補方法對成績數據進行了補全。

對比圖4發現，隨機森林模型相比于其他預測模型精度更高。同時，得益于精準的數據插補方法，隨機森林模型的預測誤差隨缺失率增長緩慢，結合兩種方法預測學生成績是一種可行的技術思路。

4 結 語

本文針對高校學生成績預測預警問題，分析了不同課程間的關聯強度。由于學生選課自由度較高，學生部分前序課程普遍面臨著成績缺失的現象。針對這一問題提出了基于KNN局部線性重建的插補方法來補全原始數據，該方法解決了KNN參數選擇的問題，具有較好的穩定性。實驗結果表明，結合本文的KNN插補策略和隨機森林模型，能夠實現高校學生未來成績的準確預測，為基于數據驅動的現代化學生管理提供可靠的參考。

參考文獻

[1] 權小娟，朱曉文.大學生學習成績變化趨勢及其影響因素的實證研究[J].復旦教育論壇，2016，14（5）：45?51.

QUAN Xiaojuan， ZHU Xiaowen. The changing trend in college students academic achievement and its influential factors： an empirical analysis [J]. Fudan education forum， 2016， 14（5）： 45?51.

[2] 龍鈞宇.基于壓縮矩陣Apriori算法的高校學生成績相關性分析研究[J].現代電子技術，2014，37（24）：47?51.

LONG Junyu. Research on correlation analysis of college student′s achievements based on Apriori algorithm with compressed matrix [J]. Modern electronics technique， 2014， 37（24）： 47?51.

[3] 陳勇.基于遺傳神經網絡成績預測的研究與實現[J].現代電子技術，2016，39（5）：96?100.

CHEN Yong. Research and implementation of result prediction based on genetic neural network [J]. Modern electronics technique， 2016， 39（5）： 96?100.

[4] 葉苗.大數據分析大學生就業率估計模型仿真[J].計算機仿真，2016，33（11）：183?186.

YE Miao. Big data analysis of college students′ employment rate estimation model simulation [J]. Computer simulation， 2016， 33（11）： 183?186.

[5] LEE T， CAI L. Alternative multiple imputation inference for mean and covariance structure modeling [J]. Journal of educational & behavioral statistics， 2012， 37（6）： 675?702.

[6] YAN Xiaobo， XIONG Weiqing， HU Liang， et al. Missing value imputation based on Gaussian mixture model for the Internet of Things [J]. Mathematical problems in engineering， 2015（3）： 1?8.

[7] TANG J， ZHANG G， WANG Y， et al. A hybrid approach to integrate fuzzy C?means based imputation method with genetic algorithm for missing traffic volume data estimation [J]. Transportation research part C： emerging technologies， 2015， 51（1）： 29?40.

[8] BREIMAN L. Random forests [J]. Machine learning， 2011， 45（1）： 5?32.

[9] NAGLER T， CZADO C. Evading the curse of dimensionality in multivariate kernel density estimation with simplified vines [J/OL]. [2018?01?27]. https：//arxiv.org/pdf/1503.03305v1.pdf.

[10] KANG P. Locally linear reconstruction based missing value imputation for supervised learning [J]. Neurocomputing， 2013， 118（11）： 65?78.

[11] JANSSEN H. Monte?carlo based uncertainty analysis： sampling efficiency and sampling convergence [J]. Reliability engineering & system safety， 2013， 109（2）： 123?132.

[12] WITTEN I H， FRANK E， HALL M A. Data mining： practical machine learning tools and techniques [M]. Beijing： China Machine Press， 2005.endprint