EQ－代數(shù)的模糊濾子粗糙性研究

段喆杰

(渭南師范學(xué)院絲綢之路藝術(shù)學(xué)院，陜西渭南714099)

1 ΕQ－代數(shù)的相關(guān)定義

定義 1［1－2］一個(2，2，2，0) 型代數(shù) Ε =〈E，∧，，～，1〉，如果滿足:

(1)〈E，∧，1〉有最大元1且是一個∧半格，如果 a∧b=a，記a≤b;

(3)a～a=1;

(6)(a∧b∧c)～a≤(a∧b)～a;

則稱Ε是一個ΕQ－代數(shù)。

定理 1［1－2］在 ΕQ－代數(shù) Ε 中以下結(jié)果成立:對任意的 a，b，c∈E，有

(2)a=b當(dāng)且僅當(dāng)a～b=1;

(4)a→b=(a∧b)～a;

(5)a～b≤a→b和a→a=1;

(7)若 a≤ b，則a→b=1，a ～ b=b→a，c→ a≤ c→ b，b→c≤a→c;

(8)b≤ b～≤ a → b。

定理2［2］設(shè)Ε是一個ΕQ－代數(shù)，下列性質(zhì)在Ε中成立:

(1)a～b=b～a;

(3)a～b≤(a～c)～(b～c)。

定義2［2］設(shè)Ε是一個ΕQ－代數(shù)，若

(1)對任意的a，b∈E，由a～1=1推出a=1，則稱Ε為半可分的。

(2)對任意的a，b∈E，由a～b=1推出a=b，則稱Ε為可分的。

定義 3［2］設(shè) Ε=〈E，∧，，～，1〉是一個可分的 ΕQ－代數(shù)，F(xiàn)≤E，如果對任意的 a，b∈E，

(1)1∈F;

(2) 如果對a，a→b∈F，則b∈F，則F就稱為E的準(zhǔn)濾子。

定理3［2］設(shè)F是一個可分ΕQ－代數(shù)E的準(zhǔn)濾子，且a～b∈F，a'～b'∈F，則下列式子成立:

(1)(a ∧a')～ ( b ∧b')∈F;

(2)( a ～a')～ ( b ～b')∈F;

(3)( a →a')～ ( b →b')∈ F。

定理4［2］設(shè)F是可分的ΕQ－代數(shù)E的一個準(zhǔn)濾子，對任意的a，b∈E，如果a～b∈F，b～c∈F，則a～c∈F。

定理5［3］設(shè)E是一個可分的ΕQ－代數(shù)，F(xiàn)是E的濾子。則≈是E上的一個同余關(guān)系。

我們把 [a ]F記為a∈F關(guān)于≈F的等價類。

定義4［3］設(shè)E是一個可分的ΕQ－代數(shù)，F(xiàn)是E上的準(zhǔn)濾子。定義E上一個二元關(guān)系“≈”如下:

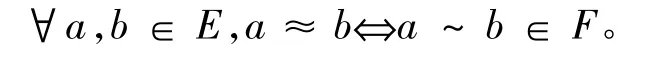
定理6［3］設(shè)E是一個可分的ΕQ－代數(shù)，F(xiàn)是E的濾子，則:

(1)［x］F=［y］F;

(2)x=y ～ h，-h∈ F。

定義5［3］設(shè)E是一個可分的ΕQ－代數(shù)，X是E的子集。如果x，y∈X，z∈E且x≤z≤y，若能推出z∈X，則稱X是凸的。

定理7［3］設(shè)F是可分的ΕQ－代數(shù)E的濾子，則對每一個a∈E，[a]是凸的。

F

定理8［3］設(shè)F是一個可分的ΕQ－代數(shù)E上的濾子并且E是線性序的，如果x≤y且［x］ ≠［y］，

FF則對 t∈［x］F，s∈［y］F，有 t≤ s。

定義6［4－5］設(shè)(U，θ)是一個近似空間，Apr:P(U)→ P(U) ×P(U)，對任意的 X∈ P(U)，定義，稱其為(U，θ)上X的上近似空間;若，稱其為(U，θ)上X的下近似空間。并稱θ)上X的粗糙近似空間。

設(shè)(U，θ)是一個近似空間，X是U的一個非空子集。

在一個近似空間(U，θ)上，φ和U關(guān)于θ可定義是顯然的。所以以Def(Apr)被記為所有可定義的集合。

2 可分ΕQ－代數(shù)的模糊準(zhǔn)濾子

(1)A(1)≥A(x)，對任意的x∈E;

如果對任意的 a，b，c∈ E，有

則模糊準(zhǔn)濾子稱模糊濾子。

如果對所有a，b∈E有A(a→b)=1或A(b→a)=1，則模糊準(zhǔn)濾子也稱是素模糊準(zhǔn)濾子。……